【数据结构与算法 | 基础篇】力扣232, 225
1. 力扣232 : 用栈实现队列
(1). 题
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false]解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false
提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty - 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
(2). 思路
用两个栈模拟队列. 先设计两个栈,分别作输入栈,输出栈. 如果执行push操作,将元素压入输入栈. 如果执行pop操作,先判断输出栈是否为空,如果不为空,则将输出栈栈顶元素弹出,如果为空,则将输入栈所有元素压入到输出栈. peek操作同pop操作. empty判断队列是否为空,只需判断输入栈与输出栈是否同时为空. 如果同时为空,则return true.
(3). 解
class MyQueue {//声明输入栈, 输出栈private Deque<Integer> inStack;private Deque<Integer> outStack;public MyQueue() {inStack = new LinkedList<>();outStack = new LinkedList<>();}public void push(int x) {inStack.push(x);}public int pop() {//如果输出栈此时不为空, 则弹栈if(!outStack.isEmpty()) {return outStack.pop();}while(!inStack.isEmpty()){outStack.push(inStack.pop());}return outStack.pop();}public int peek() {if(!outStack.isEmpty()) {return outStack.peek();}while(!inStack.isEmpty()){outStack.push(inStack.pop());}return outStack.peek();}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty();}
}/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = new MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* boolean param_4 = obj.empty();*/2. 力扣225 : 用队列实现栈
(1). 题
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的标准操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false]解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
进阶:你能否仅用一个队列来实现栈。
(2). 思路
难崩,虽然题目说是让两个队列实现栈,但试着让栈实现栈,套个小马甲,没想到居然通过了.hhhh
(3). 解1
class MyStack {private Deque<Integer> satck;public MyStack() {satck = new LinkedList<>();}public void push(int x) {satck.push(x);}public int pop() {return satck.pop();}public int top() {return satck.peek();}public boolean empty() {return satck.isEmpty();}
}/*** Your MyStack object will be instantiated and called as such:* MyStack obj = new MyStack();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.top();* boolean param_4 = obj.empty();*/相关文章:

【数据结构与算法 | 基础篇】力扣232, 225
1. 力扣232 : 用栈实现队列 (1). 题 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移…...

内网(极空间)搭建gitlab跳板机转发端口及域名配置
背景说明 https://blog.csdn.net/GodDavide/article/details/139182475 上文说到: 我已经用docker搭好了gitlab-ce服务,但我是部署在自己的家庭nas-极空间z4pro里的,属于内网环境。 另外我有一台阿里云服务器,做跳板机。 我有一个阿里的域名…...

如何知道自己电脑的 Shell类型是什么?
在macOS中,你可以通过以下几种方法来确定当前正在使用的shell类型,并了解相关的配置文件: 1. 使用终端命令确定shell类型 打开终端应用程序(Terminal)。输入以下命令并按回车键:echo $SHELL。该命令会输出…...

Axios的使用简单说明
axios 请求方式和参数 axios 可以发送 ajax 请求,不同的方法可以发送不同的请求: axios.get:发送get请求 axios.post:发送post请求 axios.put:发送put请求 axios.delete:发送delete请求 无论哪种方法,第一…...

查找list集合中,持续时间>=ContinueTime的数据集合,保存在新的list中
在给定的包含时间戳的list中,查找连续continueNum次的且时间间隔为needDiff的集合。 eg:相邻两个数据的时间戳间隔为1分钟,且超过30分钟有数据 /**** param list 包含时间戳(10位)的list* param continueNum 至少持续…...

nginx 反向代理配置详解
Nginx 反向代理是一种常用的部署策略,用于将客户端请求转发到内部网络中的一个或多个服务器,这些服务器直接处理请求并返回响应给Nginx,再由Nginx转交给客户端。这种设置可以提高网站的可用性和安全性,同时也能实现负载均衡、缓存…...
微信小程序毕业设计-农场驿站平台系统项目开发实战(附源码+论文)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...

CAN总线应用协议CANopen
作为一种真正开放的CAN总线高层协议,CANopen协议允许不同的CAN设备以标准化的方式进行通讯,这使得CAN 设备具有互操作性。随着CANopen协议的日益完善,它已经广泛应用于多个行业。本文将对CANopen协议的对象字典、通讯对象、网络管理等几个方面…...

htop安装不了怎么解决
🌟🌌 欢迎来到知识与创意的殿堂 — 远见阁小民的世界!🚀 🌟🧭 在这里,我们一起探索技术的奥秘,一起在知识的海洋中遨游。 🌟🧭 在这里,每个错误都…...

vue 笔记02
目录 01 事件修饰符 02 按键修饰符 03 v-bind属性 04 vue-axios的基本使用 05 vue的生命周期 06 vue生命周期涉及到的其他的知识点 01 事件修饰符 vue的事件修饰符 事件名称.修饰符1.修饰符2...事件驱动函数 stop 阻止冒泡修饰符 prevent 阻止默认行为 once 当前事件只触…...

MySQL8.0免安装及phpmyadmin配置
安装包解压,运行mysqld文件后,启动net start,提示成功,但进入phpmyadmin登录页面后,输入用户名,提示不支持空密码,config.default.php设置密码后,提示 mysqli::real_connect(): (HY…...
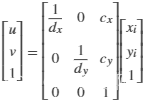
【目标解算】相机内外参数详细解读+坐标系转换
一、相机参数介绍 1.1 相机内参矩阵 概念:内参矩阵用于描述相机的内部参数,它包含了相机的焦距、主点坐标和图像的畸变等信息。内参矩阵的形式通常为一个3x3的矩阵,常用表示为K。内参矩阵可以将相机坐标系中的三维点映射到图像平面上的二维…...

【Unity】颜色混合计算
在图形渲染中,颜色混合(Color Blending)是指将多个颜色值组合在一起以生成最终显示的颜色。颜色混合技术广泛用于处理半透明效果、光照效果和后期处理效果。以下是一些常见的颜色混合模式: 1. 正常混合(Normal Blendi…...

Vue源码解析
入门级 <body><div id"app"></div><script>class Vue {constructor(options) {// thisVue 把options.created的this 指向Vue实例options.created.bind(this)();// this.$el 指向#appthis.$el document.querySelector(options.el);// 把opt…...
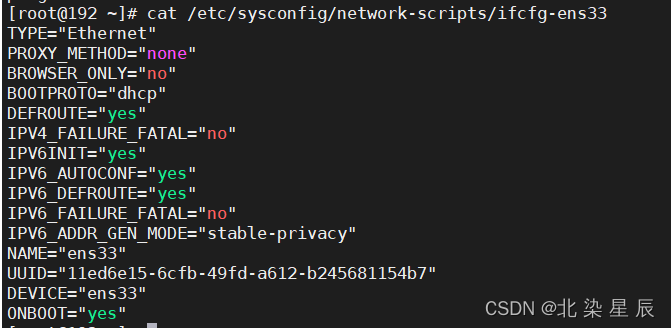
Linux---网络相关配置
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 一台主机需要配置必要的网络信息,才可以连接到互联网,需要的配置网络信息包括IP,子网掩码,网关和DNS。 一.查看网络信息 查看IP信息可以通…...
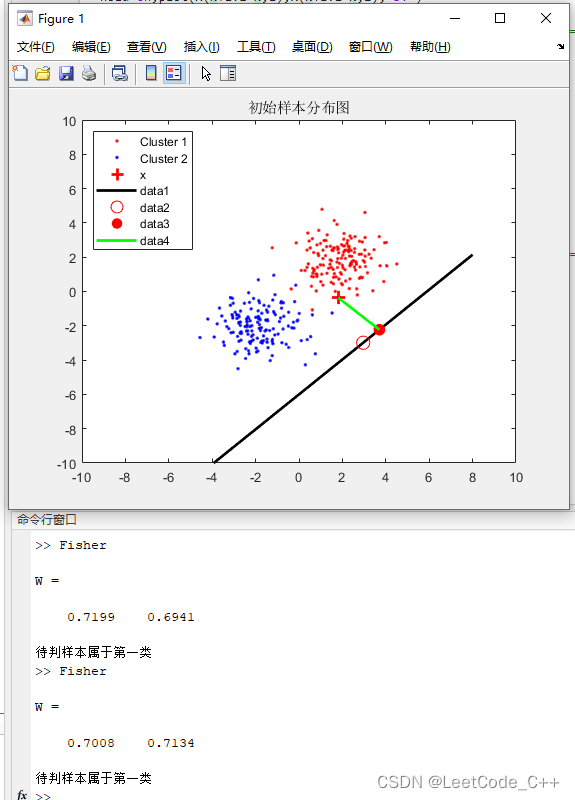
MATLAB分类与判别模型算法:基于Fisher算法的分类程序【含Matlab源码 MX_002期】
算法思路介绍: 费舍尔线性判别分析(Fishers Linear Discriminant Analysis,简称 LDA),用于将两个类别的数据点进行二分类。以下是代码的整体思路: 生成数据: 使用 randn 函数生成随机数&#x…...

长文总结 | Python基础知识点,建议收藏
测试基础-Python篇 基础① 变量名命名规则 - 遵循PEP8原则 普通变量:max_value 全局变量:MAX_VALUE 内部变量:_local_var 和关键字重名:class_ 函数名:bar_function 类名:FooClass 布尔类型的变量名…...

centos中使用Docker安装rabbitmq记录
一、安装rabbitmq docker run -d --name rabbitmq -p 5672:5672 -p15672:15672 -v rabbitmq-plugin:/plugins -e RABBITMQ_DEFAULT_USERxiaoqi -eRABBITMQ_DEFAULT_PASS123456 rabbitmq:latest二、配置web管理界面 # 查看运行的容器 docker ps -a # 根据容器id进入容器内部 …...

STM32系列-STM32介绍
🌈个人主页:羽晨同学 💫个人格言:“成为自己未来的主人~” STM32介绍 STM32介绍 ST:指的是意法半导体 M:指定微处理器 32:表示计算机处理器位数 ARM分成三个系列: Cortex-A࿱…...

网络原理 一
一、协议 网络通信中,协议是非常重要的概念. 协议进行了分层,此处就是按照这几层顺序来介绍每一层中的核心协议. 应用层,就对应着应用程序,是程序员打交道最多的一层,调用系统提供的 网络api 写出的代码都是基于应用层的. 应用层这里当然也有很多现成的协议,但更多的还是,程…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
