【数据结构:排序算法】堆排序(图文详解)
🎁个人主页:我们的五年
🔍系列专栏:数据结构课程学习
🎉欢迎大家点赞👍评论📝收藏⭐文章


目录
🍩1.大堆和小堆
🍩2.向上调整算法建堆和向下调整算法建堆:
🍟向上调整算法:
🍟向下调整算法:
🍟用这两种方法建堆的时间复杂度:
🍩3.堆排序:
🍩1.大堆和小堆
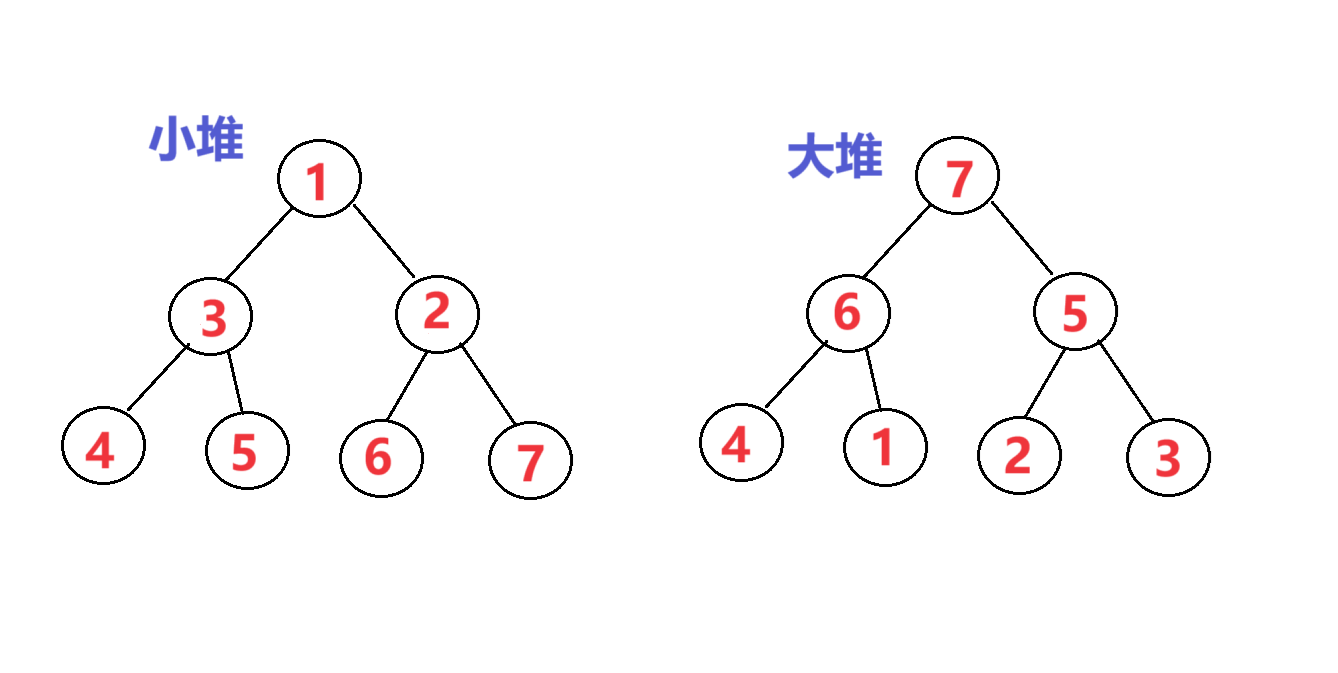
要想弄明白堆排序,我们先来看看大堆和小堆的概念和区别:
注意:堆是完全二叉树。
大堆:父节点都大于孩子节点。
小堆:父节点都小于孩子节点。
🍩2.向上调整算法建堆和向下调整算法建堆:
注:根节点我定为0
🍟向上调整算法:
向下调整算法调整该节点的前提是该节点以上的树已经是堆(大堆或者小堆),但是开始的时候,树里面的元素是随便放置的,但是可以把根元素以上看成一个堆,然后向上调整从2*0+1(第二层左边的元素)的位置开始就可以了。
以向上调整建立大堆为例:
从已经建好的堆的下一层开始向上调整,这里可以把根看成小堆,要想把整个二叉树调整为小堆形式,我们就要从根的下一层,把每个元素都进行一次向上调整。
向上调整的实现:
根该节点开始,我们把该节点与它的父节点进行比较,因为该节点以上的节点已经是大堆,此时的根是该树最大元素,所以只要和根比较谁大,如果比根大就交换位置,这样增加一个元素以后,该树还是大堆。
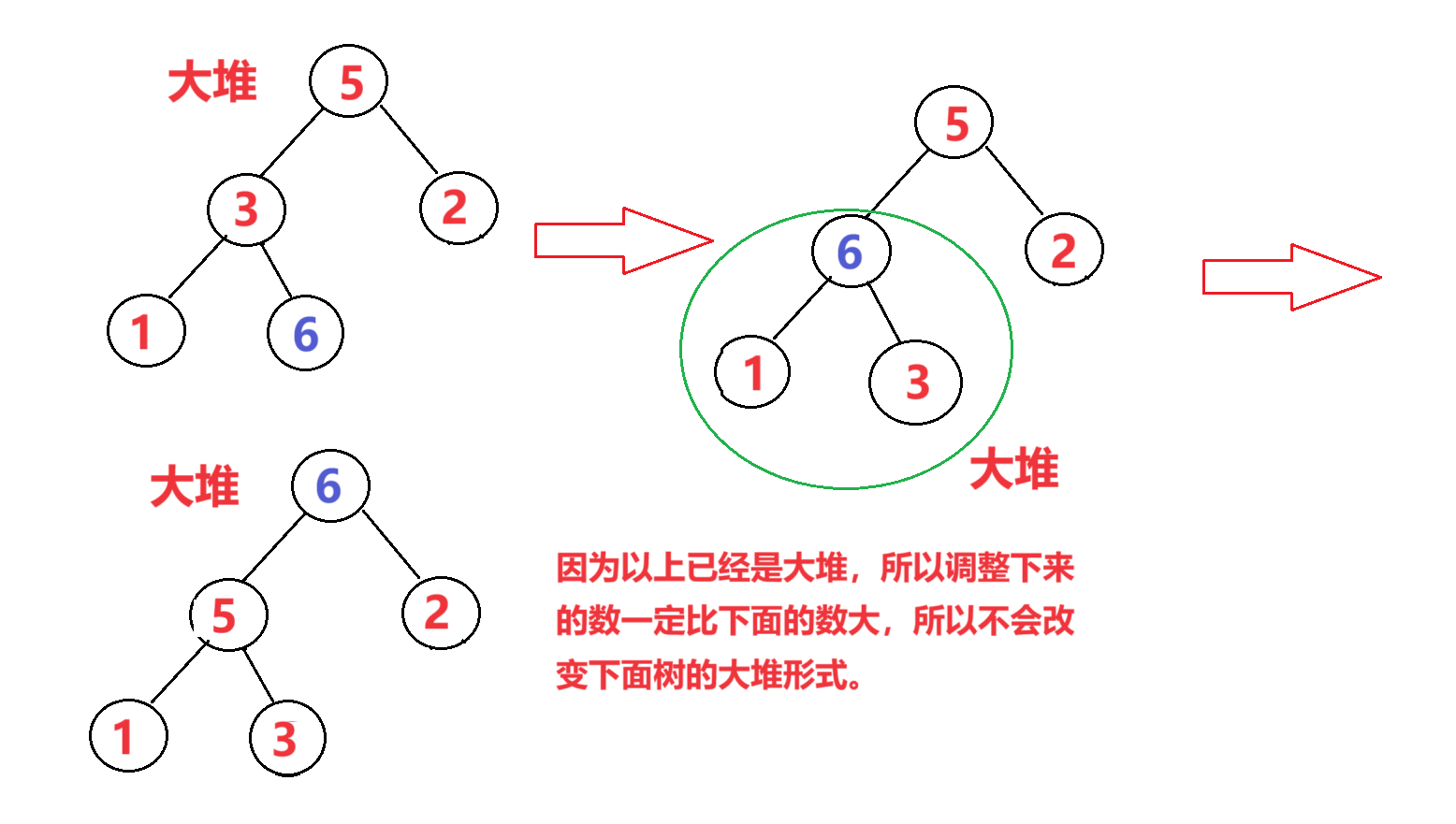
从上面图来看,向上调整结束的条件为该节点到达根节点,上面没有元素了。
由孩子节点的下标找到父节点的下标是:parent=(child-1)/2。
实现代码:
void AdjustUp(int* a,int child)
{//该节点开始比较int parent = (child - 1 - 1) / 2;while (child > 0) //当节点到达根节点,就没有父亲节点了,就停止{if (a[parent] < a[child]){int tmp = a[parent];a[parent] = a[child];a[child] = a[parent];child = parent;parent = (child - 1 - 1) / 2;}else{break;}}
}🍟向下调整算法:
向下调整算法的要求就是左右子树已经是堆(大堆或者小堆)。结束的条件是孩子节点为NULL。
代码为:
void AdjustDown(int* a, int size, int parent)
{//假设法int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1]>a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}🍟用这两种方法建堆的时间复杂度:
假如待排序的二叉树有K层,假设为满二叉树:
如果用向上调整算法,那么进行的次数是:第1层:2^0*0 //2的0次方这这一层的节点个数,0是调整的次数,根节点向上调整的时候 ,不需要调整。
第2层:2^1*1
……
第K层:2^(k-1)*k-1
所以总的次数为:
2^0*0+2^1*1+2^2*2+……+2^(k-1)*k=(k-1)*2^k-2.
个数N=2^k-1.k=log2 (N+1)
所以O(N)=(log2 (N+1)-1)*(N+1)-2。
数量级在log N
所以O(N)=N*log N。
向下调整:
其实用向下,就可以让节点最多的调整次数最少,也就是:多*少,少*多。
而向上调整,就是:多*多,少*少。第一层的节点少,不用调整,第二层两个节点,每个调整一次,后面节点多,每个节点调整次数也多。
第k-1层:2^(k-2)*1。
第k-2层:2^(k-3)*2。
……
第2层2^1*(k-2)。
第1层2^0*(k-1)。
总的:2^0*(k-1)+2^1*(k-2)+……+2^(k-2)*1=2^k+2*k-4。
O(N)=log N。
根据上面的结论,我们知道如果要建堆,那肯定是用向下调整更好。
🍩3.堆排序:
用向下排序拍好序以后,如果我们要排升序,我们就建大堆,如果我们要排降序,我们就排小队堆。
升序:大堆。
降序:小堆。
我们以升序为例:
当得到大堆的时候,根节点是最大的,然后我们把根节点和最后的节点换一下位置,这样最大的就到最后面去了,然后我们换完以后,又用向下调整使除最后一个节点以外为大堆,这样我们取根节点,我们就的得到了第二大的,我们就把第二大的和数组的倒数第2的位置换位置,然后再让根节点向下调整建立大堆……
这样我们就能让数组升序,代码实现:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void AdjustDown(int* a, int size, int parent)
{//假设法int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1]>a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//升序
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}相关文章:

【数据结构:排序算法】堆排序(图文详解)
🎁个人主页:我们的五年 🔍系列专栏:数据结构课程学习 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 🍩1.大堆和小堆 🍩2.向上调整算法建堆和向下调整算法建堆:…...

git 派生仓库怎么同步主仓库的新分支
一、git 派生仓库怎么同步主仓库的新分支 要使你的Git派生仓库同步主仓库的新分支,请遵循以下步骤: 1、添加上游仓库(如果尚未添加): 如之前所述,确保上游仓库已经被添加到你的本地仓库。如果没有,使用命…...

对比方案:5款知识中台工具的优缺点详解
知识中台工具为企业和组织高效地组织、存储和分享知识,还能提升团队协作的效率。在选择搭建知识中台的工具时,了解工具的优缺点,有助于企业做出最佳决策。本文LookLook同学将对五款搭建知识中台的工具进行优缺点的简单介绍,帮助企…...
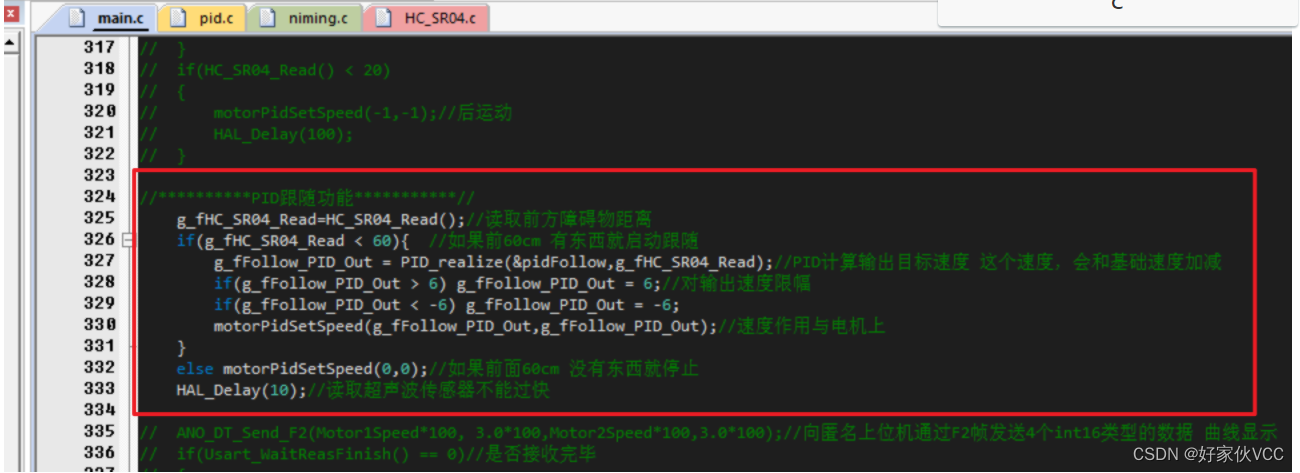
第16章-超声波跟随功能 基于STM32的三路超声波自动跟随小车 毕业设计 课程设计
第16章-超声波跟随功能 无PID跟随功能 //超声波跟随if(HC_SR04_Read() > 25){motorForward();//前进HAL_Delay(100);}if(HC_SR04_Read() < 20){motorBackward();//后退HAL_Delay(100);}PID跟随功能 在pid.c中定义一组PID参数 tPid pidFollow; //定距离跟随PIDpidFol…...

创新案例 | 持续增长,好孩子集团的全球化品牌矩阵战略与客户中心设计哲学
探索好孩子集团如何通过创新设计的全球化品牌矩阵和以客户为中心的产品策略,在竞争激烈的母婴市场中实现持续增长。深入了解其品牌价值观、市场定位策略以及如何满足新一代父母的需求。本文旨在为中高级职场人士、创业家及创新精英提供深度见解,帮助他们…...
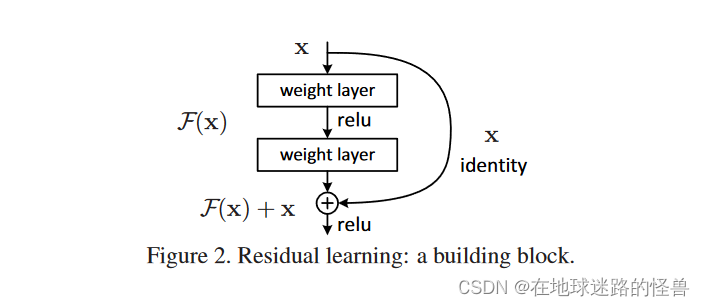
ResNet 原理剖析以及代码复现
原理 ResNet 解决了什么问题? 一言以蔽之:解决了深度的神经网络难以训练的问题。 具体的说,理论上神经网络的深度越深,其训练效果应该越好,但实际上并非如此,层数越深会导致越差的结果并且容易产生梯度爆炸…...
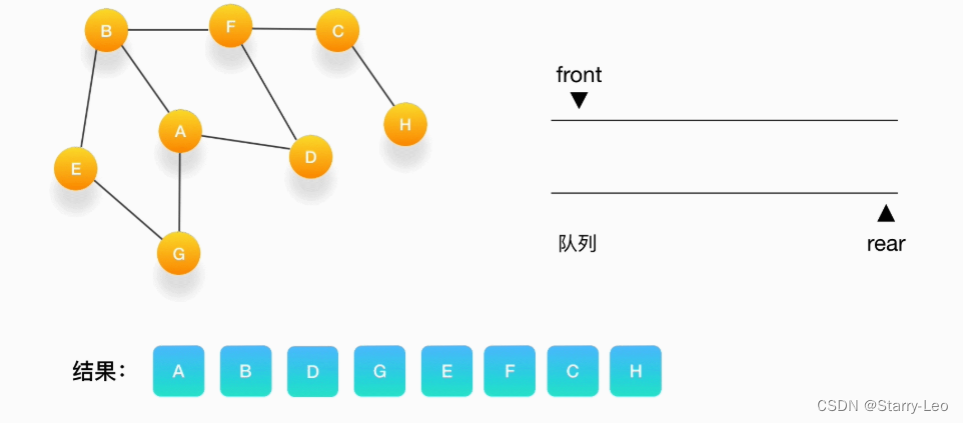
数据结构(十)图
文章目录 图的简介图的定义图的结构图的分类无向图有向图带权图(Wighted Graph) 图的存储邻接矩阵(Adjacency Matrix)邻接表代码实现 图的遍历深度优先搜索(DFS,Depth Fisrt Search)遍历抖索过程…...

四数之和-力扣
本题在三数之和的基础上,再增加一重循环进行解答 首先注意的点是,一级剪枝处理,target > 0 && nums[i] > target 此处只有整数才可剪枝处理,如果target为负数,nums[i] < target,也不能代…...
JS 中怎么删除数组元素?有哪几种方法?
正文开始之前推荐一位宝藏博主免费分享的学习教程,学起来! 编号学习链接1Cesium: 保姆级教程+源码示例2openlayers: 保姆级教程+源码示例3Leaflet: 保姆级教程+源码示例4MapboxGL: 保姆级教程+源码示例splice() JavaScript中的splice()方法是一个内置的数组对象函数, 用于…...

Git如何将pre-commit也提交到仓库
我一开始准备将pre-commit提交到仓库进行备份的,但是却发现提交不了,即使我使用强制提交都不行。 (main) $ git add ./.git/hooks/pre-commit(main) $ git status On branch main nothing to commit, working tree clean# 强制提交(main) $ git add -f .…...

vmware中Ubuntu虚拟机和本地电脑Win10互相ping通
初始状态 使用vmware17版本安装的Ubuntu的20版本,安装之后什么配置都要不懂,然后进行下述配置。 初始的时候是NAT,没动的. 设置 点击右键编辑“属性” 常规选择“启用”: 高级选择全部: 打开网络配置,右键属…...

比较含退格的字符串-力扣
做这道题时出现了许多问题 第一次做题思路是使用双指针去解决,快慢指针遇到字母则前进,遇到 # 则慢指针退1,最开始并未考虑到 slowindex < 0 ,从而导致越界。第二个问题在于,在最后判断两个字符串是否相同时,最初使…...

NSSCTF-Web题目4
[SWPUCTF 2021 新生赛]hardrce 1、题目 2、知识点 rce:远程代码执行、url取反编码 3、解题思路 打开题目 出现一段代码,审计源代码 题目需要我们通过get方式输入变量wllm的值 但是变量的值被过滤了,不能输入字母和\t、\n等值 所以我们需…...

7. CSS 网格布局
CSS3引入了强大的网格布局(Grid Layout),它提供了一种二维的布局方式,使得创建复杂的网页布局变得更加简单和直观。通过定义行和列,我们可以精确控制网页元素的排列和对齐。本章将详细介绍网格布局的基本概念和属性&am…...

如何配置才能连接远程服务器上的 redis server ?
文章目录 Intro修改点 Intro 以阿里云服为例。 首先,我在我买的阿里云服务器中以下载源码、手动编译的方式安装了 redis-server,操作流程见:Ubuntu redis 下载解压配置使用及密码管理 && 包管理工具联网安装。 接着,我…...
MindSpore实践图神经网络之环境篇
MindSpore在Windows11系统下的环境配置。 MindSpore环境配置大概分为三步:(1)安装Python环境,(2)安装MindSpore,(3)验证是否成功 如果是GPU环境还需安装CUDA等环境&…...

MVS net笔记和理解
文章目录 传统的方法有什么缺陷吗?MVSnet深度的预估 传统的方法有什么缺陷吗? 传统的mvs算法它对图像的光照要求相对较高,但是在实际中要保证照片的光照效果很好是很难的。所以传统算法对镜面反射,白墙这种的重建效果就比较差。 …...
)
Linux 编译屏障之 ACCESS_ONCE()
文章目录 1. 前言2. 背景3. 为什么要有 ACCESS_ONCE() ?4. ACCESS_ONCE() 代码实现5. ACCESS_ONCE() 实例分析6. ACCESS() 的演进7. 结语8. 参考资料 1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做…...

Discuz!X3.4论坛网站公安备案号怎样放到网站底部?
Discuz!网站的工信部备案号都知道在后台——全局——站点信息——网站备案信息代码填写,那公安备案号要添加在哪里呢?并没有看到公安备案号填写栏,今天驰网飞飞和你分享 1)工信部备案号和公安备案号统一填写到网站备案…...

LPDDR6带宽预计将翻倍增长:应对低功耗挑战与AI时代能源需求激增
在当前科技发展的背景下,低能耗问题成为了业界关注的焦点。国际能源署(IEA)近期报告显示,日常的数字活动对电力消耗产生显著影响——每次Google搜索平均消耗0.3瓦时(Wh),而向OpenAI的ChatGPT提出的每一次请求则消耗2.9…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
