ResNet 原理剖析以及代码复现
原理
ResNet 解决了什么问题?
一言以蔽之:解决了深度的神经网络难以训练的问题。
具体的说,理论上神经网络的深度越深,其训练效果应该越好,但实际上并非如此,层数越深会导致越差的结果并且容易产生梯度爆炸或梯度消失等问题。
ResNet 怎么解决的?
提出了一个残差学习网络的框架,该框架解决了上述问题。
残差网络的架构
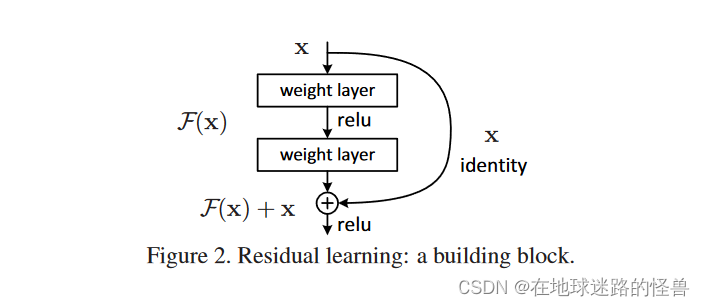
整个架构如上图所示。
首先我们要学习的东西是 H(x),假设现在已经有了一个浅的网络,然后我们要在上面新加一些层,让网络变得更深,如果按传统的做法那么新加的层就继续跟之前一样进行学习就行了。但是现在在新加的层中我们不直接去学 H(x),而是应该去学 H(x) - x。x 就是之前比较浅的网络已经学到的那个东西,也就是在新加的层中不去重新学个东西而只是学学到的东西和真实的东西二者之间的残差 H(x) - x,然后该层最后的输出结果 F(x) 再加上原始数据 x 就是最终结果也就是 F(x) + x ,此时优化的目标就不再是原始的 H(x),而是 H(x) - x 这个东西。
这就是 ResNet 的核心思想。
我感觉有一篇文章讲的很好,可以参考一下:ResNet网络详细讲解
下面是论文原文的描述:
在本文中,我们通过引入一个深度残差学习框架来解决退化问题。我们不希望每几个堆叠层直接拟合一个期望的底层映射,而是明确地让这些层拟合一个残差映射。在形式上,我们将期望的底层映射表示为H ( x ),并让堆叠的非线性层拟合F ( x )的另一个映射:= H ( x ) - x。原始映射被重铸成F ( x ) + x。我们假设优化残差映射比优化原始的、未引用的映射更容易。在极端情况下,如果一个恒等映射是最优的,那么将残差推到零比用一堆非线性层拟合一个恒等映射更容易。
F ( x ) + x的表达式可以通过具有"捷径连接"的前馈神经网络来实现(图2 )。快捷方式连接[ 2、33、48]是那些跳过一个或多个层的连接。在我们的例子中,快捷连接只是执行身份映射,它们的输出被添加到堆叠层的输出中(图2 )。身份捷径连接既不增加额外的参数,也不增加计算复杂度。整个网络仍然可以通过反向传播的SGD进行端到端的训练,并且可以很容易地使用公共库(例如, Caffe )实现,无需修改求解器。
我们在ImageNet [ 35 ]上进行了全面的实验来展示退化问题并评估我们的方法。研究表明:
1 )我们的深度残差网络易于优化,但对应的"普通"网络(简单地堆叠层)在深度增加时表现出更高的训练误差;
2 )我们的深度残差网络可以很容易地从大幅增加的深度中获得精度增益,产生的结果明显优于以前的网络。
在ImageNet分类数据集上[ 35 ],我们通过极深的残差网络获得了优异的结果。我们的152层残差网络是ImageNet上有史以来最深层的网络,但仍比VGG网络具有更低的复杂度[ 40 ]。我们的集成在ImageNet测试集上有3.57 %的top - 5误差,并在ILSVRC 2015分类竞赛中获得第一名。在其他识别任务上也具有出色的泛化性能,并引领我们在ILSVRC & COCO 2015竞赛中进一步获得第1名:ImageNet检测、ImageNet定位、COCO检测和COCO分割。这有力的证据表明,残差学习原理具有一般性,我们预期它在其他视觉和非视觉问题中也适用。
代码复现
这里给出我自己的模型代码:
import torch
from torch import nn# 基本残差块
class BasicBlock(nn.Module):expansion = 1"""参数解释:in_ch:输入通道数block_ch:输出通道数stride:步长,通过该参数我们就可以实现网络结构中特征图Size减半、通道数增加一倍的效果downSample:其本身也是一个网络,用来实现残差网络中的跳跃连接(也就是论文中虚线和实线)同时跳跃连接也是用来区别基本残差块和瓶颈残差块的,二者区别如下:基本残差块:输入输出通道数相同瓶颈残差块:输入输出通道数不同,需要进行升维操作才能对位相加另外二者的结构不同,可以通过论文看到"""def __init__(self, in_ch, block_ch, stride=1, downSample=None):super().__init__()self.downSample = downSample# 从网络结构图中可以看到,先进行第一层卷积self.conv1 = nn.Conv2d(in_ch, block_ch, kernel_size=3, stride=stride, padding=1, bias=False)# 在网络模型中添加一个二维批归一化(Batch Normalization)层。# 批归一化是一种用于加速神经网络训练并提高其性能的技术,类似于将上面所输出的数据进行了统一整理self.bn1 = nn.BatchNorm2d(block_ch)# 激活函数self.relu1 = nn.ReLU()# 第二层卷积self.conv2 = nn.Conv2d(block_ch, block_ch * self.expansion, kernel_size=3, stride=1, padding=1, bias=False)self.bn2 = nn.BatchNorm2d(block_ch * self.expansion)self.relu2 = nn.ReLU()def forward(self, x):identity = x# 如果downSample参数不为空,说明其需要升维(也就是论文中虚线的样子)if self.downSample is not None:# 升维,让输入输出的通道数对齐identity = self.downSample(x)out = self.relu1(self.bn1(self.conv1(x)))out = self.bn2(self.conv2(out))# 这里就是论文中的输出与原始输入进对位相加的步骤out += identity# 对位相加结束后再进行 relu 函数的激活,然后输出结果return self.relu2(out)# 瓶颈残差块
class Bottleneck(nn.Module):# 从论文的网络结构图中不难发现,瓶颈残差块在第三层卷积时通道数会放大四倍# 因此定义一个 expansion 变量expansion = 4"""参数解释:in_ch:输入通道数block_ch:输出通道数stride:步长,通过该参数我们就可以实现网络结构中特征图Size减半、通道数增加一倍的效果downSample:其本身也是一个网络,用来实现残差网络中的跳跃连接(也就是论文中虚线和实线)同时跳跃连接也是用来区别基本残差块和瓶颈残差块的,二者区别如下:基本残差块:输入输出通道数相同瓶颈残差块:输入输出通道数不同,需要进行升维操作才能对位相加另外二者的结构不同,可以通过论文看到"""def __init__(self, in_ch, block_ch, stride=1, downSample=None):super().__init__()self.downSample = downSample# 从网络结构图中可以看到,先进行第一层卷积self.conv1 = nn.Conv2d(in_ch, block_ch, kernel_size=1, stride=stride, bias=False)# 在网络模型中添加一个二维批归一化(Batch Normalization)层。# 批归一化是一种用于加速神经网络训练并提高其性能的技术,类似于将上面所输出的数据进行了统一整理self.bn1 = nn.BatchNorm2d(block_ch)# 激活函数self.relu1 = nn.ReLU()# 第二层卷积self.conv2 = nn.Conv2d(block_ch, block_ch, kernel_size=3, stride=1, padding=1, bias=False)self.bn2 = nn.BatchNorm2d(block_ch)self.relu2 = nn.ReLU()# 第三层卷积self.conv3 = nn.Conv2d(block_ch, block_ch * self.expansion, kernel_size=1, stride=1, bias=False)self.bn3 = nn.BatchNorm2d(block_ch * self.expansion)self.relu3 = nn.ReLU()def forward(self, x):identity = x# 如果downSample参数不为空,说明其需要升维(也就是论文中虚线的样子)if self.downSample is not None:# 升维,让输入输出的通道数对齐identity = self.downSample(x)out = self.relu1(self.bn1(self.conv1(x)))out = self.relu2(self.bn2(self.conv2(out)))out = self.bn3(self.conv3(out))# 这里就是论文中的输出与原始输入进对位相加的步骤out += identity# 对位相加结束后再进行 relu 函数的激活,然后输出结果return self.relu3(out)# 残差网络
class ResNet(nn.Module):"""in_ch: 默认为3,因为残差网络就是用来图片分类的,所以输入通道数默认为 3num_classes:分类的数量,默认设置为100,即 100 种分类block:用来区别是 基本残差块 还是 瓶颈残差块block_num:每个残差块所需要堆叠的次数(也是论文中提供的有)"""def __init__(self, in_ch=3, num_classes=100, block=Bottleneck, block_num=[3, 4, 6, 3]):super().__init__()# 因为在各层之间通道数会发生变化,因此要进行跟踪self.in_ch = in_ch# 对于残差网络来说,不管是什么类型其一开始都要进行 7x7 的卷积和 3x3 的池化# 因此我们直接照搬即可(论文中已经有了)self.conv1 = nn.Conv2d(in_ch, 64, kernel_size=7, stride=2, padding=3, bias=False)self.bn1 = nn.BatchNorm2d(64)self.maxpool1 = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)self.in_ch = 64# 将残差块堆叠起来,形成一个一个的残差层,进而构建成ResNetself.layer1 = self._make_layer(block, 64, block_num[0], stride=1)self.layer2 = self._make_layer(block, 128, block_num[1], stride=2)self.layer3 = self._make_layer(block, 256, block_num[2], stride=2)self.layer4 = self._make_layer(block, 512, block_num[3], stride=2)# 最后是全连接层,做预测的self.fc_layer = nn.Sequential(nn.Linear(512*block.expansion*7*7, num_classes),nn.Softmax(dim=-1))def _make_layer(self, block, block_ch, block_num, stride=2):layers = []downSample = nn.Conv2d(self.in_ch, block_ch * block.expansion, kernel_size=1, stride=stride)layers += [block(self.in_ch, block_ch, stride=stride, downSample=downSample)]self.in_ch = block_ch * block.expansionfor _ in range(1, block_num):layers += [block(self.in_ch, block_ch)]return nn.Sequential(*layers)def forward(self, x):out = self.maxpool1(self.bn1(self.conv1(x))) #(1, 3, 224, 224) -> (1, 64, 56, 56)out = self.layer1(out)out = self.layer2(out)out = self.layer3(out)out = self.layer4(out)out = out.reshape(out.shape[0], -1)out = self.fc_layer(out)return outif __name__ == '__main__':# 接下来进行测试# 这行代码创建了一个形状为 (1, 3, 224, 224) 的四维张量 x,# 其中包含了一个大小为 1 的批次中的一个 224x224 像素的 RGB 图像。x = torch.randn(1, 3, 224, 224)resnet = ResNet(in_ch=3, num_classes=100, block=Bottleneck, block_num=[2, 2, 2, 2])y = resnet(x)print(y.shape)相关文章:

ResNet 原理剖析以及代码复现
原理 ResNet 解决了什么问题? 一言以蔽之:解决了深度的神经网络难以训练的问题。 具体的说,理论上神经网络的深度越深,其训练效果应该越好,但实际上并非如此,层数越深会导致越差的结果并且容易产生梯度爆炸…...
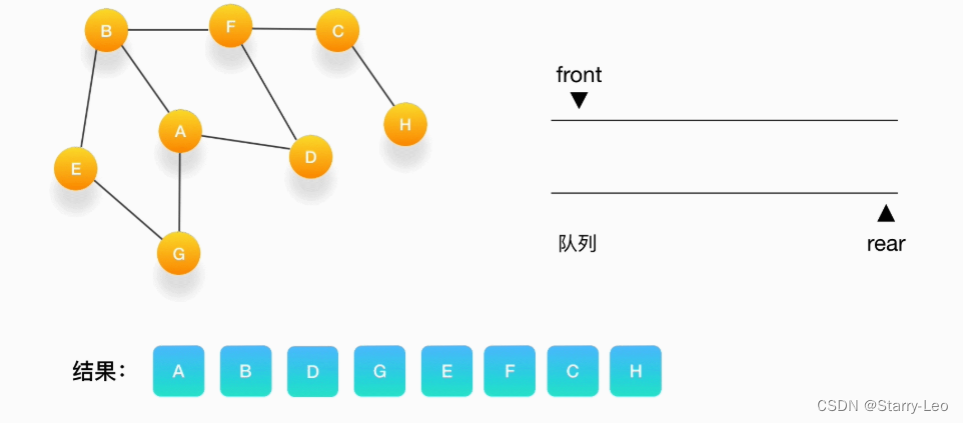
数据结构(十)图
文章目录 图的简介图的定义图的结构图的分类无向图有向图带权图(Wighted Graph) 图的存储邻接矩阵(Adjacency Matrix)邻接表代码实现 图的遍历深度优先搜索(DFS,Depth Fisrt Search)遍历抖索过程…...

四数之和-力扣
本题在三数之和的基础上,再增加一重循环进行解答 首先注意的点是,一级剪枝处理,target > 0 && nums[i] > target 此处只有整数才可剪枝处理,如果target为负数,nums[i] < target,也不能代…...
JS 中怎么删除数组元素?有哪几种方法?
正文开始之前推荐一位宝藏博主免费分享的学习教程,学起来! 编号学习链接1Cesium: 保姆级教程+源码示例2openlayers: 保姆级教程+源码示例3Leaflet: 保姆级教程+源码示例4MapboxGL: 保姆级教程+源码示例splice() JavaScript中的splice()方法是一个内置的数组对象函数, 用于…...

Git如何将pre-commit也提交到仓库
我一开始准备将pre-commit提交到仓库进行备份的,但是却发现提交不了,即使我使用强制提交都不行。 (main) $ git add ./.git/hooks/pre-commit(main) $ git status On branch main nothing to commit, working tree clean# 强制提交(main) $ git add -f .…...

vmware中Ubuntu虚拟机和本地电脑Win10互相ping通
初始状态 使用vmware17版本安装的Ubuntu的20版本,安装之后什么配置都要不懂,然后进行下述配置。 初始的时候是NAT,没动的. 设置 点击右键编辑“属性” 常规选择“启用”: 高级选择全部: 打开网络配置,右键属…...

比较含退格的字符串-力扣
做这道题时出现了许多问题 第一次做题思路是使用双指针去解决,快慢指针遇到字母则前进,遇到 # 则慢指针退1,最开始并未考虑到 slowindex < 0 ,从而导致越界。第二个问题在于,在最后判断两个字符串是否相同时,最初使…...

NSSCTF-Web题目4
[SWPUCTF 2021 新生赛]hardrce 1、题目 2、知识点 rce:远程代码执行、url取反编码 3、解题思路 打开题目 出现一段代码,审计源代码 题目需要我们通过get方式输入变量wllm的值 但是变量的值被过滤了,不能输入字母和\t、\n等值 所以我们需…...

7. CSS 网格布局
CSS3引入了强大的网格布局(Grid Layout),它提供了一种二维的布局方式,使得创建复杂的网页布局变得更加简单和直观。通过定义行和列,我们可以精确控制网页元素的排列和对齐。本章将详细介绍网格布局的基本概念和属性&am…...

如何配置才能连接远程服务器上的 redis server ?
文章目录 Intro修改点 Intro 以阿里云服为例。 首先,我在我买的阿里云服务器中以下载源码、手动编译的方式安装了 redis-server,操作流程见:Ubuntu redis 下载解压配置使用及密码管理 && 包管理工具联网安装。 接着,我…...
MindSpore实践图神经网络之环境篇
MindSpore在Windows11系统下的环境配置。 MindSpore环境配置大概分为三步:(1)安装Python环境,(2)安装MindSpore,(3)验证是否成功 如果是GPU环境还需安装CUDA等环境&…...

MVS net笔记和理解
文章目录 传统的方法有什么缺陷吗?MVSnet深度的预估 传统的方法有什么缺陷吗? 传统的mvs算法它对图像的光照要求相对较高,但是在实际中要保证照片的光照效果很好是很难的。所以传统算法对镜面反射,白墙这种的重建效果就比较差。 …...
)
Linux 编译屏障之 ACCESS_ONCE()
文章目录 1. 前言2. 背景3. 为什么要有 ACCESS_ONCE() ?4. ACCESS_ONCE() 代码实现5. ACCESS_ONCE() 实例分析6. ACCESS() 的演进7. 结语8. 参考资料 1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做…...

Discuz!X3.4论坛网站公安备案号怎样放到网站底部?
Discuz!网站的工信部备案号都知道在后台——全局——站点信息——网站备案信息代码填写,那公安备案号要添加在哪里呢?并没有看到公安备案号填写栏,今天驰网飞飞和你分享 1)工信部备案号和公安备案号统一填写到网站备案…...

LPDDR6带宽预计将翻倍增长:应对低功耗挑战与AI时代能源需求激增
在当前科技发展的背景下,低能耗问题成为了业界关注的焦点。国际能源署(IEA)近期报告显示,日常的数字活动对电力消耗产生显著影响——每次Google搜索平均消耗0.3瓦时(Wh),而向OpenAI的ChatGPT提出的每一次请求则消耗2.9…...

云原生架构内涵_3.主要架构模式
云原生架构有非常多的架构模式,这里列举一些对应用收益更大的主要架构模式,如服务化架构模式、Mesh化架构模式、Serverless模式、存储计算分离模式、分布式事务模式、可观测架构、事件驱动架构等。 1.服务化架构模式 服务化架构是云时代构建云原生应用的…...

宏基因组分析流程(Metagenomic workflow)202405|持续更新
Logs 增加R包pctax内的一些帮助上游分析的小脚本(2024.03.03)增加Mmseqs2用于去冗余,基因聚类的速度非常快,且随序列量线性增长(2024.03.12)更新全文细节(2024.05.29) 注意&#x…...
)
一千题,No.0037(组个最小数)
给定数字 0-9 各若干个。你可以以任意顺序排列这些数字,但必须全部使用。目标是使得最后得到的数尽可能小(注意 0 不能做首位)。例如:给定两个 0,两个 1,三个 5,一个 8,我们得到的最…...

PV PVC
默写 1 如何将pod创建在指定的Node节点上 node亲和、pod亲和、pod反亲和: 调度策略 匹配标签 操作符 nodeAffinity 主机 In,NotIn,Exists,DoesNotExist,Gt,Lt podAffinity …...

深入理解Nginx配置文件:全面指南
Nginx 是一个高性能的 HTTP 服务器和反向代理服务器,也是一个电子邮件(IMAP/POP3)代理服务器。由于其高效性和灵活性,Nginx 被广泛应用于各种 web 服务中。本文将详细介绍 Nginx 配置文件的结构和主要配置项,帮助你深入…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
