Codeforces Round 895 (Div. 3)(A,B,C)题解(自己VP的,没有参加这场比赛)
A. Two Vessels

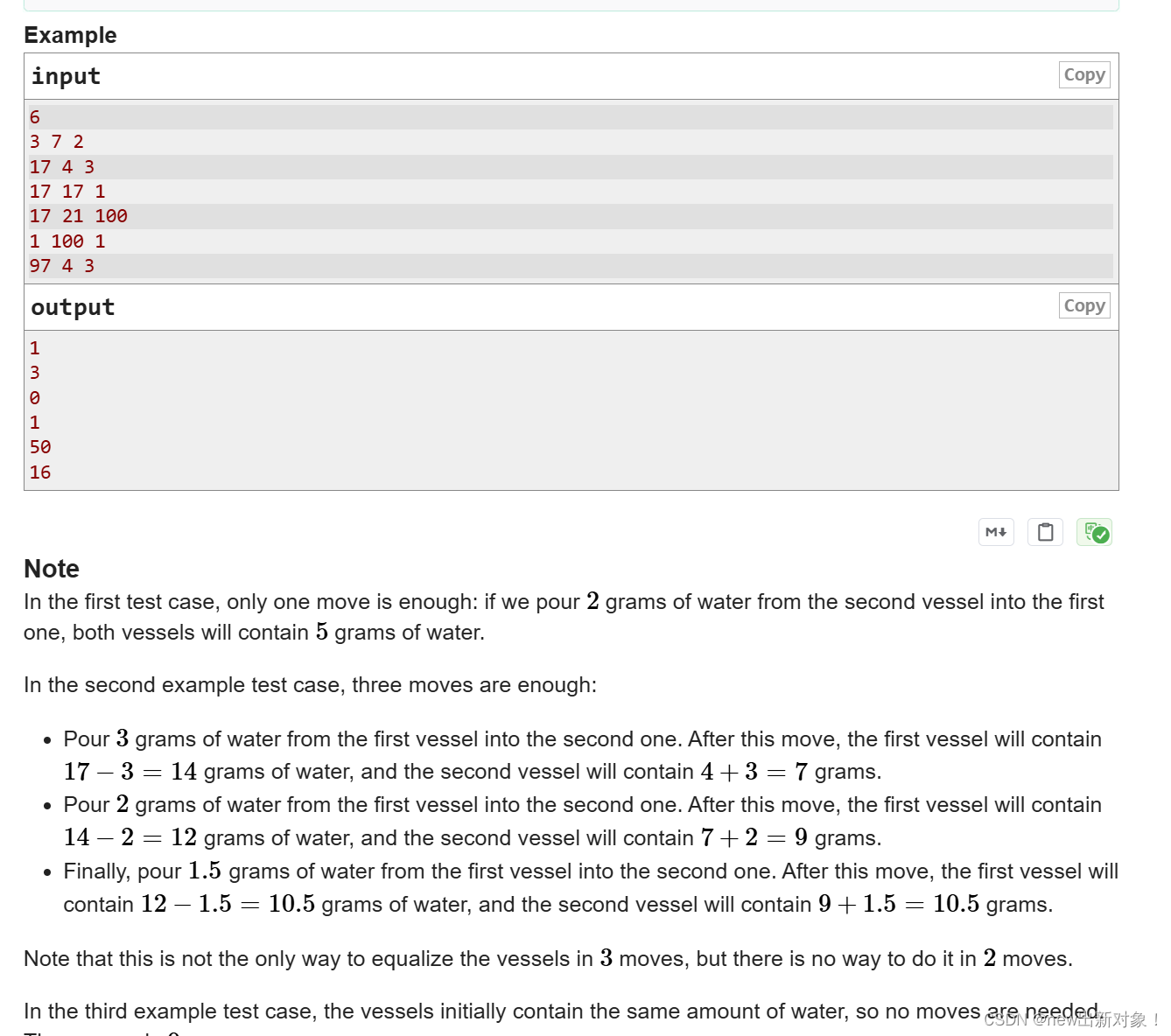
题解: 这题直接计算两个杯子之间的差值,然后直接除以2倍杯子的容量直接过,没有任何难度
#include<bits/stdc++.h>
using namespace std;int t;
int a,b,c;int main()
{cin>>t;while(t--){cin>>a>>b>>c;int flag=abs(a-b);//计算差值int num=flag/(2*c);//计算次数if(flag%(2*c)!=0)num++;cout<<num<<"\n"; }return 0;
}B. The Corridor or There and Back Again

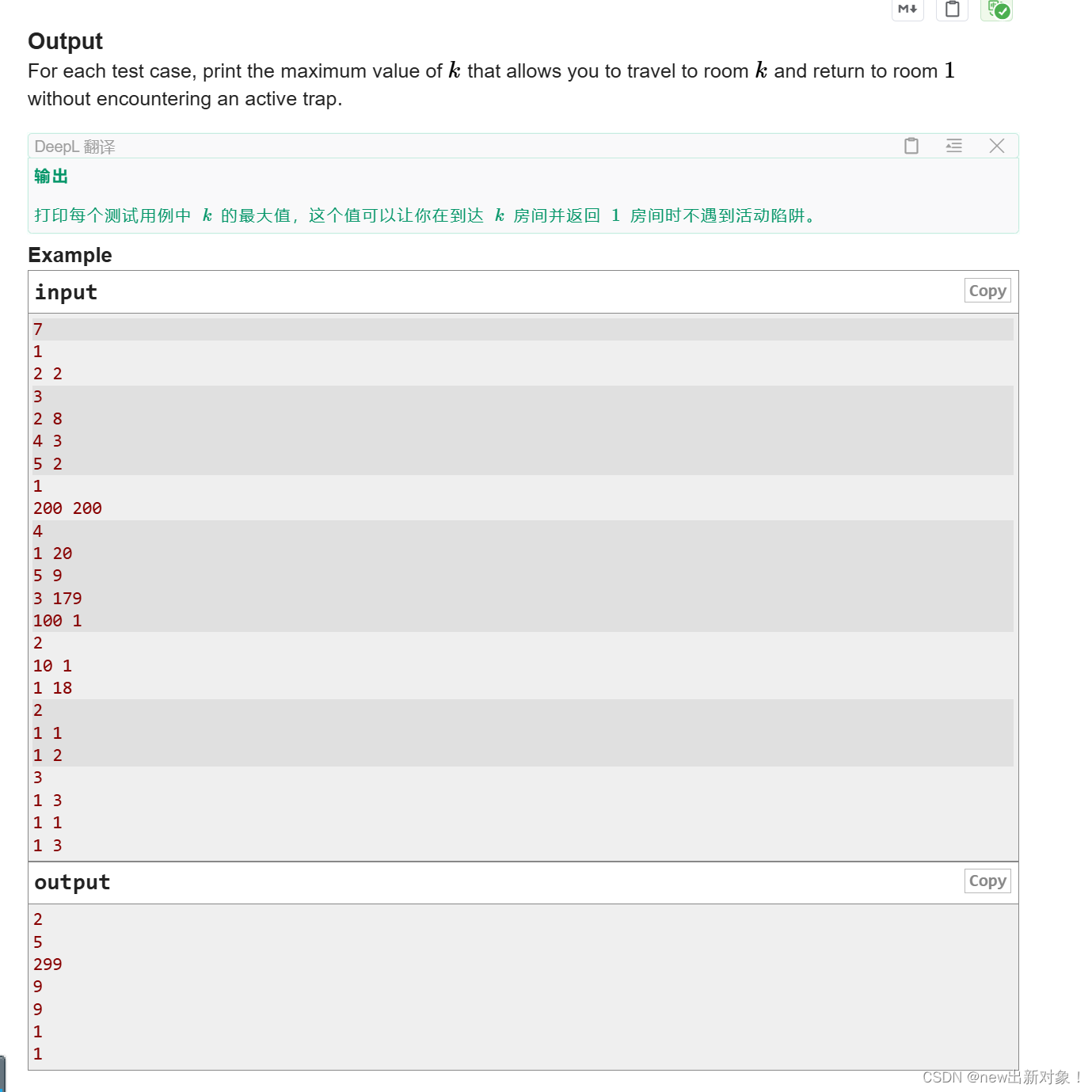
题解:这题咋说嘞,用一个数,去统计每个有陷阱的房间最多允许我去的最右边的房间是多少,然后取其中最小的一个就是我们要求的结果,也是没啥难度
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
int d;
int s;
int minn=0x3f3f3f3f;
int main()
{cin>>t;while(t--){minn=0x3f3f3f3f;cin>>n;for(int i=1;i<=n;i++){cin>>d>>s;if(s%2==0)minn=min(minn,s/2-1+d);else{minn=min(minn,s/2+d);}}cout<<minn<<"\n";}return 0;
}C. Non-coprime Split


题解:这题要想做出来,需要知道一个知识点,求最大公约数除了欧几里得法(辗转相除法)还有一个就是更相减损术,gcd(a,b)=gcd(a-b,b)(前提是a>b)然后对于第二个公式来讲,那么就是a+b=第一个公式的a,然后就有做这题的眉目了,我们可以将要从左区间开找,找到一个因子即可返回i-因子和因子的值
#include<bits/stdc++.h>
using namespace std;
int t;
int l,r;
int main()
{cin>>t;while(t--){cin>>l>>r;int flag=0;for(int i=max(l,4);i<=r;i++){for(int j=2;j<=i/j;j++){if(i%j==0){flag=1;printf("%d %d\n",i-j,j);break;}}if(flag==1){break;}} if(flag==0)printf("-1\n");}return 0;
}
相关文章:

Codeforces Round 895 (Div. 3)(A,B,C)题解(自己VP的,没有参加这场比赛)
A. Two Vessels 题解: 这题直接计算两个杯子之间的差值,然后直接除以2倍杯子的容量直接过,没有任何难度 #include<bits/stdc.h> using namespace std;int t; int a,b,c;int main() {cin>>t;while(t--){cin>>a>>b>…...

9秒爬取庆余年2分集剧情
版本一: 要创建一个Python爬虫程序来爬取指定网站的分集剧情,我们需要使用requests库来发送HTTP请求,以及BeautifulSoup库来解析HTML内容。以下是一个简单的示例,展示了如何爬取你提供的网站的分集剧情,并将每集剧情保存到本地的.txt文件中。 首先,确保你已经安装了req…...

阿里云布置net core 项目
一、 创建镜像 给镜像添加触发器,编译的时候会触发k8s集群里的taget链接,从而更新项目 二,创建k8s集群 使用镜像创建 添加基本信息 镜像名称:镜像仓库》基本信息公网地址镜像Tag:创建镜像时的镜像版本镜像配置为:总…...

两整数之和 ---- 位运算
题目链接 题目: 分析: 题目中要求不能使用-, 考虑到我们的位运算异或^, 是无进位加法, 可以使用如果是无进位加法, 那么我们就要找到进位, 并进行计算, 进位只有1和1相加时才会产生进位1, 而0和1相加无进位, 进位为0, 那么我们就想到了&运算, 1&1 1, 0&1 0, 所…...

长城电脑压缩文件丢失了怎么办?怎么解决
在数字化时代,电脑已成为我们日常生活和工作中不可或缺的设备。长城电脑作为国内知名品牌,以其稳定可靠的性能赢得了广大用户的信赖。然而,即便是可靠的电脑,也难免会遇到一些问题。其中,压缩文件丢失无疑是一个令人头…...

论文笔记《基于深度学习模型的药物-靶标结合亲和力预测》
基于深度学习模型的药物-靶标结合亲和力预测 这是一篇二区的文章,算是一个综述,记录一下在阅读过程中遇到的问题。 文章目录 基于深度学习模型的药物-靶标结合亲和力预测前言一、蛋白质接触图谱二、为什么蛋白质图谱的准确性对DTA模型预测结果没有影响1…...

ArrayList和LinkedList对比,ArrayList使用注意事项
ArrayList和LinkedList对比,ArrayList使用注意事项 ArrayList 和 LinkedList 是 Java 中常用的两种集合类,它们在内部实现和性能上有一些重要的区别。 ArrayList: ArrayList 是基于动态数组实现的。它内部使用一个数组来存储元素,当数组空间…...
小熊家务帮day5-day7 客户管理模块1 (小程序认证,手机验证码认证,账号密码认证,修改密码,找回密码等)
客户管理模块 1.认证模块1.1 认证方式介绍1.1.1 小程序认证1.1.2 手机验证码登录1.1.3 账号密码认证 1.2 小程序认证1.2.1 小程序申请1.2.2 创建客户后端工程jzo2o-customer1.2.3 开发部署前端1.2.4 小程序认证流程1.2.4.1 customer小程序认证接口设计Controller层Service层调用…...

计算机图形学入门02:线性代数基础
1.向量(Vetors) 向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。 向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。 1.1向量点乘(…...
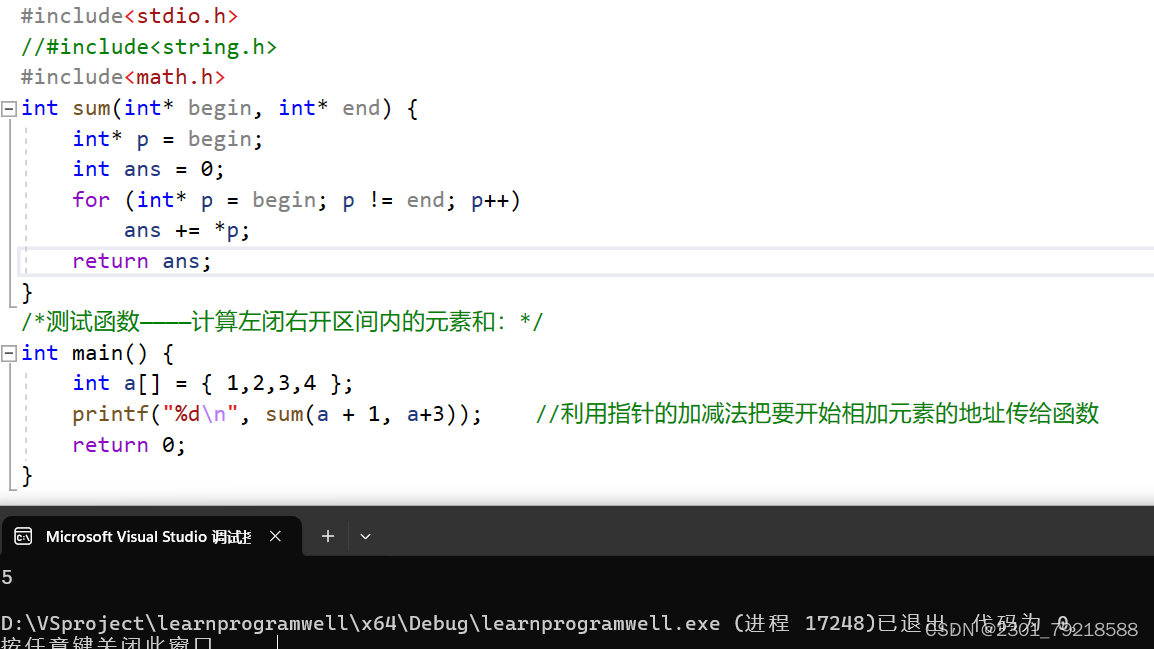
函数:计算数组的元素和
一、计算数组的元素和 参数传递给函数时,实际上只有数组的首地址作为指针传递给了函数。 在函数定义中的int a[ ]等价于int *a。在只有地址信息的情况下,是无法知道数组里有多少个元素的,因此在计算数组中的元素和时,要加一个参…...

如何进行数据库分库分表
当数据库的数据量增长到一定程度,单一数据库或表可能会遇到性能瓶颈,此时分库分表是一种常见的解决方案。以下是如何进行数据库分库分表的详细步骤和考虑因素,结合了参考文章中的相关信息: 一、分库分表概述 分库分表是为了解决…...
Spring-Cloud-CircuitBreaker-Resilience4j (3.1.1)
介绍 Resilience4j 是一个专为函数式编程而设计的轻量级容错库。Resilience4j 提供高阶函数(装饰器),以增强任何功能接口、lambda 表达式或方法引用,包括断路器、速率限制器、重试或隔板。您可以在任何函数接口、lambda 表达式或…...
)
重构与优化-组织数据(3)
重构组织数据是一个系统性的工程,旨在改进数据的存储方式、访问效率、质量和可用性,以更好地支持业务运营、分析决策和未来发展。以下是重构组织数据的一些关键说明点: 目的与动机 提升效率:通过优化数据结构、减少冗余数据和改善索引策略,加快数据查询和处理速度。 增强…...
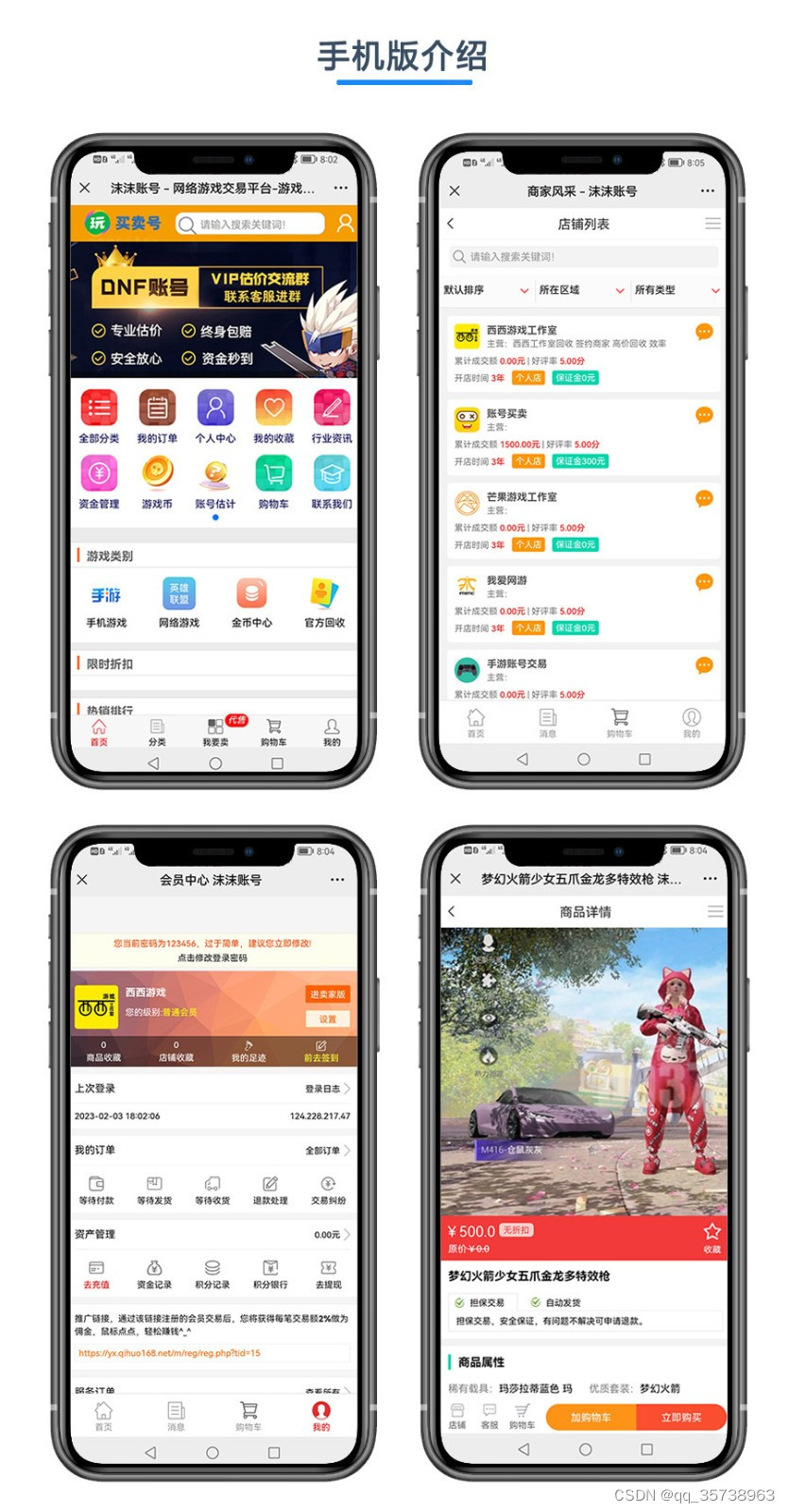
游戏交易平台源码游戏帐号交易平台系统源码
功能介绍 1:后台可以添加删除游戏分类 2:会员中心可以出售游戏币,账号,装备 3:后台可以对会员和商品进行管理 4:多商家入驻,商家发布信息 5:手机版功能可以生成APP 6:在线支付可支持微信和支…...

Matlab里面的浮点数与FPGA定点数的相互转化应用(含Matlab代码,封装成函数可直接调用)
微信公众号获取更多FPGA相关源码: 1.前言 Matlab里面计算通常用的是浮点数,而FPGA在做数字信号处理时,为了节约资源,常常使用的是定点数。在实践中,我们经常需要将Matlab实现中的算法,用FPGA进行实现。 …...

机器学习笔记——欠拟合、过拟合
欠拟合 将训练损失和测试损失都比较大的拟合叫欠拟合,那么他的预测精度很低 1.一般出现在模型的复杂度小于数据本身的复杂度导致的,这个可能就是模型对数据的分布和实际数据分布之间的差异,这个就可能需要更换模型 2.还可能出现在梯度下降算…...

【二进制部署k8s-1.29.4】七、验证master的安装
文章目录 简介 一.确认kubectl命令是否正常运行二.确认etcd安装是否正常运行三.确认kube-apiserver,kube-controller-manager,kube-scheduler安装是否正常四.配置apiserver和kubelet的访问授权五.master端安装脚本4.1.安装master端所需文件4.2.master快捷安装脚本 简介 本章节主…...

springboot获取当前数据库连接
要获取当前 Spring DataSource 的 URL,可以通过以下几种方法: 方法一:使用 JdbcTemplate 如果你使用的是 Spring 的 JdbcTemplate,可以通过 javax.sql.DataSource 获取连接,再获取它的 URL。 示例代码: …...
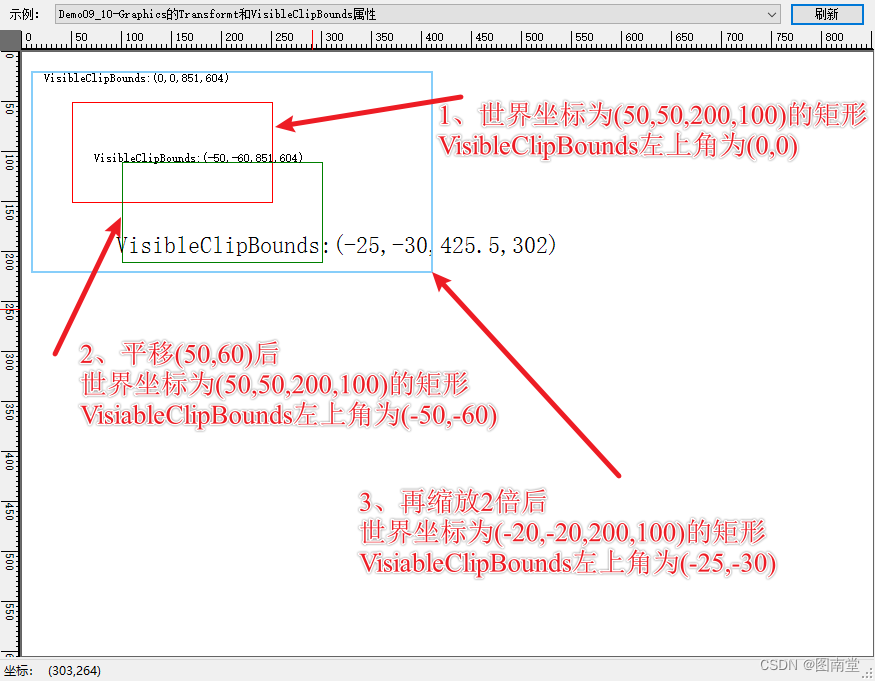
【学习笔记】Windows GDI绘图(九)Graphics详解(上)
文章目录 Graphics 定义创建Graphics对象的方法通过Graphics绘制不同的形状、线条、图像和文字等通过Graphics操作对象坐标 Graphics属性Clip(裁切/绘制区域)ClipBounds获取裁切区域矩形范围CompositiongMode合成方式CompositingQuality渲染质量DpiX和DpiY 水平、垂直分辨率Int…...

公告:公众号铁粉粉丝介绍以及说明
大家好,我是公众号博主--夏目 机械电气电机杂谈是我个人建立,为分享机械,电气,电机知识为主,闲谈杂聊社会时事,职场见闻,生活琐事,成长趣事,学习心得,读书观影…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
