【数据结构与算法 | 二叉树篇】二叉树的前中后序遍历(递归版本)
1. 二叉树的概念
(1). 二叉树的结构
借用了一下力扣的模板
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}(2). 完全二叉树与满二叉树
概念这玩意还是几个月前看王卓老师的视频里学的,现在看的认识,但描述起来有点便秘啊有木有. 还可能讲错了.
(1). 满二叉树就是最后一层只有叶子节点,除最后一层以外全是度为2的节点.
(2). 完全二叉树就是只有度为2与度为0的节点.只有最后一层会出现叶子节点.
2. 力扣144 : 二叉树的前序遍历
(1). 题
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
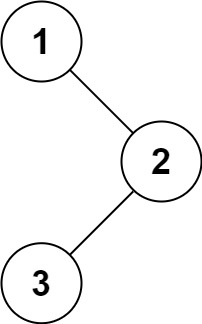
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:
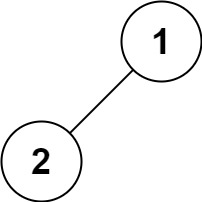
输入:root = [1,2] 输出:[1,2]
示例 5:
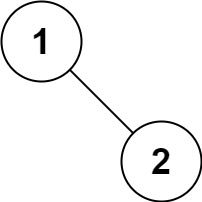
输入:root = [1,null,2] 输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
(2). 思路
口诀怼他个,前序遍历根左右.
(3). 解
class Solution {List<Integer> al = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {reverse(root);return al;}public void reverse(TreeNode root) {if (root == null) {return;}al.add(root.val);reverse(root.left);reverse(root.right);}
}3. 力扣94 : 二叉树的中序遍历
(1). 题
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
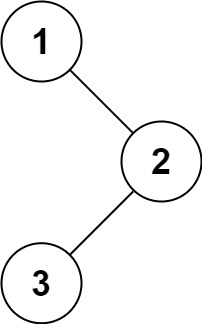
输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
(2). 思路
口诀,左根右.
(3). 解
class Solution {List<Integer> al = new ArrayList<>();public List<Integer> inorderTraversal(TreeNode root) {reverse(root);return al;}public void reverse(TreeNode root) {if (root == null) {return;}reverse(root.left);al.add(root.val);reverse(root.right);}
}4. 力扣145 : 二叉树的后序遍历
(1). 题
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
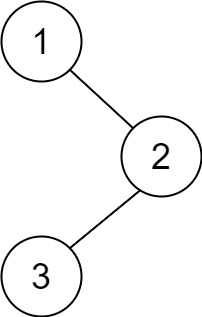
输入:root = [1,null,2,3] 输出:[3,2,1]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
(2). 思路
口诀,左右根搞定.
(3). 解
class Solution {List<Integer> al = new ArrayList<>();public List<Integer> postorderTraversal(TreeNode root) {reverse(root);return al;}public void reverse(TreeNode root) {if (root == null) {return;}reverse(root.left);reverse(root.right);al.add(root.val);}
}相关文章:

【数据结构与算法 | 二叉树篇】二叉树的前中后序遍历(递归版本)
1. 二叉树的概念 (1). 二叉树的结构 借用了一下力扣的模板 public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val val;this.left left;this.righ…...

Python exp用法:深入探索指数函数的奥秘
Python exp用法:深入探索指数函数的奥秘 在Python中,exp是一个非常重要的数学函数,它属于math模块的一部分,用于计算自然数e的指数。自然数e是一个无理数,约等于2.71828,它在数学、物理和工程等领域有着广…...
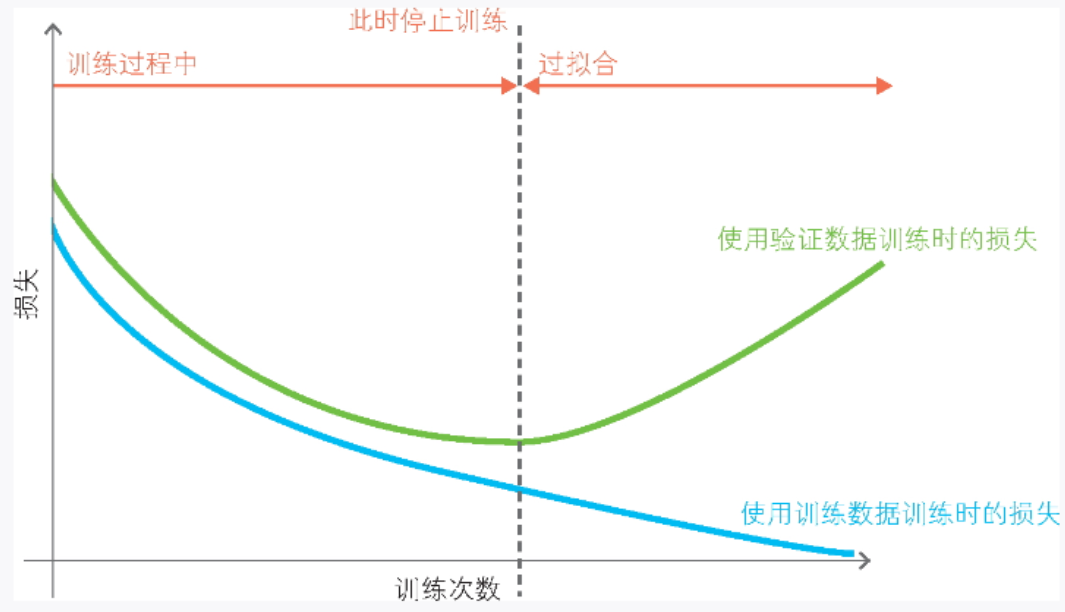
[有监督学习] 8.详细图解神经网络
神经网络 一直以来,人们都认为神经网络(Neural Network,NN)是模仿生物体的神经网络设计而成的。神经网络既可以用于回归,也可以用于分类,但在实际应用中常用于分类。基于神经网络的深 度学习因在图像识别和…...
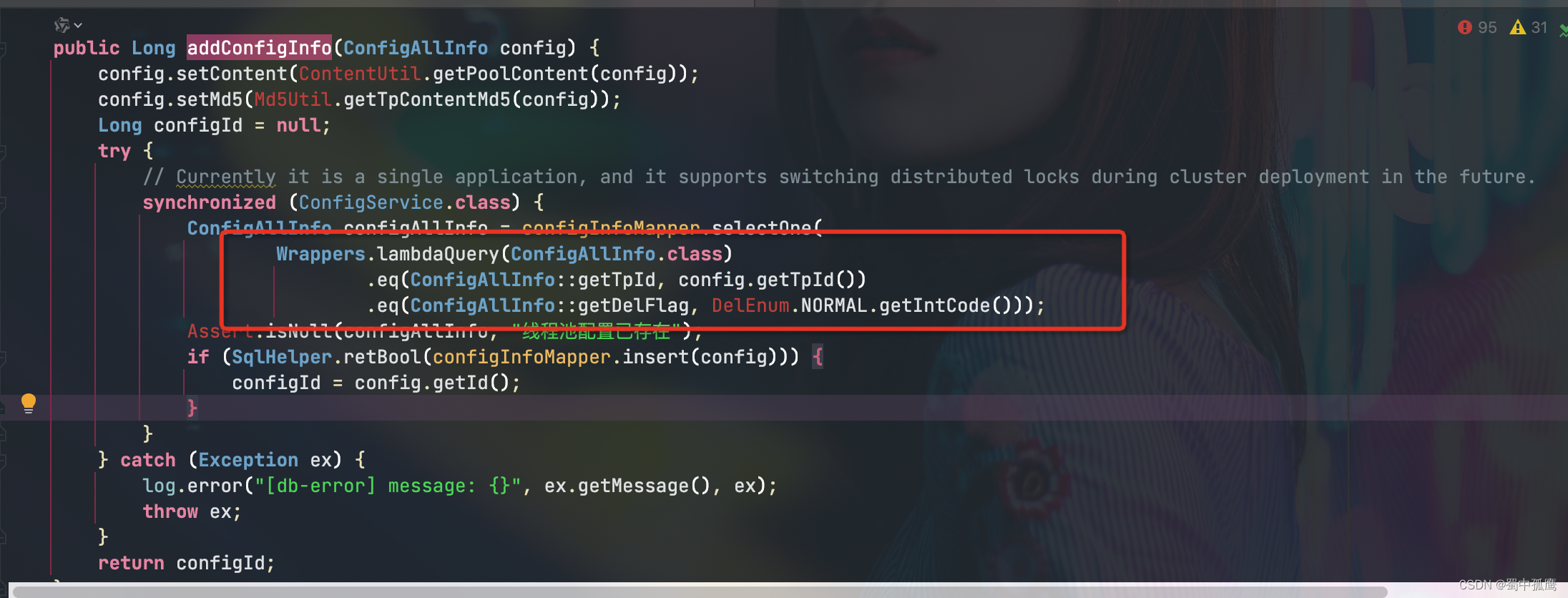
我给线程池管理框架hippo4j找bug
1 虚拟机参数不生效 hippo4j的docker启动脚本位于 docker/docker-startup.sh 。从下图可以看到 JAVA_OPT放在了jar包名 hippo4j-server.jar之后,而只有项目参数才放在jar包名之后。 实际上这里JAVA_OPT中包含虚拟机参数,而虚拟机参数要放在jar包名之前…...

win10键盘按乱了,如何恢复?
今天键盘被宝宝给按乱了,好不容易给重新调整回来,记录备忘: 1、win10的asdw和方向键互换了: 使用Fnw键来回切换,OK! 2、键盘的win键失效,例如:按winD无法显示桌面。此时…...

5.29工效学-人因工程人机交互
对于工效学这门课,一直都感觉很有意思,是一个值得再认真一点的课。可惜上课的时候效率不高,有感兴趣的东西课后也没有自行去拓展开来,前面的课我感觉还讲了比较重要的东西,但是,全忘了呢(真的对…...

头歌数据结构与算法课程设计中-硬币找零
给定n种不同面值的硬币k_i和每种硬币的数量x_i以及一个总金额k,请编写一个程序计算最少需要几枚硬币凑出这个金额k,凑出的方案是什么? 如果凑不出则输出“凑不出” 输入描述: 第一行两个正整数,n和k 然后n行每行两个数k_i和x_i 表示k_i面值的硬币有x_i个,中间以空格分隔 输…...
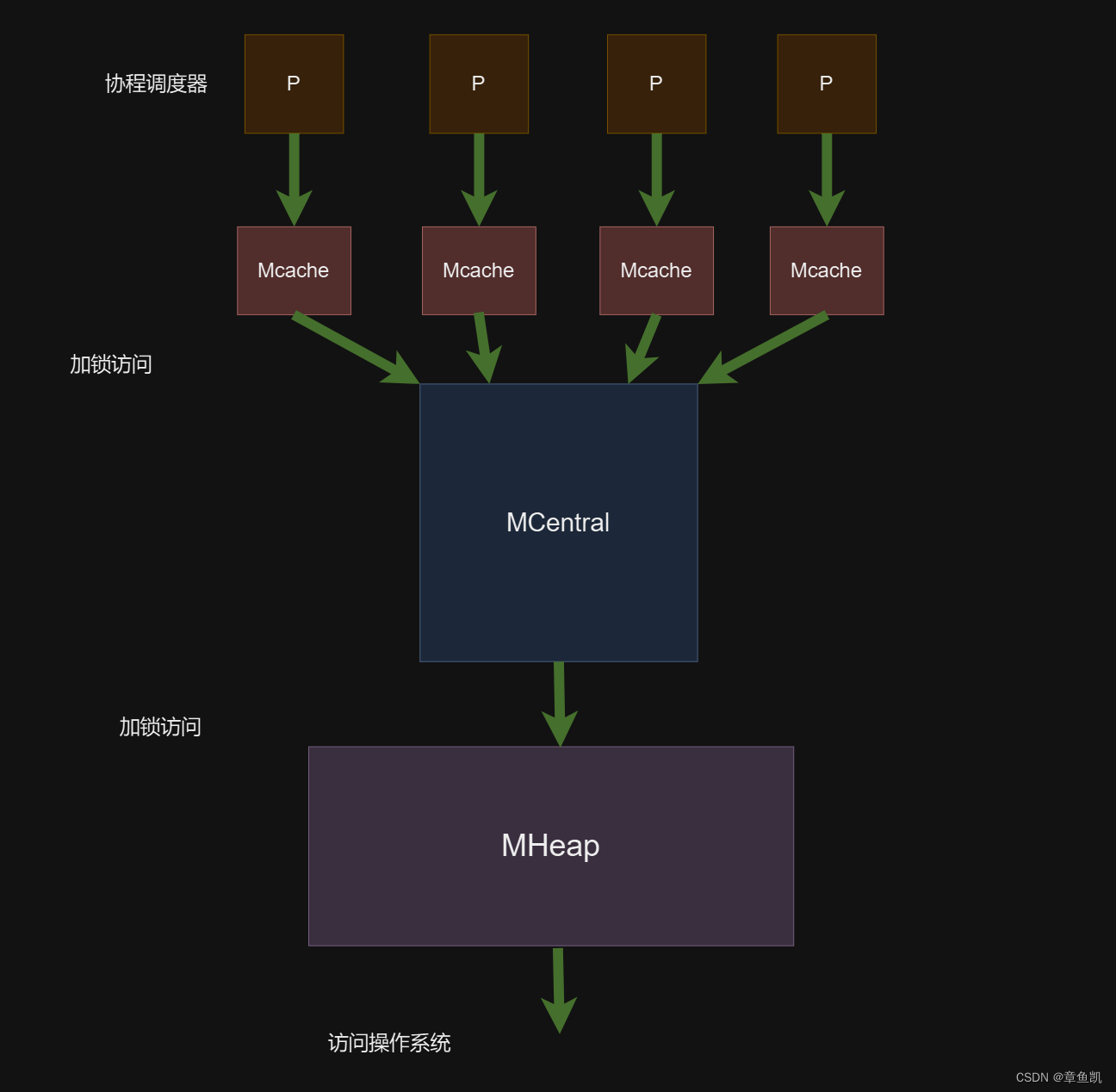
Golang的内存关系
1.Page Golang的Page,在操作系统对虚拟内存管理的MMU定义的物理页有相似的定义,默认的Page为8KB 2.mSpan 多个连续的Page称之为是一个Span,其定义含义有操作系统的管理的页表相似 3.Size Class Size Class: 相当于 一个等级和刻度, 比如 第二等级 就代表 一个Pag…...
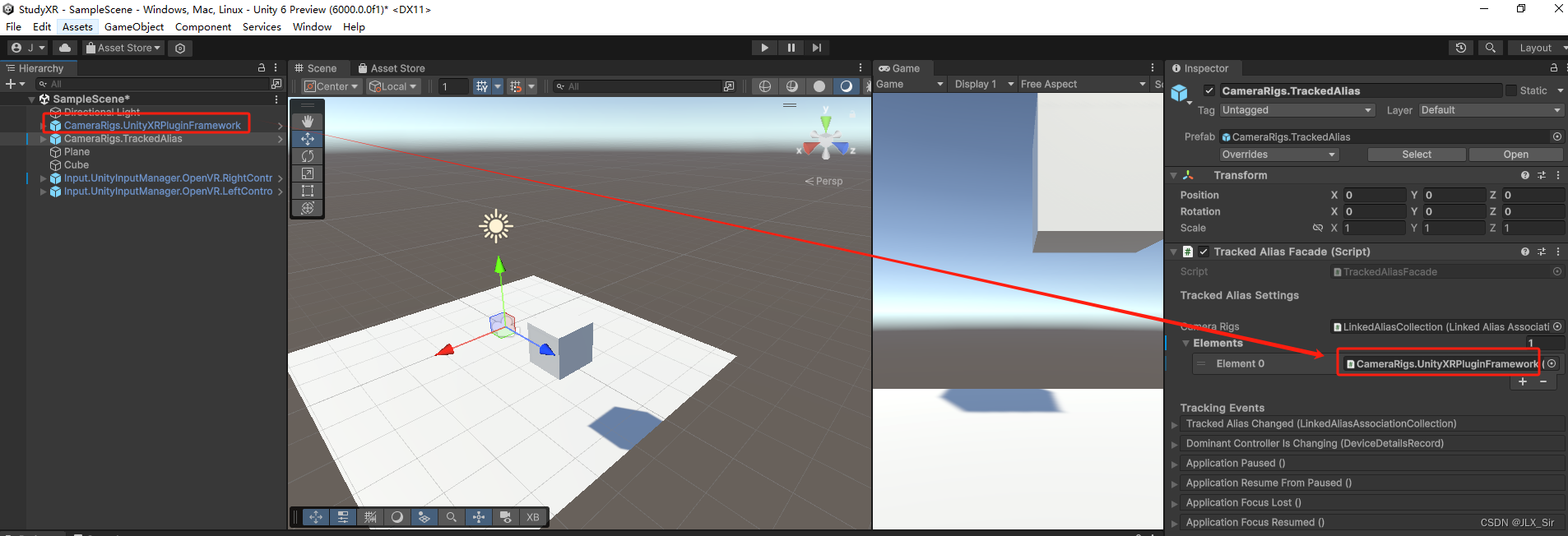
VRTK4.0学习——(二)
手柄绑定以及显示 1.导入CameraRigs.UnityXRPluginFramework 和 CameraRigs.TrackedAlias 预设,将CameraRigs.UnityXRPluginFramework拖入CameraRigs.TrackedAlias的Elements中即可,运行软件后即可看到手柄了 注:如果无法看到手柄ÿ…...

体验Photoshop:无需下载,直接在浏览器编辑图片
搜索Photoshop时,映入眼帘的是PS软件下载,自学PS软件需要多长时间,学PS软件有必要报班吗...PS软件的设计功能很多,除了常见的图像处理功能外,还涉及图形、文本、视频、出版等。不管你是平面设计师,UI/UX设计…...

Codeforces Round 895 (Div. 3)(A,B,C)题解(自己VP的,没有参加这场比赛)
A. Two Vessels 题解: 这题直接计算两个杯子之间的差值,然后直接除以2倍杯子的容量直接过,没有任何难度 #include<bits/stdc.h> using namespace std;int t; int a,b,c;int main() {cin>>t;while(t--){cin>>a>>b>…...

9秒爬取庆余年2分集剧情
版本一: 要创建一个Python爬虫程序来爬取指定网站的分集剧情,我们需要使用requests库来发送HTTP请求,以及BeautifulSoup库来解析HTML内容。以下是一个简单的示例,展示了如何爬取你提供的网站的分集剧情,并将每集剧情保存到本地的.txt文件中。 首先,确保你已经安装了req…...

阿里云布置net core 项目
一、 创建镜像 给镜像添加触发器,编译的时候会触发k8s集群里的taget链接,从而更新项目 二,创建k8s集群 使用镜像创建 添加基本信息 镜像名称:镜像仓库》基本信息公网地址镜像Tag:创建镜像时的镜像版本镜像配置为:总…...

两整数之和 ---- 位运算
题目链接 题目: 分析: 题目中要求不能使用-, 考虑到我们的位运算异或^, 是无进位加法, 可以使用如果是无进位加法, 那么我们就要找到进位, 并进行计算, 进位只有1和1相加时才会产生进位1, 而0和1相加无进位, 进位为0, 那么我们就想到了&运算, 1&1 1, 0&1 0, 所…...

长城电脑压缩文件丢失了怎么办?怎么解决
在数字化时代,电脑已成为我们日常生活和工作中不可或缺的设备。长城电脑作为国内知名品牌,以其稳定可靠的性能赢得了广大用户的信赖。然而,即便是可靠的电脑,也难免会遇到一些问题。其中,压缩文件丢失无疑是一个令人头…...

论文笔记《基于深度学习模型的药物-靶标结合亲和力预测》
基于深度学习模型的药物-靶标结合亲和力预测 这是一篇二区的文章,算是一个综述,记录一下在阅读过程中遇到的问题。 文章目录 基于深度学习模型的药物-靶标结合亲和力预测前言一、蛋白质接触图谱二、为什么蛋白质图谱的准确性对DTA模型预测结果没有影响1…...

ArrayList和LinkedList对比,ArrayList使用注意事项
ArrayList和LinkedList对比,ArrayList使用注意事项 ArrayList 和 LinkedList 是 Java 中常用的两种集合类,它们在内部实现和性能上有一些重要的区别。 ArrayList: ArrayList 是基于动态数组实现的。它内部使用一个数组来存储元素,当数组空间…...
小熊家务帮day5-day7 客户管理模块1 (小程序认证,手机验证码认证,账号密码认证,修改密码,找回密码等)
客户管理模块 1.认证模块1.1 认证方式介绍1.1.1 小程序认证1.1.2 手机验证码登录1.1.3 账号密码认证 1.2 小程序认证1.2.1 小程序申请1.2.2 创建客户后端工程jzo2o-customer1.2.3 开发部署前端1.2.4 小程序认证流程1.2.4.1 customer小程序认证接口设计Controller层Service层调用…...

计算机图形学入门02:线性代数基础
1.向量(Vetors) 向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。 向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。 1.1向量点乘(…...
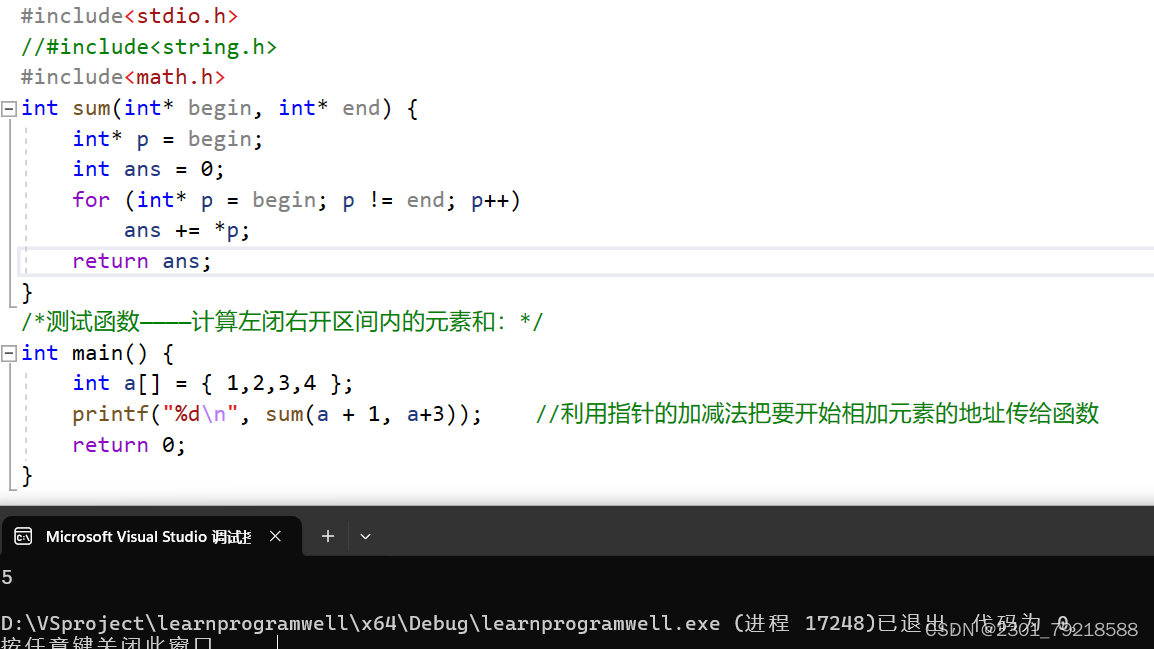
函数:计算数组的元素和
一、计算数组的元素和 参数传递给函数时,实际上只有数组的首地址作为指针传递给了函数。 在函数定义中的int a[ ]等价于int *a。在只有地址信息的情况下,是无法知道数组里有多少个元素的,因此在计算数组中的元素和时,要加一个参…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
