计算机组成原理·存储系统疑点归纳
组原这门课有点学得不是很懂,现在快考试了,挑几个做错了的题分析、记录一下。
N o . 1 \mathit{No}.1 No.1 x x x、 y y y 为定点整数,其格式为 1 1 1 位符号位、 n n n 位数值位,若采用补码一位乘法实现乘法运算,则最多需要_______次加法运算。
A. n − 1 n-1 n−1
B. n n n
C. n + 1 n+1 n+1
D. n + 2 n+2 n+2
答案 C
总结一下原码一位乘法、补码一位乘法中,到底进行了多少次移位和多少次加法。
首先来看原码一位乘法:
原码一位乘法中,加法的次数等于移位的次数。可以看到,如果原数据包含符号位一共有 k k k 位,那么最后移位到只剩下符号位,即移位 k − 1 k-1 k−1 次,加法 k − 1 k-1 k−1 次。
再来看补码一位乘法:
补码一位乘法中,加法比移位多进行 1 1 1 次。如果原数据包含符号位一共有 k k k 位,那么会先在后面加一位“0”得到 k + 1 k+1 k+1 位的“乘数”参与运算。最后移到只剩下 2 2 2 位,即移位 k − 1 k-1 k−1 次,加法 k k k 次。
将上述结果列成下表:
乘法类型 数据位数(包括符号位) 移位次数 加法次数 原码一位乘法 k k k k − 1 k-1 k−1 k − 1 k-1 k−1 补码一位乘法 k k k k − 1 k-1 k−1 k k k 套用上表的结果,此题属于补码一位乘法,且 k = n + 1 k=n+1 k=n+1,因此加法次数为 k = n + 1 k=n+1 k=n+1。
N o . 2 \mathit{No}.2 No.2 某容量为 256 M B 256\mathrm{\ MB} 256 MB 的存储器由若干 4 M × 8 \mathrm{4M\times8} 4M×8 位的 DRAM 芯片构成,该 DRAM 芯片的地址引脚和数据引脚总数是______。
A. 19 19 19
B. 22 22 22
C. 30 30 30
D. 36 36 36
答案 A
此题容易误选 C。该 DRAM 芯片的数据引脚数肯定是 8 8 8,但是地址引脚数是 11 11 11。因为 DRAM 采用的地址复用技术,分两次将行地址( 11 11 11 位)与列地址( 11 11 11 位)送入芯片中。如果是 SRAM,就需要有 22 22 22 个地址引脚。
N o . 3 \mathit{No}.3 No.3 假定用若干个 2 K × 4 2\mathrm K×4 2K×4 位的芯片组成一个 8 K × 8 8\rm K×8 8K×8 位的存储器,则地址 0 B 1 F H \rm{0B1FH} 0B1FH 所在芯片的最小地址是______。
A. 0000 H \rm{0000H} 0000H
B. 0600 H \rm{0600H} 0600H
C. 0700 H \rm{0700H} 0700H
D. 0800 H \rm{0800H} 0800H
答案 D
这个题首先值得一提的 8 K × 8 \rm{8K}\times 8 8K×8,它表示存储器有 8 K 8\rm K 8K 个存储单元,每个单元有 8 8 8 位(当初就是这里没弄懂),相当于是按字节编址了。可以在脑海里构想一下芯片的组织方式,首先是 2 2 2 个 2 K × 4 2\rm K\times 4 2K×4 的芯片位拓展为 2 K × 8 2\rm K\times 8 2K×8,然后用 4 4 4 个拓展后的芯片来进行字拓展。这 4 4 4 个拓展芯片就将存储器地址分为了四个部分:
存储器地址 位于第几个拓展芯片( 2 K × 8 2\rm K\times 8 2K×8 芯片) 0000 H ∼ 07 F F H \rm{0000H\sim 07FFH} 0000H∼07FFH 0 0 0 0800 H ∼ 0 F F F H \rm{0800H\sim 0FFFH} 0800H∼0FFFH 1 1 1 1000 H ∼ 17 F F H \rm{1000H\sim 17FFH} 1000H∼17FFH 2 2 2 1800 H ∼ 1 F F F H \rm{1800H\sim 1FFFH} 1800H∼1FFFH 3 3 3 自然, 0 B 1 F H \rm{0B1FH} 0B1FH 位于第 1 1 1 个拓展芯片内,该芯片的最小地址是 0800 H \rm{0800H} 0800H。
N o . 4 \mathit{No}.4 No.4 假定 DRAM 芯片中存储阵列的行数为 r r r、列数为 c c c,对于一个 2K×1 位的 DRAM 芯片,为保证其地址引脚数最少,并尽量减少刷新开销,则 r r r、 c c c 的取值分别是______。
A. 2048 2048 2048、 1 1 1
B. 64 64 64、 32 32 32
C. 32 32 32、 64 64 64
D. 1 1 1、 2048 2048 2048
答案 C
这个题当初是不会做,主要是涉及到一个考点,那就是 DRAM 因为电容容易漏电需要定期刷新数据,且刷新方式为按行刷新。因此减少刷新开销就是降低 r r r 的值。
N o . 5 \mathit{No}.5 No.5 下列关于缺页处理的叙述中,错误的是______。
A. 缺页是在地址转换时 CPU 检测到的一种异常
B. 缺页处理由操作系统提供的缺页处理程序完成
C. 缺页处理程序根据页故障地址从外存读入所缺失的页
D. 缺页处理完成后执行发生缺页的指令的下一条指令
答案 D
缺页处理完成后,缺页处理程序返回到原来的进程,驱使引起缺页的程序重新启动。所以是重新执行发生缺页的指令,而不是执行它的下一条指令。
N o . 6 \mathit{No}.6 No.6 下列选项中,属于指令集体系结构(ISA)规定的内容是______。
I.指令字格式和指令类型
II.CPU的时钟周期
Ⅲ.通用寄存器个数和位数
IV.加法器的进位方式
A. 仅I、II
B. 仅I、II、Ⅲ
C. 仅Ⅱ、IV
D. 仅I、Ⅲ、IV
答案 B
加法器的进位方式,如是串行加法器还是并行加法器,是属于微架构(Microarchitecture)的内容。但是也有说 CPU 的时钟周期是微架构规定的,见这篇文章,这个确实有争议。不过I、Ⅲ毫无疑问是 ISA 的范畴。
N o . 7 \mathit{No}.7 No.7 二维交叉奇偶校验编码不能全部检测以下哪种出错?
A. 2 2 2 位错
B. 3 3 3 位错
C. 4 4 4 位错
D. 5 5 5 位错
E. 6 6 6 位错
答案 CE
当初没有想到 6 6 6 位错会有哪些漏网之鱼,后面通过问老师得知下面这种 6 6 6 位错就能够逃脱检测:
[ ⋮ ⋮ ⋮ ⋯ D D D ⋯ ⋯ D D D ⋯ ⋯ D D D ⋯ ⋮ ⋮ ⋮ ] \begin{bmatrix}&\vdots&\vdots&\vdots\\ \cdots&\red{D}&\red D& D&\cdots\\ \cdots&\red D& D& \red D&\cdots\\ \cdots&D&\red D&\red D&\cdots\\ &\vdots&\vdots&\vdots\end{bmatrix} ⋯⋯⋯⋮DDD⋮⋮DDD⋮⋮DDD⋮⋯⋯⋯ D D D 表示正常数据, D \red D D 表示出错的数据。这种情况下,每行每列的校验码都检测不出错误。实际上,二维交叉奇偶校验码不能全部检测的错误是除了 2 2 2 位错之外的所有偶数位错。
相关文章:

计算机组成原理·存储系统疑点归纳
组原这门课有点学得不是很懂,现在快考试了,挑几个做错了的题分析、记录一下。 N o . 1 \mathit{No}.1 No.1 x x x、 y y y 为定点整数,其格式为 1 1 1 位符号位、 n n n 位数值位,若采用补码一位乘法实现乘法运算,则…...

在 GPU 上实现全规模文件系统加速
摘要 现代高性能计算和人工智能计算解决方案经常使用 GPU 作为其主要计算能力来源。这就为 GPU 应用程序的存储操作造成了严重的不平衡,因为每一个此类存储操作都必须向 CPU 发出信号并由 CPU 处理。在 GPU4FS 中,我们针对这种不平衡提出了一个彻底的解决…...

代码随想录算法训练营Day7|454.四数相加II、 383. 赎金信、15. 三数之和、 18. 四数之和
454.四数相加II 四个数组分成两组进行for循环,先用HashMap存储所有第一组for循环出现的和的次数。再进行第二组for循环,每一次得出的和判断其负数是否在map的key中,如果存在,就加上这个value。 class Solution {public int four…...

编译器屏障概述
文章目录 1. 前言2. 编译器内存屏障2.1 编译器内存访问重排序规则2.2 编译器屏障的几种形式2.2.1 显式编译器屏障2.2.2 隐式编译器屏障2.2.3 硬件内存屏障充当编译屏障2.2.4 编程语言内存模型提供的编译屏障 2.3 编译器内存屏障实例2.3.1 Linux spinlock 3. 结语4. 参考资料 1.…...

RUST宏编程入门
宏指示符 在Rust的宏编程中,宏可以接受多种类型的参数,称为“指示符”。这些指示符帮助宏识别不同类型的代码片段,并相应地处理它们。 这里列出全部指示符: blockexpr 用于表达式ident 用于变量名或函数名itemliteral 用于字面常…...
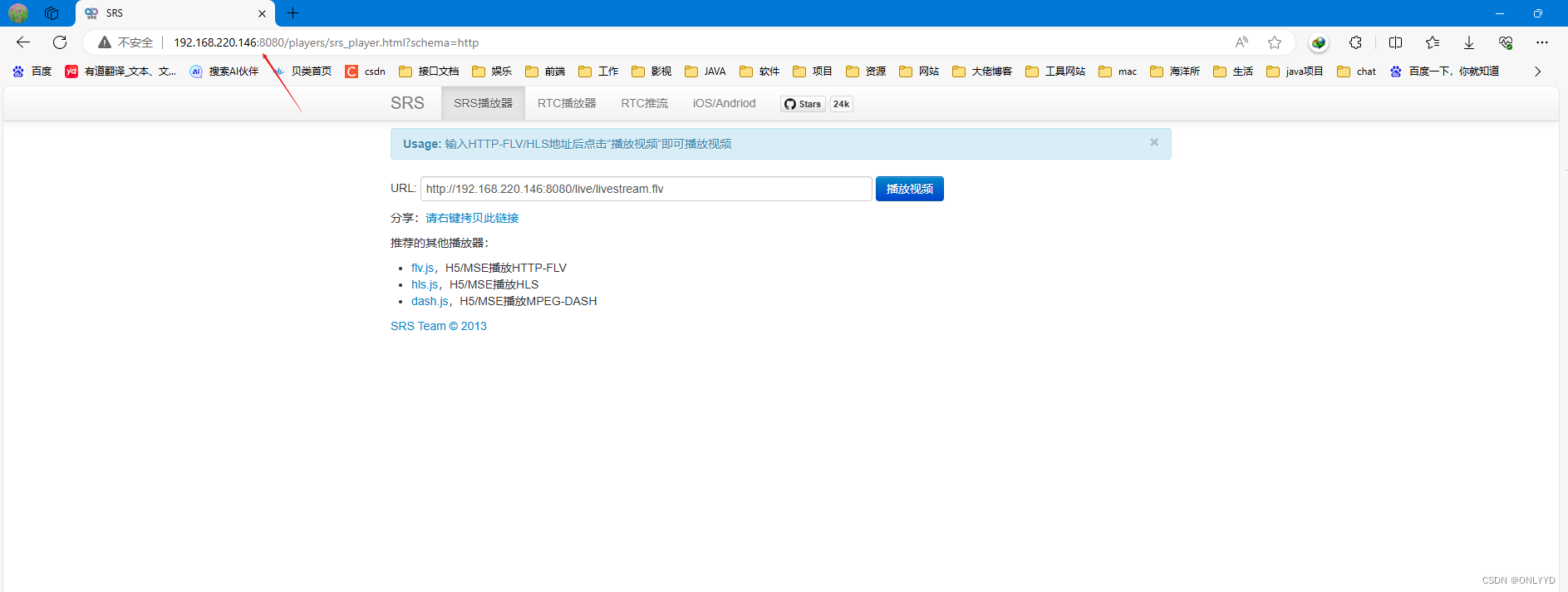
linux安装srs
获取srs cd /opt git clone -b 4.0release https://gitee.com/ossrs/srs.git cd srs/trunk 启动srs ./objs/srs -c conf/srs.conf ./etc/init.d/srs status 访问http://192.168.220.146:8080/出现下方图片说明安装成功 点击进入SRS控制台看到下方图片...
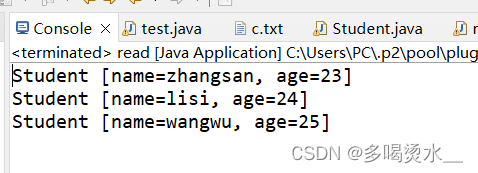
IO流(2)
缓冲流 字节缓冲流 利用字节缓冲区拷贝文件,一次读取一个字节: public class test {public static void main(String [] args) throws IOException {//利用字节缓冲区来拷贝文件BufferedInputStream bisnew BufferedInputStream(new FileInputStream(&…...

【docker】docker启动bitnami/mysql
说明:-v 宿主机目录:docker容器目录,-p 同理 注意:/opt/bitnami/mysql/conf/bitnami 目录自定义conf的目录,不能使用原有的/opt/bitnami/mysql/conf 目录。 容器启动后可在宿主机的/宿主/mysql8.0/conf,添加my_custom.…...

边缘计算、云计算、雾计算在物联网中的作用
边缘计算和雾计算不像云那样广为人知,但可以为企业和物联网公司提供很多帮助。这些网络解决了物联网云计算服务无法解决的许多问题,并使分散的数据存储适应特定的需求。让我们分别研究一下边缘计算、雾计算和云计算的优势。 雾计算的好处 低延迟。雾网络…...

【c语言】探索内存函数
探索内存函数 memcpy函数memmove函数memset函数memcmp函数: memcpy函数 memcpy函数声明: void * memcpy ( void * destination, const void * source, size_t num );将source空间下的num个字符复制到dest中去 函数的使用: 将字符数组a的5字…...

day46 完全背包理论基础 518. 零钱兑换 II 377. 组合总和 Ⅳ
完全背包理论基础 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 01背包内嵌的循环是从…...
【linux】运维-基础知识-认知hahoop周边
1. HDFS HDFS(Hadoop Distributed File System)–Hadoop分布式文件存储系统 源自于Google的GFS论文,HDFS是GFS的克隆版 HDFS是Hadoop中数据存储和管理的基础 他是一个高容错的系统,能够自动解决硬件故障,eg:…...
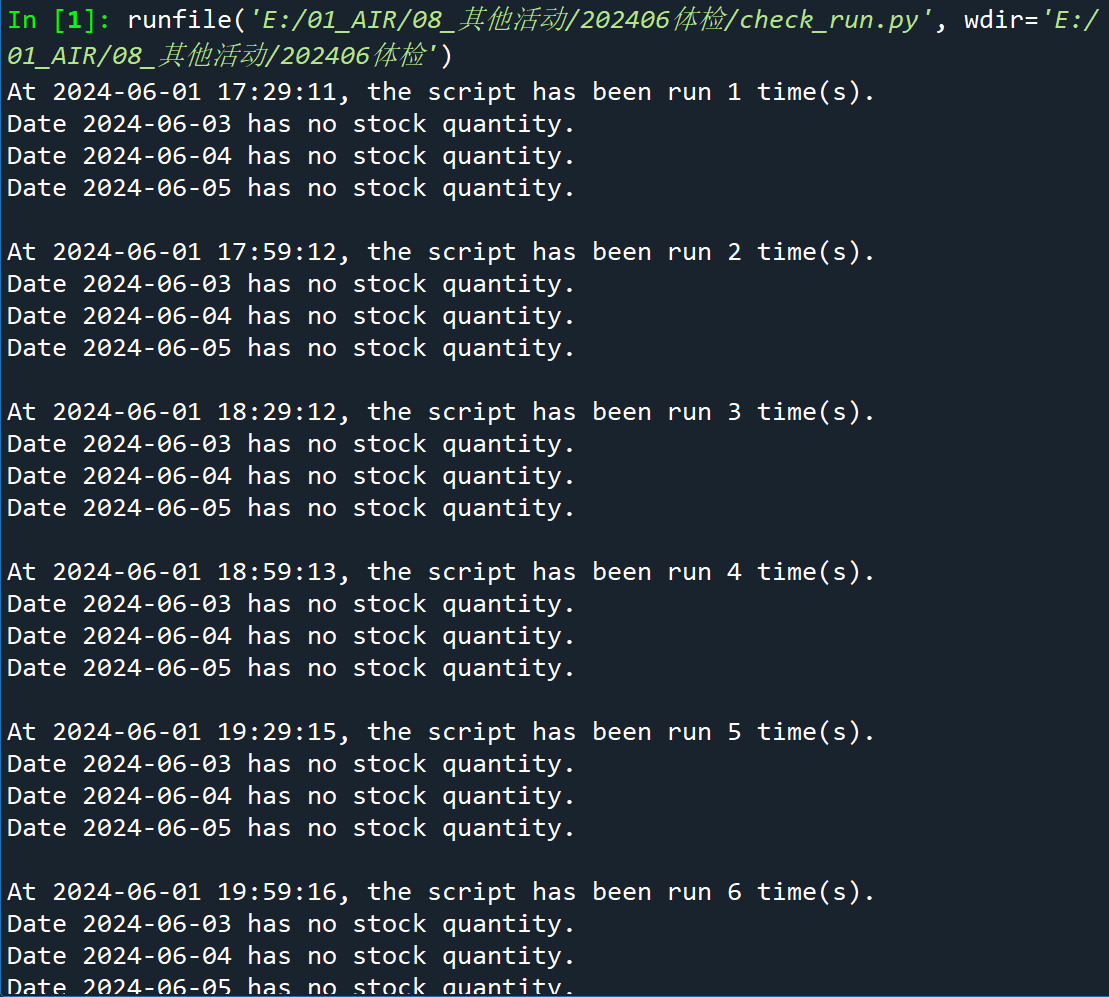
Python自动实时查询预约网站的剩余名额并在有余额时发邮件提示
本文介绍基于Python语言,自动、定时监测某体检预约网站中指定日期的体检余额,并在有体检余额时自动给自己发送邮件提醒的方法。 来到春招末期,很多单位进入了体检流程。其中,银行(尤其是四大行)喜欢“海检”…...
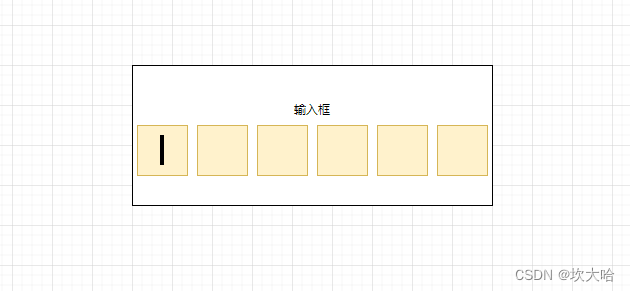
Flutter 验证码输入框
前言: 验证码输入框很常见:处理不好 bug也会比较多 想实现方法很多,这里列举一种完美方式,完美兼容 软键盘粘贴方式 效果如下: 之前使用 uniapp 的方式实现过一次 两种方式(原理相同)࿱…...

如何从0到设计一个CRM系统
什么是CRM 设计开始之前,先来了解一下什么是CRM。CRM(Customer Relationship Management)是指通过建立和维护与客户的良好关系,达到满足客户需求、提高客户满意度、增加业务收入的一种管理方法和策略。CRM涉及到跟踪和管理客户的所…...
Numba 的 CUDA 示例 (2/4):穿针引线
本教程为 Numba CUDA 示例 第 2 部分。 按照本系列从头开始使用 Python 学习 CUDA 编程 介绍 在本系列的第一部分中,我们讨论了如何使用 GPU 运行高度并行算法。高度并行任务是指任务完全相互独立的任务,例如对两个数组求和或应用任何元素函数。 在本教…...

项目的各个阶段如何编写标准的Git commit消息
标准提交消息格式 一个标准的提交消息应包括三部分:标题(summary)、正文(description)和脚注(footer)。 1. 标题(Summary) 简洁明了,不超过50个字符。使用…...
Python课设-学生信息管理系统
一、效果展示图 二、前端代码 1、HTML代码 <1>index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">…...

openssl 常用命令demo
RSA Private Key的结构(ASN.1) RSAPrivateKey :: SEQUENCE { version Version, modulus INTEGER, -- n publicExponent INTEGER, -- e privateExponent INTEGER, -- d prime1 INTEGER, -- …...

【Linux】Linux基本指令2
目录 1.man指令(重要): 2.echo指令 3.cp指令(重要): 4.mv指令 5.cat指令/echo指令重定向 6.more指令 7.less指令(重要) 8.head指令 9.tail指令 我们接着上一篇:h…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
