数据结构(C):从初识堆到堆排序的实现


目录
🌞0.前言
🚈 1.堆的概念
🚈 2.堆的实现
🚝2.1堆向下调整算法
🚝2.2堆的创建(堆向下调整算法)
✈️2.2.1 向下调整建堆时间复杂度
🚝2.3堆向上调整算法
🚝2.4堆的创建(堆向上调整算法)
✈️2.4.1向上调整算法建堆的时间复杂度
🚝2.5堆的插入
🚝2.6堆的删除
🚝2.7建堆的代码实现
✈️2.7.1向下调整实现堆的建立
✈️2.7.2向上调整实现堆的建立
🚈 3.完整的堆的代码的实现
🚝3.1堆的创建
🚝3.2堆的销毁
🚝3.3堆的插入
🚝3.4堆的删除(头删)
🚝3.5取堆顶元素的数据
🚝3.6 堆的数据个数
🚝3.7堆的判空
🚈 4.堆的应用堆排序
✍5.结束语
🌞0.前言
言C之言,聊C之识,以C会友,共向远方。各位博友的各位你们好啊,这里是持续分享数据结构知识的小赵同学,今天要分享的数据结构知识是堆,在这一章,小赵将会向大家展开聊聊堆的相关知识。✊
🚈 1.堆的概念
堆就是以 二叉树的顺序存储方式来存储元素,同时又要满足 父亲结点存储数据都要大于等于儿子结点存储数据(也可以是父亲结点数据都要小于等于儿子结点数据)的一种数据结构。堆只有两种即大堆和小堆,大堆就是父亲结点数据大于等于儿子结点数据,小堆则反之。
同时这里要注意的是堆一定是完全二叉树,不然就不是堆。那完全二叉树是什么呢?这个地方不懂的博友可以看我们的这一篇博客:数据结构(C)树的概念和二叉树初见http://t.csdnimg.cn/JnWfb
如果看完了还是不明白可以私信小赵询问哦。
好了下面让我们看看上面说的两种堆在图上是怎么呈现的呢?
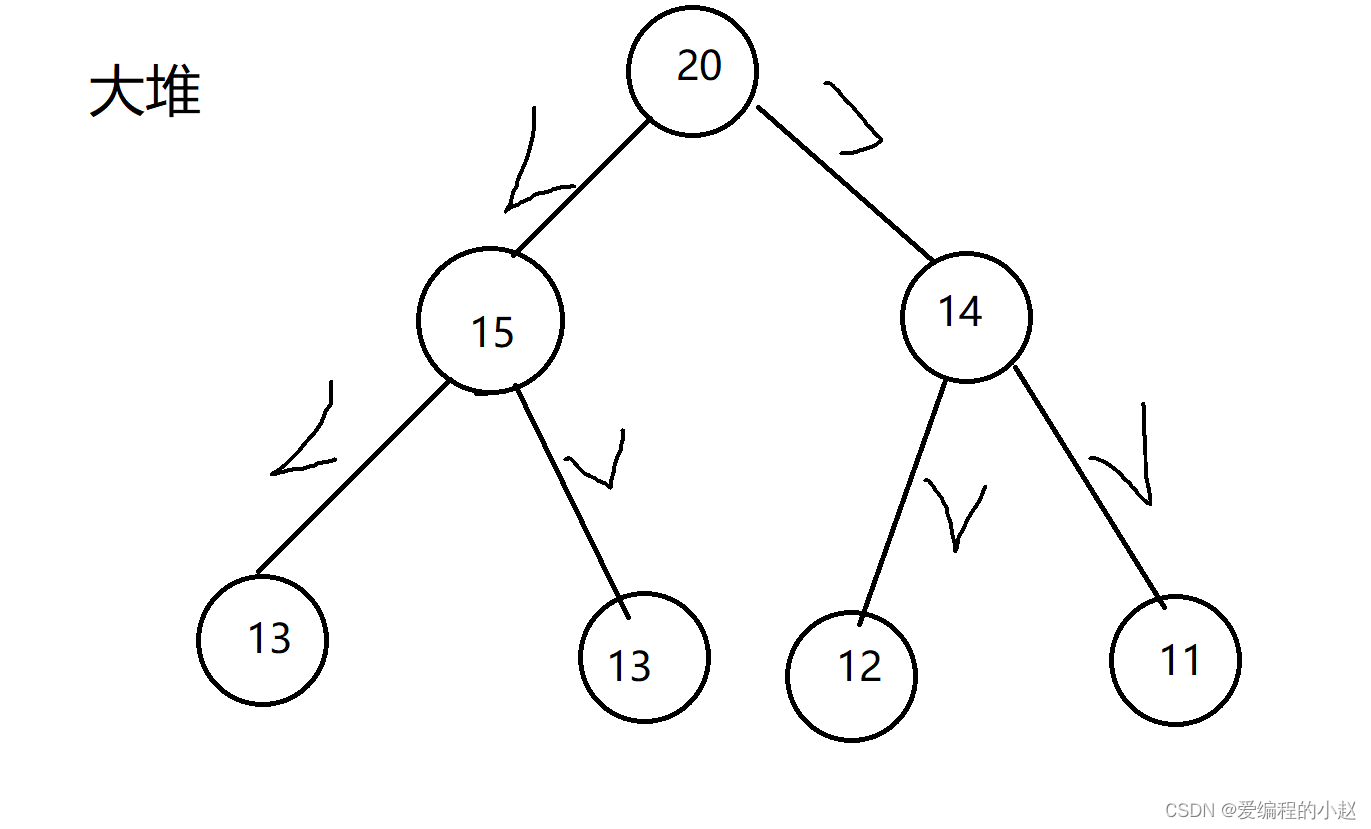
我们发现我们的任意一个父节点都比他的两个子节点大(或等于)这个时候这就是一个大堆。
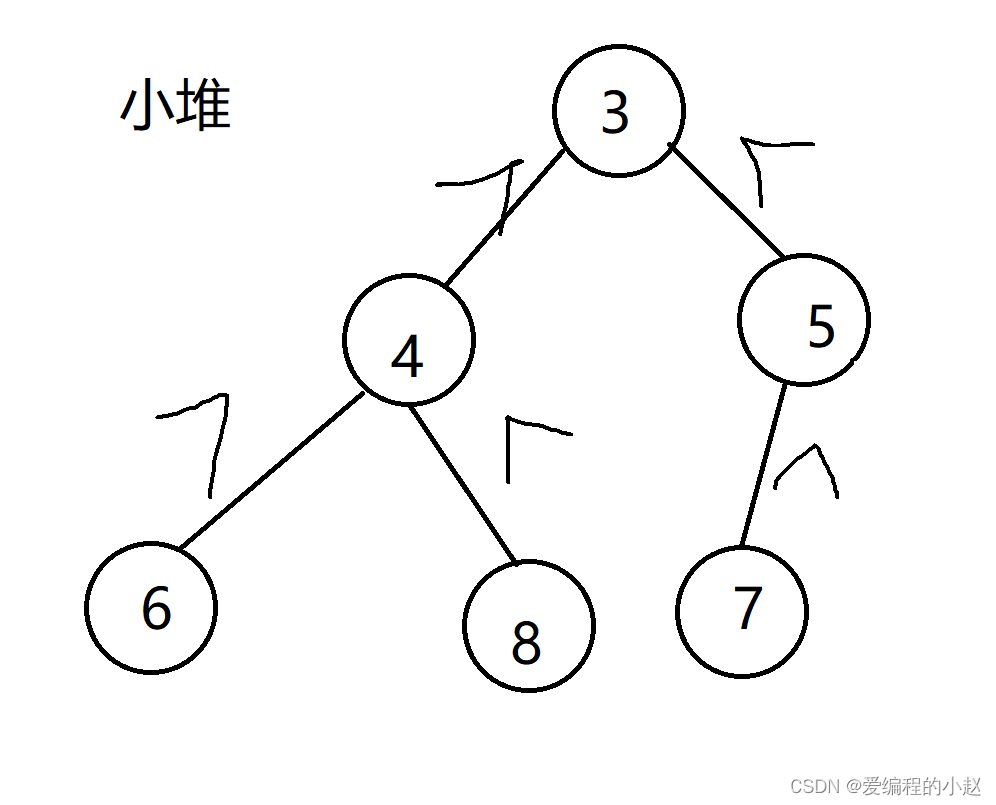
我们发现我们的任意一个父节点都比他的两个子节点小(或等于)这个时候这就是一个小堆。
虽然堆是完全二叉树,但其的存储方式却与二叉树不同,我们一般存储堆的方式是数组。而我们上面所画的叫逻辑结构,那怎么由数组的存储方式,转化为我们的逻辑结构呢?
我们在介绍二叉树的时候其实也曾简单的说过二叉树是有顺序的,是从上到下,从左向右的,按这个顺序我们就可以给我们的二叉树标序号。
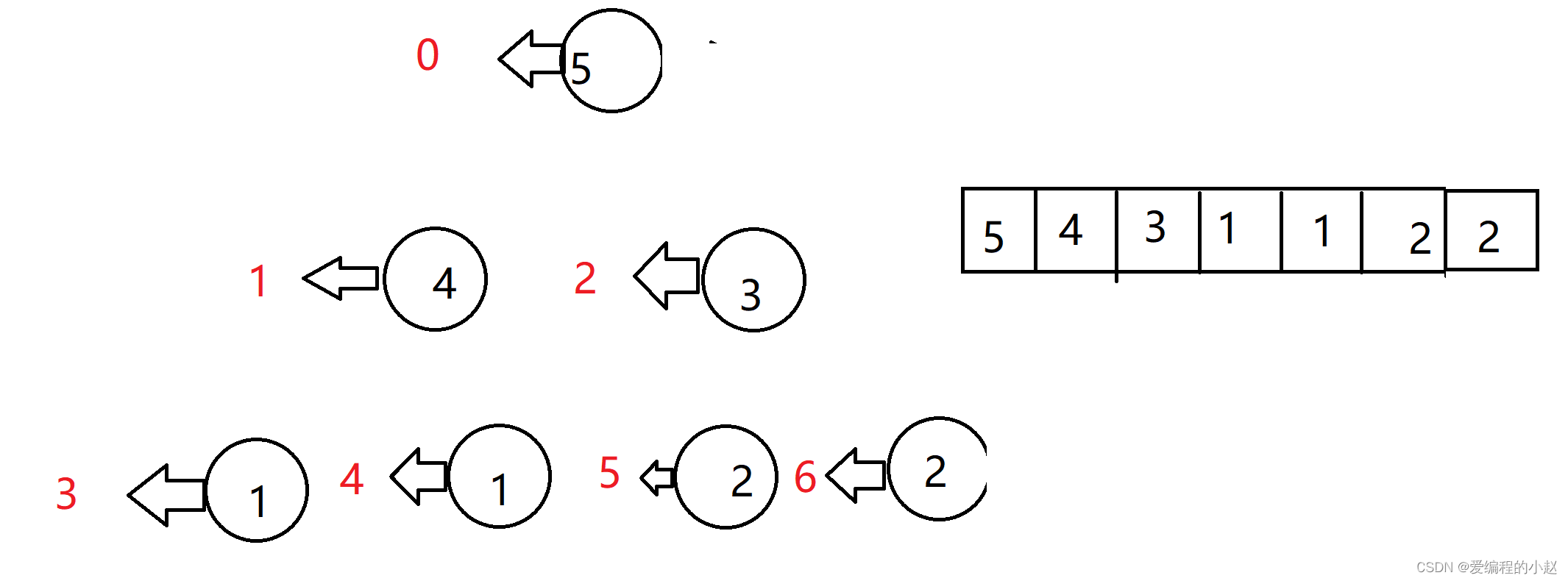
那么就可以我们的逻辑结构转化成我们的数组结构了,既然我们已经会将逻辑结构转化为数组结构了,那么将数组结构转化为逻辑结构也就没有这么难了,大家可以自己试试,如果实在实现不了也可以找小赵咨询哦。
🚈 2.堆的实现
🚝2.1堆向下调整算法
什么是向下调整算法呢?其实正如其名就是从上到下调整堆的意思。要想更深入了解这个东西就先来看这张图。
看这张图这是一个很明显的小堆对吧,那我这个时候要你改成一个大堆怎么办,这个时候的操作其实是2,3进行比较,然后拿出大的和1换这个就成大堆了。
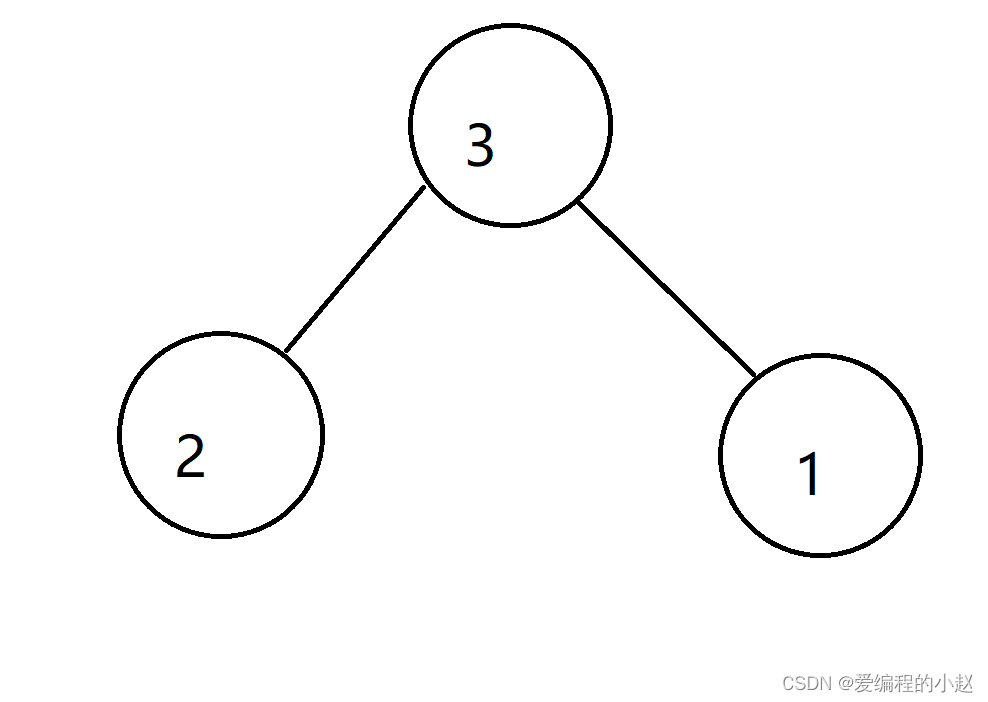
可如果这个时候我给你的是个这样的堆你又该怎么办(要改成小堆)
其实这个时候也是可以操作的,因为下面是有序的堆,我们只需要按照前面的顺序一步步来就可以完成了。只不过这个时候改成了选择两个子中的小的哪一个,因为我们要做得是小堆(这个时候之所以说他下面是有序的堆是因为盖住最上面的一个,下面的两个堆都是小堆,我们要改成的也是小堆。)
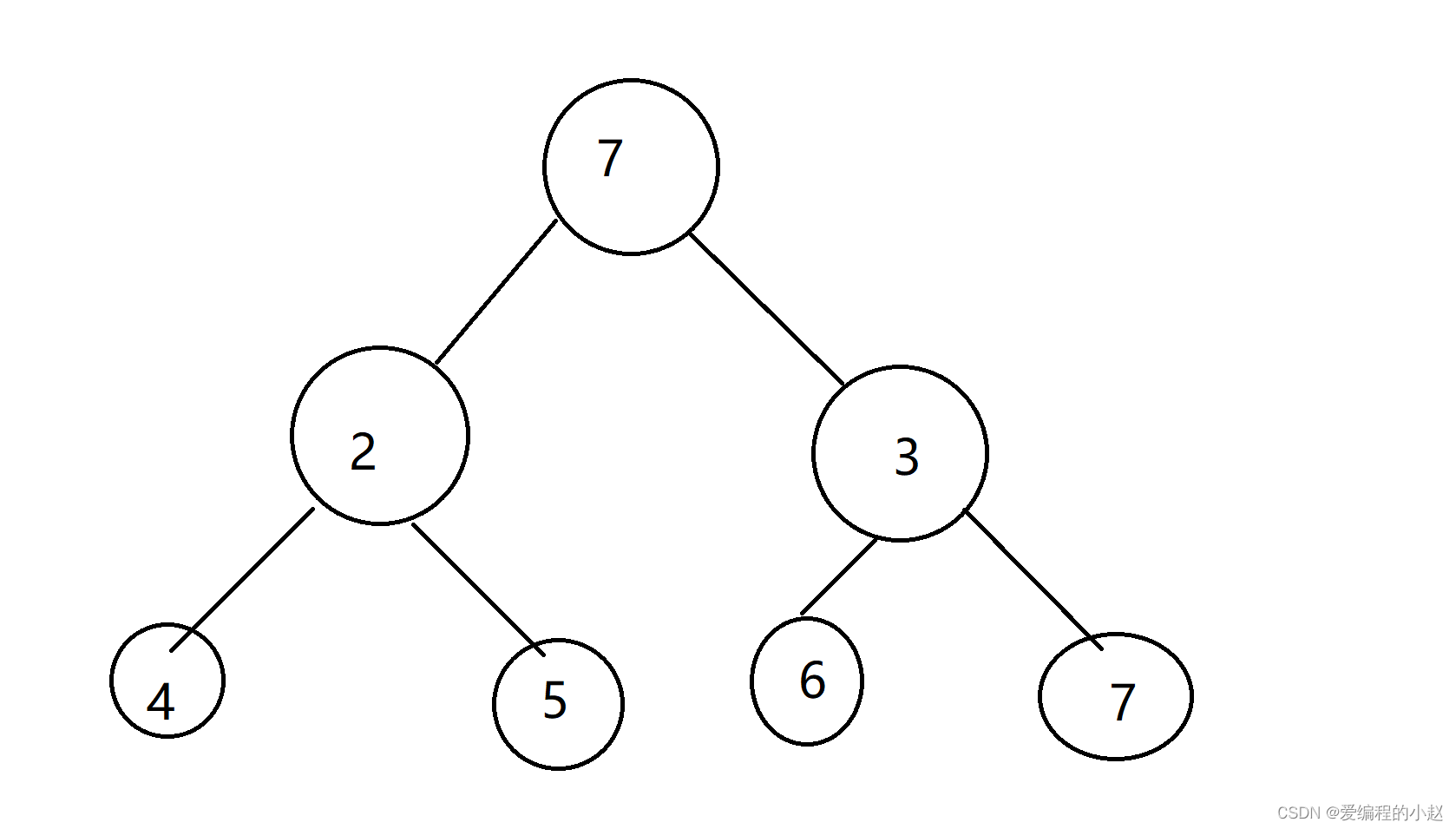
那如果是无序的呢? (改成小堆)

这个时候我们发现我们再想把这个改成小堆的难度就很大了。
🚝2.2堆的创建(堆向下调整算法)
那通过上面的实验我们发现,想通过一个位置来做上面的操作,并把整个堆都变成小(大)堆,必须下面就是一个小(大)堆。所以我们的向下调整其实也是从最下面的开始的,而且我们刚刚做的步骤其实就是向下调整。
那么再面对上面那个无序的堆我们也就有方法了。
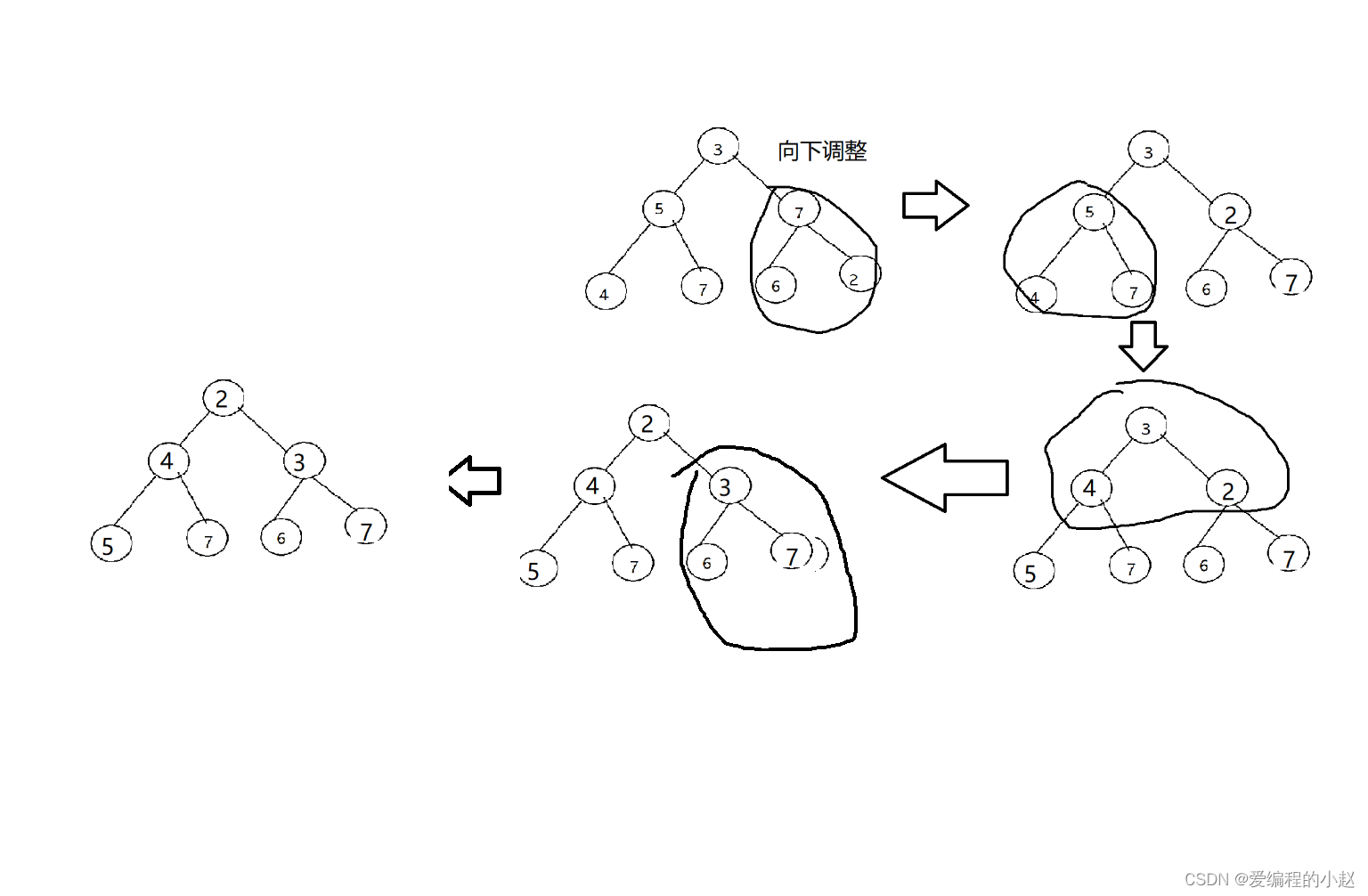
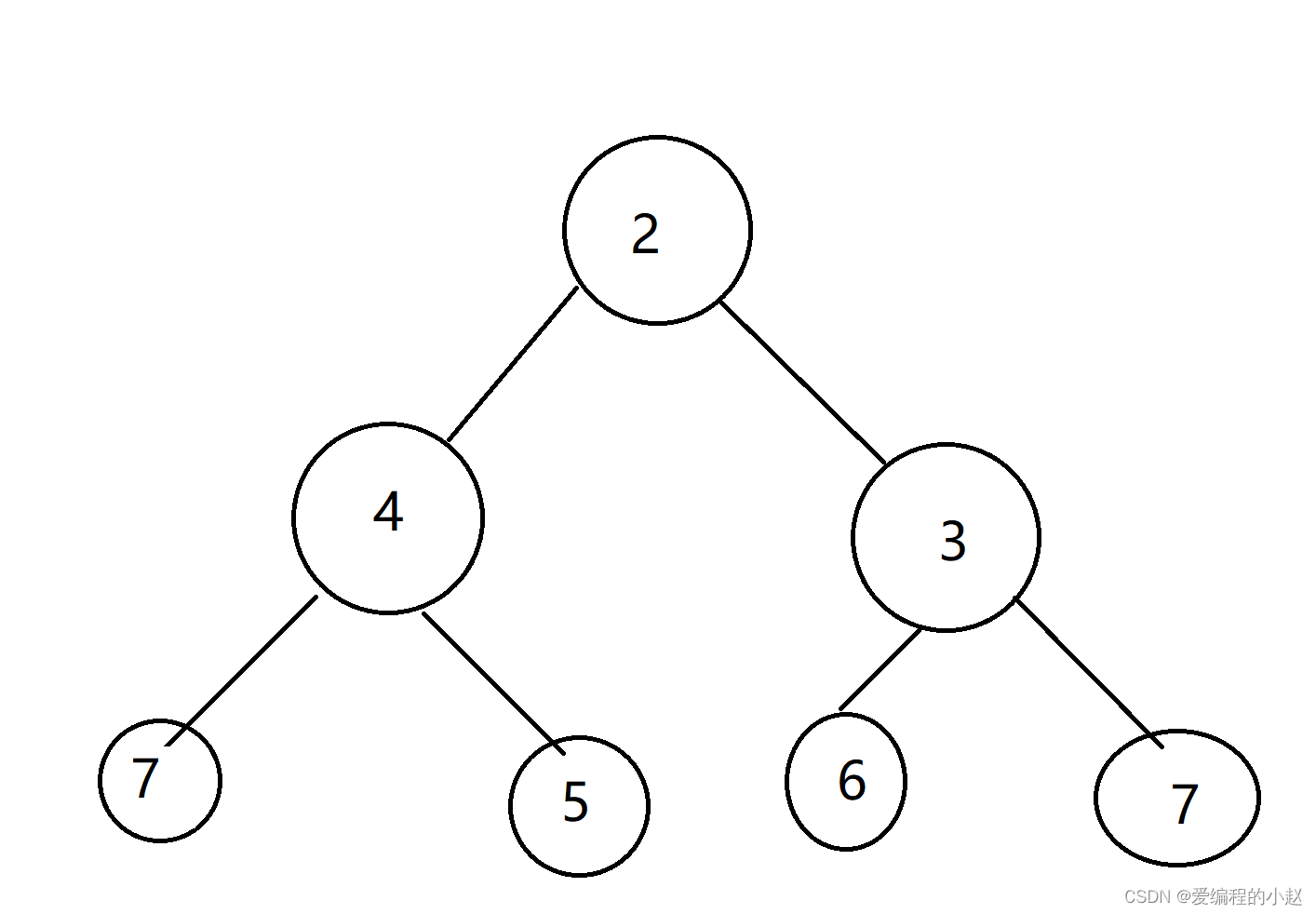
这个时候我们就可以做到将无序的堆转化成有序的堆了。 那么这个时候我们面对任何一个无序的数组,都可以通过这样的方式将他转化成堆.(至少在逻辑图上可以实现,代码实现下面说)
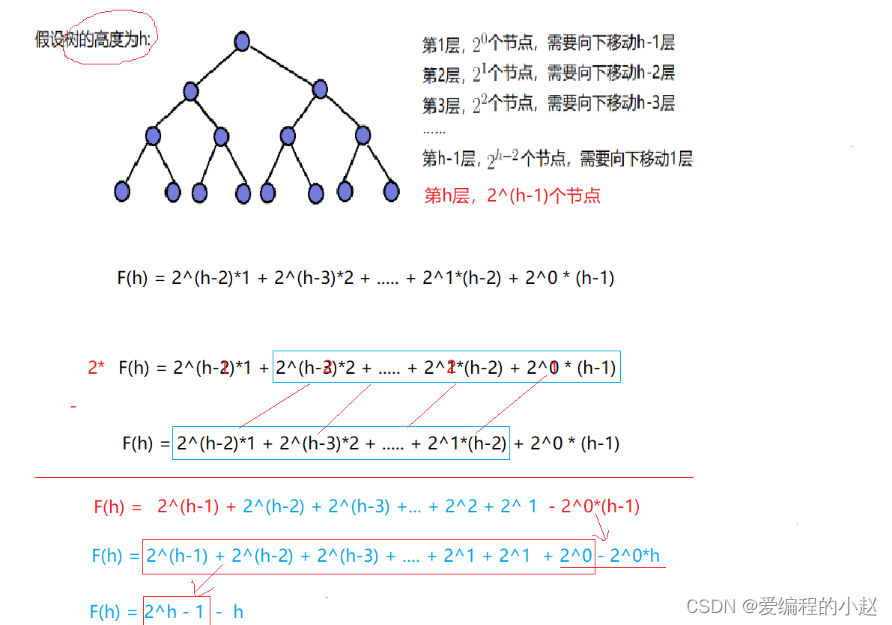
✈️2.2.1 向下调整建堆时间复杂度
每层节点个数 × 最坏情况向下调整次数:
T(N) = 2^(h-2) × 1 + 2^(h-3) × 2 + … … + 2^1 × (h-2)+2^0*(h-1)
错位相减法
等号左右两边乘个 2 得到一个新公式,再用新公式减去旧的公式,具体见下图
🚝2.3堆向上调整算法
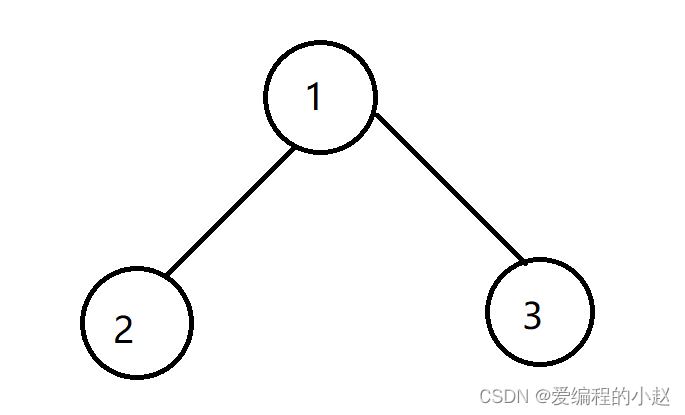
聊了向下调整算法,那么其实也有向上调整算法。
如这里我们如何把这个堆改成大堆
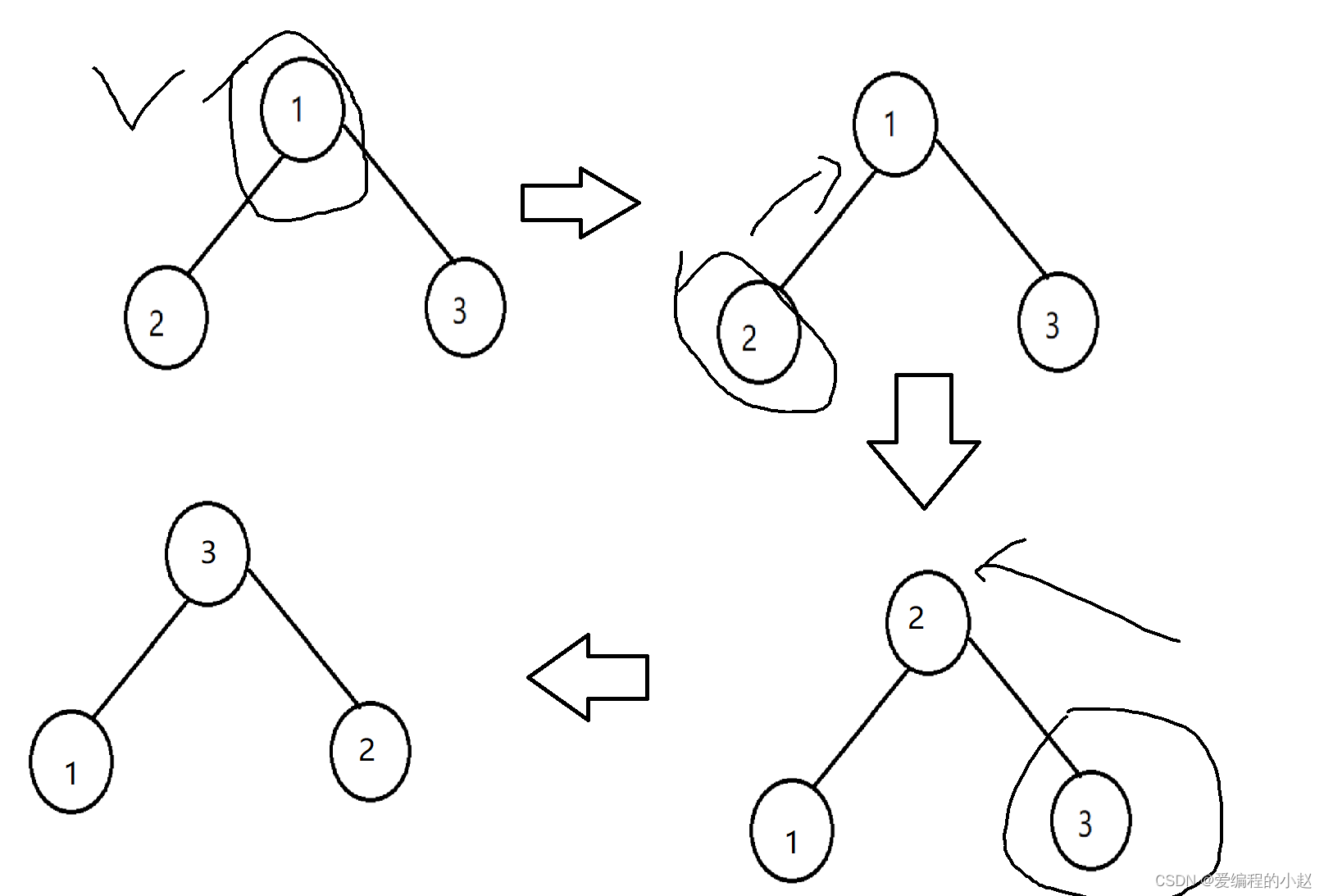
向上调整一般是怎么玩的呢,一般我们的向上调整法就是从下面往上调整,向这里要想调整到我们想要的样子就要三步
🚝2.4堆的创建(堆向上调整算法)
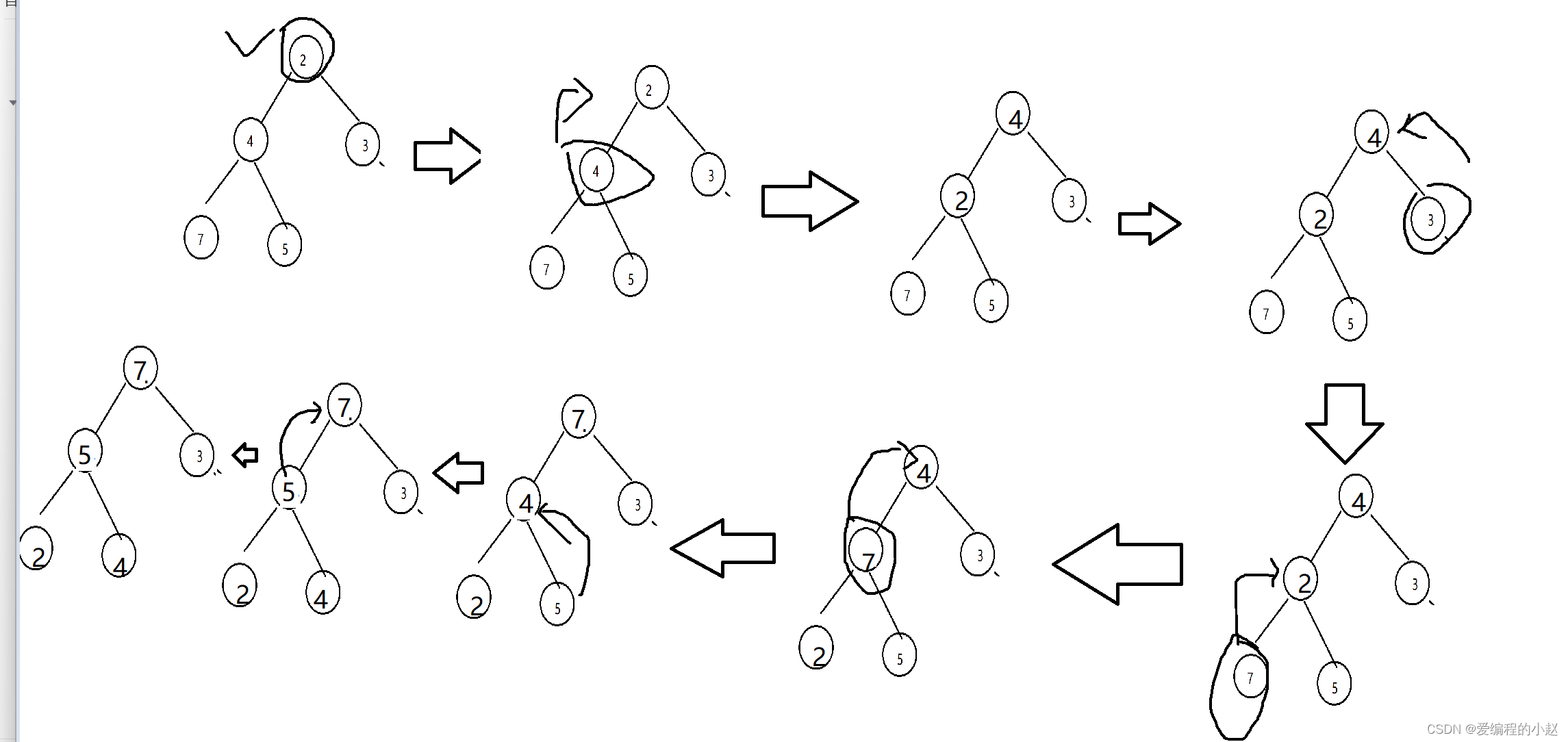
这里呢也和上面一样,向上调整的地方的上面必须是已经调整好的,所以我们一般用向上调整法去建堆的时候往往要从第一个开始建堆到最下面。
✈️2.4.1向上调整算法建堆的时间复杂度
T(N) = 2^1× 1 + 2^2× 2 + 2^3 ×3+ … … + 2^(h-3)× (h-3) + 2^(h-2) × (h-2)+ 2^(h-1) × (h-1)
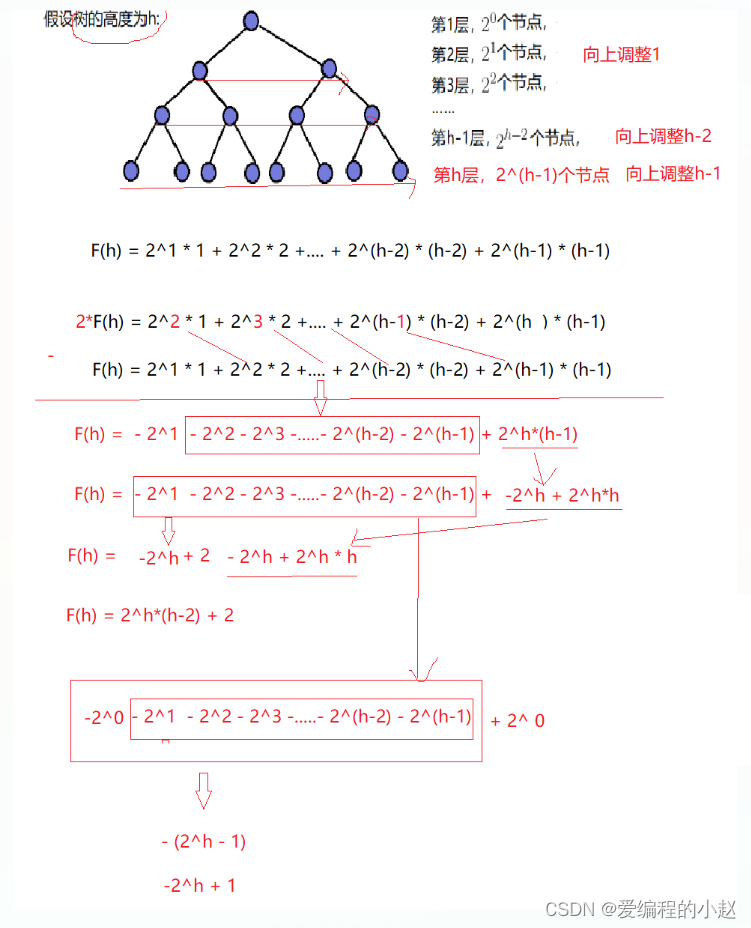
综上:向下调整建堆要更优秀,效率更高
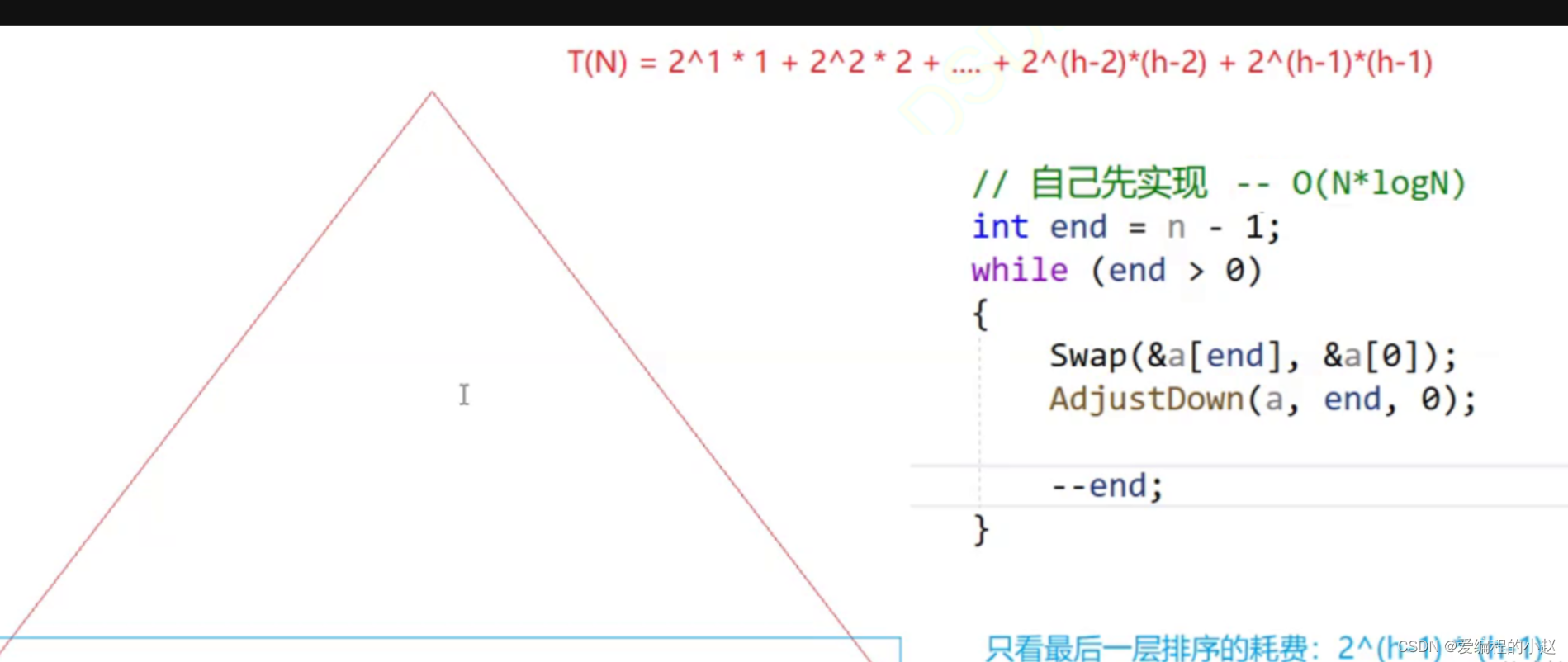
但总的来建堆的时间复杂度是O(N*logN)
🚝2.5堆的插入
像我们一般堆是用数组存储的,我们一般插入也是从数组后面插入,所以也就是在最后一个位置插入,而这个时候上面的堆都是有顺序的,我们可以用我们的向上调整算法来解决堆的插入。
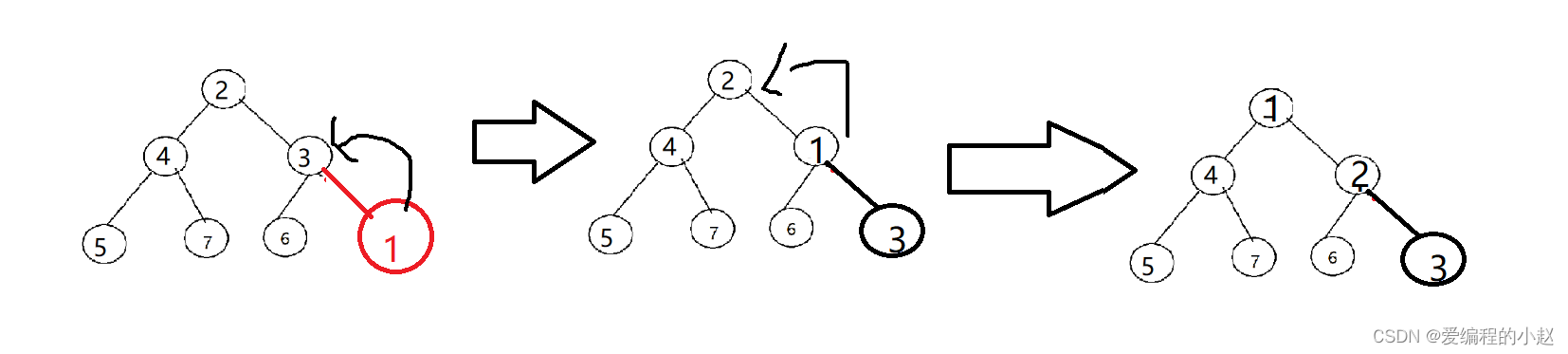
🚝2.6堆的删除
堆的删除,我们一般针对的是头元素的删除,这个时候我们采取的策略是将头元素和尾元素交换,然后让头元素,向下调整(因为下面的堆都已经是有顺序的)
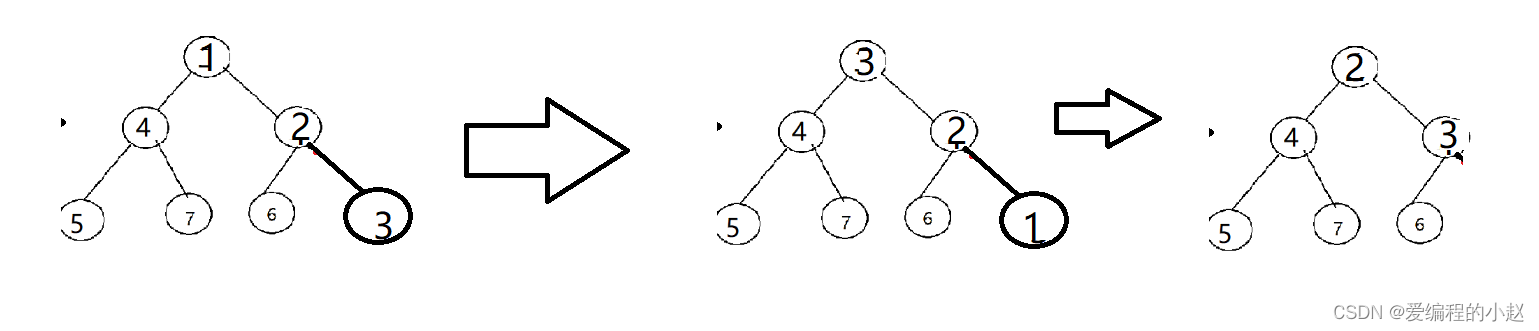
这样就可以完成头删了
🚝2.7建堆的代码实现
代码的实现我们的表示表示方式和前面的双亲节点是对应的(parent),然后子节点就是(child)
✈️2.7.1向下调整实现堆的建立
//小堆的建立
void Swap(int* a, int* b)//交换
{int tmp = *a;*a = *b;*b = tmp;
}
//小堆
void ADjustDown(int *a,int parent,int n)
{int child = parent * 2 + 1;//子节点和双亲节点的关系while (child < n){if (child + 1 < n && a[child + 1] < a[child])//选出两个孩子中较小的一个{child++;}if (a[child] < a[parent])//若子节点比双亲节点小{Swap(&a[child], &a[parent]);//交换接着向下进行parent = child;child = parent * 2 + 1;}else{break;}}
}
void Heap(int *a,int n)
{int i = (n - 1 - 1) / 2;//找到最后一个双亲节点while (i >= 0){ADjustDown(a, i, n);i--;}
}
int main()
{int a[10] = { 3,5,9,8,6,1,5,2,6,323 };Heap(a, 10);
}这里的主要方式就是我们前面的图所演示的,就是从最后一个双亲节点向下调整,然后调整过程中要小心不要让字节出了数组的范围,同时要记住子节点和双亲节点的关系。 这样可以方便我们的代码的实现。
✈️2.7.2向上调整实现堆的建立
//建立小堆
void Swap(int* a, int* b)//交换
{int tmp = *a;*a = *b;*b = tmp;
}
void ADjustUp(int*a,int child,int n)
{int parent = (child - 1) / 2;//双亲节点和子节点关系while (parent >= 0){if (a[child] < a[parent])//如果子节点比双亲节点小,那么交换,并且向上移动{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1 - 1) / 2;}else{break;}}
}
void Heap(int* a, int n)
{int i = 0;while (i < n)//从最上面开始建堆{ADjustUp(a, i, n);i++;}
}
int main()
{int a[10] = { 3,5,9,87,6,12,7,11,13,1 };Heap(a, 10);
}这里也基本上就是我们上面逻辑的实现,向上建堆,就要保证上面都是已经建好的堆,那么就得从首元素开始依次向下,建堆。
🚈 3.完整的堆的代码的实现
要想实现完整的堆的实现就要实现以下几个函数
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);这样我们的堆就可以像之前的链表顺序表等一样使用了。
🚝3.1堆的创建
和上面的代码逻辑基本一样。
这里我们主要采用的是向下排序建堆,因为向下排序的时间复杂度低。
void HeapCreate(Heap* hp, HPDataType* a, int n)
{hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (hp->_a == NULL){perror("malloc failed");}memcpy(hp->_a, a, n);hp->_capacity = n;hp->_size = n;int i = (n - 1 - 1) / 2;while (i >= 0){ADjustDown(a, i, n);i--;}
}🚝3.2堆的销毁
void HeapDestory(Heap* hp)
{free(hp->_a);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}🚝3.3堆的插入
void HeapPush(Heap* hp, HPDataType x)
{if (hp->_size == hp->_capacity){int newcapacity = (hp->_size == 0 ? 4 : hp->_capacity * 2);//如果没有内存就给4,有就是原来内存的双倍HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc failed");exit(-1);//退出程序,返回-1;}hp->_a = tmp;hp->_capacity = newcapacity;}hp->_a[hp->_size] = x;hp->_size++;ADjustUp(hp->_a, hp->_size - 1, hp->_size);//上面都是建好的堆,只需要向上调整即可
}🚝3.4堆的删除(头删)
void HeapPop(Heap* hp)
{if (!HeapEmpty(hp)){Swap(&(hp->_a[0]), &(hp->_a[hp->_size - 1]));//首尾交换ADjustDown(hp->_a, 0, hp->_size);//向下调整hp->_size--;//删除尾}else{return;}
}🚝3.5取堆顶元素的数据
HPDataType HeapTop(Heap* hp)
{if (!HeapEmpty(hp))//不是空集,返回首元素(即堆顶元素){return hp->_a[0];}else{return NULL;}
}🚝3.6 堆的数据个数
int HeapSize(Heap* hp)
{return hp->_size;
}🚝3.7堆的判空
int HeapEmpty(Heap* hp)
{return hp->_size == 0;//如果等式成立返回非零数,不成立返回零
}🚈 4.堆的应用堆排序
下面我们进入堆排序的学习,堆排序是我们的排序中比较优的一个排序,他具体是如何实现的呢?其实我们在前面的知识中已经发现了,就是如果我们建的是小堆,那小堆的堆顶元素一定是整个堆里面最小的,大堆的堆顶元素一定是最大的,那么如果我们想排一个顺序的方法就出来了,先把数组弄成一个大堆,再把第一个元素和最后一个元素交换,然后这个时候我们就排好了最大的一个,接着我们不管最后一个元素,对前面的n-1个元素再次建成大堆(其实只要进行向下调整就可以了因为下面的已经是大堆了),再重复上述操作。
那么我们就可以试着用代码实现了。
//建大堆
void ADjustDown(int* a, int parent, int n)
{int child = parent * 2 + 1;//子节点和双亲节点的关系while (child < n){if (child + 1 < n && a[child + 1] > a[child])//选出两个孩子中较大的一个{child++;}if (a[child] > a[parent])//若子节点比双亲节点大{Swap(&a[child], &a[parent]);//交换接着向下进行parent = child;child = parent * 2 + 1;}else{break;}}
}
void Heapsort(int* a, int n)
{int i = (n - 1 - 1) / 2;while (i >= 0){ADjustDown(a, i, n);i--;}//建堆while (n > 0){n--;Swap(&a[0], &a[n]);//交换首尾元素位置ADjustDown(a, 0, n);//下面都是建好的,只要向下调整就可以}
}
int main()
{int a[10] = { 3,5,9,87,6,12,7,11,13,1 };Heapsort(a,10);
}
✍5.结束语
好了小赵今天的分享就到这里了,如果大家有什么不明白的地方可以在小赵的下方留言哦,同时如果小赵的博客中有什么地方不对也希望得到大家的指点,谢谢各位家人们的支持。你们的支持是小赵创作的动力,加油。

如果觉得文章对你有帮助的话,还请点赞,关注,收藏支持小赵,如有不足还请指点,方便小赵及时改正,感谢大家支持!!!

相关文章:

数据结构(C):从初识堆到堆排序的实现
目录 🌞0.前言 🚈 1.堆的概念 🚈 2.堆的实现 🚝2.1堆向下调整算法 🚝2.2堆的创建(堆向下调整算法) ✈️2.2.1 向下调整建堆时间复杂度 🚝2.3堆向上调整算法 🚝2.…...
ChatGLM3-6B部署
ZhipuAI/chatglm3-6b 模型文件地址 chatglm3-6B-32k-int4 量化的模型地址 ChatGLM3 代码仓库 ChatGLM3 技术文档 cpolar http xxx 端口 /anaconda3/envs/chatglm2/lib/python3.8/site-packages/gradio$ networking.py 硬件环境 最低要求: 为…...

代码随想录35期Day54-JavaScript
Day54题目 ### LeetCode739每日温度 核心思想:今天主要是学会单调栈的使用.找到比元素更大的下一个元素,如果比栈顶元素小就入栈,否则就出栈顶元素,当前元素就是比栈顶元素大的"下一个更大的元素". /*** param {number[]} temperatures* return {number[]}*/ var …...

把自己的服务器添加到presearch节点
Presearch is a scam. Before, judging by the price of the token you should have been able to get between $150-$200 after 12-13 months of regular searches. "If you use this service for the next 11 years you will have earned $30!" Presearch大约需要…...

Open3D(C++) OTSU点云二值化
目录 一、算法原理二、代码实现三、结果展示1、原始点云2、二值化本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 最大类间方差法(Between-class scatter method)是一种用于分割的方法,它通过计算图…...

浔川python社获得全网博主原力月度排名泸州地区第二名!
今日,浔川python社在查看全网博主原力月度排名泸州地区时,一看就震惊啦! 全网博主原力月度排名泸州地区排名榜单 全网博主原力月度排名泸州地区第二名为:浔川python社。 感谢粉丝们的支持!浔川python社还会继续努力&a…...
)
第二站:Java——集合框架的深邃海洋(续)
### Java——集合框架的深邃海洋(续) 在我们的Java集合框架探索之旅中,我们已经涉足了基本操作、高级特性,现在让我们深入探讨一些特定场景下的应用和进阶技巧,比如集合的分区操作、分组、并行流的性能考量࿰…...

linux系统下,mysql增加用户
首先,在linux进入mysql mysql -u root -p 然后查看当前用户: select user,host from user; 增加用户语句: CREATE USER 用户名host范围 IDENTIFIED BY 密码;...
)
Java数据结构与算法(最长回文子串中心扩散法)
前言 回文子串是练习数据结构和算法比较好的使用场景,可以同时练习到双指针、动态规划等一些列算法。 实现原理 中心扩散算法实现。这里定义最长回文子串长度的大小为maxLen,起点位置为0. 奇数个数为中心点和偶数个数为中心点分别计算回文长度大小。…...

基于Python网络招聘数据可视化分析系统的设计与实现
基于Python网络招聘数据可视化分析系统的设计与实现 Design and Implementation of Python-based Network Recruitment Data Visualization Analysis System 完整下载链接:基于Python网络招聘数据可视化分析系统的设计与实现 文章目录 基于Python网络招聘数据可视化分析系统的…...

【Linux】Linux工具——gcc/g++
1.使用vim更改信用名单——sudo 我们这里来补充sudo的相关知识——添加信任白名单用户 使用sudo就必须将使用sudo的那个账号添加到信用名单里,而且啊,只有超级管理员才可以添加 信用名单在/etc/sudoers里 我们发现它的权限只是可读啊,所以…...
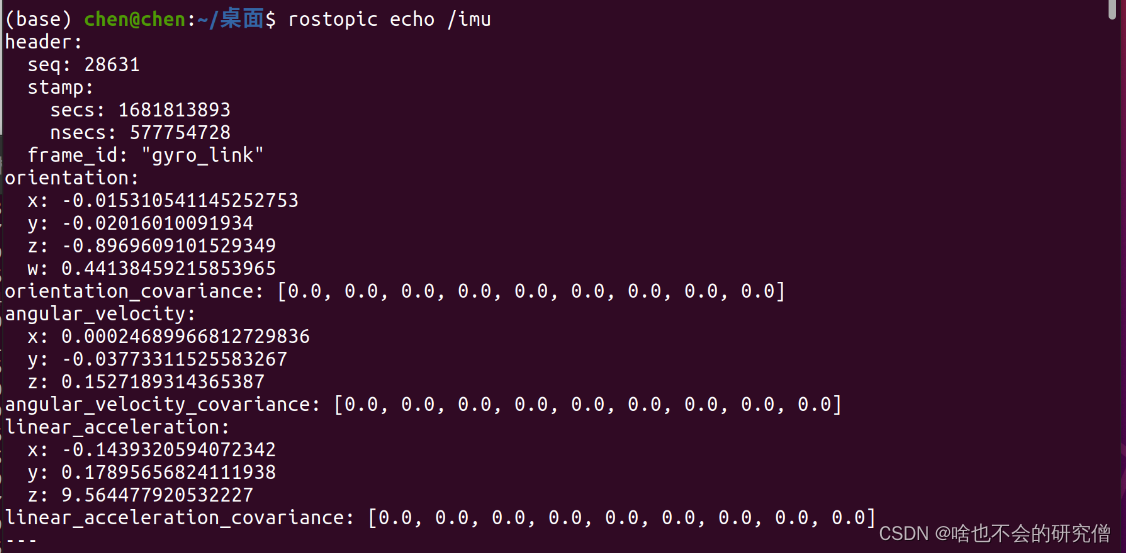
【惯性传感器imu】—— WHEELTEC的惯导模块的imu的驱动安装配置和运行
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、IMU驱动安装1. 安装依赖2. 源码的下载3. 编译源码(1) 配置固定串口设备(2) 修改luanch文件(3) 编译 二、启动IMU1. 运行imu2. 查看imu数据 总结 前言 WHEE…...

Linux提权一
#信息收集 当前主机的操作系统 hostnamectl cat /etc/*-release lsb_release -a cat /etc/lsb-release # Debain cat /etc/redhat-release # Redhat cat /etc/centos-release # Centos cat /etc/os-release # Ubuntu cat /etc/issue 当前主机的内核版本 hostnamectl uname -a …...

Vue.js中如何实现以列表首列为表头
前言 一般情况table列表的展示,列头都在第一横行,此方法用于列头在第一列的情况。 效果图 核心代码 <template><div><table class"data-table"><tr v-for"(column, columnIndex) in columns" :key"col…...

如果孙宇晨和贾跃亭能够握手,或许将会上演新的戏码
就在贾跃亭宣布将进行个人IP的商业化不久,便迎来了回应,并且这一次给予贾跃亭回应的,同样是一个颇具争议性的人物——孙宇晨。 根据孙宇晨最新发布的视频显示,他愿意投资贾跃亭「做一个新的个人IP化的公司」,并且将会…...
渲染100为什么是高性价比网渲平台?渲染100邀请码1a12
市面上主流的网渲平台有很多,如渲染100、瑞云、炫云、渲云等,这些平台各有特色和优势,也都声称自己性价比高,以渲染100为例,我们来介绍下它的优势有哪些。 1、渲染100对新用户很友好,注册填邀请码1a12有3…...
Jenkins流水线pipeline--基于上一章的工作流程
1流水线部署 1.流水线文本名Jenkinsfile,将流水线放入gitlab远程仓库代码里面 2pipeline脚本 Jenkinsfile文件内容 pipeline {agent anyenvironment {key"value"}stages {stage("拉取git仓库代码") {steps {deleteDir()checkout scmGit(branches: [[nam…...

比较Rust和Haskel
在比较Rust和Haskell时,我们可以从多个维度来分析它们各自的优势。以下是Rust相对于Haskell的优势,以及Haskell相对于Rust的优势: Rust比Haskell强的方面: 内存安全与并发性: Rust通过独特的所有权系统和借用检查器在…...

RedisTemplate的Long类型使用increment自增报错
问题描述 代码如下 Resourceprivate RedisTemplate<String,String > redisTemplate;redisTemplate.opsForValue().set("testKey", 0L); redisTemplate.opsForValue().increment("testKey");工作里用Long类型存储评论数,在使用increment自…...

【代码随想录训练营】【Day 36】【贪心-3】| Leetcode 1005, 134, 135
【代码随想录训练营】【Day 36】【贪心-3】| Leetcode 1005, 134, 135 需强化知识点 题目 1005. K 次取反后最大化的数组和 贪心:翻转绝对值最小的数思路:将数组按绝对值降序排序后,从左向右遍历数组,如果遇到小于0的数并且还…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
