数学建模 —— 层次分析法(2)
目录
一、层次分析法(AHP)
二、构造比较判断矩阵
2.1 两两比较法
三、单准则下的排序及一致检验
3.1 单准则下的排序
3.2 一致性检验
四、层次总排序
4.1 层次总排序的步骤
4.2 总排序一致性检验
一、层次分析法(AHP)
方法:层次分析法(Analytic Hierarchy Process)简称AHP (美国运筹学家T.L.Saaty教授在70年代中期提出)是指将决策问题的有关元素分解成目标、准则、方案等层次,在此基础上进行定性分析和定量分析的一种决策方法.
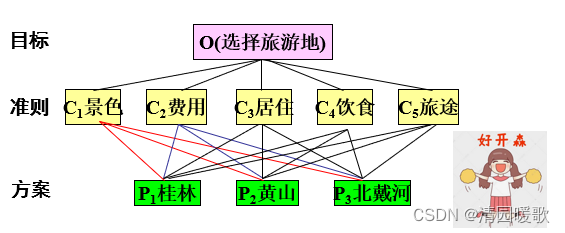
运用层次分析法建模,大体上分成四个步骤:
⑴建立递阶层次结构;
⑵构造比较判别矩阵;
⑶在单准则下的排序及一致性检验;
⑷总的排序选优。
二、构造比较判断矩阵
2.1 两两比较法
当以上一层次某个因素C作为比较准则时,可用一个比较标度aij来表达下一层次中第i个因素与第j个因素的相对重要性(或偏好优劣)的认识。aij的取值一般取正整数1—9(称为标度)及其倒数。由aij构成的矩阵称为比较判断矩阵A=(aij)。关于aij取值的规则见下表
| 元素 | 标度 | 规 则 |
| aij | 1 | 以上一层某个因素为准则,本层次因素i与因素j相比, 具有同样重要。 |
| 3 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j稍微重要。 | |
| 5 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j明显重要。 | |
| 7 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j强烈重要。 | |
| 9 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j极端重要。 |
aij取值也可以取上述各数的中值2,4,6,8及其倒数,即若因素i与因素j比较得aij,则因素j与因素i比较得1/aij。
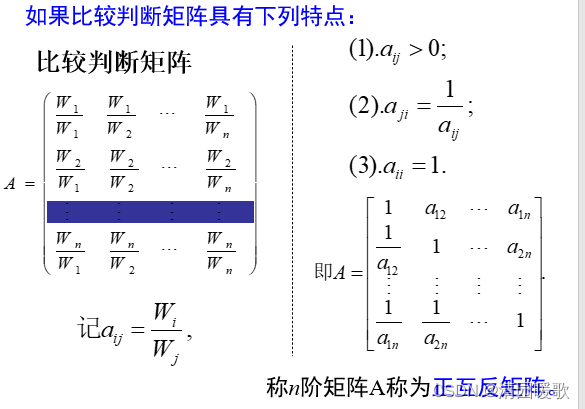
设n阶矩阵A=(aij)为正互反矩阵, 若对于一切i,j,k,都有aijajk=aik, i,j,k=1,2,…,n,称A为一致矩阵.
三、单准则下的排序及一致检验
3.1 单准则下的排序
根据比较判断矩阵如何求出各因素u1,u2,…,un , 对于准则的相对排序权重的过程称为单准则下的排序。
(1)理论依据
定理3.1.1 (Perron定理):
设n阶方阵A>O, lmax为A的模最大特征根,则
⑴ lmax必为正特征根,且对应特征向量为正向量;
⑵对于A的任何其它特征值,恒有|l|<lmax ;
⑶ lmax为A的单特征根,因而它所对应的特征向量除相差一个常数因子外是唯一的。
定理3.1.2 对于任何一个正互反矩阵均有lmax ³ n, 其中lmax为A的模最大特征根。
定理3.1.3 n阶正互反矩阵A=(aij)为一致矩阵的充分必要条件是A的最大特征根为n.
(2)求正互反矩阵排序向量的方法
①特征根方法(EVM)
对于正矩阵,有一种求特征向量的简易算法(幂法)。下面的定理为幂法提供了理论依据。

②和法

③根法

3.2 一致性检验


引入随机一致性指标RI

所以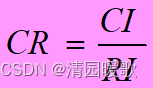
一般当CR<0.1时,认为A的不一致程度在容许范围之内,有满意的一致性,通过一致性检验。可用其归一化特征向量作为权向量,否则要重新构造成对比较矩阵A,对 aij 加以调整。
四、层次总排序
计算同一层次中所有元素对于最高层(总目标)的相对重要性标度(又称排序权重向量)称为层次总排序。
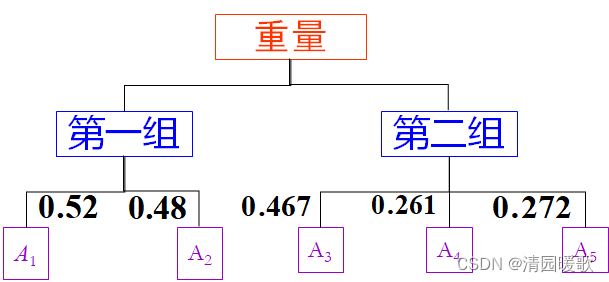
4.1 层次总排序的步骤

4.2 总排序一致性检验
人们在对各层元素作比较时,尽管每一层中所用的比较尺度基本一致,但各层之间仍可能有所差异,而这种差异将随着层次总排序的逐渐计算而累加起来,因此需要从模型的总体上来检验这种差异尺度的累积是否显著,检验的过程称为层次总排序的一致性检验。


相关文章:

数学建模 —— 层次分析法(2)
目录 一、层次分析法(AHP) 二、构造比较判断矩阵 2.1 两两比较法 三、单准则下的排序及一致检验 3.1 单准则下的排序 3.2 一致性检验 四、层次总排序 4.1 层次总排序的步骤 4.2 总排序一致性检验 一、层次分析法(AHP) 方…...

Nvidia Jetson/Orin +FPGA+AI大算力边缘计算盒子:人工智能消防应用
青鸟消防股份有限公司成立于2001年6月,于2019年8月在深圳证券交易所挂牌上市,成为中国消防报警行业首家登陆A股的企业。公司始终聚焦于消防安全与物联网领域,主营业务为“一站式”消防安全系统产品的研发、生产和销售。公司产品已覆盖了火灾报…...

Flutter 中的 KeepAlive 小部件:全面指南
Flutter 中的 KeepAlive 小部件:全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架,它允许开发者使用 Dart 语言构建高性能、美观的移动、Web 和桌面应用。在 Flutter 的丰富组件库中,KeepAlive 是一个用于维护组件活跃状态的组件&…...

C语言 恼人的结合性和优先级和副作用
结合性和优先级和副作用 1.优先级2.结合性3.副作用4.简单区分i,i,i1;ii1;ii 1.优先级 优先级指的是,如果⼀个表达式包含多个运算符,哪个运算符应该优先执⾏。各种运算符的优先级是 不⼀样的。 在C语言中&a…...

Vue——初识组件
文章目录 前言页面的构成何为组件编写组件组件嵌套注册 效果展示 前言 在官方文档中,对组件的知识点做了一个很全面的说明。本篇博客主要写一个自己的案例讲解。 vue 官方文档 组件基础 页面的构成 说到组件之前,先大致说明下vue中页面的构成要素。 在…...

MQ消息丢失/重复/顺序/挤压
rabbitmq消息丢失解决 rocketMq解决消息丢失 RocketMQ事务消息概要 RocketMQ事务消息是指应用本地事务和发送消息操作可以被定义到全局事务中,要么同时成功,要么同时失败。 采用了2PC(两阶段提交) 补偿机制(事务状态回…...

利用Quarkus构建高效微服务——Java的云原生革新
引言: 在微服务架构和容器技术日益成为企业开发标准的今天,Java开发者面临着如何将传统Java应用转型为高效、轻量级且易于扩展的云原生应用的挑战。Quarkus框架的出现,正是为了解决这一问题,它不仅能够提升Java在Kubernetes环境中…...

python 批量ts合并成一个mp4
首先,确保你已经安装了ffmpeg。 然后再次保证所有ts文件放在同一个文件夹中,并且依次命名为 1.ts 、 2.ts 、 3.ts 、 4.ts 、 4.ts 。。。 Python完整代码如下:(ffmpeg_batch_merge_ts.py文件) #!/usr/bin/python3 # -*- coding: UTF-8 -*…...
Java | Leetcode Java题解之第129题求根节点到叶节点数字之和
题目: 题解: class Solution {public int sumNumbers(TreeNode root) {if (root null) {return 0;}int sum 0;Queue<TreeNode> nodeQueue new LinkedList<TreeNode>();Queue<Integer> numQueue new LinkedList<Integer>();…...

SpringBoot【注解 01】@Scheduled实现定时任务的串行和并行执行
在SpringBoot中,如果使用Scheduled注解来定义多个定时任务,默认情况下这些任务将会被安排在一个单线程的调度器中执行。这意味着,这些任务将会串行执行,而不是并行执行。当一个任务正在执行时,其他被触发的任务将会等待…...

【工具】redis的安装使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Redis简介二、Redis的安装使用三、本文总结 前言 提示:这里可以添加本文要记录的大概内容: 随着开发语言及人工智能工具的普及&am…...

汇编:数据定义数据填充
数组的定义 在32位汇编语言中,定义数组时,通常使用定义数据指令(如 DB, DW, DD,DQ )和标签来指定数组的名称和内容。DB定义字节数组(每个元素占1字节)、DW定义字数组(每个元素占2字节ÿ…...
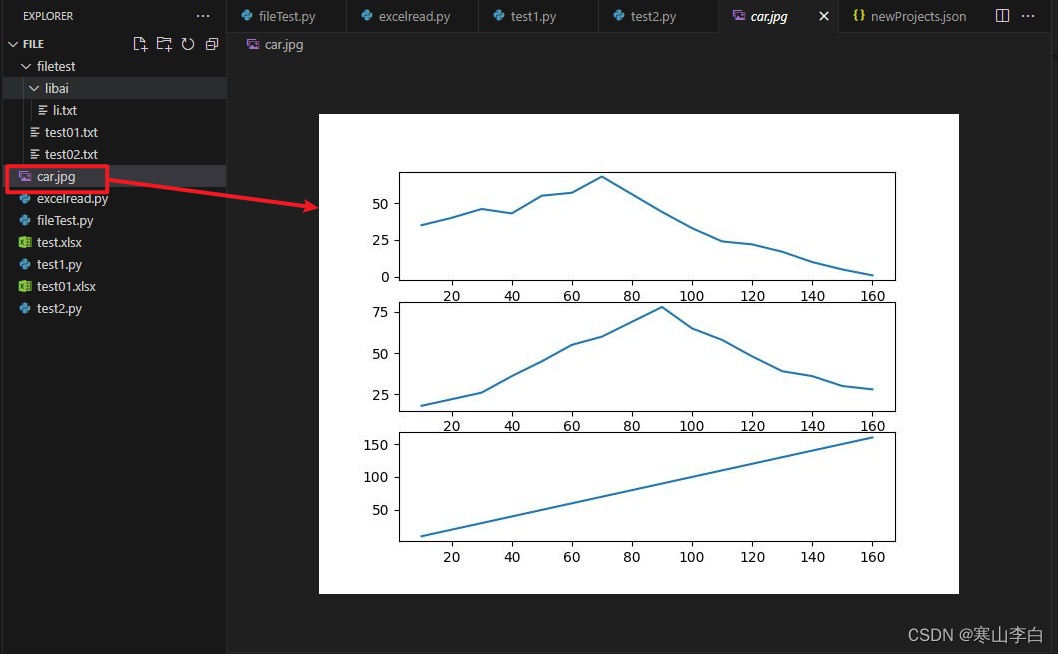
Python画图(多图展示在一个平面)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

python-web应用程序-Django数据库-操作表中的数据
python-web应用程序-Django数据库-操作表中的数据 一、新增数据 类.objects.create(字段名 字段值,字段名 字段值,...)导入models包 models.User.objects.create(nameyulin,sex0,info三好学生)即可对数据进行操作 二、删除数据 类.objects.filter(…...
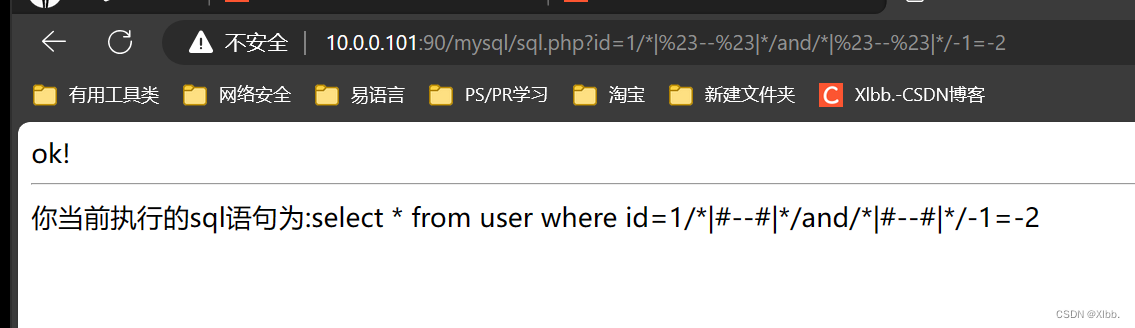
绕过WAF(Web应用程序防火墙)--介绍、主要功能、部署模式、分类及注入绕过方式等
网站WAF是一款集网站内容安全防护、网站资源保护及网站流量保护功能为一体的服务器工具。功能涵盖了网马/木马扫描、防SQL注入、防盗链、防CC攻击、网站流量实时监控、网站CPU监控、下载线程保护、IP黑白名单管理、网页防篡改功能等模块。能够为用户提供实时的网站安全防护&…...
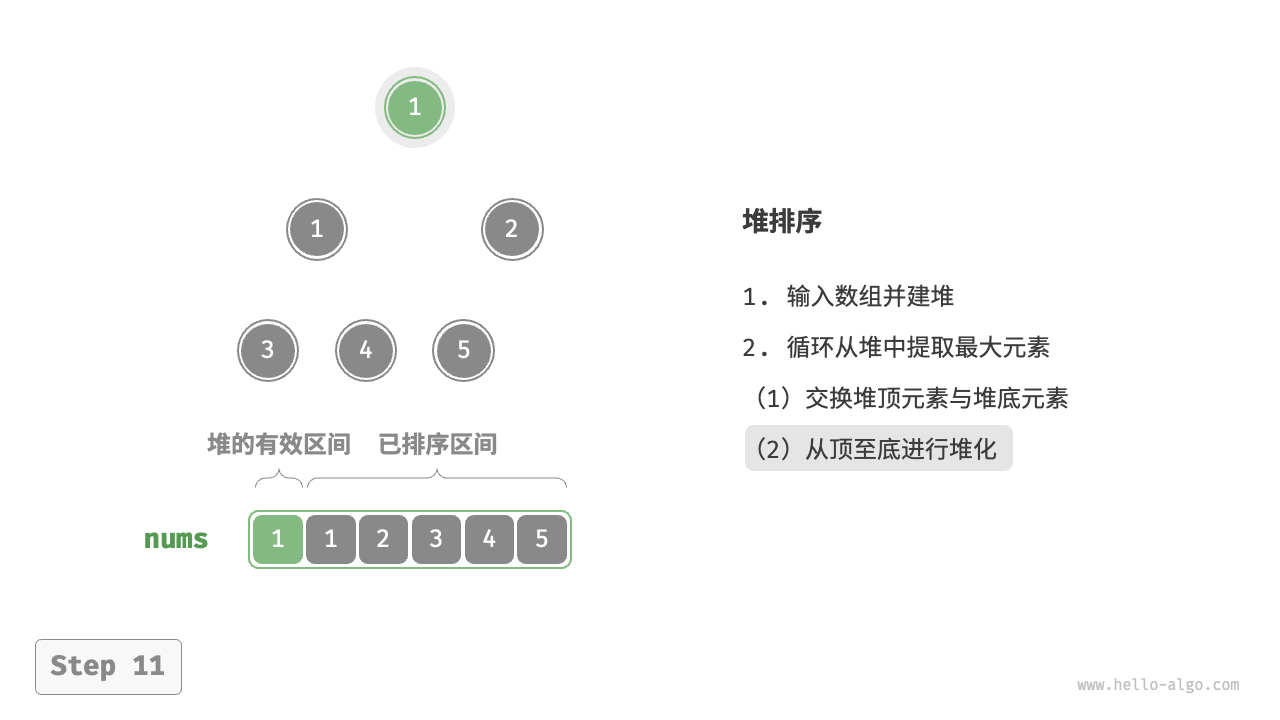
11.7 堆排序
目录 11.7 堆排序 11.7.1 算法流程 11.7.2 算法特性 11.7 堆排序 Tip 阅读本节前,请确保已学完“堆“章节。 堆排序(heap sort)是一种基于堆数据结构实现的高效排序算法。我们可以利用已经学过的“建堆操作”和“元素出堆操作”…...

Patchwork++:基于点云的快速、稳健的地面分割方法
1. 背景 论文发表在2022IROS,是Patchwork的改进版本。算法通过数学方法进行快速而鲁棒性很强的地面分割,在智能机器人上的可操作性非常强。通过微调算法,可以应用于16-beams等多种规格的激光雷达。由于激光雷达点云数据标注的难度非常大&…...

Llama改进之——分组查询注意力
引言 今天介绍LLAMA2模型引入的关于注意力的改进——分组查询注意力(Grouped-query attention,GQA)1。 Transformer中的多头注意力在解码阶段来说是一个性能瓶颈。多查询注意力2通过共享单个key和value头,同时不减少query头来提升性能。多查询注意力可能导致质量下…...
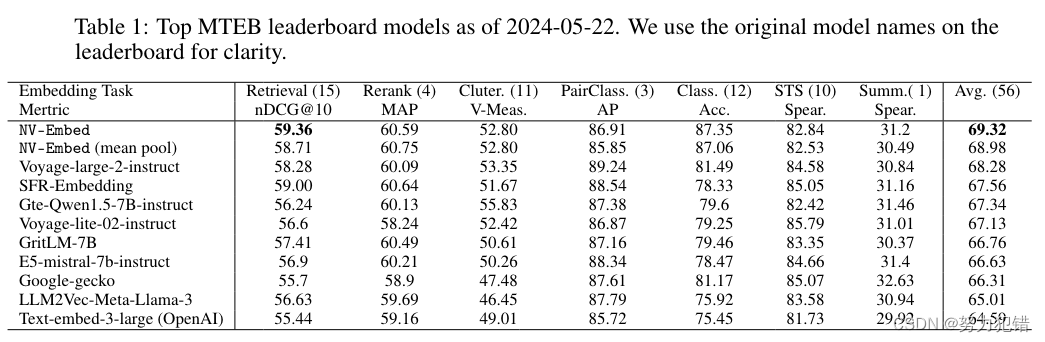
英伟达开源新利器NV-Embed向量模型,基于双向注意力的LLM嵌入模型,MTEB 56项任务排名第一
前言 文本嵌入模型能够将文本信息转化为稠密的向量表示,并在信息检索、语义相似度计算、文本分类等众多自然语言处理任务中发挥着关键作用。近年来,基于解码器的大型语言模型 (LLM) 开始在通用文本嵌入任务中超越传统的 BERT 或 T5 嵌入模型,…...

JVM之【GC-垃圾清除算法】
Java虚拟机(JVM)中的垃圾收集算法主要分为以下几种: 标记-清除算法(Mark-Sweep)复制算法(Copying)标记-整理算法(Mark-Compact)分代收集算法(Generational C…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
