基于学习的决策树
基于学习的决策树概述
决策树是一种监督学习方法,广泛应用于分类和回归任务中。基于学习的决策树模型通过学习数据中的特征来构建树状结构,帮助做出决策。以下是对基于学习的决策树的详细介绍,包括其基本概念、工作流程、构建算法、优势和挑战,以及主要应用领域。
基本概念
1. 决策树结构
决策树由节点和边组成。树的根节点代表整个数据集,内部节点表示数据集上的特征,边表示特征的取值,叶节点表示分类结果或回归值。每个内部节点对应一个决策规则,根据特征的不同取值,将数据集划分为子集。
2. 分类树与回归树
- 分类树(Classification Tree):用于分类任务,叶节点表示类别标签。
- 回归树(Regression Tree):用于回归任务,叶节点表示连续值。
工作流程
- 数据准备:收集和预处理数据,包括处理缺失值、归一化特征等。
- 特征选择:选择用于分割数据集的特征,根据某些标准(如信息增益、基尼指数)选择最优特征。
- 节点分裂:根据选择的特征分裂数据集,递归地创建子节点,直到满足停止条件(如树的最大深度、叶节点的最小样本数)。
- 树剪枝:对过拟合的树进行剪枝,移除不必要的节点,以提高泛化能力。
- 预测与评估:使用构建好的决策树进行预测,并评估模型性能。
构建算法
1. ID3(Iterative Dichotomiser 3)
- 信息增益:选择具有最高信息增益的特征进行分裂。信息增益衡量特征对分类的不确定性减少程度。
- 步骤:
- 计算所有特征的信息增益。
- 选择信息增益最大的特征进行分裂。
- 对分裂后的子集递归执行上述步骤。
2. C4.5
- 信息增益率:改进了ID3算法,使用信息增益率来选择特征,以避免偏向多值特征。
- 步骤:
- 计算所有特征的信息增益率。
- 选择信息增益率最大的特征进行分裂。
- 对分裂后的子集递归执行上述步骤。
3. CART(Classification and Regression Trees)
- 基尼指数或方差:用于分类树时,选择基尼指数最小的特征;用于回归树时,选择方差最小的特征。
- 步骤:
- 计算所有特征的基尼指数(分类)或方差(回归)。
- 选择基尼指数或方差最小的特征进行分裂。
- 对分裂后的子集递归执行上述步骤。
优势
- 易于理解和解释:决策树的结构直观,易于可视化,便于解释和分析。
- 非线性特征关系:能够捕捉数据中非线性特征之间的关系。
- 处理缺失值:可以处理数据集中缺失值,不需要进行大量预处理。
- 较少的数据预处理:不需要特征缩放或归一化。
挑战
- 过拟合:决策树容易对训练数据过拟合,影响泛化能力。剪枝技术和设置适当的停止条件可以缓解过拟合问题。
- 稳定性差:对数据中的噪声和小的扰动敏感,不稳定。
- 计算复杂度:在处理高维数据时,构建决策树的计算复杂度较高,可能导致效率低下。
- 偏差问题:单棵决策树可能表现出高方差或高偏差,需要通过集成方法(如随机森林)来改善。
主要应用领域
- 分类任务:如垃圾邮件检测、图像分类、疾病诊断等。
- 回归任务:如房价预测、股票价格预测、销量预测等。
- 特征选择:在构建复杂模型前,使用决策树进行特征选择。
- 数据探索和分析:帮助理解数据中的特征关系和模式。
总结
基于学习的决策树是一种强大且易于理解的监督学习方法,适用于分类和回归任务。通过特征选择、节点分裂和树剪枝等步骤,决策树能够从数据中学习到有效的决策规则。尽管存在过拟合、稳定性差和计算复杂度高等挑战,但通过剪枝技术、集成方法等手段,决策树在各种应用领域中展现出广泛的应用前景。
相关文章:

基于学习的决策树
基于学习的决策树概述 决策树是一种监督学习方法,广泛应用于分类和回归任务中。基于学习的决策树模型通过学习数据中的特征来构建树状结构,帮助做出决策。以下是对基于学习的决策树的详细介绍,包括其基本概念、工作流程、构建算法、优势和挑…...

godot.bk2
1.$node_name 其实 就是 get_node 的语法糖 2.场景内部用get_node,场景外部用信号 这是自定义信号的绑定,如果是内置信号,直接右键点击链接到一个函数即可 3.场景切换和摄像头一直居中 4.class_name命名一个类,extends继承&…...

STM32 IIC 使用 HAL 库操作eeprom
在STM32上通过I2C接口(注意:在标准STM32库中,I2C接口通常被写为"I2C"而不是"IIC")与EEPROM芯片通信时,你需要遵循I2C通信协议,并使用STM32的HAL库或标准外设库(如果适用&am…...
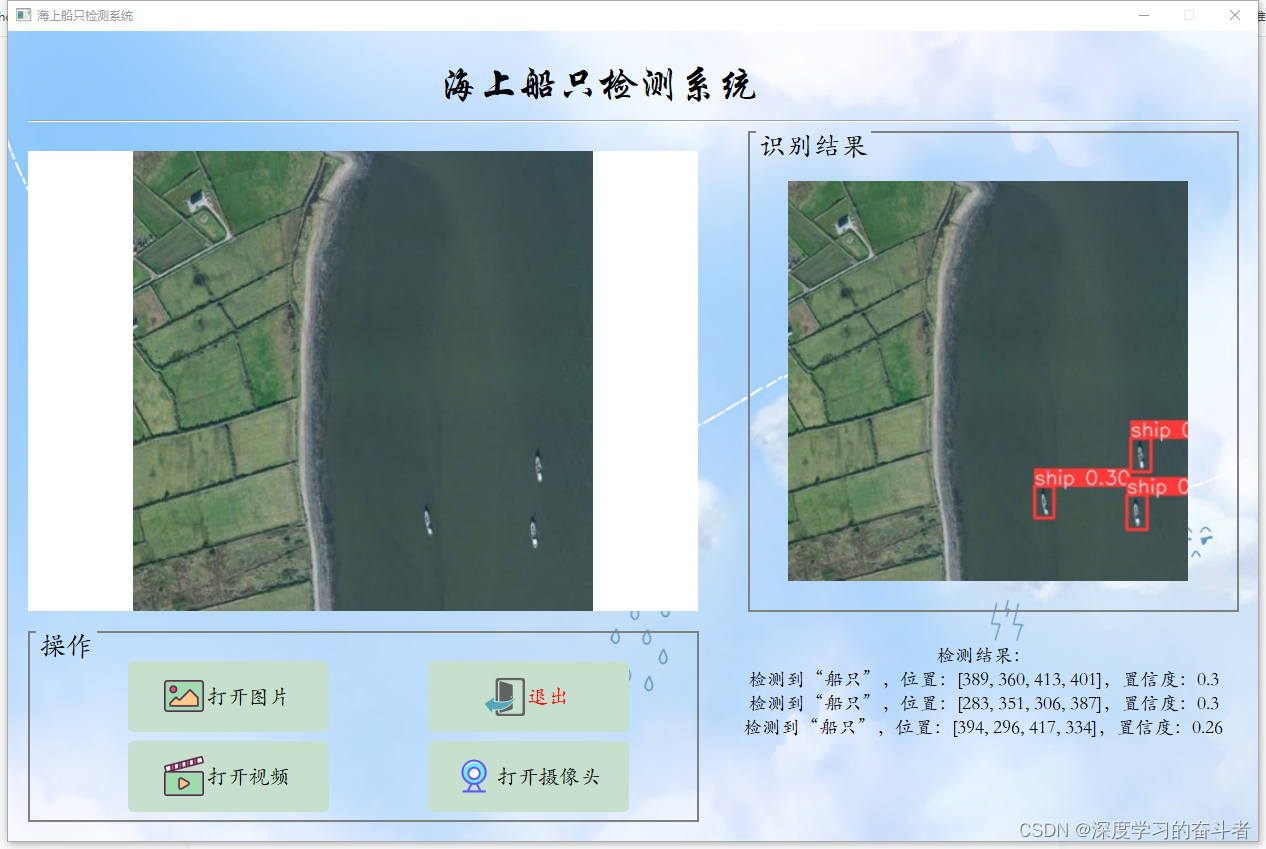
YOLOv8+PyQt5海洋船只检测(可以重新训练,yolov8模型,从图像、视频和摄像头三种路径识别检测)
1.效果视频:海洋船只检测yoloV8检测(https://mbd.pub/o/bread/mbd-ZpaYk55r)_哔哩哔哩_bilibili资源包含可视化的海洋船只检测系统,可对于高空拍摄到的海洋图片进行轮船检测,基于最新的YOLOv8训练的海洋船只检测模型&a…...

PCL 高阶多项式曲线回归拟合(二维)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 高阶多项式曲线回归(Polynomial Regression)是一种线性回归模型的扩展,它允许数据拟合一个非线性的曲线。虽然多项式本身是非线性的,但我们可以通过引入新的变量(例如,原始变量的平方、立方等)来将问题转化为…...

深入理解 Python3 函数:从基础语法到高级应用
Python3 函数是构建模块化代码的基本单位,允许我们将代码组织成独立的、可重用的块。本文将详细介绍 Python3 函数的基本语法、常用命令、示例、应用场景、注意事项,并进行总结。 基本语法 在 Python 中,函数的定义使用 def 关键字…...
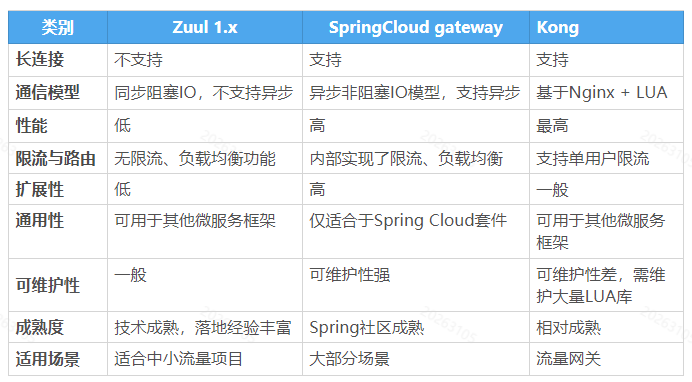
03_初识Spring Cloud Gateway
文章目录 一、网关简介1.1 网关提出的背景1.2 网关在微服务中的位置1.3 网关的技术选型1.4 补充 二、Spring Cloud Gateway的简介2.1 核心概念:路由(Route)2.2 核心概念:断言(Predicate)2.3 核心概念&#…...
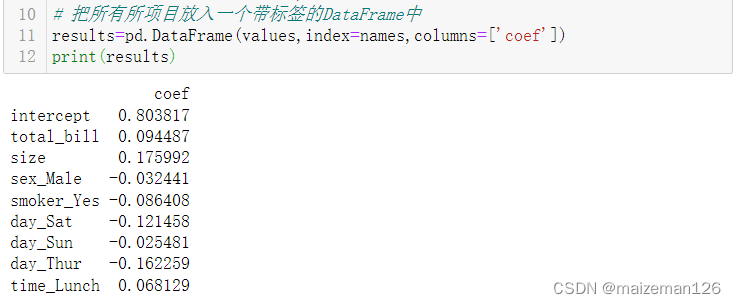
python数据分析——线性模型
参考资料:活用pandas库 1、简单线性回归 线性回归的目标是描述响应变量(或“因变量”)和预测变量(也称“特征”、“协变量”、“自变量”)之间的直线关系。本例中将讨论tips数据集中的total_bill对tip的影响。 # 导入…...

网络原理——HTTP/HTTPS ---- HTTPS
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 目录 HTTPS加密与解密HTTPS的工作流程使用对称密钥来加密使用非对称密钥 来对 对称密钥进行加密第三方公证总结 HTTPS https本质上就是在http的基础之上 增加了加密层,抛开加密层之后,剩下的部…...
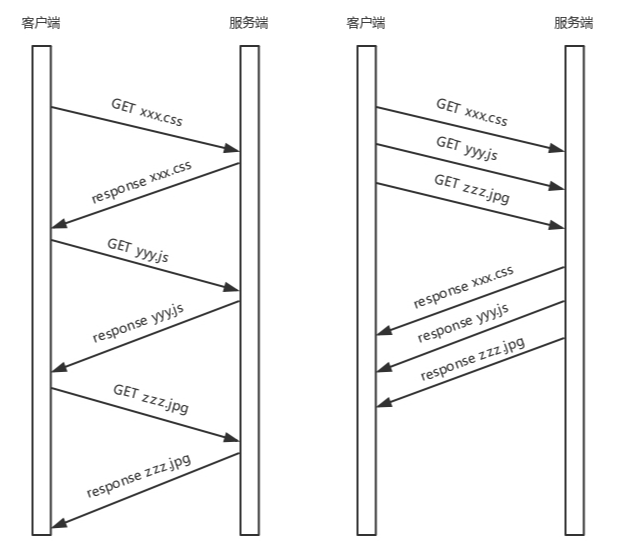
网络协议二
一、套接字Socket 基于 TCP UDP 协议的 Socket 编程,在讲 TCP 和 UDP 协议的时候,我们分客户端和服务端,在写程序的时候,我们也同样这样分。 在网络层,Socket 函数需要指定到底是 IPv4 还是 IPv6,分别对应设…...

内存映射mmap技术详解
一、mmap基础概念 mmap 即 memory map,也就是内存映射。mmap 是一种内存映射文件的方法,即将一个文件或者其它对象映射到进程的地址空间,实现文件磁盘地址和进程虚拟地址空间中一段虚拟地址的一一对映关系。实现这样的映射关系后,…...

react 合成事件
React合成事件-CSDN博客 当然,很高兴为你解释React中的合成事件概念,非常适合React初学者理解。 想象一下,你正在组织一场派对,为了让派对顺利进行,你需要管理各种活动,比如游戏、音乐和食物分配。但是&a…...
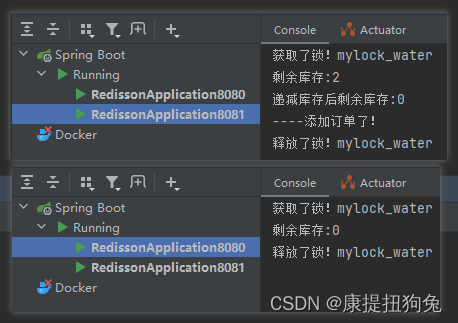
springboot配置集成RedisTemplate和Redisson,使用分布式锁案例
文章要点 自定义配置属性类集成配置RedisTemplate集成配置分布式锁Redisson使用分布式锁简单实现超卖方案 1. 项目结构 2. 集成RedisTemplate和Redisson 添加依赖 依赖的版本与继承的spring-boot-starter-parent工程相对应,可写可不写 <!--spring data redis…...

随机数相关
产生随机数对象 固定写法: Random 随机数变量名 new Random();Random r new Random();生成随机数 int i r.Next(); //生成一个非负数的随机数 Console.WriteLine(i);i r.Next(100); // 生成一个 0~99的随机数 左边始终是0 左包含 右边是100 右不包含 Consol…...
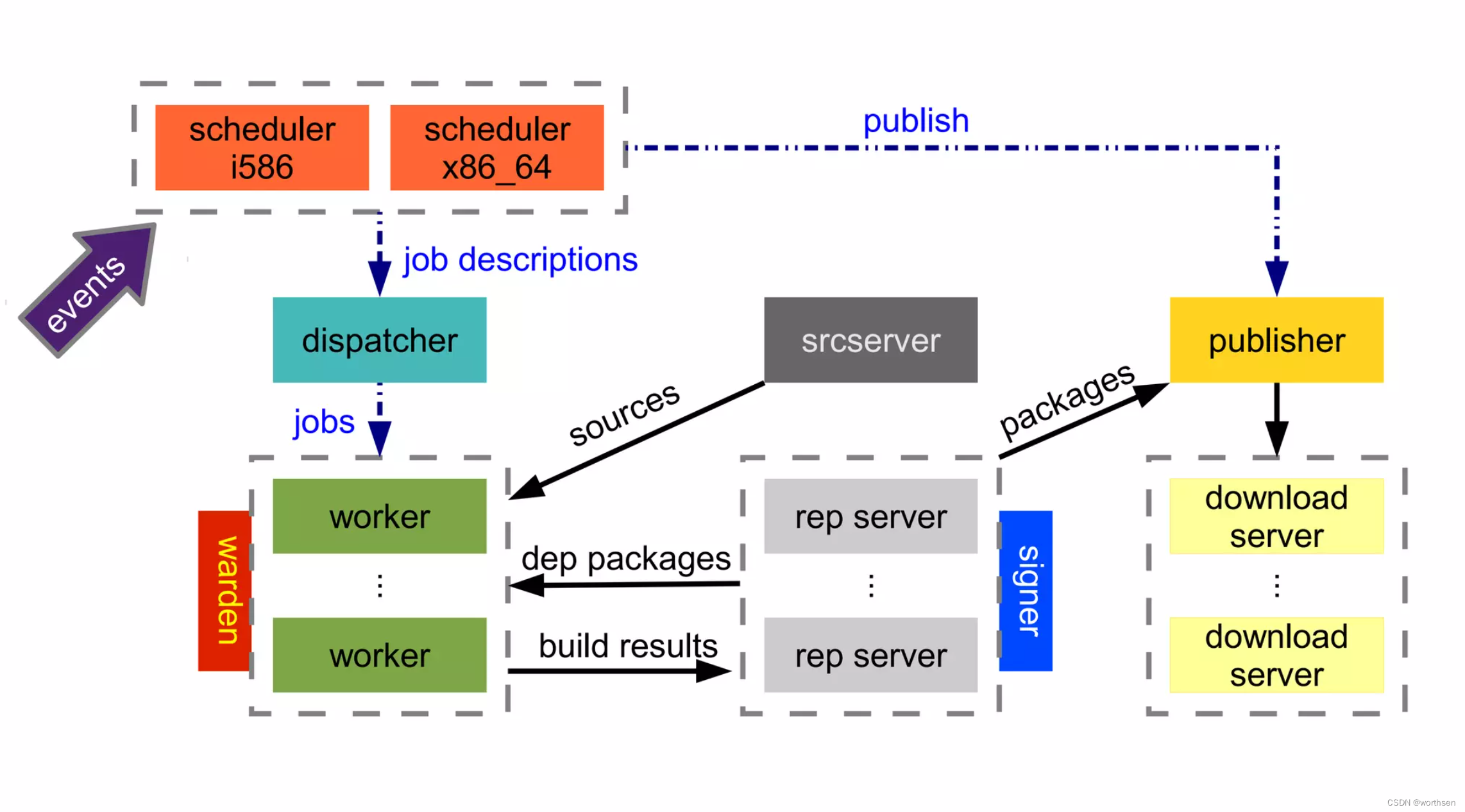
EulerMaker Yocto Open Build Service
EulerMaker & Yocto & Open Build Service 1 介绍1.1 概述 2 工具2.1 Yocto 【嵌入式领域】介绍目标好处三大关键组件创建流程发行版本 2.2 Open Build Service 【OBS】【服务器领域】介绍应用 2.3 EulerMaker 【全场景】介绍特性需求背景(1)能支…...
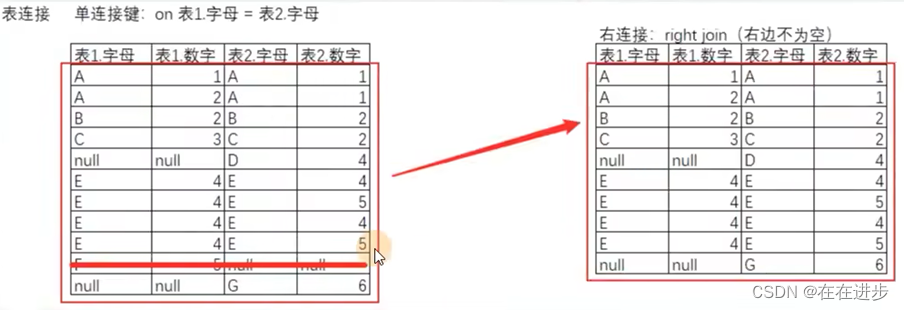
SQL面试问题集
目录 Q.左连接和右连接的区别 Q.union 和 union all的区别 1、取结果的交集 2、获取结果后的操作 Q.熟悉开窗函数吗?讲一下row_number和dense_rank的区别。 Q.hive行转列怎么操作的 Q.要求手写的题主要考了聚合函数和窗口函数,row_number()&#…...

基于单片机的八路抢答器设计论文
绪 论1.1 课题研究的相关背景 抢答器是一种应用非常广泛的设备,在各种竞赛、抢答场合中,它能迅速、客观地分辨出最先获得发言权的选手。早期的抢答器只由几个三极管、可控硅、发光管等组成,能通过发光管的指示辩认出选手号码。现在大多数抢答器均使用单片机(如MCS-5…...

一个最简单基于spring的websocket服务端+客户端实现案例
1、服务端 代码分为两部分: 一个是服务器终端类:用java注解来监听连接ServerEndpoint、连接成功OnOpen、连接失败OnClose、收到消息等状态OnMessage import org.springframework.stereotype.Component;import javax.websocket.*; import javax.websoc…...

三.二、关于 Vue.js 中`transition`组件使用:页面切换动画和标签移动动画都是要用到的
一、引言 在 Vue.js 中,transition组件提供了一种简单而强大的方式来实现页面过渡效果。它可以让元素在状态改变时,如进入或离开视图时,以平滑的动画方式进行过渡。通过transition,我们可以为应用增添更加生动和吸引人的用户体验…...

指纹考勤系统
目录 1.课题研究目的和内容 1.1 课题研究目的 1.2 课题研究内容 2.系统总体方案设计及功能模块介绍 2.1总体方案设计 2.2 ATK-301模块介绍 2.3 TFTLCD显示功能模块介绍 2.4 蜂鸣器报警功能模块介绍 2.5 时钟模块介绍 3.系统硬件设计与实现 3.1 系统硬件电…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
