算法 | 刷题日记
1.递归通常是用栈来实现的
递归在其本质上是通过函数调用栈(Call Stack)来实现的,而不是队列(Queue)。当你调用一个函数时,该函数的局部变量、参数和返回地址会被压入(push)到一个由系统维护的调用栈中。当函数执行完毕后,这些数据会被从栈中弹出(pop),并且控制权会返回给调用者。
递归函数调用也遵循同样的模式:当一个函数(假设我们称其为A)内部调用了它自己或者另一个函数(假设我们称其为B,而B又调用了A,形成了递归),每次函数调用都会将其状态压入调用栈。当递归到达基线条件(Base Case)并开始返回时,每个函数的状态会从栈中弹出,直到最初的调用者得到结果。
队列通常用于实现迭代算法,如广度优先搜索(BFS)等。在BFS中,队列用于存储待处理的节点,并按照它们被添加到队列中的顺序进行处理。这与递归的深度优先搜索(DFS)形成对比,DFS使用栈(或隐式的函数调用栈)来按照后进先出(LIFO)的顺序处理节点。
虽然技术上可以使用队列和显式栈来模拟递归行为(例如,通过迭代实现递归算法),但这样做通常会使代码更复杂,并可能牺牲递归提供的清晰性和简洁性。然而,在某些情况下,例如处理深度非常大的递归树或需要避免栈溢出的场景,使用迭代和显式栈可能是有益的。
2.优先队列用堆来实现
优先队列(Priority Queue)的实现通常选择堆(Heap)作为其底层数据结构,而不是普通队列(Queue)。以下是几个关键原因:
- 数据结构和操作特性:
- 普通队列(Queue)遵循先进先出(FIFO)的原则,即最先进入队列的元素将最先被移除。
- 优先队列(Priority Queue)则允许元素具有优先级,优先级最高的元素将最先被移除,这体现了最高级先出(first in, largest out 或 first in, smallest out,取决于优先级的定义)的行为特征。
- 堆的性质:
- 堆是一种特殊的树形数据结构,它可以被看作是完全二叉树或近似完全二叉树。
- 堆总是满足堆属性:父节点的值总是大于或等于(最大堆)或小于或等于(最小堆)其子节点的值。
- 堆提供了快速访问最大或最小元素(即堆顶元素)的能力,并且可以在对数时间内完成插入和删除操作。
- 实现优先队列:
- 由于堆提供了高效的插入和删除最大/最小元素的操作,因此它非常适合用于实现优先队列。
- 当有新元素需要插入到优先队列中时,可以直接将其插入到堆中,并重新调整堆以保持堆属性。
- 当需要从优先队列中移除最高优先级的元素时,可以直接移除堆顶元素,并重新调整堆。
- 代码示例和设置:
- 在C++的STL(Standard Template Library)中,
priority_queue容器就是一个典型的优先队列实现,其底层就是使用堆。- 通过设置
priority_queue的第三个模板参数(比较类),可以定义队列中元素的优先级。例如,使用greater<int>可以使队列成为小根堆,这样数字小的元素优先级更高;而默认是大根堆,数字大的元素优先级更高。综上所述,优先队列通常使用堆作为其底层数据结构,以提供高效的插入和删除最高/最低优先级元素的操作。
3.当上下限表达式相等时,我们使用下列哪种表示法来描述算法代价?
Θ表示法(Theta notation)用于描述算法的紧确界限,即它同时表示了算法的上限和下限复杂度。当算法的上下限复杂度相同时,Θ表示法是最合适的。
相关文章:

算法 | 刷题日记
1.递归通常是用栈来实现的 递归在其本质上是通过函数调用栈(Call Stack)来实现的,而不是队列(Queue)。当你调用一个函数时,该函数的局部变量、参数和返回地址会被压入(push)到一个由…...

微信小程序登录接口
微信小程序登录,实现思路分析: 用户触发登录操作:用户在微信小程序中点击“登录”按钮,触发登录流程。调用微信登录接口:小程序端调用微信提供的登录接口(如wx.login),获取临时登录…...
(5):介绍一种排列组合算法)
VBA实战(Excel)(5):介绍一种排列组合算法
1. 需求场景 有多个条件,条件个数不定,每个条件有若干种情况,情况个数不定,输出所有条件可能的情况的排列组合。 2.举例 假设第一次有5个情况要填,第一个条件20种情况,第二个5种,第三个40种&…...

迭代器的使用
参考: 生成器迭代器next函数 迭代器的使用 说到迭代器就必须先要提一下可迭代对象(iterable),可迭代对象是能够逐一返回其成员项的对象。可迭代对象包括序列类型(如list、str、tuple)和非序列类型&#…...

安卓手机APP开发___广播概述
安卓手机APP开发___广播概述 目录 概述 关于系统广播 系统广播所发生的更改 接收广播 清单声明的接收器 上下文注册的接收器 对进程状态的影响 发送广播 通过权限限制广播 带权限的发送 带权限的接收 安全注意事项和最佳做法 概述 Android 应用可以通过 Android …...

【封装】Unity切换场景不销毁物体
在切换场景时,如果物体不需要销毁,可以直接使用下方脚本 代码 public class DontDestroyLoader : MonoBehaviour{ //所有不销毁的物体预制体[SerializeField] private GameObject[] dontDestroyPrefabs;//实例化预制体public void Load(){foreach (var …...

基于学习的决策树
基于学习的决策树概述 决策树是一种监督学习方法,广泛应用于分类和回归任务中。基于学习的决策树模型通过学习数据中的特征来构建树状结构,帮助做出决策。以下是对基于学习的决策树的详细介绍,包括其基本概念、工作流程、构建算法、优势和挑…...

godot.bk2
1.$node_name 其实 就是 get_node 的语法糖 2.场景内部用get_node,场景外部用信号 这是自定义信号的绑定,如果是内置信号,直接右键点击链接到一个函数即可 3.场景切换和摄像头一直居中 4.class_name命名一个类,extends继承&…...

STM32 IIC 使用 HAL 库操作eeprom
在STM32上通过I2C接口(注意:在标准STM32库中,I2C接口通常被写为"I2C"而不是"IIC")与EEPROM芯片通信时,你需要遵循I2C通信协议,并使用STM32的HAL库或标准外设库(如果适用&am…...
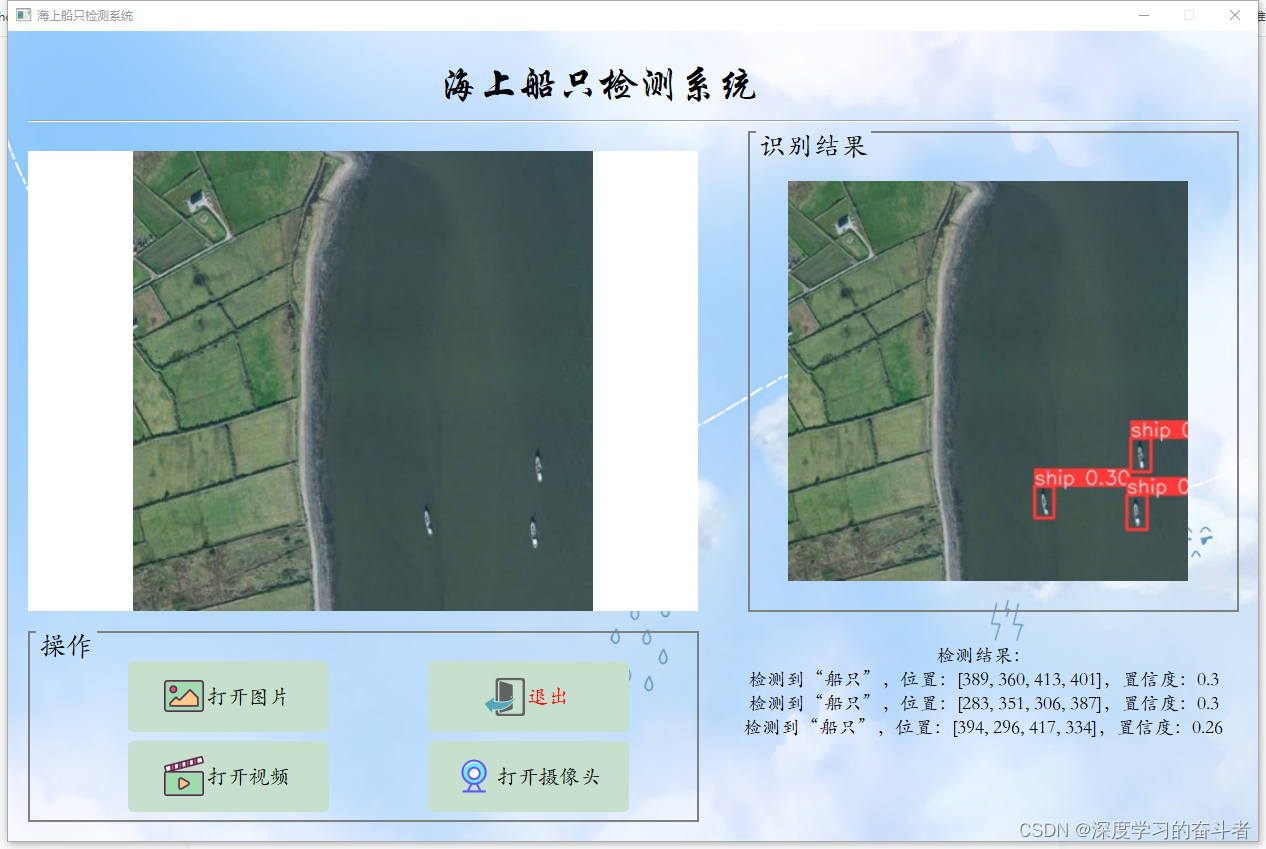
YOLOv8+PyQt5海洋船只检测(可以重新训练,yolov8模型,从图像、视频和摄像头三种路径识别检测)
1.效果视频:海洋船只检测yoloV8检测(https://mbd.pub/o/bread/mbd-ZpaYk55r)_哔哩哔哩_bilibili资源包含可视化的海洋船只检测系统,可对于高空拍摄到的海洋图片进行轮船检测,基于最新的YOLOv8训练的海洋船只检测模型&a…...

PCL 高阶多项式曲线回归拟合(二维)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 高阶多项式曲线回归(Polynomial Regression)是一种线性回归模型的扩展,它允许数据拟合一个非线性的曲线。虽然多项式本身是非线性的,但我们可以通过引入新的变量(例如,原始变量的平方、立方等)来将问题转化为…...

深入理解 Python3 函数:从基础语法到高级应用
Python3 函数是构建模块化代码的基本单位,允许我们将代码组织成独立的、可重用的块。本文将详细介绍 Python3 函数的基本语法、常用命令、示例、应用场景、注意事项,并进行总结。 基本语法 在 Python 中,函数的定义使用 def 关键字…...
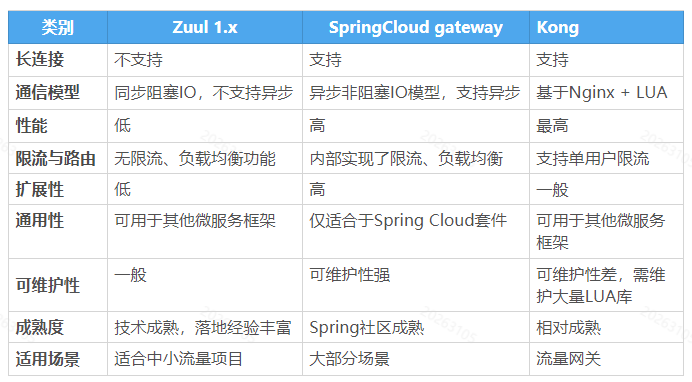
03_初识Spring Cloud Gateway
文章目录 一、网关简介1.1 网关提出的背景1.2 网关在微服务中的位置1.3 网关的技术选型1.4 补充 二、Spring Cloud Gateway的简介2.1 核心概念:路由(Route)2.2 核心概念:断言(Predicate)2.3 核心概念&#…...
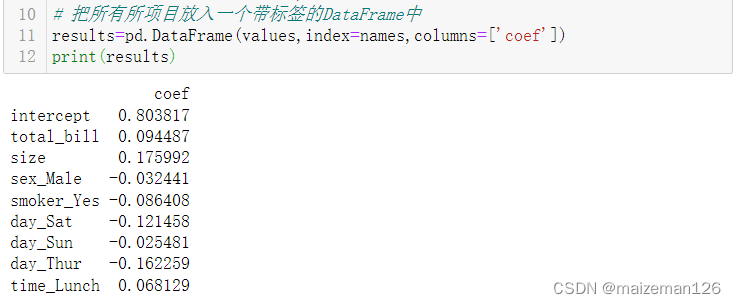
python数据分析——线性模型
参考资料:活用pandas库 1、简单线性回归 线性回归的目标是描述响应变量(或“因变量”)和预测变量(也称“特征”、“协变量”、“自变量”)之间的直线关系。本例中将讨论tips数据集中的total_bill对tip的影响。 # 导入…...

网络原理——HTTP/HTTPS ---- HTTPS
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 目录 HTTPS加密与解密HTTPS的工作流程使用对称密钥来加密使用非对称密钥 来对 对称密钥进行加密第三方公证总结 HTTPS https本质上就是在http的基础之上 增加了加密层,抛开加密层之后,剩下的部…...
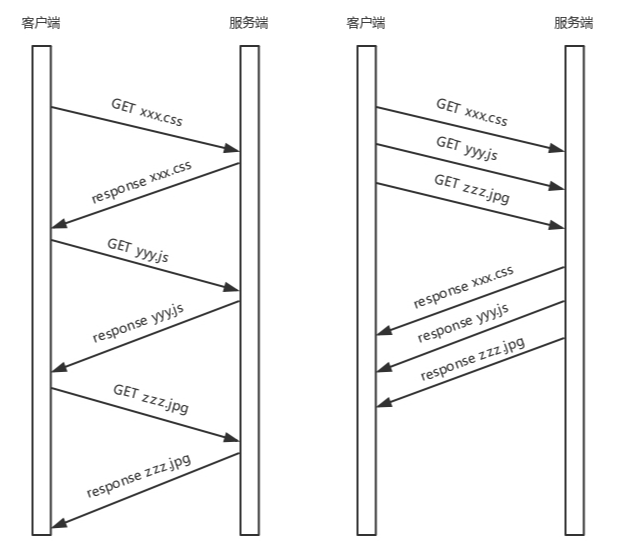
网络协议二
一、套接字Socket 基于 TCP UDP 协议的 Socket 编程,在讲 TCP 和 UDP 协议的时候,我们分客户端和服务端,在写程序的时候,我们也同样这样分。 在网络层,Socket 函数需要指定到底是 IPv4 还是 IPv6,分别对应设…...

内存映射mmap技术详解
一、mmap基础概念 mmap 即 memory map,也就是内存映射。mmap 是一种内存映射文件的方法,即将一个文件或者其它对象映射到进程的地址空间,实现文件磁盘地址和进程虚拟地址空间中一段虚拟地址的一一对映关系。实现这样的映射关系后,…...

react 合成事件
React合成事件-CSDN博客 当然,很高兴为你解释React中的合成事件概念,非常适合React初学者理解。 想象一下,你正在组织一场派对,为了让派对顺利进行,你需要管理各种活动,比如游戏、音乐和食物分配。但是&a…...
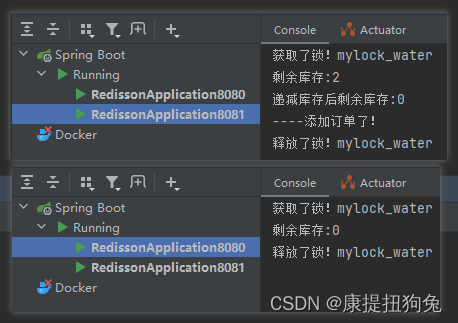
springboot配置集成RedisTemplate和Redisson,使用分布式锁案例
文章要点 自定义配置属性类集成配置RedisTemplate集成配置分布式锁Redisson使用分布式锁简单实现超卖方案 1. 项目结构 2. 集成RedisTemplate和Redisson 添加依赖 依赖的版本与继承的spring-boot-starter-parent工程相对应,可写可不写 <!--spring data redis…...

随机数相关
产生随机数对象 固定写法: Random 随机数变量名 new Random();Random r new Random();生成随机数 int i r.Next(); //生成一个非负数的随机数 Console.WriteLine(i);i r.Next(100); // 生成一个 0~99的随机数 左边始终是0 左包含 右边是100 右不包含 Consol…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
