tinyrenderer-切线空间法线贴图
法线贴图
法线贴图分两种,一种是模型空间中的,一种是切线空间中的

模型空间中的法线贴图的rgb代表着每个渲染像素法线的xyz,与顶点坐标处于一个空间,图片是五颜六色的。

切线空间中的法线贴图的rgb同样对应xyz,是切线空间里的坐标,切线空间里的z轴正向垂直与当前三角形便宜,x是当前三角形片元表面的一个切线,y是他们的叉积。
切线空间每个轴范围是-1到1.但图片本身0-255对应的是0-1.而多数法线都是都是(0,0,1)(即当前像素的法向量刚好就是当前片元的顶点法向量)转换到颜色空间就是(0.5,0.5,1)(法向量坐标可能为负,但颜色范围始终为正)。因此图片主要是蓝紫色
两个完全一样材质的物体,由于位置不同光照也会不同。如果用模型空间存储的法线贴图,是绝对法线,法向量会完全不同,无法使用同一张物体。而切线空间存储的法线贴图完全是基于物体自身的,是相对法线,多个物体可以复用(优点)。但再实际计算时,需要根据物体本身的缩放位移做相应的矩阵转换处理(缺点)
模型空间的法线贴图直接提取向量信息做为法线向量即可
Vec3f Model::getNormal(float x, float y) {TGAColor n = normalTex_.get(x * normalTex_.get_width(), y * normalTex_.get_height());Vec3f res;for (int i = 0; i < 3; i++) {res[i] = n.bgra[i] / 255.f * 2 - 1.f;}return res;
}
//....
struct normalTexShader :public IShader {mat<2, 3, float> uv;virtual Vec4f vertex(int iface, int vertIdx, Matrix mvp) {Vec3f v = model->vert(model->face(iface)[vertIdx]);uv.set_col(vertIdx, model->tverts(model->tface(iface)[vertIdx]));return mvp * embed<4>(v);}virtual bool fragment(Vec3f barycentricCoordinates, TGAColor& color) {Vec2f texcoords = uv * barycentricCoordinates;Vec3f normal = model->getNormal(texcoords.x, texcoords.y);float I = std::max(0.f, normal * light_dir);color = model->getDiffuseColor(texcoords.x, texcoords.y) * I;return false;}
};

切线空间的法线贴图使用,重点求出tbn矩阵,将切线空间的法线转化到世界空间中
tbn矩阵
tbn矩阵
tbn矩阵
当tbn矩阵的n是模型空间时,法线贴图取值经过tbn变换后是模型空间法线
当tbn矩阵的n是世界空间时,法线贴图取值经过tbn变换后是世界空间法线
对于三角形表面所有点,t切线和b切线都是相同的

顶点法线与面法线可能不同
面法线只是垂直于面的一条向量,规定了面的正反,而顶点法线才是用于光照信息的处理(建模软件中,顶点法线的最初是的默认情况也并非是面法线的平均,只有当在建模软件中对物体进行了平滑着色后,才会根据面法线平均得到顶点法线)
因此要通过每个顶点的切线找到曲面的法线
struct Shader :public IShader {mat<2, 3, float> uv;Vec3f vp[3];Matrix MVP = rasterizer->getProjection() * rasterizer->getModelView();mat<3, 3, float> n;virtual Vec4f vertex(int iface, int vertIdx) {Vec3f v = model->vert(model->face(iface)[vertIdx]);uv.set_col(vertIdx, model->tverts(model->tface(iface)[vertIdx]));vp[vertIdx] = v;n.set_col(vertIdx, model->nverts(model->nface(iface)[vertIdx]));return MVP * embed<4>(v);}virtual bool fragment(Vec3f barycentricCoordinates, TGAColor& color) {Vec3f N = (n * barycentricCoordinates).normalize();float u1 = uv[0][1] - uv[0][0];float v1 = uv[1][1] - uv[1][0];float u2 = uv[0][2] - uv[0][0];float v2 = uv[1][2] - uv[1][0];Vec3f e1 = vp[1] - vp[0];Vec3f e2 = vp[2] - vp[0];float f = 1.f / (u1 * v2 - u2 * v1);Vec3f T = (e1 * v2 - e2 * v1) * f;T = T - N * (T * N);T.normalize();Vec3f B = cross(N, T).normalize();mat<3, 3, float> TBN;TBN.set_col(0, T);TBN.set_col(1, B);TBN.set_col(2, N);Vec2f texcoords = uv * barycentricCoordinates;Vec3f normal = TBN * model->getNormal(texcoords.x, texcoords.y);float I = std::max(0.f, normal * light_dir);color = model->getDiffuseColor(texcoords.x, texcoords.y) * I;return false;}
};
有一点注意的是,很多文章里的tbn矩阵只到了这步推导公式
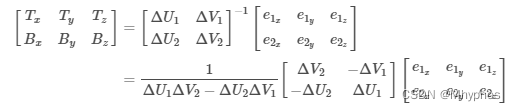
求出了t和b向量后,实际上还要加上N做一次正交化,否则是不保证相互垂直的。最终才是tbn矩阵

项目跟随练习代码地址
相关文章:

tinyrenderer-切线空间法线贴图
法线贴图 法线贴图分两种,一种是模型空间中的,一种是切线空间中的 模型空间中的法线贴图的rgb代表着每个渲染像素法线的xyz,与顶点坐标处于一个空间,图片是五颜六色的。 切线空间中的法线贴图的rgb同样对应xyz,是切线…...
C++的vector使用优化
我们在上一章说了如何使用这个vector动态数组,这章我们说说如何更好的使用它以及它是如何工作的。当你创建一个vector,然后使用push_back添加元素,当当前的vector的内存不够时,会从内存中的旧位置复制到内存中的新位置,…...

关于stm32的复用和重映射问题
目录 需求IO口的复用和重映射使用复用复用加重映射 总结参考资料 需求 一开始使用stm32c8t6,想实现pwm输出,但是原电路固定在芯片的引脚PB10和PB11上,查看了下引脚的功能,需要使用到复用功能。让改引脚作为定时器PWM的输出IO口。…...

遍历数组1
package demo; import java.util.ArrayList; public class Arrilist { public static void main(String[] args) { ArrayList<String>listnew ArrayList<>(); list.add("汤神"); list.add("yyx"); list.add("hong go…...

Go语言 一些问题了解
一、读取文件数据,是阻塞还是非阻塞的? 分两种情况:常规读取文件数据,和网络IO读取数据 1. 常规读取文件数据: io.Reader 和 bufio.Reader 是阻塞进行的。 bufio.Reader 提供缓冲的读取操作,意味着数据是…...

C++ Primer 第五版 第15章 面向对象程序设计
面向对象程序设计基于三个基本概念:数据抽象、继承和动态绑定。 继承和动态绑定对编写程序有两方面的影响:一是我们可以更容易地定义与其他类相似但不完全相同的新类;二是在使用这些彼此相似的类编写程序时,我们可以在一定程度上…...
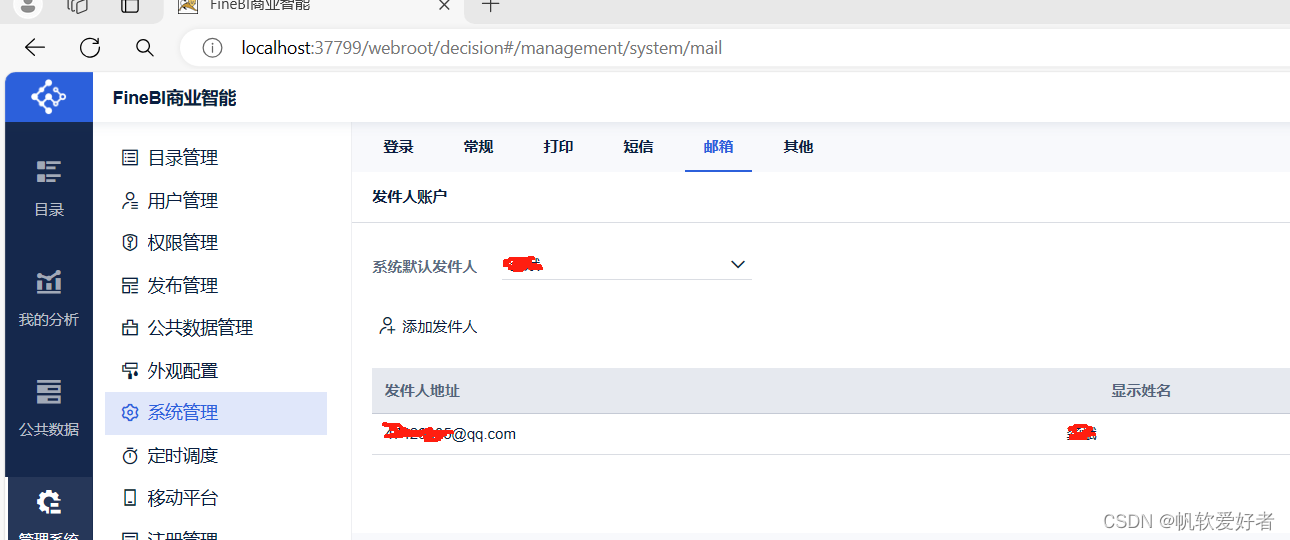
finebi或者finereport发邮件
我们二次开发中,如果想利用产品自带的发邮件的功能,来发送自己的邮件内容。 首先 决策系统中邮件相关信息要配置好之后: 这里配好了发件人,以及默认发件人后, private void sendEmail(String content,String subject)…...

基于聚类和回归分析方法探究蓝莓产量影响因素与预测模型研究
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 目录 背景数据说明数据来源思考 正文数据预处理数据读取数据预览数据处理 相关性分析聚类分析数据处理确定聚类数建立k均值聚类模型 多元线性回…...

【数据结构】从前序与中序遍历,或中序与后序遍历序列,构造二叉树
欢迎浏览高耳机的博客 希望我们彼此都有更好的收获 感谢三连支持! 首先,根据先序遍历可以确定根节点E,再在中序遍历中通过E确定左树和右数 ; 设立inBegin和inEnd,通过这两个参数的游走,来进行子树的创建&a…...

ARM公司发展历程
Arm从1990年成立前开始,历经漫长岁月树立各项公司里程碑及产品成就,一步步成为全球最普及的运算平台。 添加图片注释,不超过 140 字(可选) Acorn 时期 1978年,Chris Curry和Hermann Hauser共同创立了Acorn…...

C# :IQueryable IEnumerable
文章目录 1. IEnumerable2. IQueryable3. LINQ to SQL4. IEnumerable & IQueryable4.1 Expression4.2 Provider 1. IEnumerable namespace System.Collections: public interface IEnumerable {public IEnumerator GetEnumerator (); }public interface IEnumerator {pubi…...

三、生成RPM包
文章目录 1、编译生成so、bin 通过此工程编译生成so\bin文件 2、将so\bin打包到rpm中 ###### 1.生成可执行文件、库文件 ######### cmake_minimum_required(VERSION 3.15)project(compute) set(target zls_bin) set(target2 libcompute.so) # 依赖的头文件 include_directori…...

单实例11.2.0.4迁移到11.2.0.4RAC_使用rman异机恢复
保命法则:先备份再操作,磁盘空间紧张无法备份就让满足,给自己留退路。 场景说明: 1.本文档的环境为同平台、不同版本(操作系统版本可以不同,数据库版本相同),源机器和目标机器部分…...
)
MySQL之查询性能优化(二)
查询性能优化 慢查询基础:优化数据访问 查询性能低下最基本的原因是访问的数据太多。某些查询可能不可避免地需要筛选大量数据,但这并不场景。大部分性能低下的查询都可以通过减少访问的数据量的方式进行优化。对于低效的查询,我们发现通过下面两个步骤…...

The Best Toolkit 最好用的工具集
The Best Toolkit 工欲善其事,必先利其器,整理过往工作与生活中遇到的最好的工具软件 PDF合并等 PDF24 Tools PDF查看器 SumatraPDF 可以使用黑色来查看,相对不伤眼睛,也有电子书相关的阅读器 Kindle pdf裁边工具 briss 软件卸载…...
类型)
使用C#反射中的MAKEGENERICTYPE函数,来为泛型方法和泛型类指定(泛型的)类型
MakeGenericType 是一个在 C# 中用于创建开放类型的实例的方法。开放类型是一种未绑定类型参数的泛型类型。当你有一个泛型类型定义,并且想要用特定的类型实例化它时,你可以使用 MakeGenericType 方法。 public Type MakeGenericType (params Type[] ty…...

sql注入 (运用sqlmap解题)
注:level参数 使用–batch参数可指定payload测试复杂等级。共有五个级别,从1-5,默认值为1。等级越高,测试的payload越复杂,当使用默认等级注入不出来时,可以尝试使用–level来提高测试等级。 --level 参数决定了 sql…...

HTML5 Canvas 绘图教程二
在本教程中,我们将探讨 canvas 的高级用法,包括复杂的绘图 API、坐标系统和变换操作、平滑动画技术以及复杂应用和游戏开发的实践。 1. 绘图 API 高级方法 1.1 二次贝塞尔曲线 (quadraticCurveTo) 二次贝塞尔曲线需要两个点:一个控制点和一…...

Linux 命令 find 的深度解析与使用
Linux 命令 find 的深度解析与使用 在 Linux 系统中,find 命令是一个功能强大的工具,用于在文件系统中搜索文件或目录。无论是基于文件名、文件类型、文件大小、文件权限,还是基于文件的最后修改时间等,find 命令都能提供灵活的搜…...

字符串操作记录
1 拼接 Concat():拼接字符串 Let stringvalue “hello ”; Let result stringvalue.concat(“world”) Console.log(result) // “hello world” 2 删 Let stringvalue “hello world”Console.log(stringvalue.slice(3)); // ‘lo world’Console.log(stringvalue.subst…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
