双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题:
两数之和II—输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6 输出:[1,3] 解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1 输出:[1,2] 解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2]
思路:
双指针的思想,nums是一个有序的数组 因此我们可以使用这个特性,即数据从小到大递增,创建连个指针left指向0,right指向数组末尾 若它们所指向的数据和为target,直接返回 ;否则若值小于target,则left++ 否则 right--;
public int[] twoSum(int[] numbers, int target) {int left=0,right=numbers.length-1;while(left<right){int sum=numbers[left]+numbers[right];if(sum==target)return new int []{left+1,right+1};else if(sum<target)left++;elseright--;}return new int[0];
}
盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
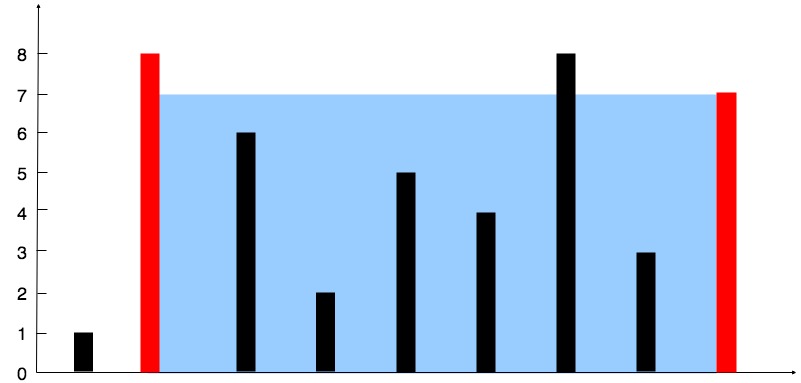
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
思路:
最笨方法就是暴力解法:就是经过两次循环计算出所有的储水量,找出其中最大的并返回。但可能会超时
在这里我们可以使用双指针,left指向0,right指向height.length-1; 初始化res=0,表示当前的盛水量,使用Math.min(height[left],height[right])*(right-left)来计算盛水量,=并与res进行比较将较大真存在res中,然后移动left或right :若height[left]<=height[right],就left++ 否则right--(是因为每次都是有Math.min来计算,所以移动较短的哪一方,若移动较长的哪一方,盛水量肯定减少)直到left>=right
public int maxArea(int[] height) {int left=0,right=height.length-1;int res=0;while(left < right){int k=Math.min(height[left],height[right])*(right-left);if(k>res)res=k;if(height[left]<=height[right])left++;elseright--;}return res;
}三数之和
在看三数之和之前,可以看看两数之和
两数之和:
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
思路:
第一种:暴力解法 ,循环求解
public int[] twoSum(int[] nums, int target) {for(int i=0;i<nums.length;i++){for(int j=i+1;j<nums.length;j++){if(nums[i]+nums[j]==target)return new int []{i,j};}}return new int [0];
}第二种:哈希算法
创建一个hashmap存储数据和其对应的下标,刚开始时hashmap为空,循环遍历数组for(int i=0;i<nums.length;i++) 若hashmap中包含target-nums[i] 则返回其下标和i 否则就将其加入到hashmap中(这里我刚开始不懂,此时hashmap为空怎么去寻找数据?为target是由两数在组成的,比如9=2+7,第一次访问2,map中找不到7,将2加入到map中,当访问7时就可以在map中找到2 )
public int[] twoSum(int[] nums, int target) {hashMap<Integer> map=new HashMAp<>();for(int i=0;i<nums.length;i++){if(map.containsKey(target-nums[i]){return new int[]{map.get(target-nums[i],i};hashmap.put(nums[i],i);}return new int nums[0];
}三数之和解题
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
思路:
1、将三数之和变成一个数固定的两数之和
2、如何保证元素不重复??
首先需要对数组进行排序Ayyays.sort(nums),这样就变成不递减的数组
然后在进行遍历的过程中需要注意 此时遍历的数不能和它的前面一个数相同

最后可以借鉴有序数组的两数之和进行寻找
public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> list=new AyyayList<List<Integer>>();int first=0;Arrays.sort(nums); // 进行排序for(first=0;first<nums.length;first++){//固定第一个数if(first>0 && nums[first]==nums[first-1]) //此时遍历的数不能和它的前面一个数相同,否则会出现重复return continue; int target=0-nums[i]; //其余两数之和int thrid=nums.length-1; //第三个指针指向数组末尾for(int second=first+1; second<nums.length;second++){if(second>first+1 && nums[second]==nums[second-1])continue;while(second<thrid && nums[second]+nums[thrid]>target) //因为此时是从小到大排序的 ,所以当nums[second]+nums[thrid]不大于target就有可能找到那个数了thrid--;if(second==thrid)break;if(nums[second]==nums[thrid]){List<Integer> res=new AyyayList<>();res.add(nums[first]);res.add(nums[second]);res.add(nums[thrid]);list.add(res);}}}return list;
}
相关文章:

双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题: 两数之和II—输入有序数组 给你一个下标从 1 开始的整数数组 numbers ࿰…...
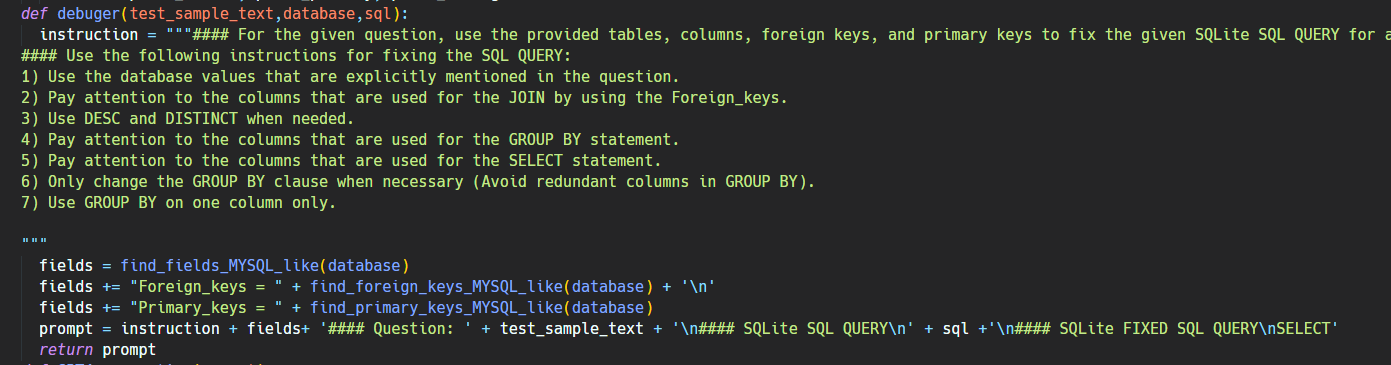
【Text2SQL 论文】DIN-SQL:分解任务 + 自我纠正 + in-context 让 LLM 完成 Text2SQL
论文:DIN-SQL: Decomposed In-Context Learning of Text-to-SQL with Self-Correction ⭐⭐⭐⭐ NeurIPS 2023, arXiv:2304.11015 Code: Few-shot-NL2SQL-with-prompting | GitHub 文章目录 一、论文速读1.1 Schema Linking Module1.2 Classification & Decompo…...

基于Springboot+vue实现的汽车服务管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

ROS2从入门到精通4-3:全局路径规划插件开发案例(以A*算法为例)
目录 0 专栏介绍1 路径规划插件的意义2 全局规划插件编写模板2.1 构造规划插件类2.2 注册并导出插件2.3 编译与使用插件 3 全局规划插件开发案例(A*算法)常见问题 0 专栏介绍 本专栏旨在通过对ROS2的系统学习,掌握ROS2底层基本分布式原理,并具有机器人建…...
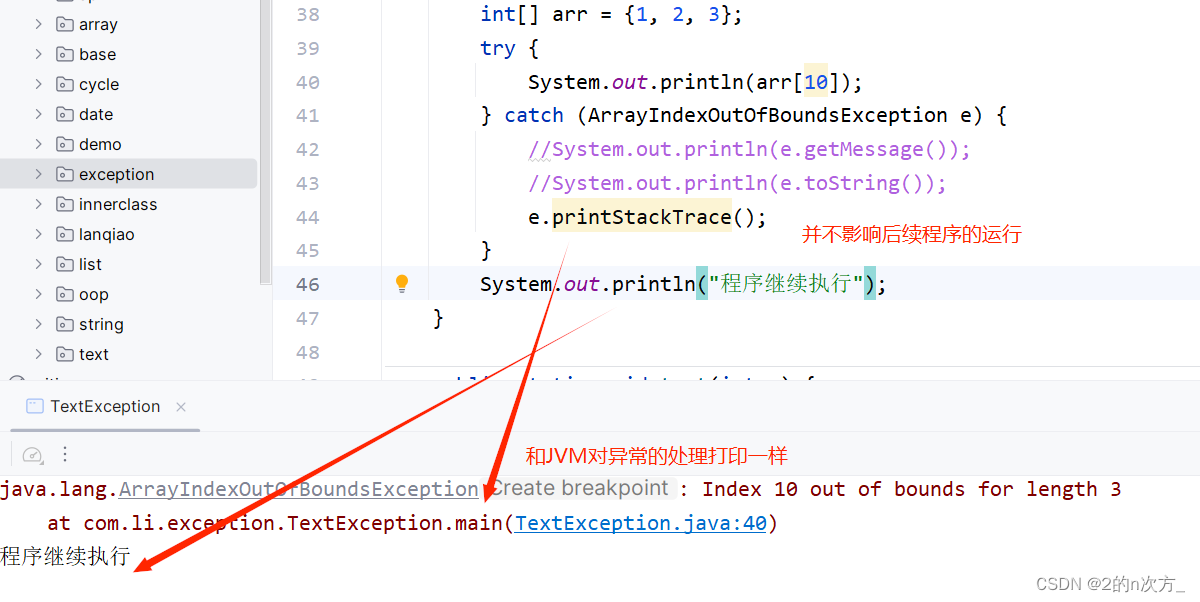
Java学习【认识异常】
Java学习【认识异常】 认识异常异常的种类异常的作用 异常的处理方式JVM默认的处理方式捕获异常finally 多个异常的处理异常中的方法抛出异常 自定义异常 认识异常 在Java中,将程序执行过程中发生的不正常行为称为异常 异常的种类 Error代表的是系统级别的错误&a…...

uniapp+h5 ——微信小程序页面截屏保存在手机
web-view 需要用到 web-view ,类似于iframe, 将网页嵌套到微信小程序中,参数传递等; 示例(无法实时传递数据),页面销毁时才能拿到h5传递的数据,只能利用这点点击跳转到小程序另一个…...
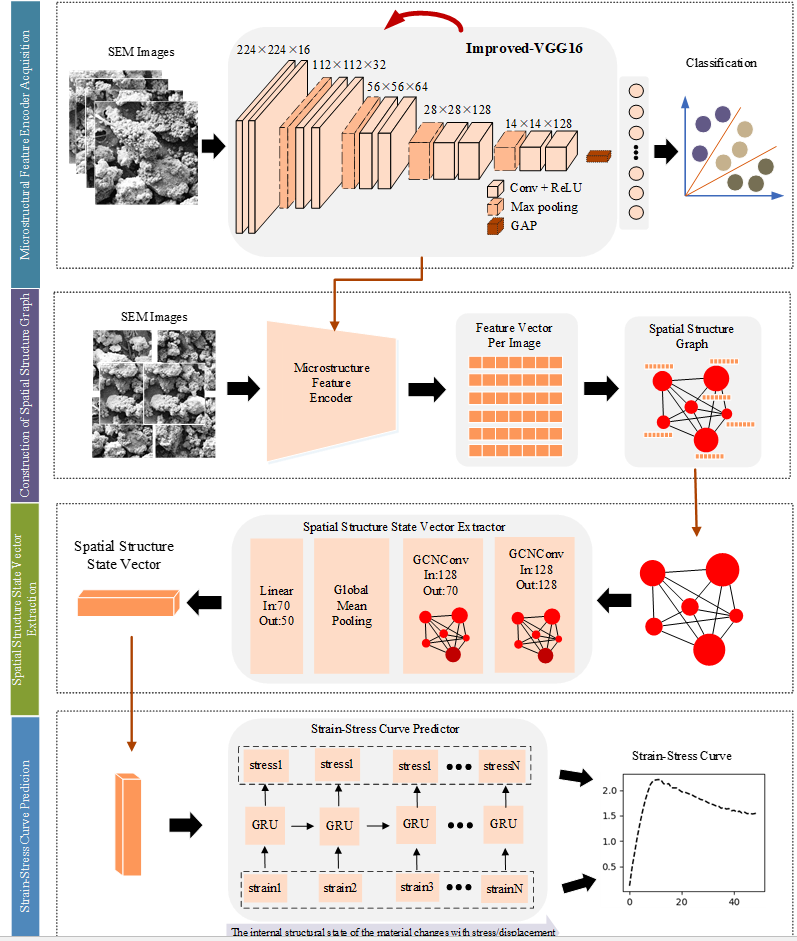
三、基于图像分类预训练编码及图神经网络的预测模型 【框图+源码】
背景: 抽时间补充,先挖个坑。 一、模型结构 二、源码...
Linux - 高级IO
目录 理解五种IO模型非阻塞IO的设置多路转接之select 实现一个简易的select服务器select服务器的优缺点 多路转接之poll 实现一个简易的poll服务器poll服务器的优缺点 多路转接之epoll epoll原理epoll的优势用epoll实现一个简易的echo服务器 epoll的LT和ET工作模式 什么是LT和…...

面试题:说一下 http 报文都有哪些东西?
面试题:说一下 http 报文都有哪些东西? HTTP 是传输超文本(实际上除了 HTML,可以传输任何类型的文件,如视频、音频、文本等)的协议,是一组用于浏览器-服务器之间数据传输的规则。 HTTP 位于 OS…...
开山之作!Python数据与算法分析手册,登顶GitHub!
若把编写代码比作行军打仗,那么要想称霸沙场,不能仅靠手中的利刃,还需深谙兵法。 Python是一把利刃,数据结构与算法则是兵法。只有熟读兵法,才能使利刃所向披靡。只有洞彻数据结构与算法,才能真正精通Pyth…...

编译安装gcc-11及可能遇到的bug
编译安装脚本 GCC_VERSION11.1.0 PACKAGE_DIR/path/to/gcc/source/code GCC_DIR$PACKAGE_DIR/gcc-$GCC_VERSION GCC_INSTALL_DIR/path/to/install/gccmkdir -p $GCC_INSTALL_DIR cd $GCC_INSTALL_DIR rm -rf * cd $PACKAGE_DIR rm -rf gcc-$GCC_VERSION if [ ! -f "gcc-$…...

vue项目引入json/js文件批量或单个方法
vue项目 json // 方式一 : 将文件内容完整的引入 import json from ./src/assets/xxx.json console.log(json) console.log(---)// 方式二 : 部分引入-名称必须是文件中定义的key import {name1,name2} from ./src/assets/xxx.json console.log(name1)…...
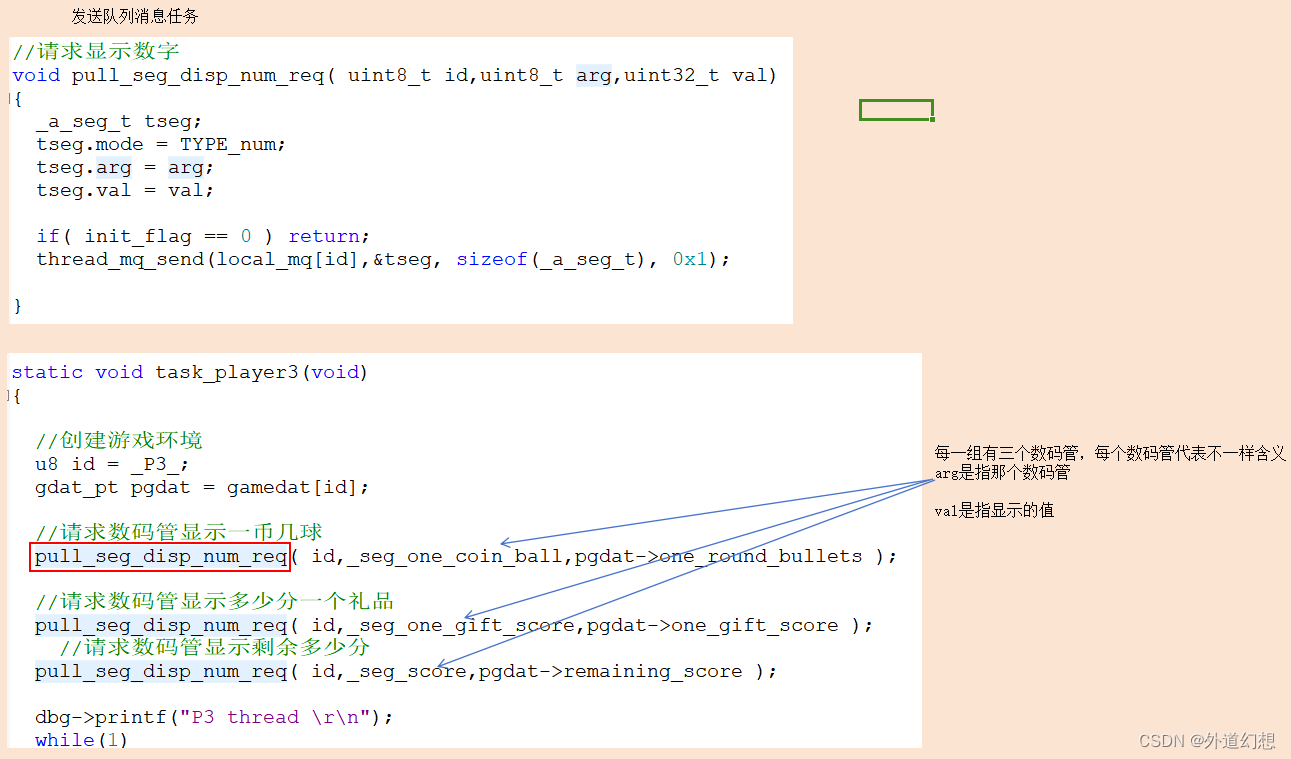
守护任务用来防止资源冲突
背景:有三个任务,他们都需要操作数码管。每个任务对应三个数码管,共9个数码管。硬件上9个数码管的控制使用一套硬件完成。 策略:每个任务都往自己的队列里面发数据,单独建立一个监听任务:处理所有队列的数…...

fast admin实现多数据库导入数据
思路 1创建多数据库连接 2后端的前台代码能使用get或者post请求传递选中数据给后台 3后台能够接收到 4后台接收到id或者全字段数据后对数据进行处理,然后使用多数据库操作将其存入第二个数据库 实现 1config文件下创建新数据库连接 db_config2 > [// 数据库类…...

NLP基础——序列模型(动手学深度学习)
序列模型 定义 序列模型是自然语言处理(NLP)和机器学习领域中一类重要的模型,它们特别适合处理具有时间顺序或序列结构的数据,例如文本、语音信号或时间序列数据。 举个例子:一部电影的评分在不同时间段的评分可能是…...

机器学习AI大模型的开源与闭源:哪个更好?
文章目录 前言一、开源AI模型1.1 开源的优点1.2 开源的缺点 二、闭源AI模型2.1 闭源的优点2.2 闭源的缺点 三、开源与闭源的平衡3.1 开源与闭源结合的案例3.2 开源与闭源的战略选择 小结 前言 在过去的几年里,人工智能(AI)和机器学习…...

关于大模型多轮问答的两种方式
前言 大模型的多轮问答难点就是在于如何精确识别用户最新的提问的真实意图,而在常见的使用大模型进行多轮对话方式中,我接触到的只有两种方式: 一种是简单地直接使用 user 和 assistant 两个角色将一问一答的会话内容喂给大模型,…...

达梦数据库相关SQL及适配Mysql配置总结
🍓 简介:java系列技术分享(👉持续更新中…🔥) 🍓 初衷:一起学习、一起进步、坚持不懈 🍓 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正🙏 🍓 希望这篇文章对你有所帮助,欢…...

Centos7.9实现多台机器ssh免密登录
1.本机(172.16.10.228)先生成密钥对 ssh-keygen -t rsa 2.执行命令,把本机公钥拷贝到远程机器 ssh-copy-id rootdistinctIp 3.查看一下远程机器 、/root/.ssh/authorized_keys文件 cat /root/.ssh/authorized_keys 会看到里边多了个公钥…...

Unity3D DOTS JobSystem物理引擎的使用详解
前言 Unity3D DOTS(Data-Oriented Technology Stack)是Unity引擎的一项新技术,旨在提高游戏性能和扩展性。其中的Job System是一种用于并行处理任务的系统,可以有效地利用多核处理器的性能。在本文中,我们将重点介绍如…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
