【高阶数据结构(八)】跳表详解
💓博主CSDN主页:杭电码农-NEO💓
⏩专栏分类:高阶数据结构专栏⏪
🚚代码仓库:NEO的学习日记🚚
🌹关注我🫵带你学习更多数据结构
🔝🔝

高阶数据结构
- 1. 前言
- 2. 跳表的概念
- 3. 跳表的特性分析
- 4. 跳表的效率分析
- 5. 跳表模拟实现
- 7. 跳表和传统查找结构的对比
- 8. 总结
1. 前言
跳表也是一种查找结构,和红黑树,哈希的价值是一样的,那么跳表的优势是什么呢?
本章重点:
本篇文章会着重讲解跳表的基本概念和特性, 讲解实现跳表的逻辑,以及手撕一个跳表. 最后会将跳表和红黑树/哈希进行对比, 分析优势和缺点
2. 跳表的概念
跳表是基于有序链表的基础上发展而来的

有序链表的查找效率为O(N). 优化策略:
- 假如每相邻两个节点升高一层,增加一个指针,让指针指向下下个节点,如图b。这样所有新增加的指针连成了一个新的链表,但它包含的节点个数只有原来的一半。由于新增加的指针,我们不再需要与链表中每个节点逐个进行比较了,需要比较的节点数大概只有原来的一半

- 以此类推,我们可以在第二层新产生的链表上,继续为每相邻的两个节点升高一层,增加一个指针,从而产生第三层链表。如下图c,这样搜索效率就进一步提高了。

- 跳表正是受这种多层链表的想法的启发而设计出来的。这样设计确实可以大大提高效率,但问题是,一旦此结构进行插入或删除, 整个跳表的规则就会被打乱. 插入/删除一个元素后, 后面节点的高度可能就不符合跳表的规则了.
跳表的发明者为了避免上诉情况,设计了这样的一种结构:
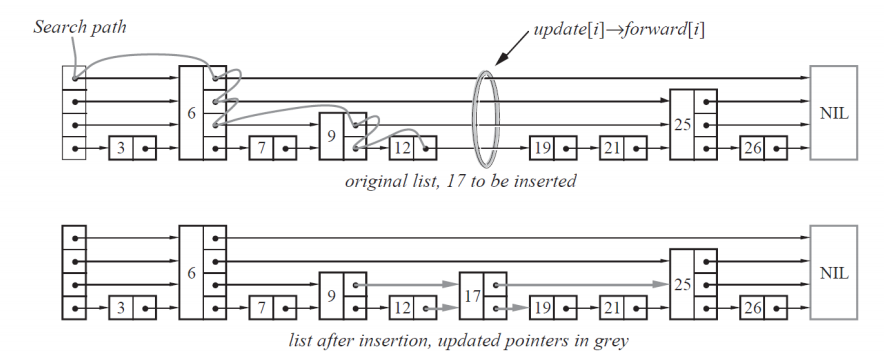
- skiplist的设计为了避免这种问题,做了一个大胆的处理,不再严格要求对应比例关系,而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数,这样就好处理多了
3. 跳表的特性分析
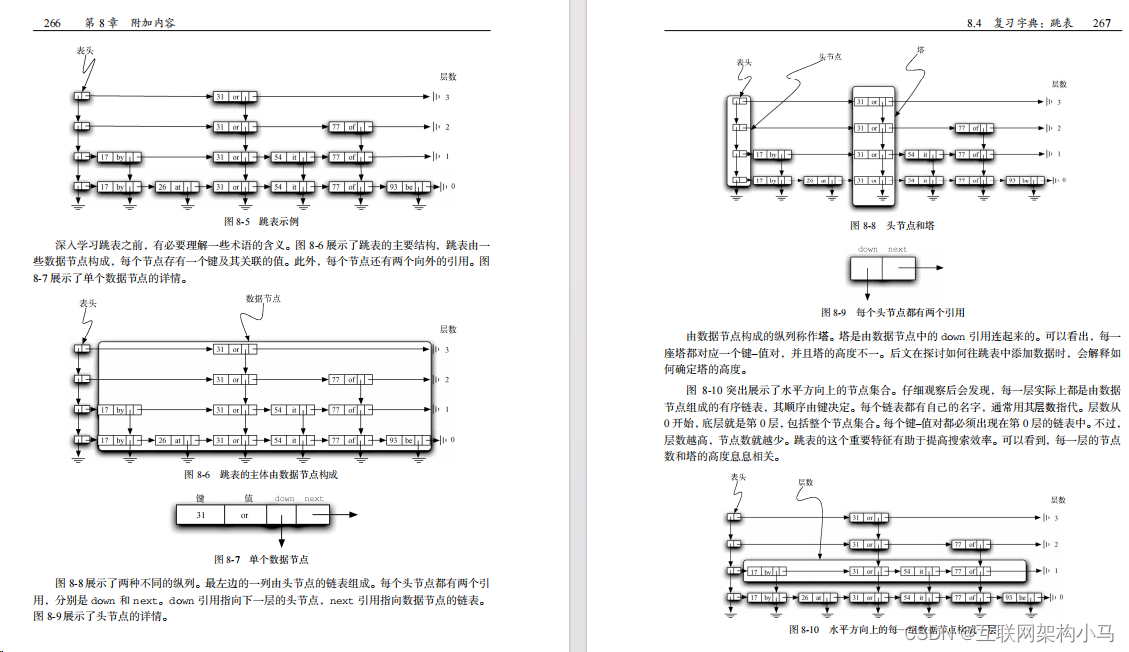
拿下图举例:

查找19分析:
从头节点的最上面的节点开始, next=6,19大于6.直接向右跳到6. next=空,向下走,next=25.25大于19.再向下走. next=9.19大于9,向右走到9. next=17. 19大于17, 向右跳到17. next=25. 25大于19.向下走. next=19.找到19.
总结: 比它大, 向右走. 比它小, 向下走
插入/删除分析:
插入和删除操作的关键都是, 找到此位置的每一层节点的前一个和后一个节点. 插入和删除和其他节点无关, 只需要修改每一层的next指针指向即可. 比如现在要在节点7和9之间插入节点8. 节点8假设是三层. 那么插入只需要考虑节点8的第一层和第二层的前一个节点是6,而第三层的前一个节点是7. 第一层的后一个节点是25.第二层的后一个节点是9.第三次的后一个节点也是9. 依次改变指针知晓即可.
4. 跳表的效率分析
上面我们说到,skiplist插入一个节点时随机出一个层数,听起来怎么这么随意,如何保证搜索时
的效率呢?这里首先要细节分析的是这个随机层数是怎么来的。一般跳表会设计一个最大层数maxLevel的限制,其次会设置一个多增加一层的概率p。那么计算这个随机层数的伪代码如下图:

p代表概率,maxlevel代表最高层数
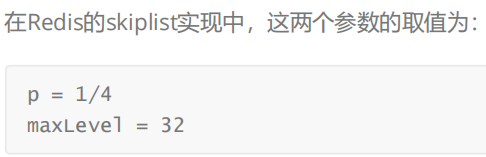
根据前面randomLevel()的伪码,我们很容易看出,产生越高的节点层数,概率越低。定量的分析如下:
- 节点层数至少为1。而大于1的节点层数,满足一个概率分布。
- 节点层数恰好等于1的概率为
1-p。 - 节点层数大于等于2的概率为p,而节点层数恰好等于2的概率为
p(1-p)。 - 节点层数大于等于3的概率为p^ 2,而节点层数恰好等于3的概率为
p^2*(1-p)。 - 节点层数大于等于4的概率为p^ 3,而节点层数恰好等于4的概率为
p^3*(1-p)。

综上所述,跳表的平均时间复杂度为: O(logN)
5. 跳表模拟实现
首先是跳表的节点构造:
struct SkipListNode {int _val;vector<SkipListNode*> _nextv;SkipListNode(int val, int height) :_val(val), _nextv(height, nullptr){}
};
链表的多层结构可以抽象为vector, 而每一层的高度在初始化此节点时再使用随机算法来计算. 这里我们设置p为0.5,maxlevel为32. 写死它,当然后续你也可以做拓展
跳表的增删查改:
class Skiplist {typedef SkipListNode node;
public:Skiplist() {//头节点层数先给1层_head = new node(-1, 1);srand(time(0));}bool search(int target) {node* cur = _head;int level = _head->_nextv.size() - 1;while (level >= 0){//和cur->next[level]比较,比它小就向下走,比它大向右走if (cur->_nextv[level] && cur->_nextv[level]->_val < target)cur = cur->_nextv[level];//下一个节点是空,即是尾,也要向下走else if (!cur->_nextv[level] || cur->_nextv[level]->_val > target)level--;else return true;}return false;}vector<node*> FindPrevNode(int num){node* cur = _head;int level = _head->_nextv.size() - 1;vector<node*> prev(level + 1, _head);//用于保存每一层的前一个while (level >= 0){//一旦要向下走了,就可以更新了,向右走不需要动if (cur->_nextv[level] && cur->_nextv[level]->_val < num)cur = cur->_nextv[level];else if (cur->_nextv[level] == nullptr || cur->_nextv[level]->_val >= num){prev[level] = cur;--level;}}return prev;}void add(int num) {vector<node*> prev = FindPrevNode(num);int n = RandomLevel();node* newnode = new node(num, n);if (_head->_nextv.size() < n){_head->_nextv.resize(n, nullptr);prev.resize(n, _head);}//链接前后节点即可for (int i = 0; i < n; i++){//新节点的下一个是prev的下一个newnode->_nextv[i] = prev[i]->_nextv[i];prev[i]->_nextv[i] = newnode;}}bool erase(int num) {//要删除你,先找到此节点的每层的前一个,和插入时相似vector<node*> prev = FindPrevNode(num);//代表这个值不存在, 最下层找不到它,它就一定不存在if (prev[0]->_nextv[0] == nullptr || prev[0]->_nextv[0]->_val != num)return false;node* del = prev[0]->_nextv[0];for (int i = 0; i < del->_nextv.size(); i++)prev[i]->_nextv[i] = del->_nextv[i];delete del;return true;}int RandomLevel(){int level = 1;while (rand() < RAND_MAX * _p && level < _max)level++;return level;}void Print(){int level = _head->_nextv.size();for (int i = level - 1; i >= 0; --i){node* cur = _head;while (cur){printf("%d->", cur->_val);cur = cur->_nextv[i];}printf("\n");}}
private:node* _head;size_t _max = 32;double _p = 0.5;
};
代码的解释都在注释中,不懂欢迎私信
7. 跳表和传统查找结构的对比
-
skiplist相比平衡搜索树(AVL树和红黑树)对比,都可以做到遍历数据有序,时间复杂度也差不多。skiplist的优势是:a、skiplist实现简单,容易控制。平衡树增删查改遍历都更复杂。 b、skiplist的额外空间消耗更低。平衡树节点存储每个值有三叉链,平衡因子/颜色等消耗。skiplist中p=1/2时,每个节点所包含的平均指针数目为2;skiplist中p=1/4时,每个节点所包含的平均指针数目为1.33;
-
skiplist相比哈希表而言,就没有那么大的优势了。相比而言a、哈希表平均时间复杂度是O(1),比skiplist快。b、哈希表空间消耗略多一点。skiplist优势如下:a、遍历数据有序 b、skiplist空间消耗略小一点,哈希表存在链接指针和表空间消耗。c、哈希表扩容有性能损耗。d、哈希表再极端场景下哈希冲突高,效率下降厉害,需要红黑树补足接力。
8. 总结
本篇文章是高阶数据结构的最后一篇文章. 高阶数据结构的学习之路就到此为止.
相关文章:

【高阶数据结构(八)】跳表详解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:高阶数据结构专栏⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习更多数据结构 🔝🔝 高阶数据结构 1. 前言2. 跳表的概…...

用旧安卓手机当 linux 开发机
1. 下载 Termux (快速链接,如果失效或者要下载最新版请去github release 下载 ) 注意手机硬件,我这个是 64 的所以下 64 的 https://github.com/termux/termux-app/releases/download/v0.118.0/termux-app_v0.118.0github-debug_arm64-v8a.apk 2. 弄到…...
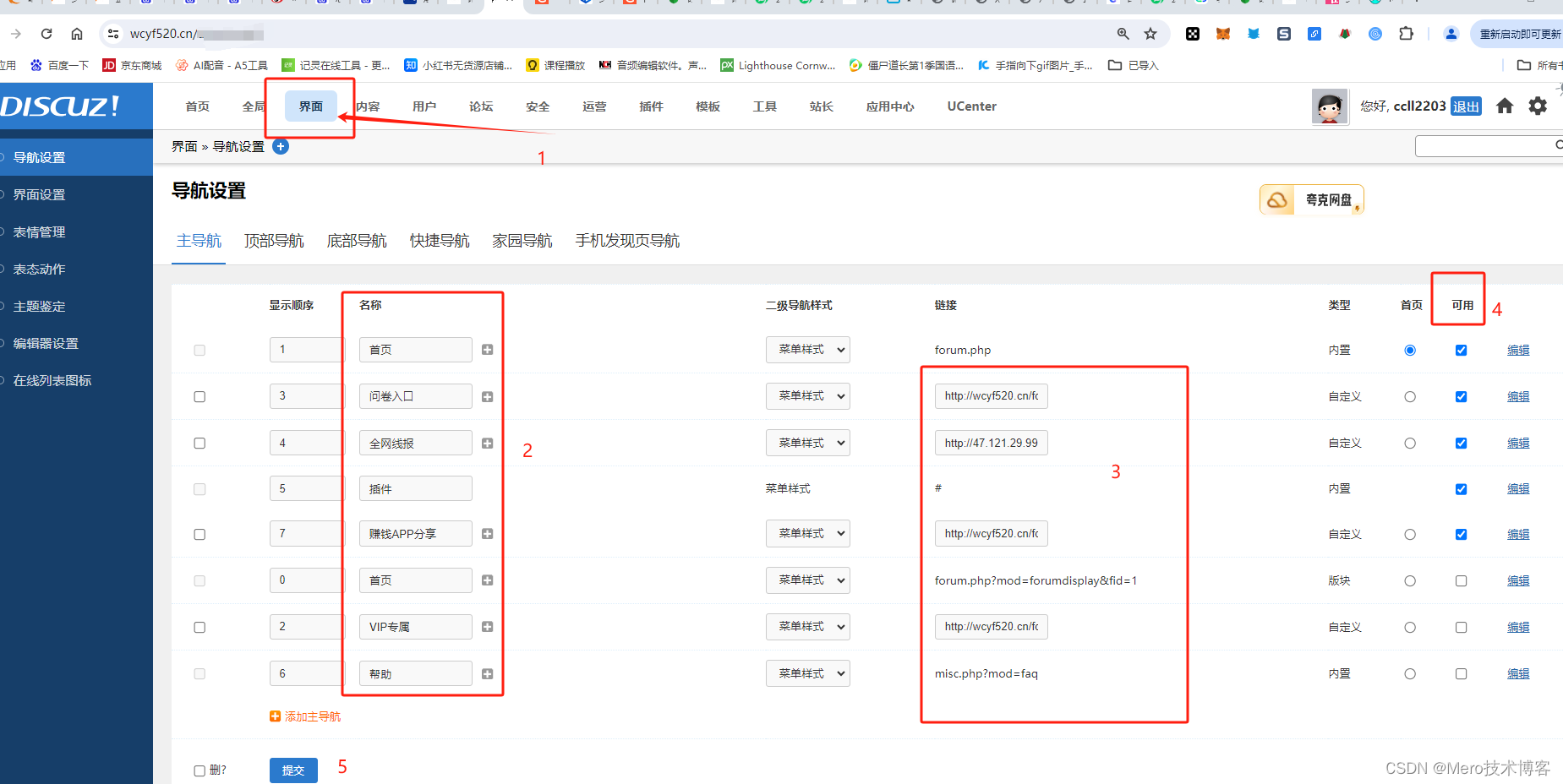
discuz如何添加主导航
大家好,今天教大家怎么样给discuz添加主导航。方法其实很简单,大家跟着我操作既可。一个网站的导航栏是非常重要的,一般用户进入网站的第一印象就是看网站的导航栏。如果大家想看效果的话可以搜索下网创有方,或者直接点击查看效果…...

[每日一练]患某种疾病的患者,正则表达式的匹配
该题目来源于力扣: 1527. 患某种疾病的患者 - 力扣(LeetCode) 题目要求: 患者信息表: Patients ----------------------- | Column Name | Type | ----------------------- | patient_id | int | | pati…...

PHP身份证识别接口、线上平台如何实现身份证实名认证功能?
线上平台实现身份证实名认证的功能,需要结合身份证识别接口来完成。首先,用户通过上传身份证图片或者拍照的方式实现证件信息的提取,身份证实名认证接口通过对提取到的证件信息进行核验,以此来实现线上用户身份的实名认证…...
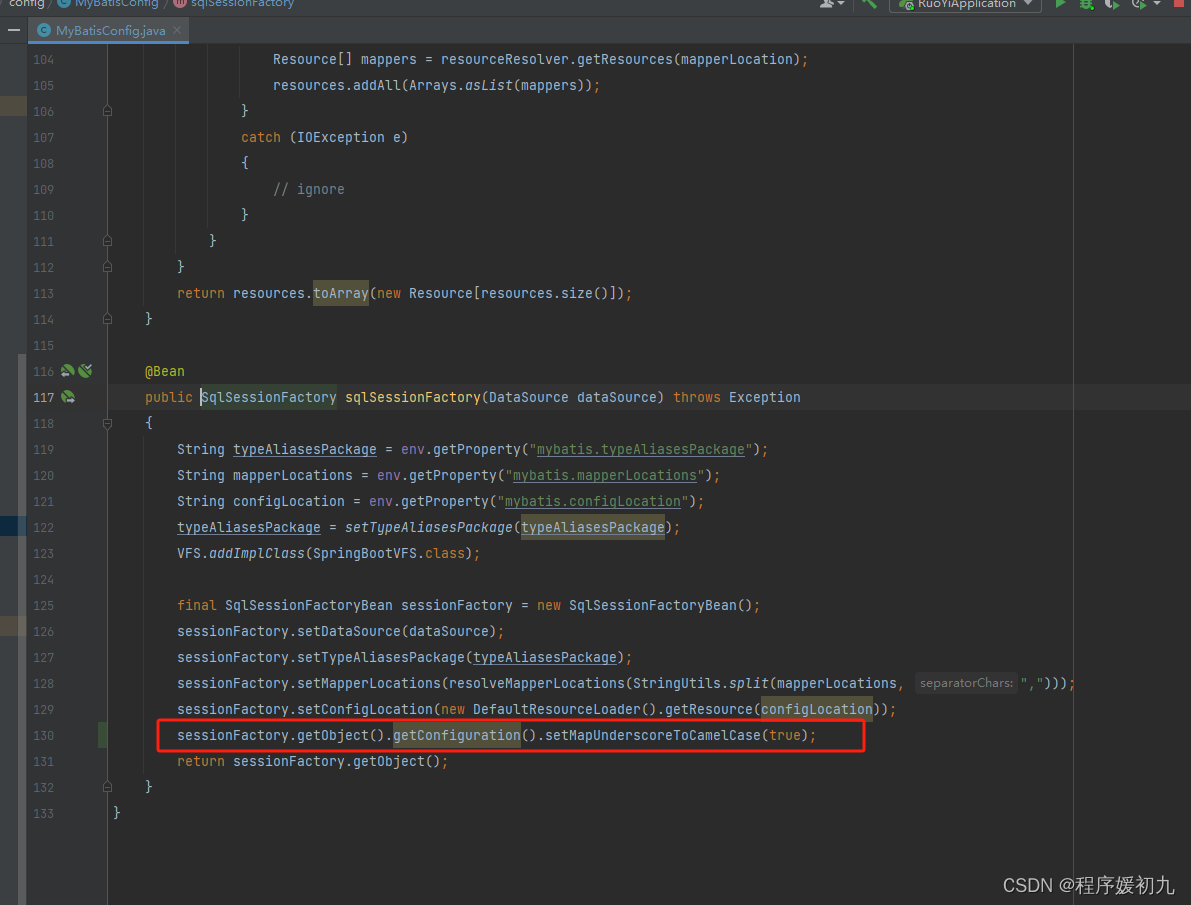
若依:mybatis查询的结果未映射到实体类报null
开启驼峰命名转换: mapUnderscoreToCamelCase: true 我的是mtybatis配置开启驼峰命名转换不生效,还需要在MyBatisConfig中配置 // 配置mybatis自动转驼峰 生效 sessionFactory.getObject().getConfiguration().setMapUnderscoreToCamelCase(true)&#x…...

成都百洲文化传媒有限公司电商服务可信吗?
在当今数字化浪潮席卷之下,电商行业蓬勃发展,成为推动经济增长的重要引擎。在这一领域,成都百洲文化传媒有限公司凭借其专业的电商服务,迅速崛起,成为行业的佼佼者。该公司不仅深谙电商市场的运营之道,更以…...
【递归、搜索与回溯】递归、搜索与回溯准备+递归主题
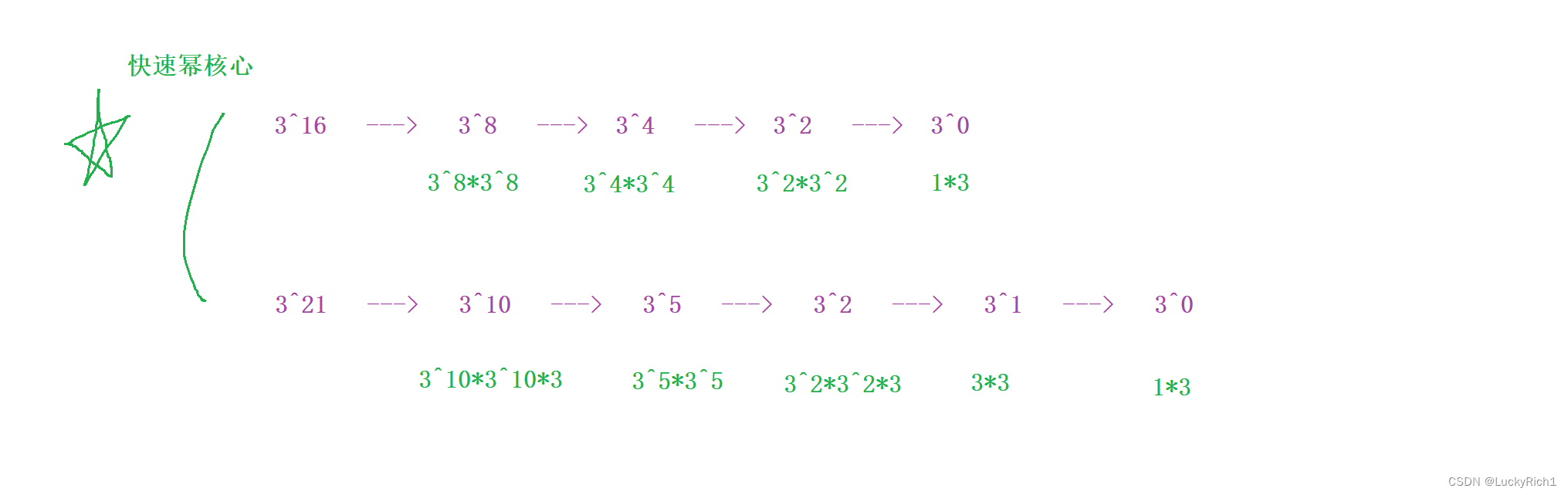
递归、搜索与回溯准备递归主题 1.递归2.搜索3.回溯与剪枝4.汉诺塔问题5.合并两个有序链表6.反转链表7.两两交换链表中的节点8.Pow(x, n)-快速幂(medium) 点赞👍👍收藏🌟🌟关注💖💖 你…...

MVC前端怎么写:深入解析与实战指南
MVC前端怎么写:深入解析与实战指南 在Web开发领域,MVC(Model-View-Controller)是一种广泛使用的架构模式,它将应用程序的数据、界面和控制逻辑分离,使得代码更加清晰、易于维护。本文将详细探讨MVC前端如何…...

LINUX网络设置
一、1.1.ifconfig:当前设备正在启动的网卡(启动的) ifconfig -a :当前所有设备的网卡(启动的和没有启动的都包括) 1.2.ifconfig展示的ens33各行含意: 1.2.1 ens33: flags 4163<UP, …...

双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题: 两数之和II—输入有序数组 给你一个下标从 1 开始的整数数组 numbers ࿰…...
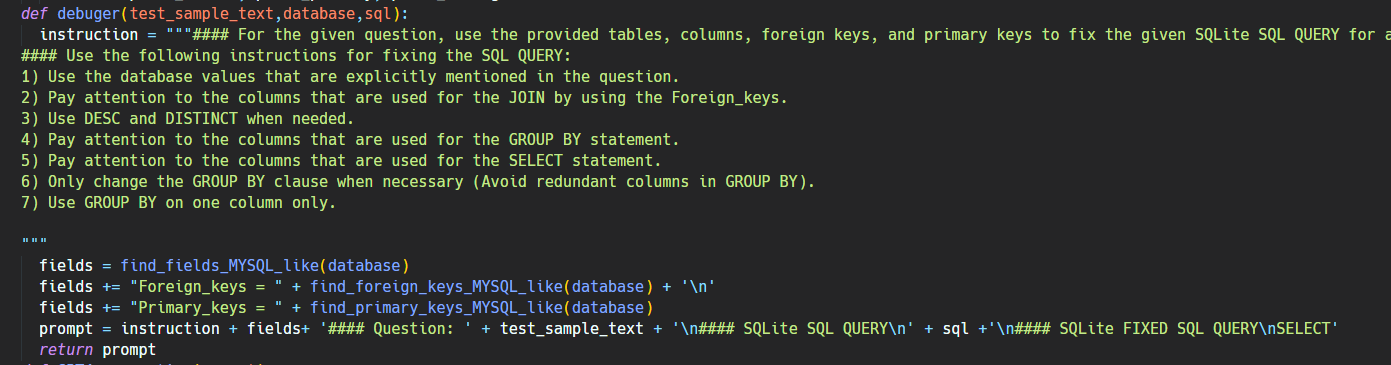
【Text2SQL 论文】DIN-SQL:分解任务 + 自我纠正 + in-context 让 LLM 完成 Text2SQL
论文:DIN-SQL: Decomposed In-Context Learning of Text-to-SQL with Self-Correction ⭐⭐⭐⭐ NeurIPS 2023, arXiv:2304.11015 Code: Few-shot-NL2SQL-with-prompting | GitHub 文章目录 一、论文速读1.1 Schema Linking Module1.2 Classification & Decompo…...

基于Springboot+vue实现的汽车服务管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

ROS2从入门到精通4-3:全局路径规划插件开发案例(以A*算法为例)
目录 0 专栏介绍1 路径规划插件的意义2 全局规划插件编写模板2.1 构造规划插件类2.2 注册并导出插件2.3 编译与使用插件 3 全局规划插件开发案例(A*算法)常见问题 0 专栏介绍 本专栏旨在通过对ROS2的系统学习,掌握ROS2底层基本分布式原理,并具有机器人建…...
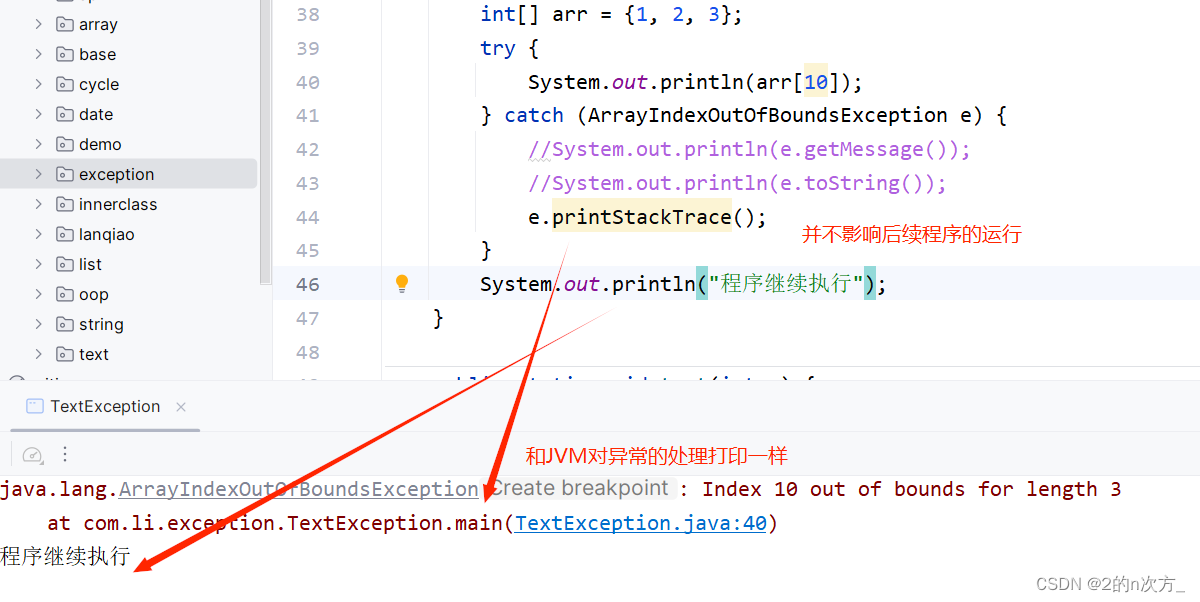
Java学习【认识异常】
Java学习【认识异常】 认识异常异常的种类异常的作用 异常的处理方式JVM默认的处理方式捕获异常finally 多个异常的处理异常中的方法抛出异常 自定义异常 认识异常 在Java中,将程序执行过程中发生的不正常行为称为异常 异常的种类 Error代表的是系统级别的错误&a…...

uniapp+h5 ——微信小程序页面截屏保存在手机
web-view 需要用到 web-view ,类似于iframe, 将网页嵌套到微信小程序中,参数传递等; 示例(无法实时传递数据),页面销毁时才能拿到h5传递的数据,只能利用这点点击跳转到小程序另一个…...
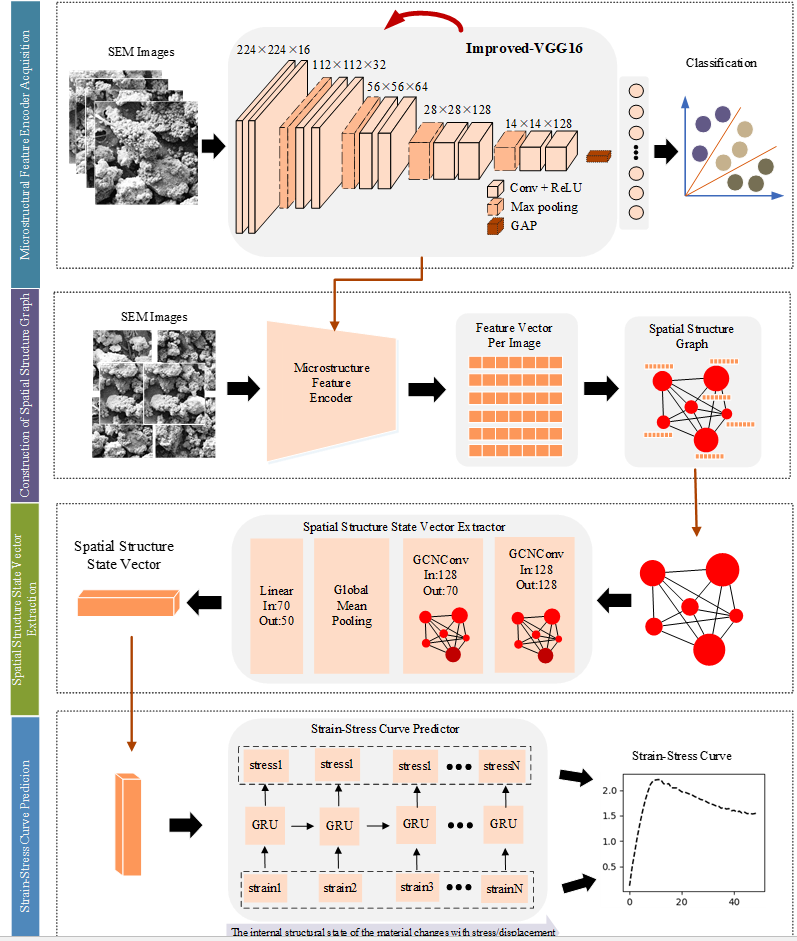
三、基于图像分类预训练编码及图神经网络的预测模型 【框图+源码】
背景: 抽时间补充,先挖个坑。 一、模型结构 二、源码...
Linux - 高级IO
目录 理解五种IO模型非阻塞IO的设置多路转接之select 实现一个简易的select服务器select服务器的优缺点 多路转接之poll 实现一个简易的poll服务器poll服务器的优缺点 多路转接之epoll epoll原理epoll的优势用epoll实现一个简易的echo服务器 epoll的LT和ET工作模式 什么是LT和…...

面试题:说一下 http 报文都有哪些东西?
面试题:说一下 http 报文都有哪些东西? HTTP 是传输超文本(实际上除了 HTML,可以传输任何类型的文件,如视频、音频、文本等)的协议,是一组用于浏览器-服务器之间数据传输的规则。 HTTP 位于 OS…...
开山之作!Python数据与算法分析手册,登顶GitHub!
若把编写代码比作行军打仗,那么要想称霸沙场,不能仅靠手中的利刃,还需深谙兵法。 Python是一把利刃,数据结构与算法则是兵法。只有熟读兵法,才能使利刃所向披靡。只有洞彻数据结构与算法,才能真正精通Pyth…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
