成都百洲文化传媒有限公司电商服务可信吗?
在当今数字化浪潮席卷之下,电商行业蓬勃发展,成为推动经济增长的重要引擎。在这一领域,成都百洲文化传媒有限公司凭借其专业的电商服务,迅速崛起,成为行业的佼佼者。该公司不仅深谙电商市场的运营之道,更以其创新的服务理念和高效的执行力,赢得了广大客户的信赖和好评。
成都百洲文化传媒有限公司自成立之初,便明确了自己的定位——专注于为电商行业提供全方位、专业化的服务。公司拥有一支经验丰富、技术精湛的团队,他们深入了解电商行业的运作机制和发展趋势,能够为客户提供从市场分析、战略规划到运营执行等一站式服务。无论是帮助传统企业转型电商,还是为新兴电商品牌打造个性化营销方案,百洲文化都能凭借其专业的知识和经验,为客户量身定制最适合的解决方案。

在电商服务领域,成都百洲文化传媒有限公司注重创新,不断探索新的服务模式和营销手段。公司紧跟时代潮流,积极运用大数据、人工智能等先进技术,提升服务质量和效率。同时,百洲文化还注重与客户的沟通与合作,深入了解客户的需求和痛点,从而为客户提供更加精准、有效的服务。
除了专业的服务和创新的理念,成都百洲文化传媒有限公司还非常注重品牌建设和市场推广。公司积极参与各类行业活动和展览,展示自己的专业实力和服务成果,不断提升品牌知名度和影响力。同时,百洲文化还通过自媒体平台等渠道,加强与客户和消费者的互动,传递公司的价值理念和服务优势。
正是因为成都百洲文化传媒有限公司在电商服务领域的出色表现,该公司不仅赢得了客户的认可,还获得了行业的广泛赞誉。未来,随着电商行业的持续发展和市场竞争的加剧,百洲文化将继续秉承专业、创新、服务的理念,不断提升自身实力和服务水平,为电商行业的发展贡献更多的力量。
相关文章:

成都百洲文化传媒有限公司电商服务可信吗?
在当今数字化浪潮席卷之下,电商行业蓬勃发展,成为推动经济增长的重要引擎。在这一领域,成都百洲文化传媒有限公司凭借其专业的电商服务,迅速崛起,成为行业的佼佼者。该公司不仅深谙电商市场的运营之道,更以…...
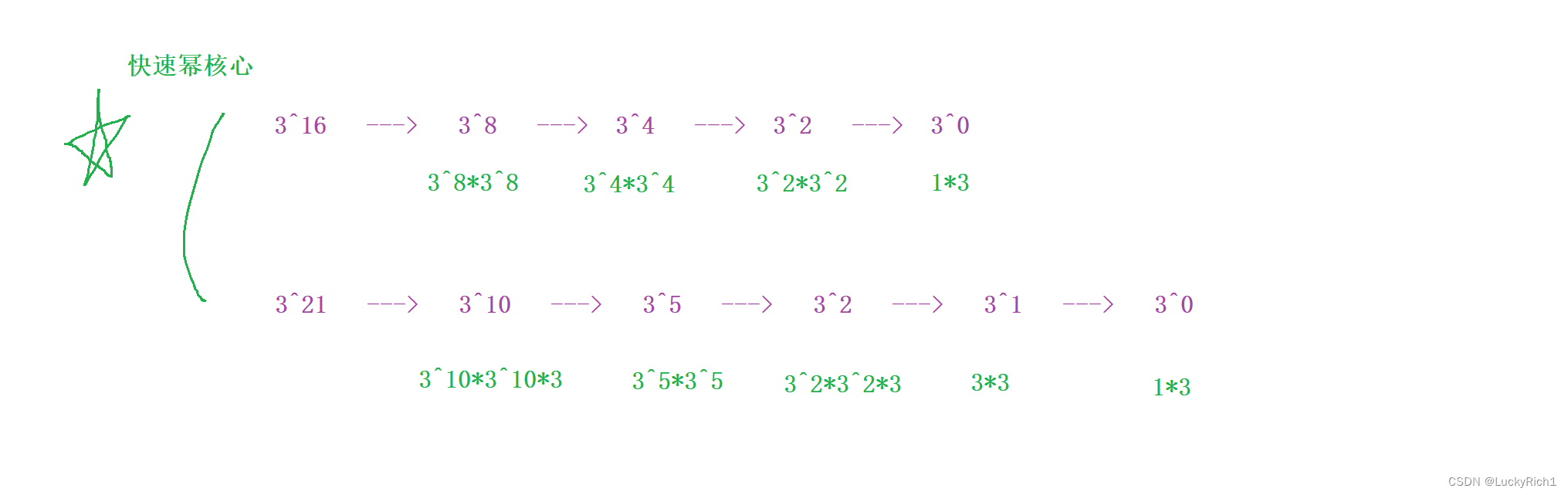
【递归、搜索与回溯】递归、搜索与回溯准备+递归主题
递归、搜索与回溯准备递归主题 1.递归2.搜索3.回溯与剪枝4.汉诺塔问题5.合并两个有序链表6.反转链表7.两两交换链表中的节点8.Pow(x, n)-快速幂(medium) 点赞👍👍收藏🌟🌟关注💖💖 你…...

MVC前端怎么写:深入解析与实战指南
MVC前端怎么写:深入解析与实战指南 在Web开发领域,MVC(Model-View-Controller)是一种广泛使用的架构模式,它将应用程序的数据、界面和控制逻辑分离,使得代码更加清晰、易于维护。本文将详细探讨MVC前端如何…...

LINUX网络设置
一、1.1.ifconfig:当前设备正在启动的网卡(启动的) ifconfig -a :当前所有设备的网卡(启动的和没有启动的都包括) 1.2.ifconfig展示的ens33各行含意: 1.2.1 ens33: flags 4163<UP, …...

双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题: 两数之和II—输入有序数组 给你一个下标从 1 开始的整数数组 numbers ࿰…...
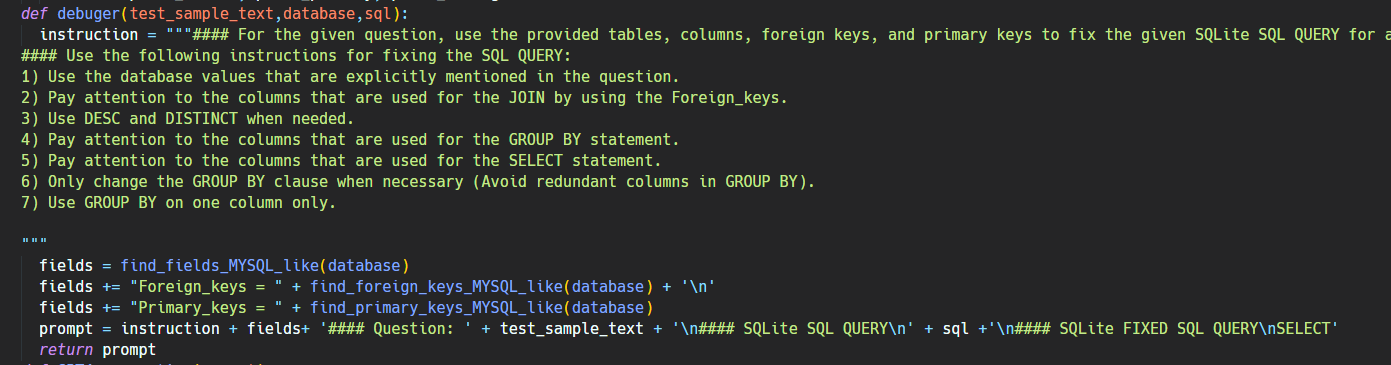
【Text2SQL 论文】DIN-SQL:分解任务 + 自我纠正 + in-context 让 LLM 完成 Text2SQL
论文:DIN-SQL: Decomposed In-Context Learning of Text-to-SQL with Self-Correction ⭐⭐⭐⭐ NeurIPS 2023, arXiv:2304.11015 Code: Few-shot-NL2SQL-with-prompting | GitHub 文章目录 一、论文速读1.1 Schema Linking Module1.2 Classification & Decompo…...

基于Springboot+vue实现的汽车服务管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

ROS2从入门到精通4-3:全局路径规划插件开发案例(以A*算法为例)
目录 0 专栏介绍1 路径规划插件的意义2 全局规划插件编写模板2.1 构造规划插件类2.2 注册并导出插件2.3 编译与使用插件 3 全局规划插件开发案例(A*算法)常见问题 0 专栏介绍 本专栏旨在通过对ROS2的系统学习,掌握ROS2底层基本分布式原理,并具有机器人建…...
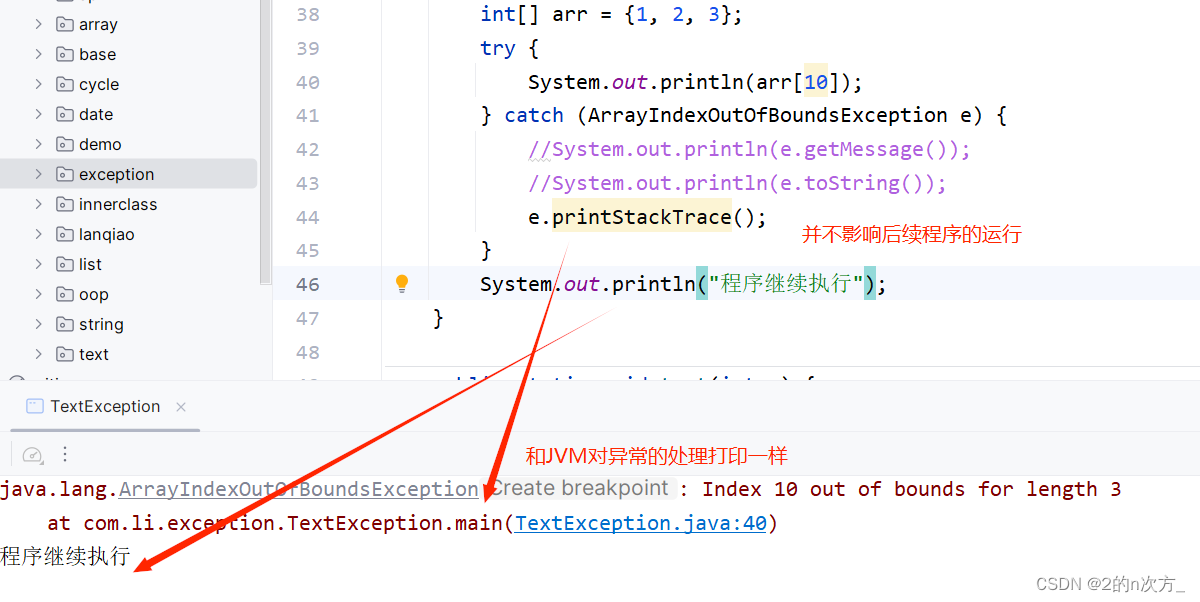
Java学习【认识异常】
Java学习【认识异常】 认识异常异常的种类异常的作用 异常的处理方式JVM默认的处理方式捕获异常finally 多个异常的处理异常中的方法抛出异常 自定义异常 认识异常 在Java中,将程序执行过程中发生的不正常行为称为异常 异常的种类 Error代表的是系统级别的错误&a…...

uniapp+h5 ——微信小程序页面截屏保存在手机
web-view 需要用到 web-view ,类似于iframe, 将网页嵌套到微信小程序中,参数传递等; 示例(无法实时传递数据),页面销毁时才能拿到h5传递的数据,只能利用这点点击跳转到小程序另一个…...
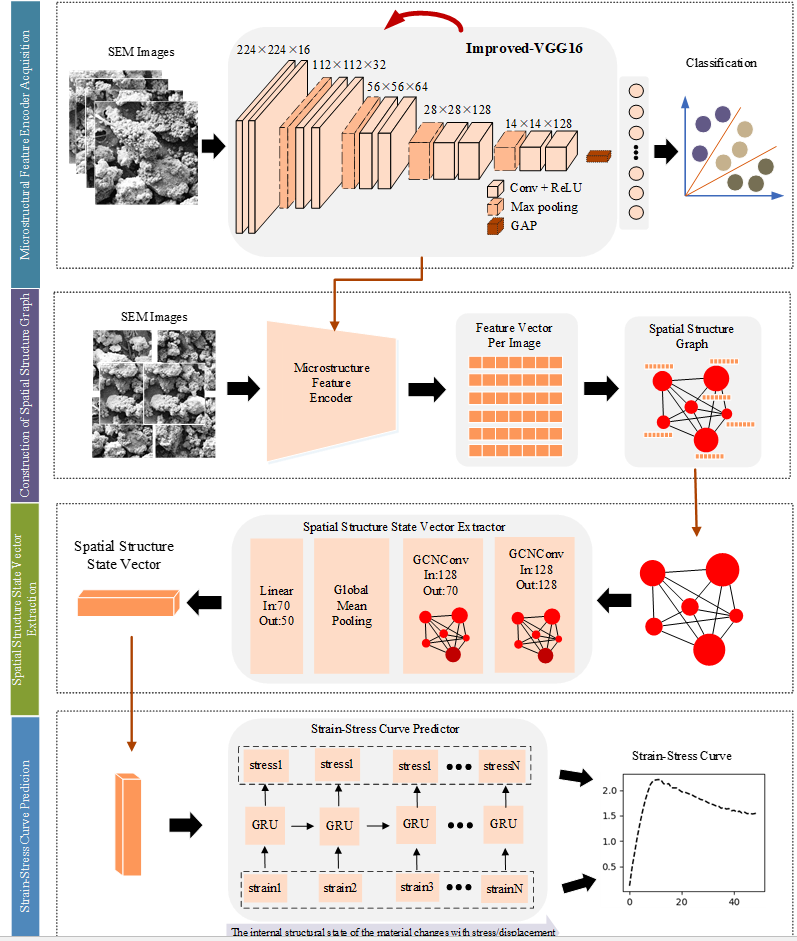
三、基于图像分类预训练编码及图神经网络的预测模型 【框图+源码】
背景: 抽时间补充,先挖个坑。 一、模型结构 二、源码...
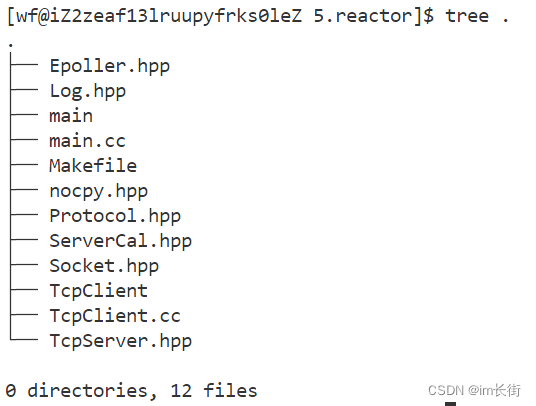
Linux - 高级IO
目录 理解五种IO模型非阻塞IO的设置多路转接之select 实现一个简易的select服务器select服务器的优缺点 多路转接之poll 实现一个简易的poll服务器poll服务器的优缺点 多路转接之epoll epoll原理epoll的优势用epoll实现一个简易的echo服务器 epoll的LT和ET工作模式 什么是LT和…...

面试题:说一下 http 报文都有哪些东西?
面试题:说一下 http 报文都有哪些东西? HTTP 是传输超文本(实际上除了 HTML,可以传输任何类型的文件,如视频、音频、文本等)的协议,是一组用于浏览器-服务器之间数据传输的规则。 HTTP 位于 OS…...
开山之作!Python数据与算法分析手册,登顶GitHub!
若把编写代码比作行军打仗,那么要想称霸沙场,不能仅靠手中的利刃,还需深谙兵法。 Python是一把利刃,数据结构与算法则是兵法。只有熟读兵法,才能使利刃所向披靡。只有洞彻数据结构与算法,才能真正精通Pyth…...

编译安装gcc-11及可能遇到的bug
编译安装脚本 GCC_VERSION11.1.0 PACKAGE_DIR/path/to/gcc/source/code GCC_DIR$PACKAGE_DIR/gcc-$GCC_VERSION GCC_INSTALL_DIR/path/to/install/gccmkdir -p $GCC_INSTALL_DIR cd $GCC_INSTALL_DIR rm -rf * cd $PACKAGE_DIR rm -rf gcc-$GCC_VERSION if [ ! -f "gcc-$…...

vue项目引入json/js文件批量或单个方法
vue项目 json // 方式一 : 将文件内容完整的引入 import json from ./src/assets/xxx.json console.log(json) console.log(---)// 方式二 : 部分引入-名称必须是文件中定义的key import {name1,name2} from ./src/assets/xxx.json console.log(name1)…...
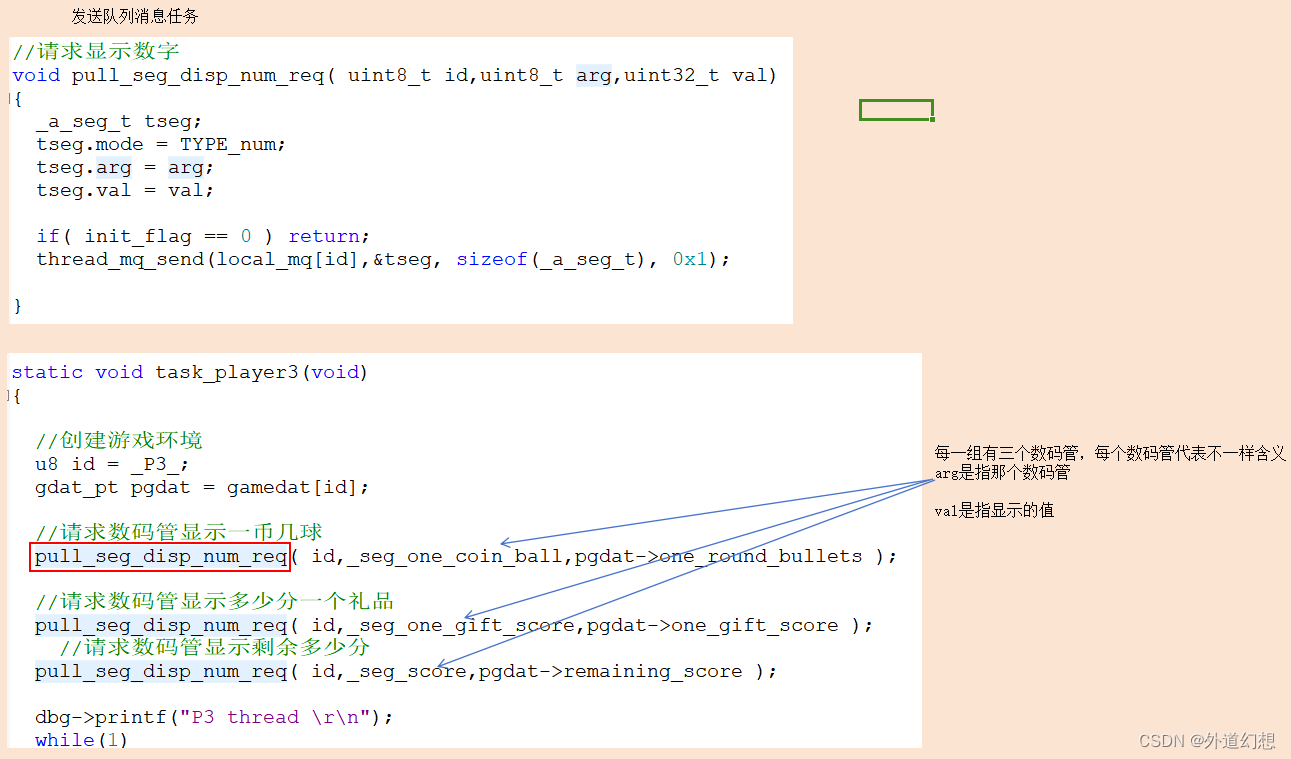
守护任务用来防止资源冲突
背景:有三个任务,他们都需要操作数码管。每个任务对应三个数码管,共9个数码管。硬件上9个数码管的控制使用一套硬件完成。 策略:每个任务都往自己的队列里面发数据,单独建立一个监听任务:处理所有队列的数…...

fast admin实现多数据库导入数据
思路 1创建多数据库连接 2后端的前台代码能使用get或者post请求传递选中数据给后台 3后台能够接收到 4后台接收到id或者全字段数据后对数据进行处理,然后使用多数据库操作将其存入第二个数据库 实现 1config文件下创建新数据库连接 db_config2 > [// 数据库类…...

NLP基础——序列模型(动手学深度学习)
序列模型 定义 序列模型是自然语言处理(NLP)和机器学习领域中一类重要的模型,它们特别适合处理具有时间顺序或序列结构的数据,例如文本、语音信号或时间序列数据。 举个例子:一部电影的评分在不同时间段的评分可能是…...

机器学习AI大模型的开源与闭源:哪个更好?
文章目录 前言一、开源AI模型1.1 开源的优点1.2 开源的缺点 二、闭源AI模型2.1 闭源的优点2.2 闭源的缺点 三、开源与闭源的平衡3.1 开源与闭源结合的案例3.2 开源与闭源的战略选择 小结 前言 在过去的几年里,人工智能(AI)和机器学习…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
