MT2084 检测敌人



思路:
1. 以装置为中心->以敌人为中心。
以敌人为中心,r为半径做圆,与x轴交于a,b点,则在[a,b]之间的装置都能覆盖此敌人。
每个敌人都有[a,b]区间,则此题转化为:有多少个装置能覆盖到这些[a,b]区间。(“覆盖”指的是装置所在的位置在[a,b]线段上)
2.使用贪心:首先将所有线段进行排序(按右端点由小到大),每次将装置放在第一个未覆盖线段的右端点上。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
struct enemy
{double x, y, r, l;bool v;
} e[N];
bool cmp(enemy a, enemy b)
{return a.r < b.r;
}
int main()
{int n;double r;while (cin >> n >> r && !(n == 0 && r == 0)){bool flag = false;memset(e, 0, sizeof e);for (int i = 1; i <= n; i++){cin >> e[i].x >> e[i].y;if (r * r < e[i].y * e[i].y) // 不可覆盖{flag = true;}else{ // 求在x轴上的投影e[i].l = e[i].x - sqrt(r * r - e[i].y * e[i].y);e[i].r = sqrt(r * r - e[i].y * e[i].y) + e[i].x;e[i].v = false;}}if (flag){ // 以敌人为中心,r为半径的圆与x无交点:不可覆盖cout << -1 << endl;continue;}sort(e + 1, e + 1 + n, cmp);int ans = 0;for (int i = 1; i <= n; i++){ // 从小到大检测每一条线段if (e[i].v == false){ // 此敌人还未被检测for (int j = i; j <= n; j++){if (e[j].v == false && e[j].l <= e[i].r) // 未被检测的敌人线段与当前线段有交集{e[j].v = true;}}e[i].v = true;ans++;}}cout << ans << endl;}return 0;
}相关文章:

MT2084 检测敌人
思路: 1. 以装置为中心->以敌人为中心。 以敌人为中心,r为半径做圆,与x轴交于a,b点,则在[a,b]之间的装置都能覆盖此敌人。 每个敌人都有[a,b]区间,则此题转化为:有多少个装置能覆盖到这些[a,b]区间。…...

支持向量机、随机森林、K最近邻和逻辑回归-九五小庞
支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest)、K最近邻(K-Nearest Neighbors, KNN)和逻辑回归(Logistic Regression)是机器学习和统计学习中常用的分类算法。…...

MySQL—多表查询—多表关系介绍
一、引言 提到查询,我们想到之前学习的单表查询(DQL语句)。而这一章节部分的博客我们将要去学习和了解多表查询。 对于多表查询,主要从以下7个方面进行学习。 (1)第一部分:介绍 1、多表关系 2、…...

Vue基础篇--table的封装
1、 在components文件夹中新建一个ITable的vue文件 <template><div class"tl-rl"><template :table"table"><el-tablev-loading"table.loading":show-summary"table.hasShowSummary":summary-method"table…...

mysql中optimizer trace的作用
大家好。对于MySQL 5.6以及之前的版本来说,查询优化器就像是一个黑盒子一样,我们只能通过EXPLAIN语句查看到最后 优化器决定使用的执行计划,却无法知道它为什么做这个决策。于是在MySQL5.6以及之后的版本中,MySQL新增了一个optimi…...

实习面试题(答案自敲)、
1、为什么要重写equals方法,为什么重写了equals方法后,就必须重写hashcode方法,为什么要有hashcode方法,你能介绍一下hashcode方法吗? equals方法默认是比较内存地址;为了实现内容比较,我们需要…...

二叉树讲解
目录 前言 二叉树的遍历 层序遍历 队列的代码 queuepush和queuepushbujia的区别 判断二叉树是否是完全二叉树 前序 中序 后序 功能展示 创建二叉树 初始化 销毁 简易功能介绍 二叉树节点个数 二叉树叶子节点个数 二叉树第k层节点个数 二叉树查找值为x的节点 判…...
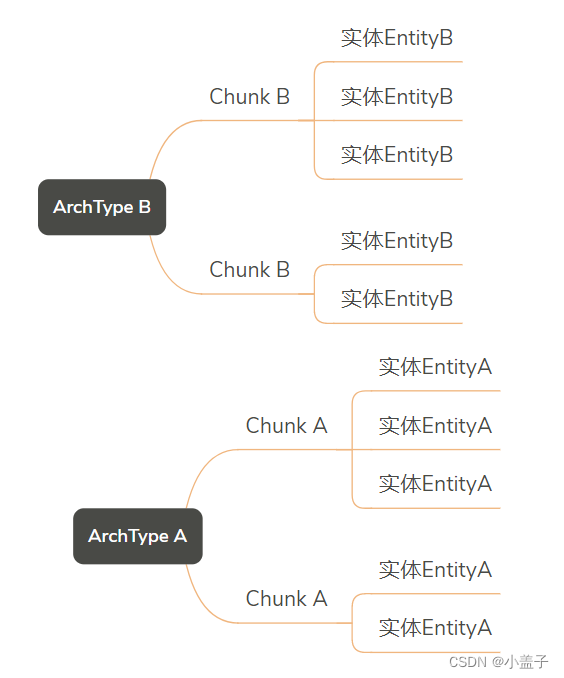
Unity DOTS技术(五)Archetype,Chunk,NativeArray
文章目录 一.Chunk和Archetype什么是Chunk?什么是ArchType 二.Archetype创建1.创建实体2.创建并添加组件3.批量创建 三.多线程数组NativeArray 本次介绍的内容如下: 一.Chunk和Archetype 什么是Chunk? Chunk是一个空间,ECS系统会将相同类型的实体放在Chunk中.当一个Chunk…...

算法学习笔记(7.1)-贪心算法(分数背包问题)
##问题描述 给定 𝑛 个物品,第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ,和一个容量为 𝑐𝑎&…...

气膜建筑的施工对周边环境影响大吗?—轻空间
随着城市化进程的加快,建筑行业的快速发展也带来了环境问题。噪音、灰尘和建筑废料等对周边居民生活和生态环境造成了不小的影响。因此,选择一种环保高效的施工方式变得尤为重要。气膜建筑作为一种新兴的建筑形式,其施工过程对周边环境的影响…...

【计算机网络】对应用层HTTP协议的重点知识的总结
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

30分钟快速入门TCPDump
TCPDump是一款功能强大的网络分析工具,它可以帮助网络管理员捕获并分析流经网络接口的数据包。由于其在命令行环境中的高效性与灵活性,TCPDump成为了网络诊断与安全分析中不可或缺的工具。本文将详细介绍TCPDump的基本用法,并提供一些高级技巧…...

Python | 刷题日记
1.海伦公式求三角形的面积 area根号下(p(p-a)(p-b)(p-c)) p是周长的一半 2.随机生成一个整数 import random xrandom.randint(0,9)#随机生成0到9之间的一个数 yeval(input("please input:")) if xy:print("bingo") elif x<y:pri…...
“JS逆向 | Python爬虫 | 动态cookie如何破~”
案例目标 目标网址:aHR0cHMlM0EvL21hdGNoLnl1YW5yZW54dWUuY29tL21hdGNoLzI= 本题目标:提取全部 5 页发布日热度的值,计算所有值的加和,并提交答案 常规 JavaScript 逆向思路 JavaScript 逆向工程通常分为以下三步: 寻找入口:逆向工程的核心在于找出加密参数的生成方式。…...
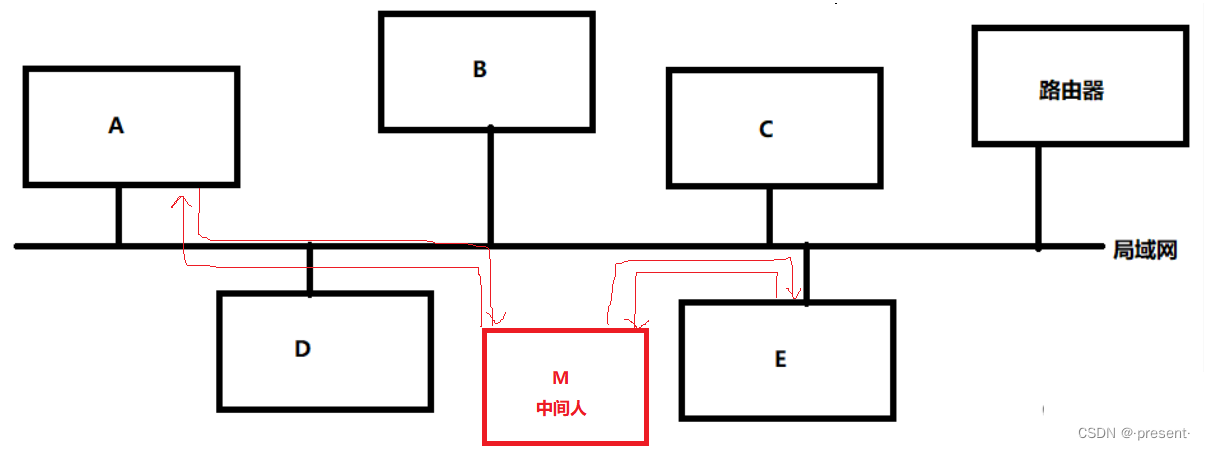
十.数据链路层——MAC/ARP
IP和数据链路层之间的关系 引言 在IP一节中,我们说IP层路由(数据转发)的过程,就像我们跳一跳游戏一样,从一个节点,转发到另一个节点 它提供了一种将数据从A主机跨网络发到B主机的能力 什么叫做跨网络??&a…...

Linux主机安全可视化运维(免费方案)
本文介绍如何使用免费的主机安全软件,在自有机房或企业网络实现对Linux系统进行可视化“主机安全”管理。 一、适用对象 本文适用于个人或企业内的Linux服务器运维场景,实现免费、高效、可视化的主机安全管理。提前发现主机存在的安全风险,全方位实时监控主机运行时入侵事…...

Vite + Vue 3 前端项目实战
一、项目创建 npm install -g create-vite #安装 Vite 项目的脚手架工具 # 或者使用yarn yarn global add create-vite#创建vite项目 create-vite my-vite-project二、常用Vue项目依赖安装 npm install unplugin-auto-import unplugin-vue-components[1] 安装按需自动导入组…...

python-字符替换
[题目描述] 给出一个字符串 s 和 q 次操作,每次操作将 s 中的某一个字符a全部替换成字符b,输出 q 次操作后的字符串输入 输入共 q2 行 第一行一个字符串 s 第二行一个正整数 q,表示操作次数 之后 q 行每行“a b”表示把 s 中所有的a替换成b输…...
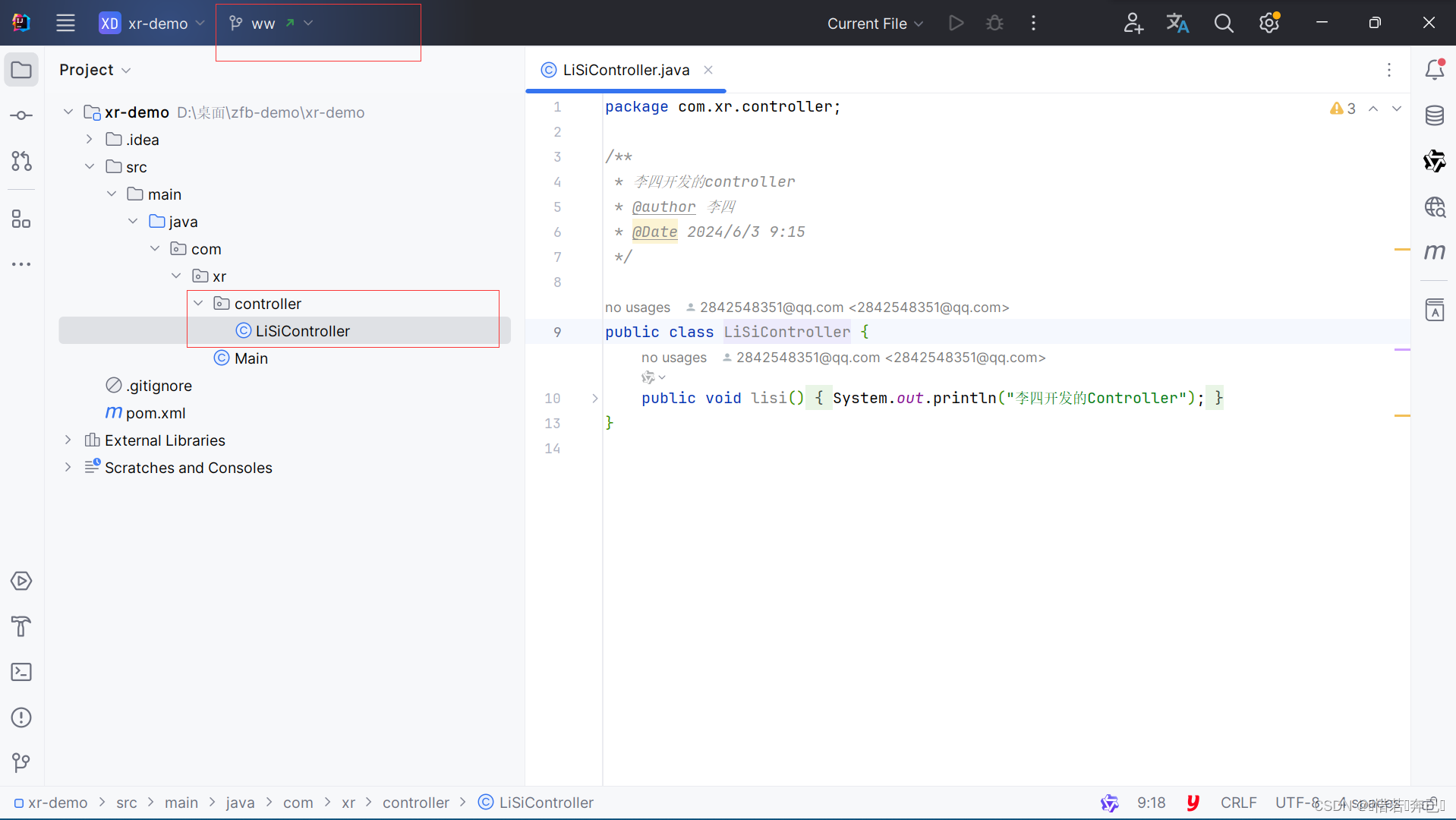
团队项目开发使用git工作流(IDEA)【精细】
目录 开发项目总体使用git流程 图解流程 1.创建项目仓库[组长完成] 2. 创建项目,并进行绑定远程仓库【组长完成】 3.将项目与远程仓库(gitee)进行绑定 3.1 创建本地的git仓库 3.2 将项目添加到缓存区 3.3 将项目提交到本地仓库&#…...

爬虫案例实战
文章目录 一、窗口切换实战二、京东数据抓取 一、窗口切换实战 案例实战:使用selenium实现打开百度和腾讯两个窗口并切换 知识点:用到selenium中execute_script()执行js代码及switch_to.window()方法 全部代码如下: import time import war…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
