这个高考作文满分的极客,想和你聊聊新媒体写作

计育韬
曾为上海市高考作文满分考生
微信官方 SVG AttributeName 开发者
新榜 500 强运营人
复旦大学青年智库讲师
浙江传媒学院客座导师
上海团市委新媒体顾问
上海市金山区青联副主席
文案能力,从来就不是一蹴而就的。今天,来和大家聊聊当年我的高考作文为什么满分,以及从中有哪些可以在新媒体写作中借鉴的写作习惯。文章比较干,但相信能给予你收获。
我所要谈得并不是当年那篇作文我是“怎么写的”,而是“怎么准备的”。就好比现在的数字营销文案设计一样,好文本的选题、措辞、行文、逻辑是准备出来的。所以当年的考题和我的作文内容最后再谈。
我的高考是比较幸运的,作文的满分是我能踏入复旦的重要原因之一。就在高考完不久,我收到了市教委寄来的范文集和稿费。评分为一类卷上,位列第七篇,得分满分。
文案高手必备思维导图
我在高中的时候就习惯使用思维导图软件,高考前的一周我则回归纸笔,在一张普通A4大小的纸张上完成了「高考作文万能思维导图」。
首先,是选题池。挑选任意一家官方媒体门户网站(这里的官方是指人民网这类),按照其顶部新闻分类,将人世百态分割为若干领域。你可能觉得这些网站无聊,但这些网站的新闻分类绝对是最专业的。
接下来,开始丰富每个领域的论据,构建不同领域之间的相关性。在职场写广告、媒体、公关文案也是一样的。整个行业的方方面面,要在脑海中建议构造逻辑关系,没有全局观的文案写不出好作品。
构建说服力
其次,是论据。仅从高考角度来说,我不选古代论据 1.家喻户晓的前辈早已烂大街 2.别出心裁的案例如果阅卷老师也不太清楚,即使这个论据再高大上老师也不敢给非常高的分数。
更重要的是,文案要给当代以考量,给未来以预判。比如新媒体写作中,传播广泛的文章一定针砭时弊,或昭示未来。
何况由于我的选课是政治,我也一向是拒绝写高中式议论文,而是写「时评」。真正好文章的说服力在于唤醒用户的认同,而不是用自己的逻辑和陈旧的论据强行支撑某个观点。
洞察读者需求
高考作文是给阅卷老师看的,新媒体文案是给特定受众看的。同一个议题,完全可以有不同的行文办法。懂得用户体验是文案写作的重中之重。
1.高中式「议论文」其实是高中老师假想并强加于高中生的思维模式。实际上,大学生和职场人回头看高中的「议论文」,不得不承认大多数近乎弱智(但高中时的大家其实并没有这么弱智,否则怎么大一就写得出大学论文啦?),这类文体完全不符合成年人的阅读习惯(你在数据库里,哪怕在长微博上会看到高中「议论文」式的文章吗?)时评则是思辨更成熟,也更符合阅卷老师实际生活阅读习惯的行文风格。在一堆议论文中突然出现一篇富有成熟气息的时评,我想大多数阅卷老师在阅读时是更轻松的。
2.对当下社会更有洞察力的考生,阅卷老师自然愿意让 TA 去更好学府就读,因为 TA 的潜在社会贡献力会更大。
3.阅卷组为什么要给出高分?高分作文在评分机制上比较特殊。那时候在上海,我记得一份高考作文常规需要3个阅卷老师批阅,平均分如果过高会落到核心的阅卷组被终审。满分或逼近满分的作文不仅仅是为了把一个考生送到更优秀的学府,而是在于——
将该文作为范文,体现当代高中生积极向上的精神面貌和社会责任意识;与其他省市满分作文比拼,看谁更体现当代高中生精神面貌和社会责任意识;对下一届考生和社会起到积极的影响力,尤其符合社会主义核心价值观,符合当时的国家意识形态。
综上所述,当年我是个心机婊。
所以职场的文案写作也是一样的。写日记你可以由着性子写,但工作要交付的文本请仔细揣摩好阅读者的心态。他是什么职位?什么身份?什么情景下阅读的?
关于思维导图的设计要点
最后,回到论据准备的工作中。将你日常就有深刻见解的事件作为论据,写到思维导图的对应位置去,并附上各类可信度较高的社会专业人士评论;接下来,在不同领域论据之间寻找共性连接,并注明连接关系;最后开始随意自行命题,你可以用以前的高考作文题也可以自己设计,快速在脑海中拟出作文结构,根据每次模拟的情况不断完善你的思维导图。
▼附作文▼

▼市教委解析▼

- END -
相关文章:

这个高考作文满分的极客,想和你聊聊新媒体写作
计育韬 曾为上海市高考作文满分考生 微信官方 SVG AttributeName 开发者 新榜 500 强运营人 复旦大学青年智库讲师 浙江传媒学院客座导师 上海团市委新媒体顾问 上海市金山区青联副主席 文案能力,从来就不是一蹴而就的。今天,来和大家聊聊当年我的…...
:2024.05.25-2024.05.31)
AI推介-多模态视觉语言模型VLMs论文速览(arXiv方向):2024.05.25-2024.05.31
文章目录~ 1.Empowering Visual Creativity: A Vision-Language Assistant to Image Editing Recommendations2.Bootstrap3D: Improving 3D Content Creation with Synthetic Data3.Video-MME: The First-Ever Comprehensive Evaluation Benchmark of Multi-modal L…...

如何通过Python SMTP配置示例发附件邮件?
Python SMTP配置的步骤?SMTP服务器的优缺点有哪些? 当我们需要发送包含附件的邮件时,自动化的解决方案显得尤为重要。Python提供了SMTP库,使我们能够轻松配置并发送带有附件的邮件。AokSend将通过一个示例来展示如何操作…...

amd64
MD64,或"x64",是一种64位元的电脑处理器架构。它是基于现有32位元的x86架构,由AMD公司所开发,应用AMD64指令集的自家产品有Athlon(速龙) 64、Athlon 64 FX、Athlon 64 X2、Turion(炫龙) 64、Opteron(皓龙)、Sempron(闪龙…...
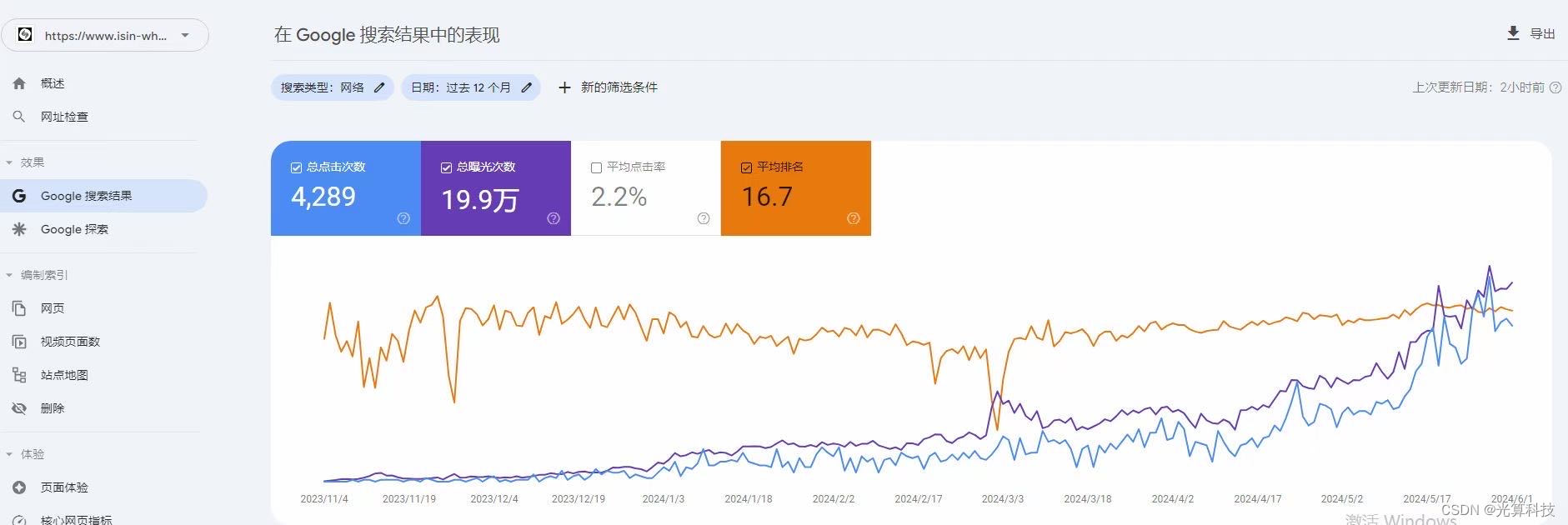
2024如何优化SEO?
在2024年的今天,要问我会如何优化seo,我会专注于几个关键的方面。首先,随着AI内容生成技术的发展,我会利用这些工具来帮助创建或优化我的网站内容,但是,随着谷歌3月份的算法更新,纯粹的ai内容可…...

【NoSQL数据库】Redis命令、持久化、主从复制
Redis命令、持久化、主从复制 redis配置 Redis命令、持久化、主从复制Redis数据类型redis数据库常用命令redis多数据库常用命令1、多数据库间切换2、多数据库间移动数据3、清除数据库内数据 key命令1、keys 命令2、判断键值是否存在exists3、删除当前数据库的指定key del4、获取…...

使用Django JWT实现身份验证
文章目录 安装依赖配置Django设置创建API生成和验证Token总结与展望 在现代Web应用程序中,安全性和身份验证是至关重要的。JSON Web Token(JWT)是一种流行的身份验证方法,它允许在客户端和服务器之间安全地传输信息。Django是一个…...

MT2084 检测敌人
思路: 1. 以装置为中心->以敌人为中心。 以敌人为中心,r为半径做圆,与x轴交于a,b点,则在[a,b]之间的装置都能覆盖此敌人。 每个敌人都有[a,b]区间,则此题转化为:有多少个装置能覆盖到这些[a,b]区间。…...

支持向量机、随机森林、K最近邻和逻辑回归-九五小庞
支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest)、K最近邻(K-Nearest Neighbors, KNN)和逻辑回归(Logistic Regression)是机器学习和统计学习中常用的分类算法。…...

MySQL—多表查询—多表关系介绍
一、引言 提到查询,我们想到之前学习的单表查询(DQL语句)。而这一章节部分的博客我们将要去学习和了解多表查询。 对于多表查询,主要从以下7个方面进行学习。 (1)第一部分:介绍 1、多表关系 2、…...

Vue基础篇--table的封装
1、 在components文件夹中新建一个ITable的vue文件 <template><div class"tl-rl"><template :table"table"><el-tablev-loading"table.loading":show-summary"table.hasShowSummary":summary-method"table…...

mysql中optimizer trace的作用
大家好。对于MySQL 5.6以及之前的版本来说,查询优化器就像是一个黑盒子一样,我们只能通过EXPLAIN语句查看到最后 优化器决定使用的执行计划,却无法知道它为什么做这个决策。于是在MySQL5.6以及之后的版本中,MySQL新增了一个optimi…...

实习面试题(答案自敲)、
1、为什么要重写equals方法,为什么重写了equals方法后,就必须重写hashcode方法,为什么要有hashcode方法,你能介绍一下hashcode方法吗? equals方法默认是比较内存地址;为了实现内容比较,我们需要…...

二叉树讲解
目录 前言 二叉树的遍历 层序遍历 队列的代码 queuepush和queuepushbujia的区别 判断二叉树是否是完全二叉树 前序 中序 后序 功能展示 创建二叉树 初始化 销毁 简易功能介绍 二叉树节点个数 二叉树叶子节点个数 二叉树第k层节点个数 二叉树查找值为x的节点 判…...
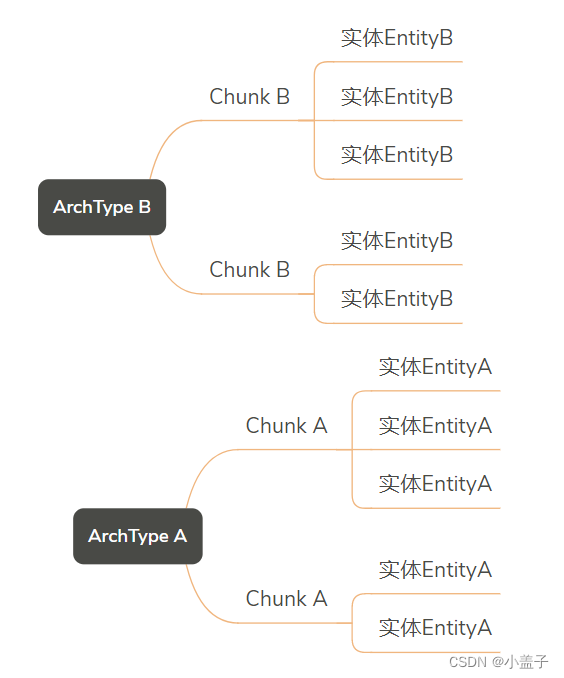
Unity DOTS技术(五)Archetype,Chunk,NativeArray
文章目录 一.Chunk和Archetype什么是Chunk?什么是ArchType 二.Archetype创建1.创建实体2.创建并添加组件3.批量创建 三.多线程数组NativeArray 本次介绍的内容如下: 一.Chunk和Archetype 什么是Chunk? Chunk是一个空间,ECS系统会将相同类型的实体放在Chunk中.当一个Chunk…...

算法学习笔记(7.1)-贪心算法(分数背包问题)
##问题描述 给定 𝑛 个物品,第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ,和一个容量为 𝑐𝑎&…...

气膜建筑的施工对周边环境影响大吗?—轻空间
随着城市化进程的加快,建筑行业的快速发展也带来了环境问题。噪音、灰尘和建筑废料等对周边居民生活和生态环境造成了不小的影响。因此,选择一种环保高效的施工方式变得尤为重要。气膜建筑作为一种新兴的建筑形式,其施工过程对周边环境的影响…...

【计算机网络】对应用层HTTP协议的重点知识的总结
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

30分钟快速入门TCPDump
TCPDump是一款功能强大的网络分析工具,它可以帮助网络管理员捕获并分析流经网络接口的数据包。由于其在命令行环境中的高效性与灵活性,TCPDump成为了网络诊断与安全分析中不可或缺的工具。本文将详细介绍TCPDump的基本用法,并提供一些高级技巧…...

Python | 刷题日记
1.海伦公式求三角形的面积 area根号下(p(p-a)(p-b)(p-c)) p是周长的一半 2.随机生成一个整数 import random xrandom.randint(0,9)#随机生成0到9之间的一个数 yeval(input("please input:")) if xy:print("bingo") elif x<y:pri…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
