如何通过Python SMTP配置示例发附件邮件?
Python SMTP配置的步骤?SMTP服务器的优缺点有哪些?
当我们需要发送包含附件的邮件时,自动化的解决方案显得尤为重要。Python提供了SMTP库,使我们能够轻松配置并发送带有附件的邮件。AokSend将通过一个示例来展示如何操作,并在过程中提及AokSend邮件API的优点。
- Python SMTP:配置基础
要使用Python的SMTP库发送邮件,首先需要进行一些基础配置。这包括设置SMTP服务器地址、端口、发送者邮箱地址、密码以及接收者邮箱地址等。通过正确的配置,我们可以确保邮件能够准确地发送到目标邮箱。
- Python SMTP:添加附件
在配置好SMTP后,下一步是向邮件中添加附件。Python的email模块提供了处理MIME类型的功能。通过创建适当的MIME类型对象,我们可以将文件作为附件添加到邮件中。
- Python SMTP:API优点
- 易用性:提供了简洁明了的API文档和示例代码,使开发者能够快速上手。
- 可靠性:拥有稳定的服务器和强大的邮件处理能力,确保邮件能够高效送达。
- 安全性:支持TLS/SSL加密传输,保护邮件内容的安全。
- 灵活性:提供了丰富的API接口和参数配置选项,满足不同场景下的需求。
- 集成性:可以轻松与其他系统和工具集成,实现自动化的邮件发送和管理。
- Python SMTP:使用工具
当需要处理大量邮件、需要更高级的功能或与其他系统集成时,结合使用AokSend邮件API可能会更加合适。通过将Python SMTP库与AokSend API结合使用,我们可以充分利用两者的优势,实现更高效、更可靠的邮件发送和管理。
在配置和使用Python SMTP库时,请确保遵循最佳实践和安全准则,以确保邮件的顺利发送和接收。AokSend:API/SMTP接口一体化,Python轻松配置,邮件营销高效,品牌传播利器!
相关文章:

如何通过Python SMTP配置示例发附件邮件?
Python SMTP配置的步骤?SMTP服务器的优缺点有哪些? 当我们需要发送包含附件的邮件时,自动化的解决方案显得尤为重要。Python提供了SMTP库,使我们能够轻松配置并发送带有附件的邮件。AokSend将通过一个示例来展示如何操作…...

amd64
MD64,或"x64",是一种64位元的电脑处理器架构。它是基于现有32位元的x86架构,由AMD公司所开发,应用AMD64指令集的自家产品有Athlon(速龙) 64、Athlon 64 FX、Athlon 64 X2、Turion(炫龙) 64、Opteron(皓龙)、Sempron(闪龙…...
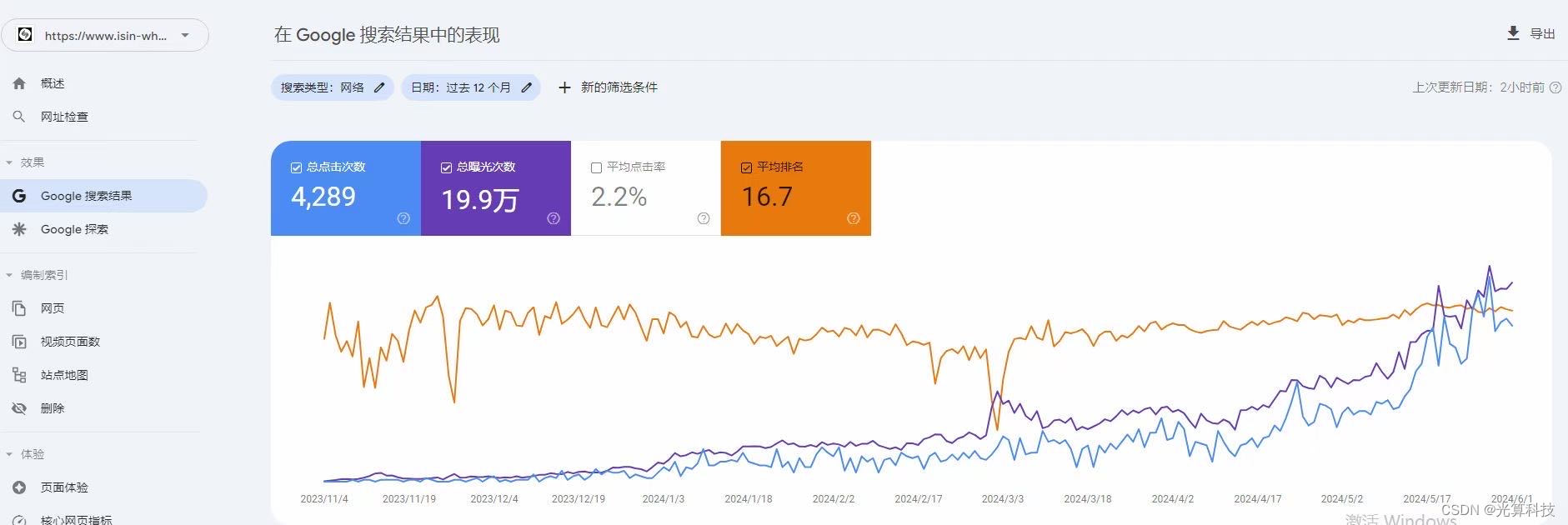
2024如何优化SEO?
在2024年的今天,要问我会如何优化seo,我会专注于几个关键的方面。首先,随着AI内容生成技术的发展,我会利用这些工具来帮助创建或优化我的网站内容,但是,随着谷歌3月份的算法更新,纯粹的ai内容可…...

【NoSQL数据库】Redis命令、持久化、主从复制
Redis命令、持久化、主从复制 redis配置 Redis命令、持久化、主从复制Redis数据类型redis数据库常用命令redis多数据库常用命令1、多数据库间切换2、多数据库间移动数据3、清除数据库内数据 key命令1、keys 命令2、判断键值是否存在exists3、删除当前数据库的指定key del4、获取…...

使用Django JWT实现身份验证
文章目录 安装依赖配置Django设置创建API生成和验证Token总结与展望 在现代Web应用程序中,安全性和身份验证是至关重要的。JSON Web Token(JWT)是一种流行的身份验证方法,它允许在客户端和服务器之间安全地传输信息。Django是一个…...

MT2084 检测敌人
思路: 1. 以装置为中心->以敌人为中心。 以敌人为中心,r为半径做圆,与x轴交于a,b点,则在[a,b]之间的装置都能覆盖此敌人。 每个敌人都有[a,b]区间,则此题转化为:有多少个装置能覆盖到这些[a,b]区间。…...

支持向量机、随机森林、K最近邻和逻辑回归-九五小庞
支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest)、K最近邻(K-Nearest Neighbors, KNN)和逻辑回归(Logistic Regression)是机器学习和统计学习中常用的分类算法。…...

MySQL—多表查询—多表关系介绍
一、引言 提到查询,我们想到之前学习的单表查询(DQL语句)。而这一章节部分的博客我们将要去学习和了解多表查询。 对于多表查询,主要从以下7个方面进行学习。 (1)第一部分:介绍 1、多表关系 2、…...

Vue基础篇--table的封装
1、 在components文件夹中新建一个ITable的vue文件 <template><div class"tl-rl"><template :table"table"><el-tablev-loading"table.loading":show-summary"table.hasShowSummary":summary-method"table…...

mysql中optimizer trace的作用
大家好。对于MySQL 5.6以及之前的版本来说,查询优化器就像是一个黑盒子一样,我们只能通过EXPLAIN语句查看到最后 优化器决定使用的执行计划,却无法知道它为什么做这个决策。于是在MySQL5.6以及之后的版本中,MySQL新增了一个optimi…...

实习面试题(答案自敲)、
1、为什么要重写equals方法,为什么重写了equals方法后,就必须重写hashcode方法,为什么要有hashcode方法,你能介绍一下hashcode方法吗? equals方法默认是比较内存地址;为了实现内容比较,我们需要…...

二叉树讲解
目录 前言 二叉树的遍历 层序遍历 队列的代码 queuepush和queuepushbujia的区别 判断二叉树是否是完全二叉树 前序 中序 后序 功能展示 创建二叉树 初始化 销毁 简易功能介绍 二叉树节点个数 二叉树叶子节点个数 二叉树第k层节点个数 二叉树查找值为x的节点 判…...
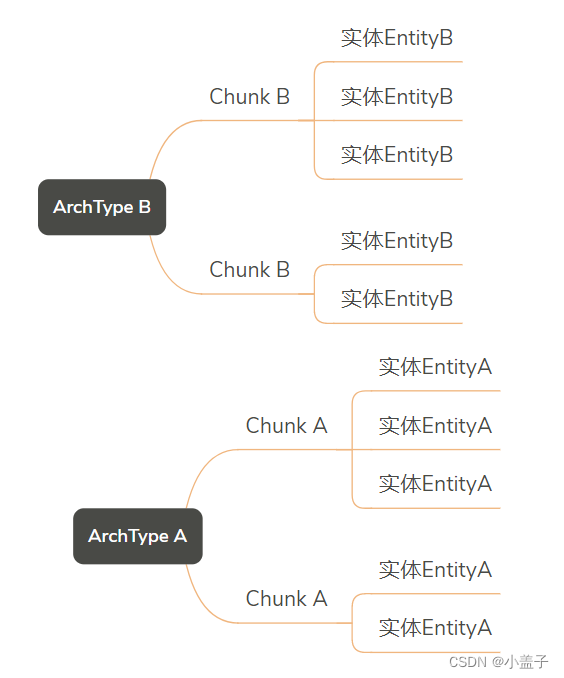
Unity DOTS技术(五)Archetype,Chunk,NativeArray
文章目录 一.Chunk和Archetype什么是Chunk?什么是ArchType 二.Archetype创建1.创建实体2.创建并添加组件3.批量创建 三.多线程数组NativeArray 本次介绍的内容如下: 一.Chunk和Archetype 什么是Chunk? Chunk是一个空间,ECS系统会将相同类型的实体放在Chunk中.当一个Chunk…...

算法学习笔记(7.1)-贪心算法(分数背包问题)
##问题描述 给定 𝑛 个物品,第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ,和一个容量为 𝑐𝑎&…...

气膜建筑的施工对周边环境影响大吗?—轻空间
随着城市化进程的加快,建筑行业的快速发展也带来了环境问题。噪音、灰尘和建筑废料等对周边居民生活和生态环境造成了不小的影响。因此,选择一种环保高效的施工方式变得尤为重要。气膜建筑作为一种新兴的建筑形式,其施工过程对周边环境的影响…...

【计算机网络】对应用层HTTP协议的重点知识的总结
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

30分钟快速入门TCPDump
TCPDump是一款功能强大的网络分析工具,它可以帮助网络管理员捕获并分析流经网络接口的数据包。由于其在命令行环境中的高效性与灵活性,TCPDump成为了网络诊断与安全分析中不可或缺的工具。本文将详细介绍TCPDump的基本用法,并提供一些高级技巧…...

Python | 刷题日记
1.海伦公式求三角形的面积 area根号下(p(p-a)(p-b)(p-c)) p是周长的一半 2.随机生成一个整数 import random xrandom.randint(0,9)#随机生成0到9之间的一个数 yeval(input("please input:")) if xy:print("bingo") elif x<y:pri…...
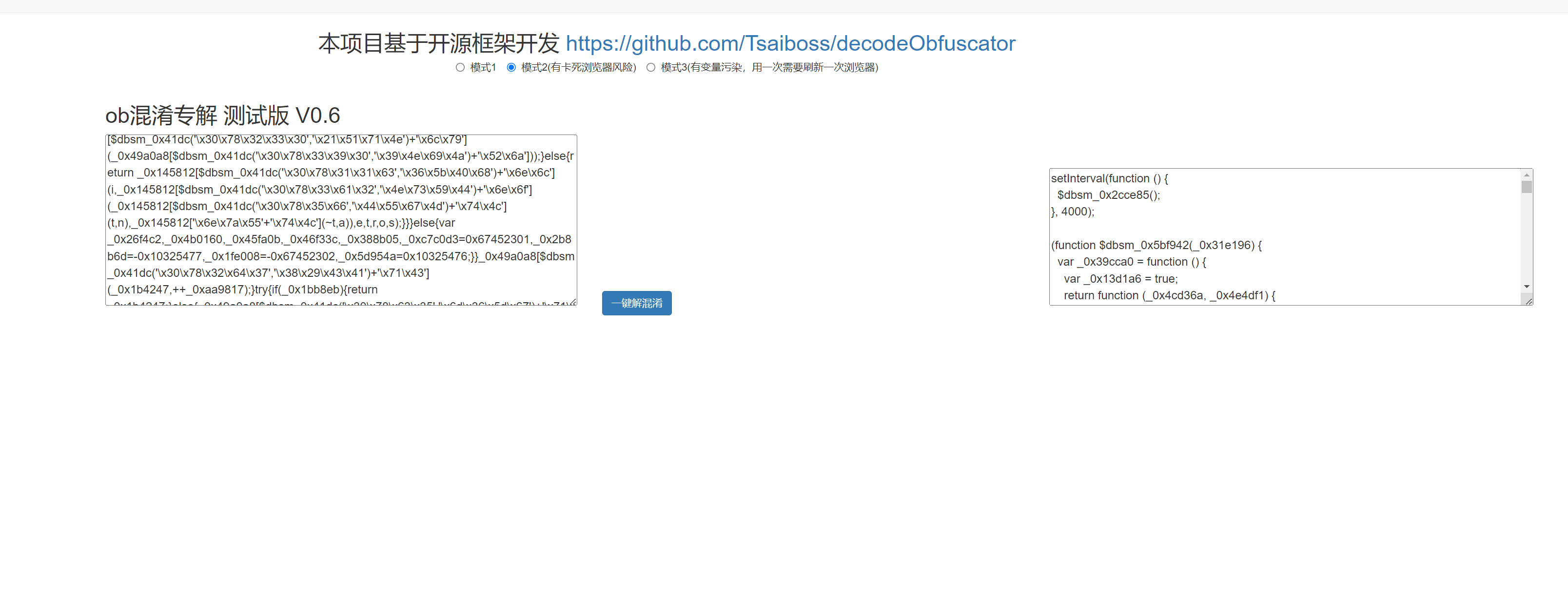
“JS逆向 | Python爬虫 | 动态cookie如何破~”
案例目标 目标网址:aHR0cHMlM0EvL21hdGNoLnl1YW5yZW54dWUuY29tL21hdGNoLzI= 本题目标:提取全部 5 页发布日热度的值,计算所有值的加和,并提交答案 常规 JavaScript 逆向思路 JavaScript 逆向工程通常分为以下三步: 寻找入口:逆向工程的核心在于找出加密参数的生成方式。…...
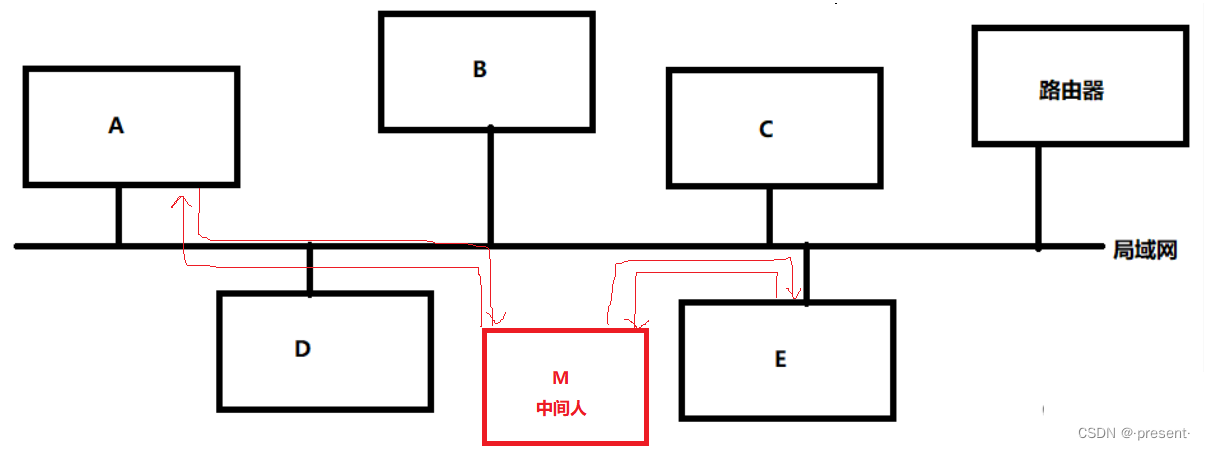
十.数据链路层——MAC/ARP
IP和数据链路层之间的关系 引言 在IP一节中,我们说IP层路由(数据转发)的过程,就像我们跳一跳游戏一样,从一个节点,转发到另一个节点 它提供了一种将数据从A主机跨网络发到B主机的能力 什么叫做跨网络??&a…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
