Java面试题:解决Redis缓存击穿问题
缓存击穿
当一个key过期时,需要对这个key进行数据重建
在重建的时间内如果有大量的并发请求进入,就会绕过缓存进入数据库,会瞬间击垮DB
重建时间可能因为数据是多个表的混合结果需要分头统计而延长,从而更容易出现缓存击穿问题
缓存击穿的解决方案
添加互斥锁
先查询缓存,如果未命中就尝试获取互斥锁,如果成功
查询数据库进行缓存数据重建
把新数据写入缓存中
最后释放锁
添加互斥锁可以保证
同时只存在一个线程对数据库进行缓存数据重建
如果在缓存数据重建中查询的线程会进入休眠等待数据重建
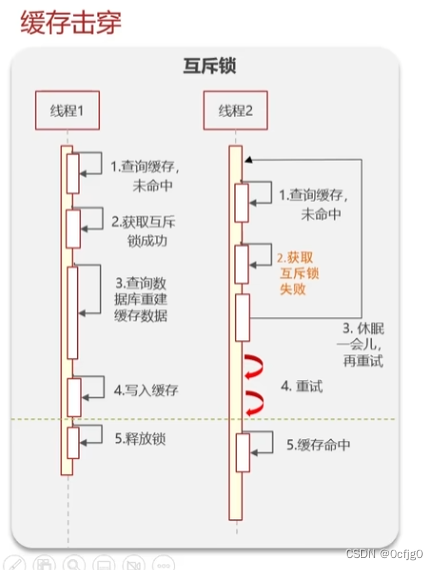
性能较低,但一致性好
逻辑过期
不设置过期时间使用逻辑过期
通过过期时间字段来定义数据的过期时间
过期时间在新增和更新时进行维护
当查询缓存时,发现数据已经过期
就会通过获取互斥锁的方式对数据进行重建
但重建数据使用新线程,在新线程完成数据重建后释放锁
原本查询缓存的线程会正常返回过期数据
其他查询的线程如果获取互斥锁失败(正在重建)也会正常返回过期数据
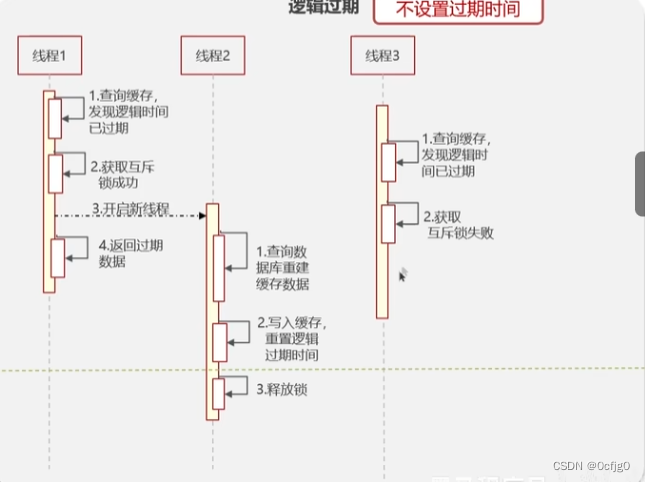
性能较高,但不能保证一致性
相关文章：
Java面试题:解决Redis缓存击穿问题
缓存击穿 当一个key过期时,需要对这个key进行数据重建 在重建的时间内如果有大量的并发请求进入,就会绕过缓存进入数据库,会瞬间击垮DB 重建时间可能因为数据是多个表的混合结果需要分头统计而延长,从而更容易出现缓存击穿问题 缓存击穿的解决方案 添加互斥锁 先查询缓存…...
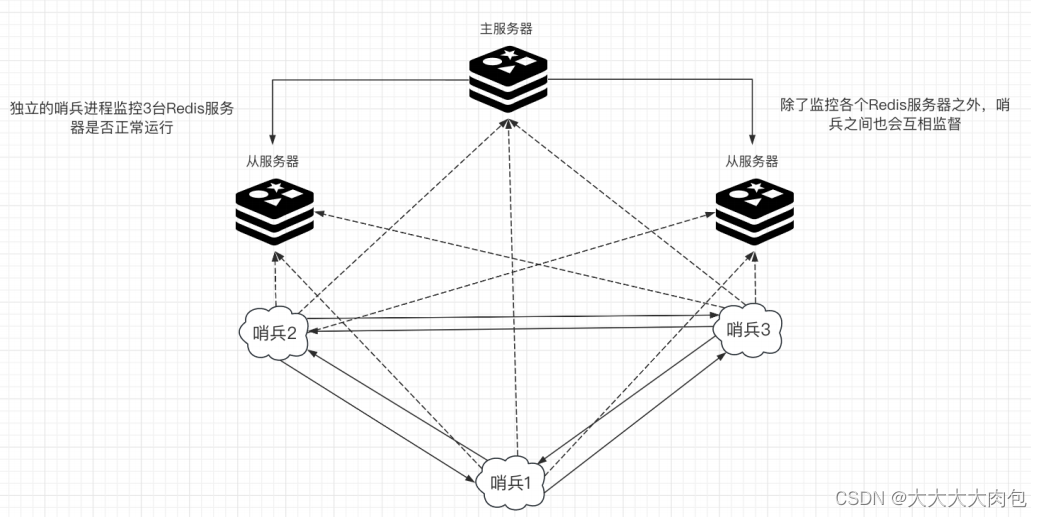
Redis的哨兵模式
什么是哨兵模式 Redis的哨兵模式（ Sentinel mode ）是⼀个⾼可⽤解决⽅案，当运⾏多个 Redis 实例并且需要⾃动故障转移时，哨兵模式⾮常有⽤。 在⼀个典型的哨兵模式下，⾄少需要3 个哨兵实例来避免 “ 脑裂 ” ÿ…...
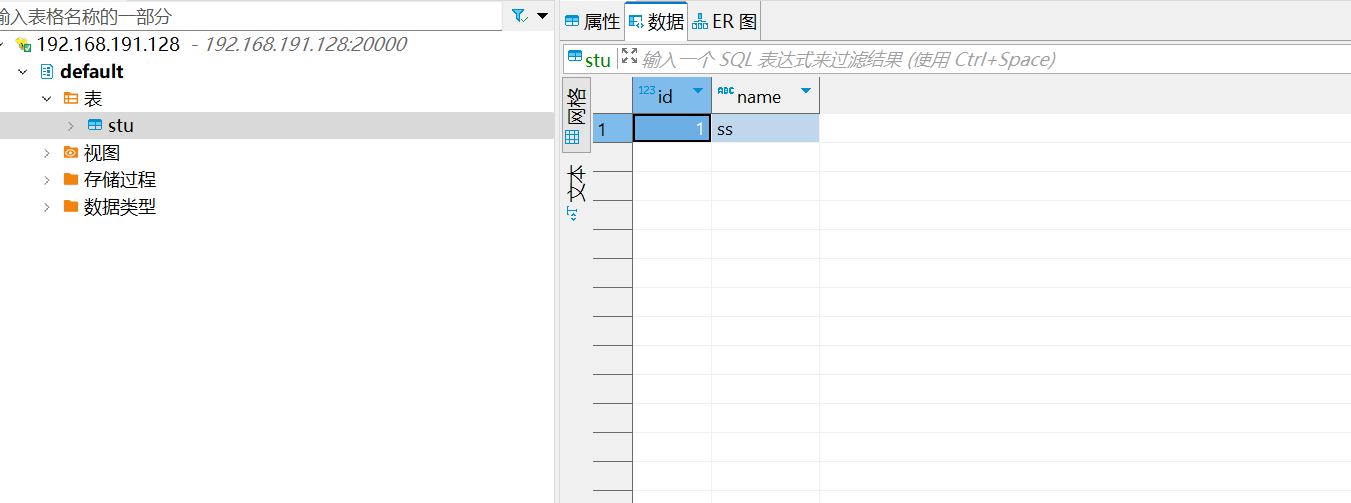
Hadoop伪分布式安装教程
Hadoop伪分布式安装教程 一、安装背景1.1 软件列表1.2 系统软件列表 二、安装Hadoop2.1 安装 Java 环境2.1.1 前期准备2.1.2 文件传输2.1.3 解压文件2.1.4 配置 jdk 的环境变量2.1.5 输入 java、javac、java -version 命令检验 jdk 是否安装成功 2.2 Hadoop 下载地址[hadoop](h…...
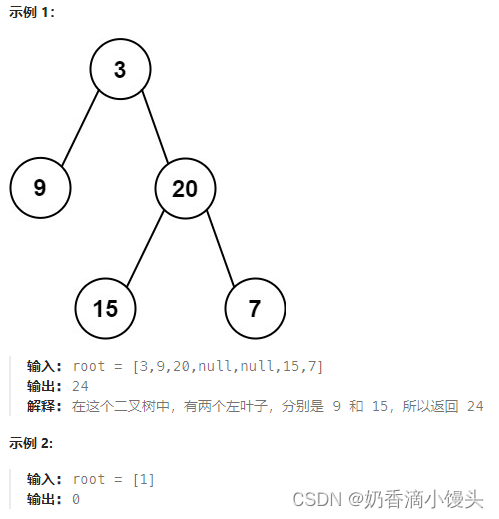
Day43 代码随想录打卡|二叉树篇---左叶子之和
题目（leecode T404）： 给定二叉树的根节点 root ，返回所有左叶子之和。 方法： 迭代法：计算所有的左叶子节点，那我们就必然要找到所有的左叶子节点。那么怎么找呢？如何针对cur->l…...
微信小程序动画
微信小程序动画属性：提升用户体验的利器 引言 随着移动互联网技术的快速发展，微信小程序已经成为开发者和用户的热门选择。其轻便、快捷、即用即走的特点使得它在各种场景中都有广泛的应用。而动画作为一种重要的视觉元素，在增强用户体验方…...
js， ellipsis属性， 超出宽度自动省略... ， 并且显示2行
overflow:hidden; display:-webkit-box; -webkit-line-clamp:2; -webkit-box-orient:vertical; text-overflow:ellipsis;...
ucharts自定义添加tooltip悬浮框显示项内容且换行
欢迎点击领取 -《前端开发面试题进阶秘籍》：前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 一、需求描述分析 1、小程序上实现图表的绘制，多条线路，不同颜色，悬浮框对应内容不同数据进行处理 2…...
Mongo 地理位置查询：海量密集点转换成聚合信息
通俗来说：将地图上的海量密集点通过网格分割的方式实现聚合； 需求：用mongo实现设备地理位置聚合查询 ：多边形，矩形查询; 背景：上万设备数据量 目的：分享Mongo地理位置查询，以及文…...
bpmn+vue 中文文档
1.初始化项目 <script> import BpmnModeler from bpmn-js/lib/Modeler import { xmlStr } from /mock/xmlStr export default {mounted () {this.init()},methods: {init () {// 获取到属性ref为“canvas”的dom节点const canvas this.$refs.canvas// 建模const custom…...
React Router v5 和 v6 中，路由对象声明方式有什么区别？
一、在React Router 6.x开始，路由对象的声明需要引用RouteObject。 import { RouteObject } from react-router-dom;const routes: RouteObject[] [{path: /,element: <Home />},{path: /about,element: <About />},// ... ];二、一些老项目使用的是R…...
【全开源】知识库文档系统（ThinkPHP+FastAdmin）
📚知识库文档系统：解锁知识的无限可能 一款基于ThinkPHPFastAdmin开发的知识库文档系统，可用于企业工作流程的文档管理，结构化记录沉淀高价值信息，形成完整的知识体系，能够轻松提升知识的流转和传播效率&a…...
Python赋能自然语言处理，解锁通往AI的钥匙
NLTK（Natural Language Toolkit）是一个用于 Python 的自然语言处理库,提供了丰富的工具和资源,帮助处理、分析和理解人类语言数据.它广泛应用于学术研究、教育和商业应用中. 安装 #首先要安装 NLTK：pip install nltk安装完成后,还需要下载…...
Ktor库的高级用法：代理服务器与JSON处理
在现代网络编程中，Ktor是一个高性能且易于使用的框架，它提供了对异步编程、WebSockets、HTTP客户端和服务器等特性的原生支持。Ktor是使用Kotlin语言编写的，充分利用了Kotlin的协程特性来简化异步编程。本文将深入探讨Ktor库的高级用法&#…...
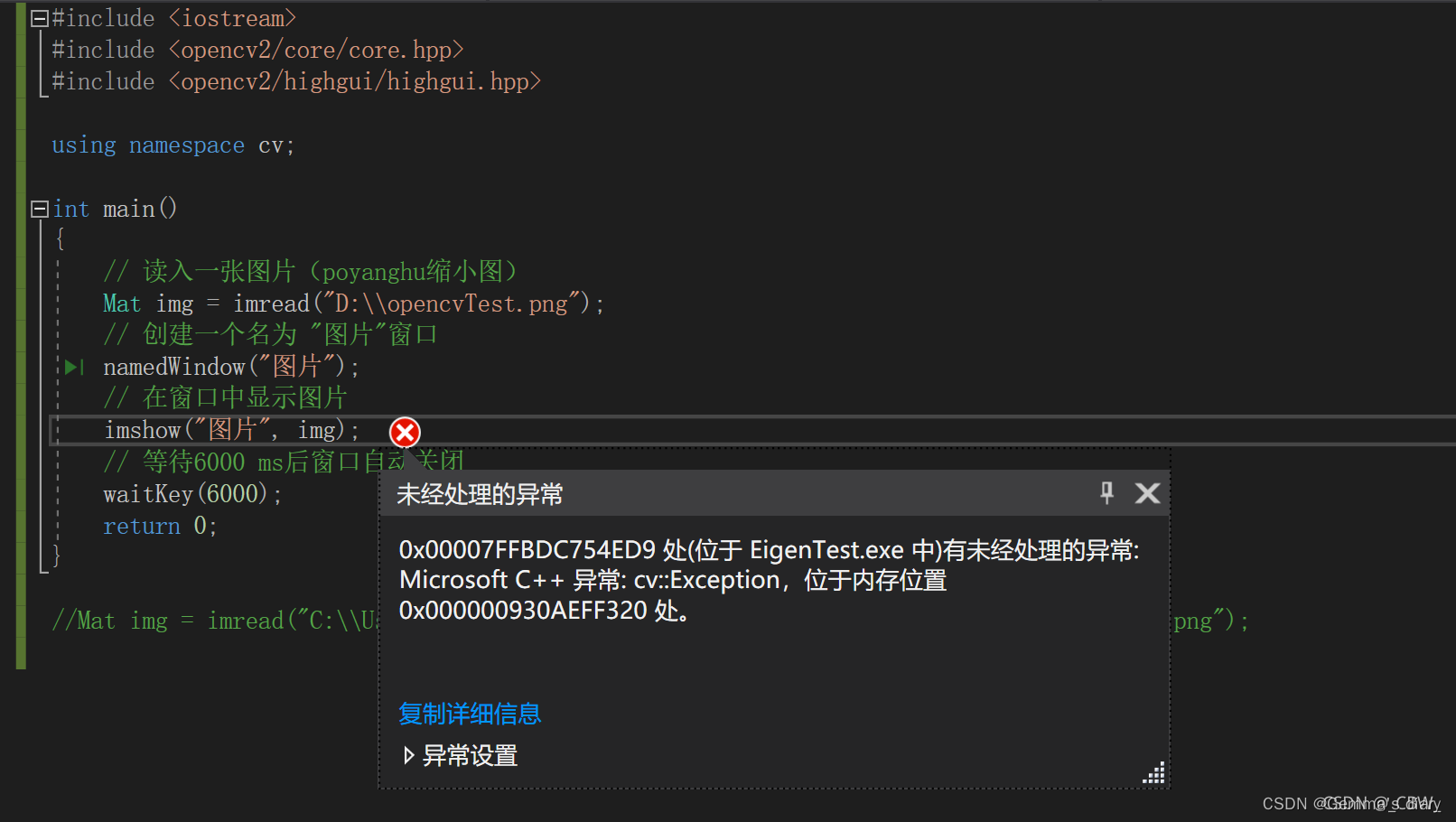
VS2017配置OpenCV4.5.1
VS2017配置OpenCV 一、下载OpenCV二、配置OpenCV的电脑环境变量三、配置visual Studio添加路径复制文件到C盘 四、如何使用注意运行时选择Debug x64 五、报错：VSOpencv出现：xxx处有未经处理的异常: Microsoft C 异常: cv::Exception，位于内存…...
phpstudy配置的站点不能访问了
无法打开站点 打开网站的时候出现如下 没有人为主动去更改配置项，今天就不能正常访问了 检查了一遍配置，发现并无大碍，那就重新配置一遍看看 配置phpstudy 1、新建网站 2、选择项目入口文件夹 3、配置伪静态 4. 确认保存 在我的电脑 C:\…...
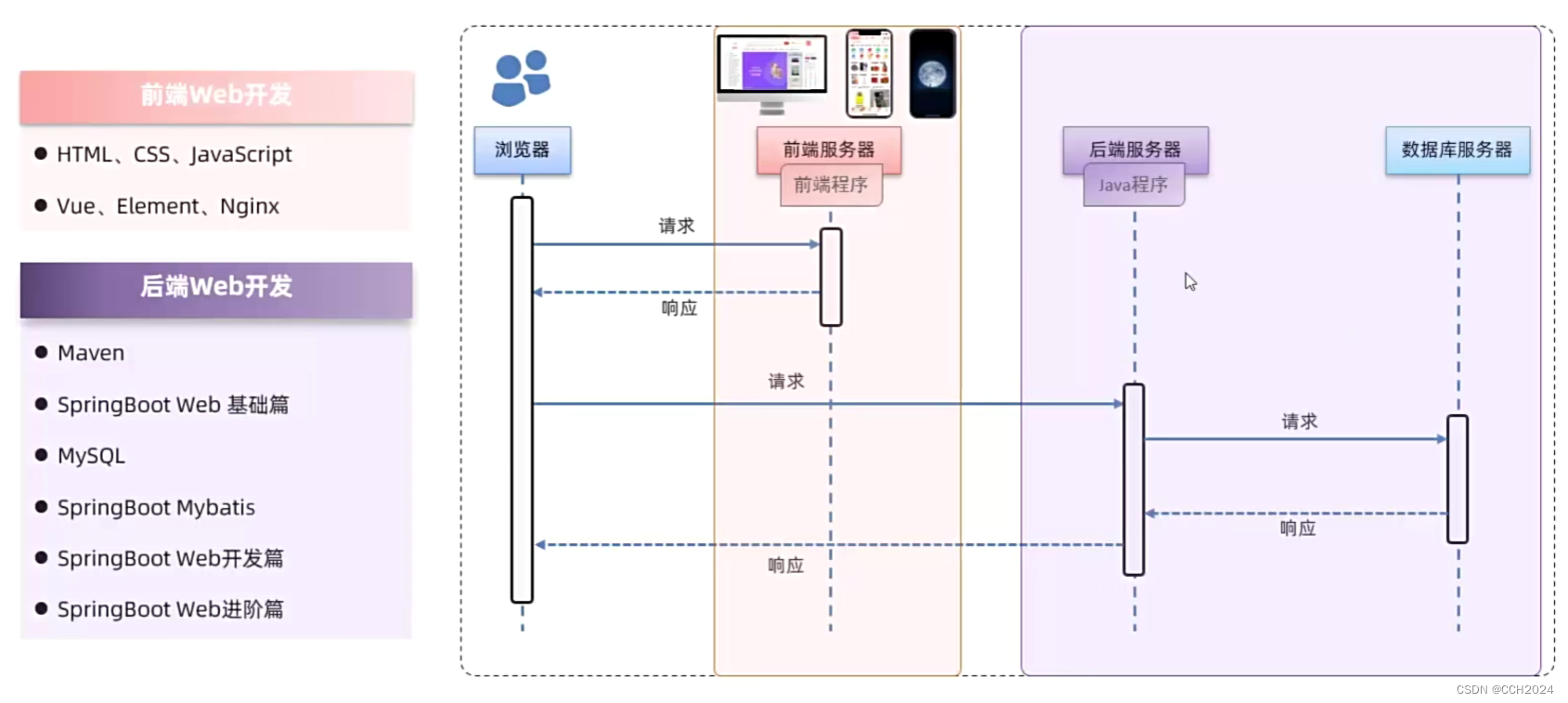
Java Web学习笔记2——Web开发介绍
什么是Web？ Web：全球广域网，也称为万维网（WWW World Wide Web），能够通过浏览器访问的网站。 1）淘宝、京东、唯品会等电商系统； 2）CRM、OA、ERP企业管理系统࿱…...
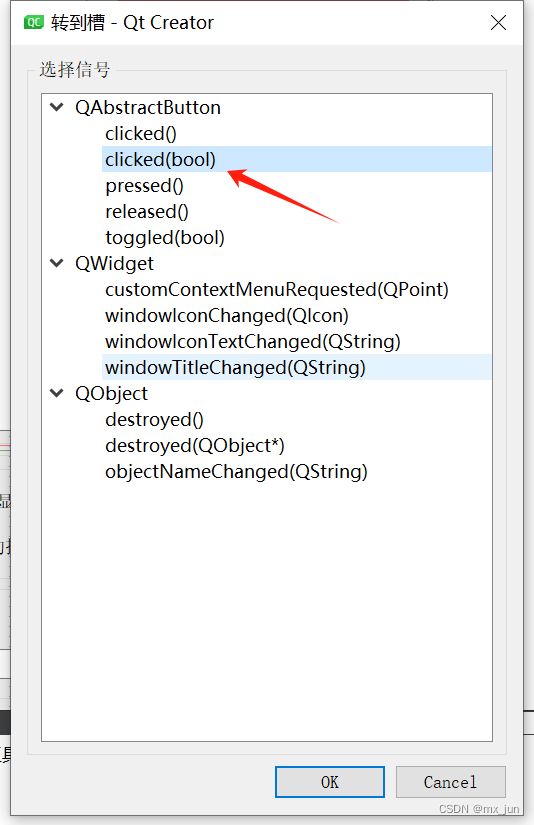
从零开始实现自己的串口调试助手(3) - 显示底部收发，优化串口打开/关闭
注意: 1. 我们要实现自发自收，要将tx，rx连起来 2.发送的 不能是中文符号，因为这可能导致，读取到的是英文符号 --> 导致接收到的size 和发送的size 大小不一致 3.注意同时定义两个槽函数的时候两个槽函数都会被调用，…...
更改Web网站设计——css和css框架
虽然使用HTML可以定义文章的结构，但是其中不包含设计相关的信息。此时CSS就派上用场，可以用它对HTML文章指定设计样式。由于可以决定Web网页的外观风格，因此，它有时也被称为格式表。 如果使用CSS设置背景色，文…...
持续监控和优化的简单介绍
DevOps 监控提供了有关生产环境状况的全面且最新的信息，以及有关其服务、基础设施和应用程序的详细信息。通过从日志和指标中收集数据，您可以在软件开发生命周期的每个步骤中监控合规性和性能。 监控不仅仅针对生产问题，它涵盖了规划、开发、…...
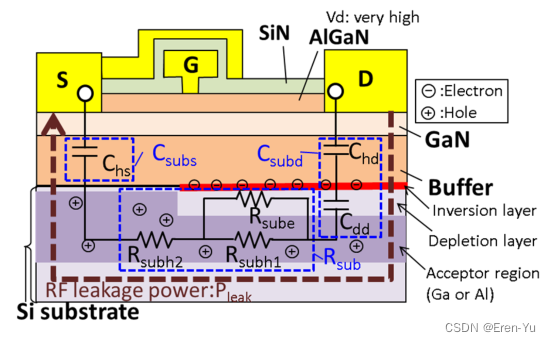
针对硅基氮化镓高电子迁移率晶体管(GaN-HEMT)的准物理等效电路模型，包含基板中射频漏电流的温度依赖性
来源：Quasi-Physical Equivalent Circuit Model of RF Leakage Current in Substrate Including Temperature Dependence for GaN-HEMT on Si（TMTT 23年） 摘要 该文章提出了一种针对硅基氮化镓高电子迁移率晶体管（GaN-HEMT&…...
UE5 学习系列（二）用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇，在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下： 【Note】：如果你已经完成安装等操作，可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作，重…...
＜6＞-MySQL表的增删查改
目录 一，create（创建表） 二，retrieve（查询表） 1，select列 2，where条件 三，update（更新表） 四，delete（删除表…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log，共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题，不能使用ELK只能使用…...
oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异，它们的数据同步要求既要保持数据的准确性和一致性，又要处理好性能问题。以下是一些主要的技术要点： 数据结构差异 数据类型差异ÿ…...
什么？连接服务器也能可视化显示界面？：基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11？环境准备实战步骤1️⃣ 服务器端配置（CentOS）2️⃣ 客户端配置（MobaXterm）3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中，部分节点存储的数据量或访问量远高于其他节点，导致这些节点负载过高，影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代，加密货币作为一种新兴的金融现象，正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而，加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下，稳定…...
Linux --进程控制
本文从以下五个方面来初步认识进程控制： 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程，创建出来的进程就是子进程，原来的进程为父进程。…...