代码随想录算法训练营day29|491.递增子序列、46.全排列、47.全排列II
递增子序列
491. 非递减子序列 - 力扣(LeetCode)
非递减子序列,则答案的子集中,需保持下一个元素大于等于前一个元素的顺序,由于题目中指出,所有的子序列长度需大于等于2,考虑当条件为path.size()>1时,进行收获结果,且需要注意,这时不应该直接return,因为后续仍有可能存在子序列长度大于2的结果,仍需要继续遍历。此时结束的标志是单层遍历的结束。
如果只按照上述向下运行,没有完成子序列的去重操作,为了完成子序列的去重以及保证下一个元素大于当前元素才加入数组,考虑加入一个set,在对当前层进行遍历时,若该元素没有使用过,将其加入set,若该元素大于path的末尾元素,将其加入path。之后继续回溯,回溯完成后复原path。具体思路参考代码随想录。
代码随想录 (programmercarl.com)![]() https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
class Solution {
public:vector<int> path; // 存储当前递增子序列vector<vector<int>> paths; // 存储所有不同的递增子序列void backtracking(vector<int>& nums, int start) {if (path.size() >= 2) {paths.push_back(path); // 将满足条件的子序列添加到结果中}unordered_set<int> uset; // 用于去重for (int i = start; i < nums.size(); ++i) {if ((!path.empty() && nums[i] < path.back()) || uset.find(nums[i]) != uset.end()) {continue; // 跳过不满足条件的元素}uset.insert(nums[i]);path.push_back(nums[i]);backtracking(nums, i + 1); // 递归搜索下一个元素path.pop_back(); // 回溯,移除当前元素}}vector<vector<int>> findSubsequences(vector<int>& nums) {backtracking(nums, 0); // 从第一个元素开始搜索return paths;}
};
回溯法寻找递增子序列的过程,在最差情况下需要遍历所有可能的子序列,每个元素都有可能存在或者不存在与子序列中,所以算法的时间复杂度为O(2^n),就空间复杂度来说,使用了哈希集合来检查是否已经包含了某个元素,使用了一个辅助的path来存储当前的子序列,在递归的过程中,path和uset都会不断改变,但最大的情况为递归的最深处,此时应有n层,因此空间复杂度为O(n)。
全排列
46. 全排列 - 力扣(LeetCode)
思路:从数组的第一个元素开始,逐步构建排列,对于每个位置,将不同的数字放在该位置上,然后递归地处理下一个位置。若当前位置已经包含了某元素,则我们要跳过它,选择其他数字,条件为
if (find(path.begin(), path.end(), nums[i]) == path.end()) 治理find函数返回的迭代器等于path.end(),说明nums[i]不在path中,即当前数字还没有被使用过。
当排列的长度等于数组的长度时,收获为一个有效的排列。
if (path.size() == nums.size()) {result.push_back(path); // 当排列长度等于数组长度时,保存该排列return;}整体代码如下。
class Solution {
public:vector<int> path; // 保存当前排列vector<vector<int>> result; // 保存所有不同的排列void backtracking(vector<int>& nums, int start) {if (path.size() == nums.size()) {result.push_back(path); // 当排列长度等于数组长度时,保存该排列return;}for (int i = 0; i < nums.size(); ++i) {if (find(path.begin(), path.end(), nums[i]) == path.end()) {// 如果当前数字不在排列中,将其添加到排列中path.push_back(nums[i]);backtracking(nums, i + 1); // 递归搜索下一个位置path.pop_back(); // 回溯,移除当前数字}}}vector<vector<int>> permute(vector<int>& nums) {backtracking(nums, 0); // 从第一个位置开始搜索return result;}
};排列的时间复杂度为O(n!),每个位置,都可以选择不同的数字。
空间复杂度为O(n)。
全排列II
47. 全排列 II - 力扣(LeetCode)
错误代码,使用了start
class Solution {
public:vector<int> path; // 保存当前排列vector<vector<int>> result; // 保存所有不同的排列void backtracking(vector<int>& nums, int start) {if (path.size() == nums.size()) {result.push_back(path); // 当排列长度等于数组长度时,保存该排列return;}for (int i = 0; i < nums.size(); ++i) {if(start > 0 and nums[i]== nums[i - 1]){continue;}path.push_back(nums[i]);backtracking(nums, i + 1); // 递归搜索下一个位置path.pop_back(); // 回溯,移除当前数字}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end()); // 首先排序,以便去除重复排列backtracking(nums, 0);return result;}
};正确代码
class Solution {
public:vector<int> path; // 保存当前排列vector<vector<int>> result; // 保存所有不同的排列void backtracking(vector<int>& nums, vector<bool>& used, int start) {if (path.size() == nums.size()) {result.push_back(path); // 当排列长度等于数组长度时,保存它return;}for (int i = 0; i < nums.size(); ++i) {if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue; // 跳过重复的元素}if (!used[i]) {path.push_back(nums[i]);used[i] = true;backtracking(nums, used, i + 1); // 递归搜索下一个位置path.pop_back(); // 回溯,移除当前数字used[i] = false;}}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end()); // 首先排序,以便去除重复排列vector<bool> used(nums.size(), false); // 初始化 used 数组backtracking(nums, used, 0);return result;}
};
start可有可无
算法的时间复杂度为O(n!),空间复杂度为O(n),同上。
相关文章:
代码随想录算法训练营day29|491.递增子序列、46.全排列、47.全排列II
递增子序列 491. 非递减子序列 - 力扣(LeetCode) 非递减子序列,则答案的子集中,需保持下一个元素大于等于前一个元素的顺序,由于题目中指出,所有的子序列长度需大于等于2,考虑当条件为path.siz…...

【ARM Cache 与 MMU 系列文章 7.8 – ARMv8/v9 MMU Table 表分配原理及其代码实现 2】
请阅读【ARM Cache 及 MMU/MPU 系列文章专栏导读】 及【嵌入式开发学习必备专栏】 文章目录 MMU Table 表分配原理及其代码实现MMU Table 分配代码实现MMU Table 表分配原理及其代码实现 在做映射的时候所映射的地址范围最大只能是某一级 level table 中 entry 所能支持的最大…...
SAP PP学习笔记17 - MTS(Make-to-Stock) 按库存生产(策略70)
上几章讲了几种策略,策略10,11,30,40。 SAP PP学习笔记14 - MTS(Make-to-Stock) 按库存生产(策略10),以及生产计划的概要-CSDN博客 SAP PP学习笔记15 - MTS(Make-to-St…...
网页音频提取在线工具有哪些 网页音频提取在线工具下载
别再到处去借会员账号啦。教你一招,无视版权和地区限制,直接下载网页中的音频文件。没有复杂的操作步骤,也不用学习任何代码。只要是网页中播放的音频文件,都可以把它下载到本地保存。 一、网页音频提取在线工具有哪些 市面上的…...

【ARM Cache 系列文章 2.1 -- Cache PoP 及 PoDP 介绍】
请阅读【ARM Cache 及 MMU/MPU 系列文章专栏导读】 及【嵌入式开发学习必备专栏】 文章目录 PoP 及 PoDPCache PoDPCache PoP应用和影响PoP 及 PoDP Cache PoDP 点对深度持久性(Point of Deep Persistence, PoDP)是内存系统中的一个点,在该点达到的任何写操作即使在系统供电…...

一文了解JVM面试篇(上)
Java内存区域 1、如何解释 Java 堆空间及 GC? 当通过 Java 命令启动 Java 进程的时候,会为它分配内存。内存的一部分用于创建 堆空间,当程序中创建对象的时候,就从对空间中分配内存。GC 是 JVM 内部的一 个进程,回收无效对象的内存用于将来的分配。 2、JVM 的主要组成…...

C#WPF控件Textbox绑定浮点型数据限制小数位方法
本文讲解C#WPF控件Textbox绑定浮点型数据限制小数位方法。 XAML中,使用StringFormat来格式化TextBox的文本 <Window x:Class="WpfApp.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.m…...
mysql引入表名称的注意事项
1、遇到问题 mapper中的文件是这样的 解析出来的sql是这样的 sql显示为:select * from ‘tableName’ 2、解决方法 mapper文件种使用${tableName}而不是#{tableName}...
C语言数据结构快速排序的非递归、归并排序、归并排序的非递归等的介绍
文章目录 前言一、快速排序非递归二、归并排序五、归并排序非递归总结 前言 C语言数据结构快速排序的非递归、归并排序、归并排序的非递归等的介绍 一、快速排序非递归 快速排序非递归的定义 快速排序非递归,需要使用栈来实现。将左右下标分别push到栈中。在栈为…...

学生成绩管理系统(大一大作业)
功能 实现添加,排序,修改,保存等功能 库函数 #include<stdio.h> #include<stdlib.h> #include<windows.h> #include<string.h> 头文件 #define functioncreate(major) void major##compare(mana mn){\int i,j,s…...
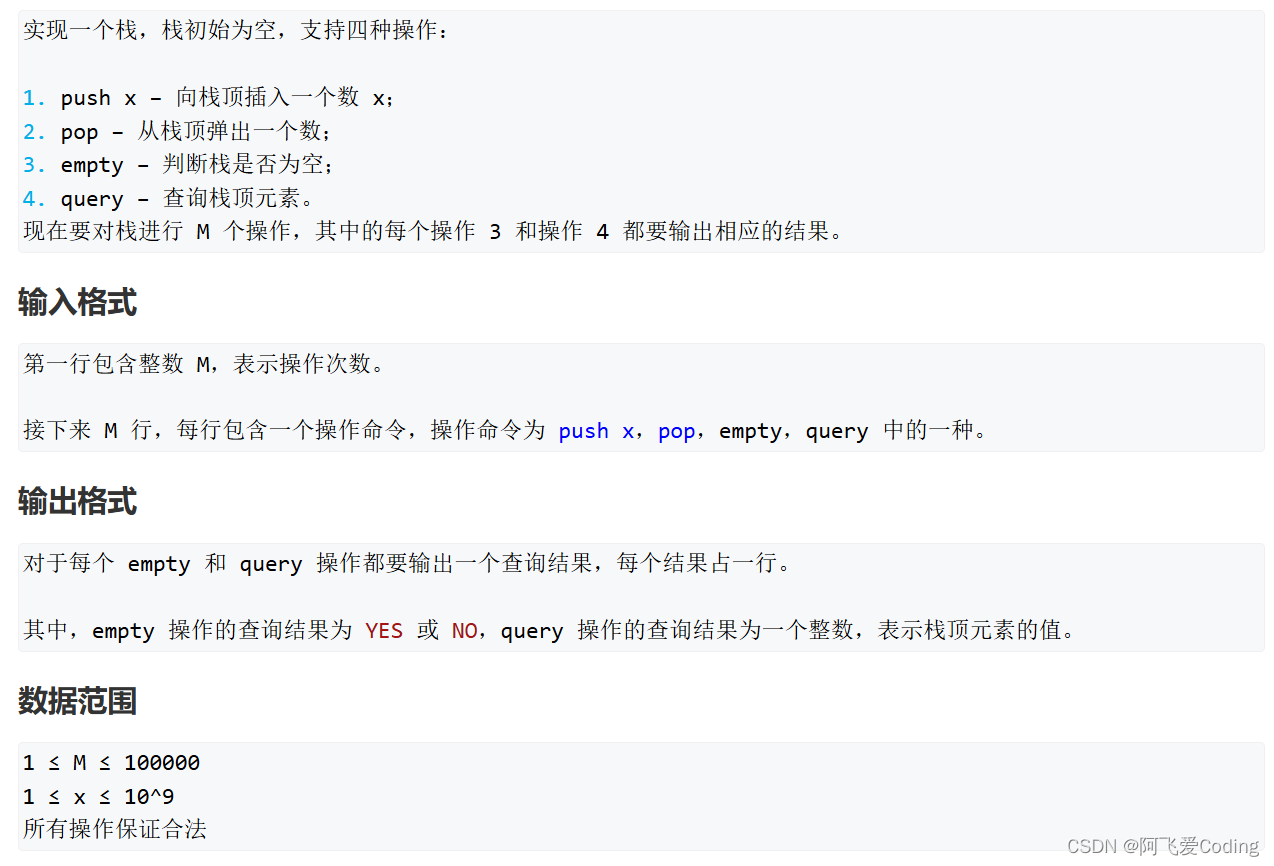
数据结构:模拟栈
数据结构:模拟栈 题目描述参考代码 题目描述 输入样例 10 push 5 query push 6 pop query pop empty push 4 query empty输出样例 5 5 YES 4 NO参考代码 #include <iostream>using namespace std;const int N 1000010;int m, x; int q[N]; string op; int…...

02-2.3.6 顺序表和链表的比较
喜欢《数据结构》部分笔记的小伙伴可以订阅专栏,今后还会不断更新。🧑💻 此外,《程序员必备技能》专栏和《程序员必备工具》专栏(该专栏暂未开设)日后会逐步更新,感兴趣的小伙伴可以点一下订阅…...
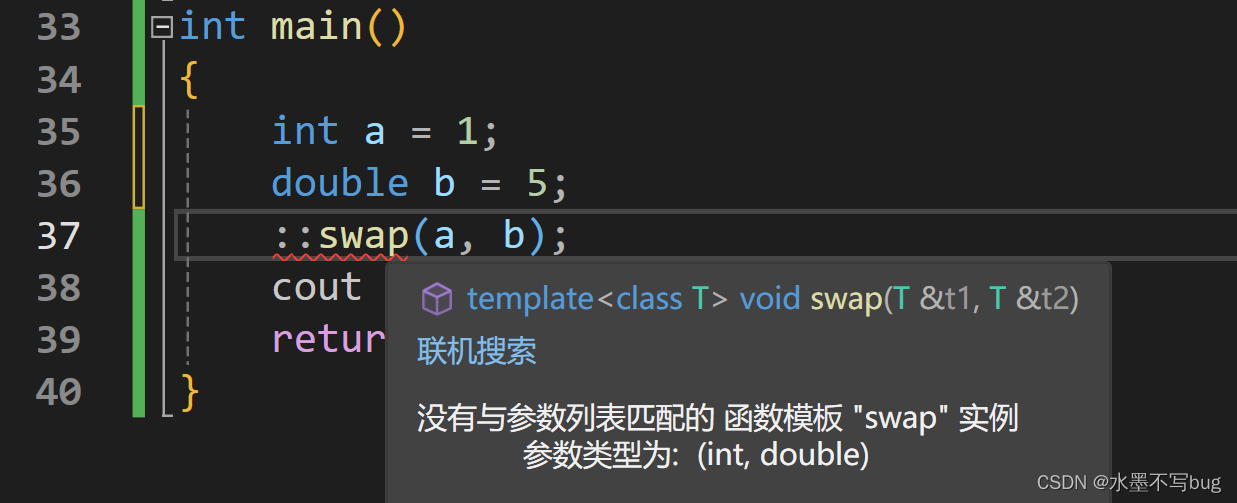
C++ : 模板初阶
标题:C : 模板初阶 水墨不写bug 正文开始: C语言的问题 : 写不完的swap函数 在学习C语言时,我们有一个经常使用的函数swap函数,它可以将两个对象的值交换。 我们通常这样实现它: void swap(int t1,int t2)…...

FFA-Net:用于单图像去雾的特征融合注意力网络
摘要 论文链接:https://arxiv.org/pdf/1911.07559v2 在这篇论文中,我们提出了一种端到端的特征融合注意力网络(FFA-Net)来直接恢复无雾图像。FFA-Net架构由三个关键组件组成: 一种新颖的特征注意力(FA&…...

网工内推 | 联通公司,云计算售前,AWS认证优先
01 联通数字科技有限公司 🔷招聘岗位:云计算售前工程师 🔷职责描述: 1.了解私有云,公有云,混合云等云计算技术知识,了解云计算行业现状及发展趋势。 2.承担区域项目售前工作支持,为…...

[Redis]Zset类型
Zset有序集合相对于字符串、列表、哈希、集合来说会有一些陌生。 它保留了集合不能有重复成员的特点,但与集合不同的是,有序集合中的每个元素都有一个唯一的浮点类型的分数(score)与之关联,着使得有序集合中的元素是可…...
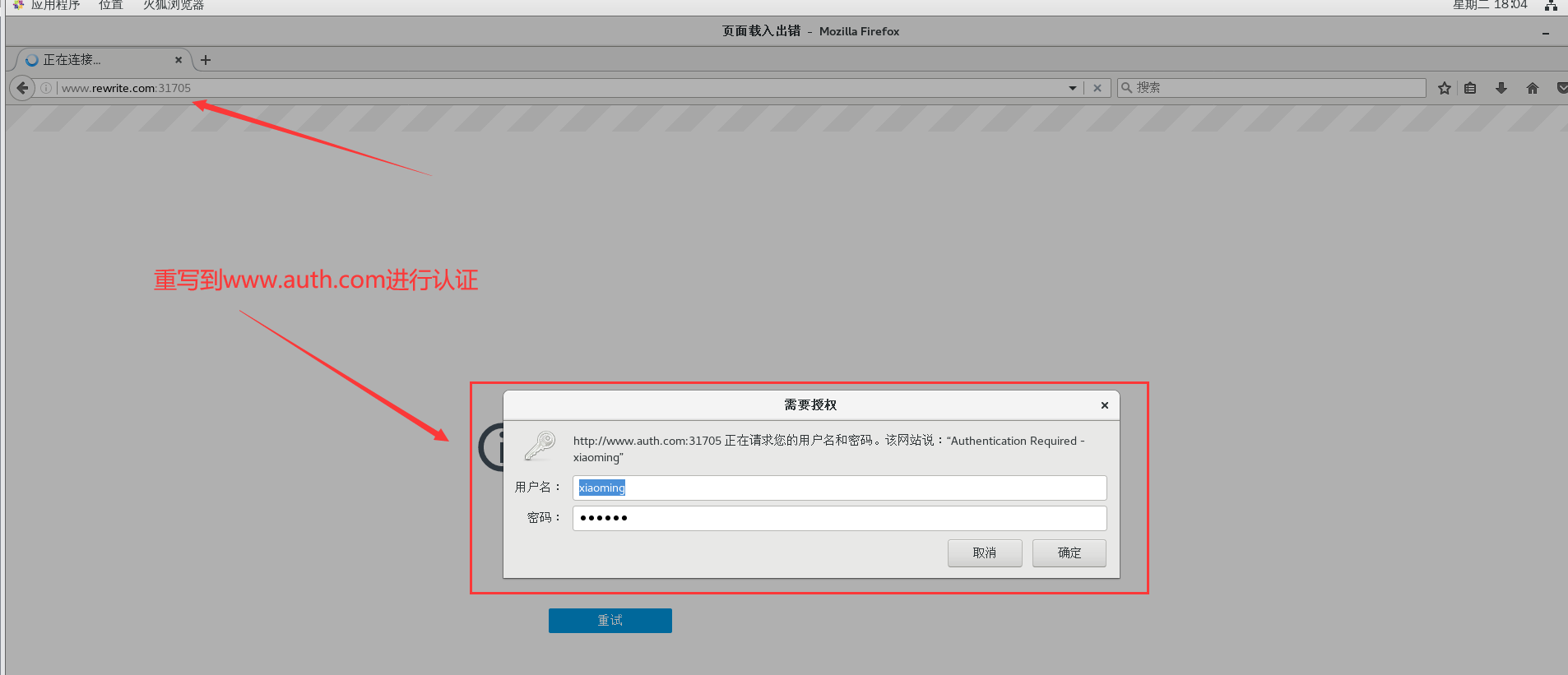
【云原生】Kubernetes----Ingress对外服务
目录 引言 一、K8S对外方式 (一)NodePort 1.作用 2.弊端 3.示例 (二)externalIPs 1.作用 2.弊端 3.示例 (三)LoadBalancer 1.作用 2.弊端 (四)Ingress 二、Ingress的…...

项目管理之maven svn
管理jar包之间依赖关系 编译、打包、清理、测试等一系列构建工具 一、Maven的标志 1、每一个maven工程都有一个pom.xml maven项目坐标 <groupId>com.aaa</groupId>//项目路径 <artifactId>web</artifactId>项目名称 <version>0.0.1-SNAPS…...
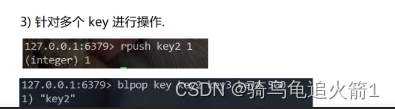
Redis篇 list类型在Redis中的命令操作
list在redis基本的命令 一.基本命令1.lpush和range2.lpushx rpushx3.lpop rpop4.lindex linsert llen5.lrem6.ltrim lset7.blpop brpop 一.基本命令 list在redis中相当于数组或者顺序表. 1.lpush和range 2.lpushx rpushx 3.lpop rpop 4.lindex linsert llen 如果要插入的列表中…...
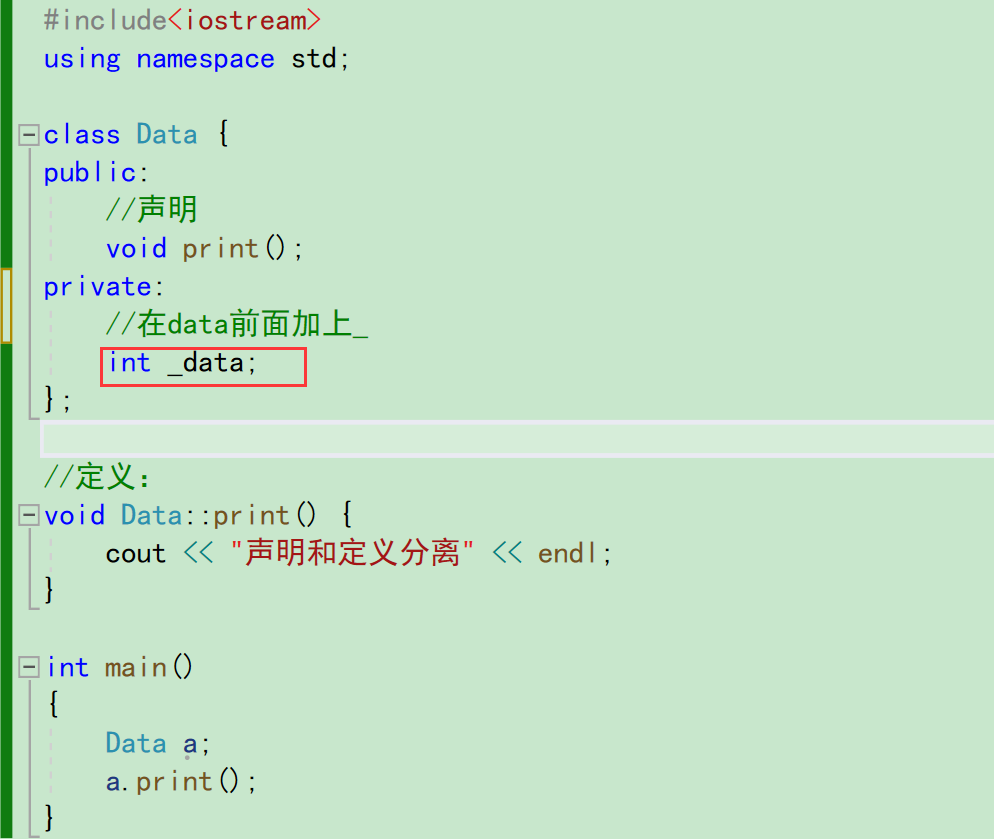
【C++课程学习】:类和对象(上)(类的基础详细讲解)
🎁个人主页:我们的五年 🔍系列专栏:C课程学习 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 🍟1.1类的引出: 🍟1.2类的结构: 🍟1.3类的…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
