零钱兑换 - LeetCode 热题 85
大家好!我是曾续缘🤪
今天是《LeetCode 热题 100》系列
发车第 85 天
动态规划第 5 题
❤️点赞 👍 收藏 ⭐再看,养成习惯
零钱兑换 给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1示例 2:
输入:coins =[2], amount =3输出:-1示例 3:
输入:coins = [1], amount = 0 输出:0提示:
难度:💖💖
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
解题方法
我们可以使用动态规划来解决这个问题。首先创建一个长度为 amount + 1 的数组 dp,其中 dp[i] 表示凑齐金额 i 所需要的最少硬币个数。初始化将 dp 数组所有元素值设为 amount + 1,这个值相当于无穷大,用来表示不可能凑齐该金额。
然后,我们从金额 1 开始遍历到 amount,对于每个金额 i,再遍历硬币数组 coins 中的每个硬币面额 coins[j]。如果当前硬币面额 coins[j] 小于等于当前金额 i,则更新 dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1),即当前金额 i 所需的最少硬币个数为当前值和减去当前硬币面额后的金额所需硬币个数加一的较小值。
最终返回 dp[amount],如果其值大于 amount,表示无法凑齐该金额,返回 -1;否则返回 dp[amount]。
Code
public class Solution {public int coinChange(int[] coins, int amount) {// 初始化最大值为 amount + 1int max = amount + 1;// 创建 dp 数组,记录凑齐各个金额所需的最少硬币个数int[] dp = new int[amount + 1];// 将 dp 数组所有元素值设为 maxArrays.fill(dp, max);// 初始金额为 0 时,所需硬币个数为 0dp[0] = 0;// 遍历金额从 1 到 amountfor (int i = 1; i <= amount; i++) {// 遍历硬币数组for (int j = 0; j < coins.length; j++) {// 如果当前硬币面额小于等于当前金额if (coins[j] <= i) {// 更新最少硬币个数dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}// 返回最终结果,若大于 amount 则无法凑齐,返回 -1,否则返回 dp[amount]return dp[amount] > amount ? -1 : dp[amount];}
}相关文章:

零钱兑换 - LeetCode 热题 85
大家好!我是曾续缘🤪 今天是《LeetCode 热题 100》系列 发车第 85 天 动态规划第 5 题 ❤️点赞 👍 收藏 ⭐再看,养成习惯 零钱兑换 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount &…...

基于web的垃圾分类回收系统的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,用户管理,公告管理,运输管理,基础数据管理 用户账户功能包括:系统首页,个人中心,运输管理,公告…...
优化你的WordPress网站:内链建设与Link Whisper Pro插件的利用
文章目录 内链的重要性WordPress SEO插件:Link Whisper Pro主要功能使用指南下载与安装 结语 在数字营销和网站管理领域,SEO内部优化是提升网站排名、增加流量和提高用户参与度的核心策略。在众多SEO技巧中,内链建设是构建良好网站结构和提升…...

spring中那些地方使用了反射
1、依赖注入(Dependency Injection) Spring Boot通过反射机制将bean注入到相应的属性或构造函数中。当我们在Spring Boot中使用如Autowired这样的注解时,Spring容器会利用反射机制找到相应的bean并注入到对应的属性或构造函数中。 2、Bean的…...

1 机器人软件开发学习所需通用技术栈(一)
机器人软件工程师技术路线(如有缺失,欢迎补充) 1. 机器人软件开发工程师技术路线 1.1 基础知识 C/C编程:掌握C/C语言基础,包括数据结构、算法、内存管理等。操作系统:了解Linux或Windows等操作系统的基本…...

Java(十二)——Comparable接口与Comparator接口
文章目录 Comparable与Comparator接口Comparable接口Comparator接口 Comparable与Comparator接口 我们可能会遇到这样的问题:怎么对一个对象数组进行排序? 比如对一个狗类对象数组进行排序,而想到这,我们又会有一个问题ÿ…...

Nvidia Jetson/Orin +FPGA+AI大算力边缘计算盒子:轨道交通监控系统
株洲中车时代电气股份有限公司(下称中车时代电气)是中国中车旗下股份制企业,其前身及母公司——中车株洲电力机车研究所有限公司创立于1959年。中车时代电气扎根株洲,走好两条钢轨,走出两条钢轨。中车时代电气秉承“双…...

笔记 | 软件工程01:从程序到软件
1 软件工程知识域 2 程序 2.1 何为程序及程序的质量要求 何为程序: 理解:软件工程可能就是在弥补OOP语言与自然语言之间还存在的鸿沟 2.1.1 程序质量的内在和外在体现 2.1.2 程序质量的语法和语义体现 2.2 编写代码的基本原则 2.3 程序质量保证方法 …...

废品回收小程序开发,助力商家拓展回收市场
随着互联网的快速发展,废品回收行业也走向了数字化发展,废品回收小程序成为了拓展市场的重要方式。在当下万亿元下的回收市场中,废品回收小程序的发展也能够发挥重要作用,提高市场回收效率,提高大众的回收意识…...
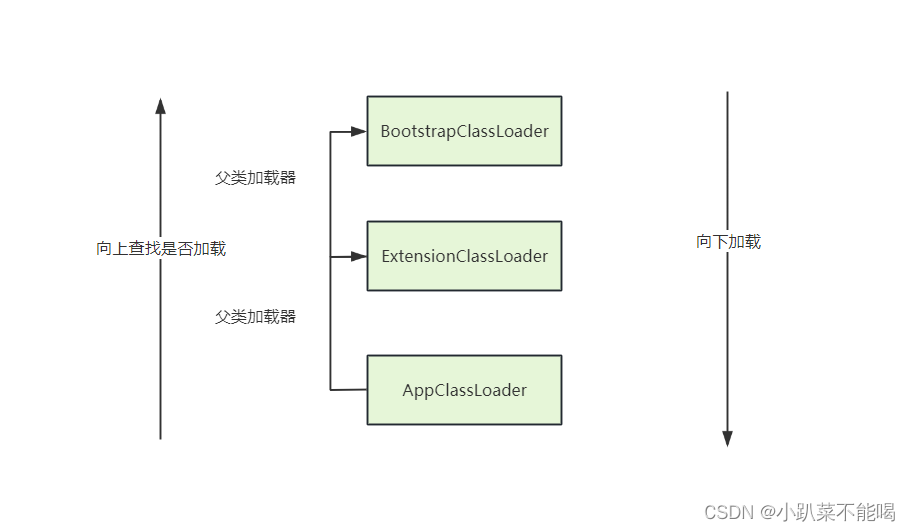
JVM类加载机制和双亲委派
类加载机制 java文件需要编译成字节码文件(.class文件),jvm是通过类加载机制,将.class文件加载进内存,经过验证连接->初始化直到使用该对象的过程就是类加载机制,当new对象的时候,jvm首先去常量池寻找该类的符号引用…...

【PyCharm】无法创建虚拟环境,提示:has no attribute CPython3macOsBrew
报错信息: AttributeError: module virtualenv.create.via_global_ref.builtin.cpython.mac_os has no attribute CPython3macOsBrew报错原因: 可能含有多个virtualenv,发生冲突了。 解决方法: 终端执行以下命令: p…...
)
华为OD刷题C卷 - 每日刷题 12(数组连续和,求最多可以派出多少支团队)
1、(数组连续和): 这段代码是解决“数组连续和”的问题。它提供了一个Java类Main,其中包含main方法和getResult方法,用于计算给定数组中有多少个连续区间的和大于等于给定值x。 main方法首先读取数组的长度n和阈值x&…...

2.1 初识Windows程序
Windows程序设计是一种面向对象的编程。Windows操作系统以数据结构的形式定义了大量预定义的对象作为操作系统的数据类型。Windows动态链接库提供了各种各样的API接口函数供Windows应用程序调用。一个Windows应用程序是运行在Windows操作系统之上的。这些API接口函数的调用所实…...

EDI系统的使用场景
EDI全称Electronic Data Interchange,中文名称是电子数据交换。EDI系统是专为企业间的电子数据传输而设计的,需要满足的基本功能包括:支持AS2、OFTP、SFTP等EDI传输协议,能够生成和解析符合X12、EDIFACT、VDA等EDI报文标准下的报文…...

韩国Neowine推出第三代强加密芯片ALPU-CV
推出第三代加密芯片;是ALPU系列中的高端IC;是一款高性能车规级加密芯片;其加密性更强、低耗电、体积小;使得防复制、防抄袭板子的加密性能大大提升,该芯片通过《AEC-Q100》认证,目前已经在国产前装车辆配件…...

golang结构与接口方法实现与交互使用示例
1.定义结构 // 结构定义 type VideoFrame struct {id inthead []bytelen int64data []byte } 2.实现结构方法 // 生成结构字段的get与set方法 // func (v *VideoFrame) Id() int {return v.id }func (v *VideoFrame) SetId(id int) {v.id id }func (v *VideoFrame) He…...
C# 判断字符串不等于空的示例
在C#中,要判断一个字符串是否不等于空(即它既不是null也不是空字符串""),方法有如下几种,如下。 方法1 使用逻辑运算符和string.IsNullOrEmpty方法 string myString "123"; // 假设要检查的字…...

直方图中最大的矩形
#include<iostream> #include<algorithm> using namespace std; const int N 100010; //l[i], r[i]表示第i个矩形的高度可向两侧扩展的左右边界 int h[N], q[N], l[N], r[N]; typedef long long LL; int main() { int n; while(scanf("%d"…...
分布式锁redisson
1:pom.xml添加依赖 <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-boot-starter</artifactId><version>3.21.1</version> </dependency>2-1:方法一:读取默认ym…...

将小爱音箱接入 ChatGPT 和豆包ai改造成专属语音助手
这个GitHub项目,mi-gpt,旨在将小爱音箱和米家设备与ChatGPT和豆包集成,有效地将这些设备转变为个性化语音助手。以下是对其功能和设置的详细分析: 主要特点 角色扮演:该项目允许小爱适应不同的角色,如伴侣…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
