Python 树状数组
树状数组(Binary Indexed Tree, BIT),又称为斐波那契堆,是一种数据结构,用于高效地解决以下问题:
- 单点更新:在数组的某个位置增加或减少一个值。
- 区间查询:查询数组中一段连续区间的元素之和。
树状数组的核心思想是使用一个数组来存储原数组的累积和,然后利用数组的偏移来快速计算区间和。这种数据结构在时间复杂度上具有优势,对于单点更新和区间查询,它们的时间复杂度都是 (O(\log n))。
以下是 Python 中实现树状数组的基本操作的示例代码:
class BinaryIndexedTree:def __init__(self, size):self.size = sizeself.tree = [0] * (size + 1)def _parent(self, index):while index > 1:index -= index & -indexreturn indexdef update(self, index, delta):while index <= self.size:self.tree[index] += deltaindex += self._parent(index)def query(self, index):result = 0while index > 0:result += self.tree[index]index -= self._parent(index)return result# 使用示例
bit = BinaryIndexedTree(10)
bit.update(1, 5) # 将索引1的值增加5
bit.update(3, 7) # 将索引3的值增加7print(bit.query(4)) # 查询索引1到4的和,应为12
在这个例子中,BinaryIndexedTree 类有三个方法:
__init__:初始化树状数组。update:在数组的指定索引位置增加一个值。query:查询从1到指定索引位置的累积和。
请注意,树状数组通常从索引1开始,而不是0,这与 Python 中列表的索引方式不同。如果你需要从0开始,可以在调用 update 和 query 方法时,将索引减1。
相关文章:

Python 树状数组
树状数组(Binary Indexed Tree, BIT),又称为斐波那契堆,是一种数据结构,用于高效地解决以下问题: 单点更新:在数组的某个位置增加或减少一个值。区间查询:查询数组中一段连续区间的…...
)
【QEMU中文手册】2.2 调用方式(持续更新中)
本文由 AI 翻译(ChatGPT-4)完成,并由作者进行人工校对。如有任何问题或建议,欢迎联系我。联系方式:jelin-shoutlook.com。 原文:Invocation — QEMU documentation qemu-system-x86_64 [选项] [磁盘镜像]磁…...
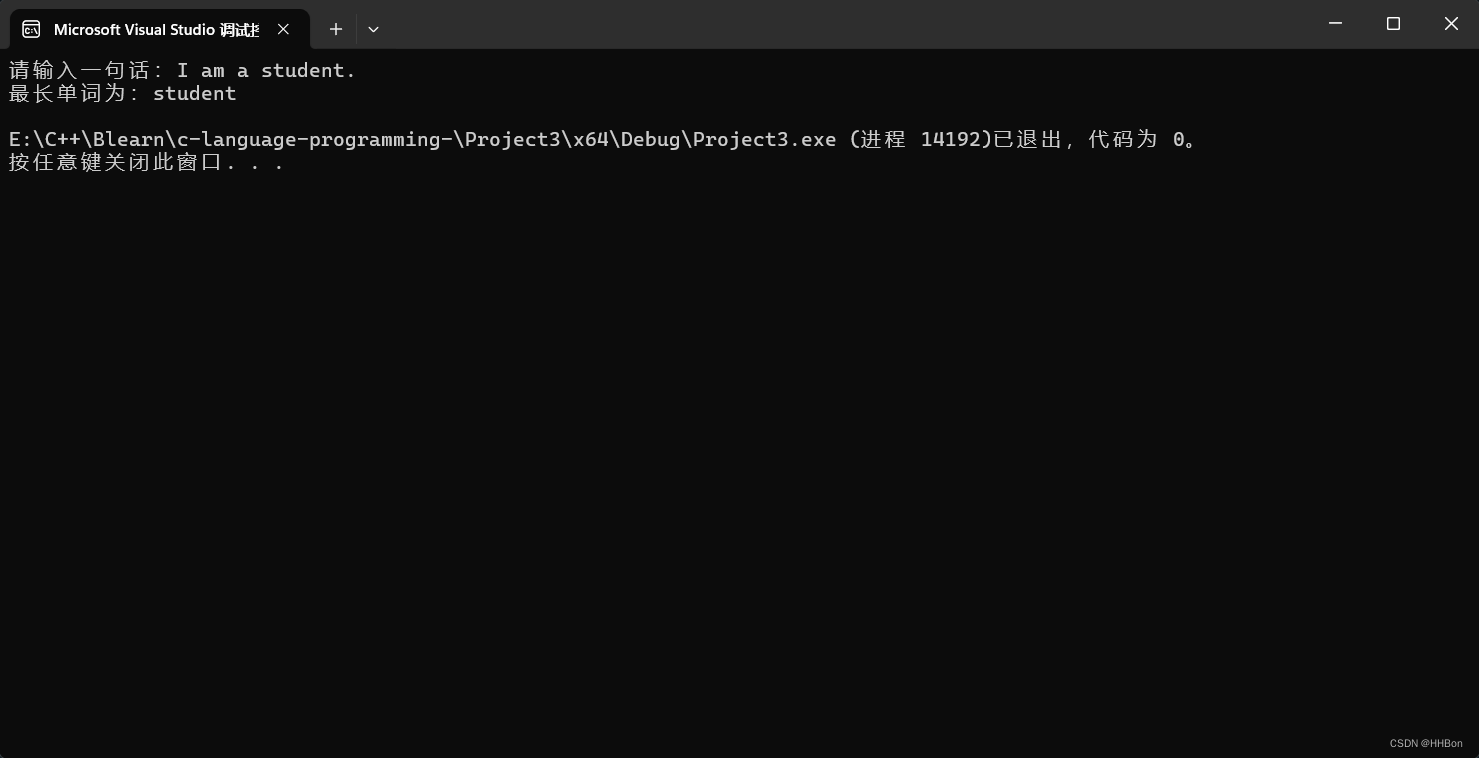
(函数)判断一句话中最长的单词(C语言)
一、运行结果; 二、源代码; # define _CRT_SECURE_NO_WARNINGS # include <stdio.h>//声明函数; int aiphabetic(char); int longest(char[]);int main() {//初始化变量值;int i;char line[100] { 0 };//获取用户输入字符…...

QT5.5.0中使用lambda表达式时遇到的问题
QT5.5中使用lambda表达式的遇到的error_qt中lamda不起作用-CSDN博客...

【Go语言精进之路】构建高效Go程序:了解切片实现原理并高效使用
🔥 个人主页:空白诗 文章目录 引言一、切片究竟是什么?1.1 基础的创建数组示例1.2 基础的创建切片示例1.3 切片与数组的关系 二、切片的高级特性:动态扩容2.1 使用 append 函数扩容2.2 容量管理与性能考量2.3 切片的截取与缩容 三…...

Python与C语言:深入探索两者的奥秘与差异
Python与C语言:深入探索两者的奥秘与差异 在编程的世界里,Python和C语言如同两位性格迥异的伙伴,各自拥有独特的魅力和应用场景。Python以其简洁易懂的语法和强大的库支持赢得了众多开发者的青睐,而C语言则以其接近硬件的低级特性…...

图像编解码器在AI绘画中的革新作用
随着人工智能技术的飞速发展,AI绘画已经从一个简单的概念演变为一个充满创意与可能性的领域。在这场技术与艺术的融合中,图像编解码器扮演着至关重要的角色。它们不仅提升了AI绘画的质量和效率,还拓宽了艺术创造的边界。本篇博客将深入探讨图…...

SecureCRT[po破] for Mac SSH终端操作工具[解] 安装教程
文章目录 效果一、准备工作二、开始安装1、双击运行软件,将其从左侧拖入右侧文件夹中,等待安装完毕2、 应用程序显示软件图标,表示安装成功 三、输入对应参数1、解决“软件已损坏,无法打开,要移到废纸篓”问题解决步骤…...

【大数据架构】基于流式数据的大数据架构升级
背景 团队在升级大数据架构,摒弃了原来基于hadoop的架构,因此抛弃了hive,hdfs,mapreduce这一套,在讨论和摸索中使用了新的架构。 后端使用kafka流式数据通过rest catalog写入iceberg,存储于minio。在写入iceberg的时候,首先是写data数据文件,然后再写iceberg的metada…...
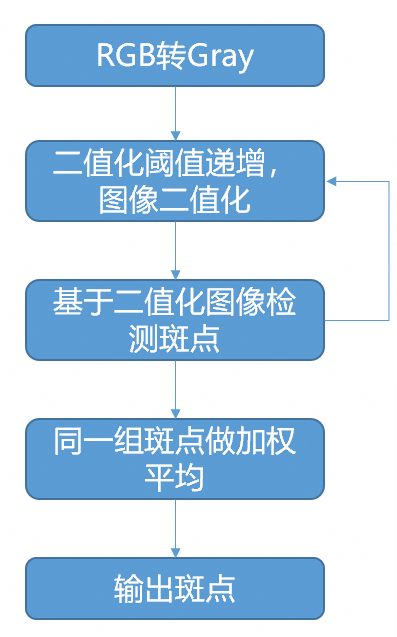
OpenCV中的圆形标靶检测——斑点检测算法(二)
前面的章节中我们已经大致介绍了算法流程,也对一些算法中用到的相关概念做了简要介绍,同时给出了算法调用的API,现在我们开始算法检测接口实现源码的分析。 1. 斑点的分组与加权 这里我们选择后者,先了解算法的处理流程,再分析各个模块的实现。算法流程图如下图所示,上一…...

网线制作(双绞线+水晶头)——T568B标准
参考视频:https://www.bilibili.com/video/BV1KQ4y1i7zP/ 1、使用剥线器 2、将线捋顺、排序、剪掉牵引线 记忆技巧 1.线序颜色整体是一浅一深 2.颜色顺序是黄、蓝、绿、棕 一个黄种人、从上向下看,分别看到的是蓝天、青草(绿)、泥土(棕色) 3.中间两根浅…...

湖南源点(市场研究咨询)如何产出更加有意义的竞品调研
湖南源点咨询认为:当前,任何项目都不能盲目开始,前期的准备工作必不可少。在基础架构搭建的同时,设计上对于前端功能、用户体验的调研就优先开始了。在这个阶段,大部分设计师都会分配很多调研任务,疯狂对竞…...

Qt/C++音视频开发76-获取本地有哪些摄像头名称/ffmpeg内置函数方式
一、前言 上一篇文章是写的用Qt的内置函数方式获取本地摄像头名称集合,但是有几个缺点,比如要求Qt5,或者至少要求安装了多媒体组件multimedia,如果没有安装呢,或者安装的是个空的呢,比如很多嵌入式板子&am…...

09 platfrom 设备驱动
platform 设备驱动,也叫做平台设备驱动。请各位重点学习! 1、驱动的分离与分层 1)驱动的分隔与分离 Linux 操作系统,代码的重用性非常重要。驱动程序占用了 Linux 内核代码量的大头,如果不对驱动程序加以管理,用不了多久 Linux 内核的文件数量就庞大到无法接受的地步。…...

【C#】C#读写Excel文件
1.工具库选择 使用EPPlus读取Excel文件,在visual studio2022中安装最新NuGet。 2.读文件测试 using OfficeOpenXml; using OfficeOpenXml.Packaging.Ionic.Zip; using OfficeOpenXml.Style; using System; using System.Collections.Generic; using System.IO; u…...
绘制规范)
数据流图(DFD)绘制规范
软件数据流图(Data Flow Diagram,DFD)是一种重要的工具,用于表示系统中数据的流动和处理。DFD帮助开发团队和利益相关者理解系统的功能和数据处理过程。绘制DFD时应遵循一定的规范和步骤,以确保图表的清晰性和一致性。…...
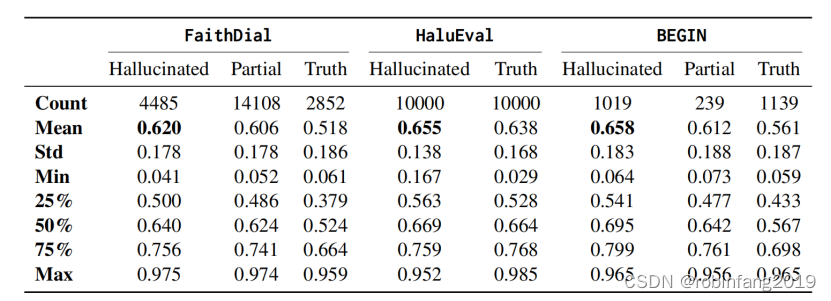
有待挖掘的金矿:大模型的幻觉之境
人工智能正在迅速变得无处不在,在科学和学术研究中,自回归的大型语言模型(LLM)走在了前列。自从LLM的概念被整合到自然语言处理(NLP)的讨论中以来,LLM中的幻觉现象一直被广泛视为一个显著的社会…...
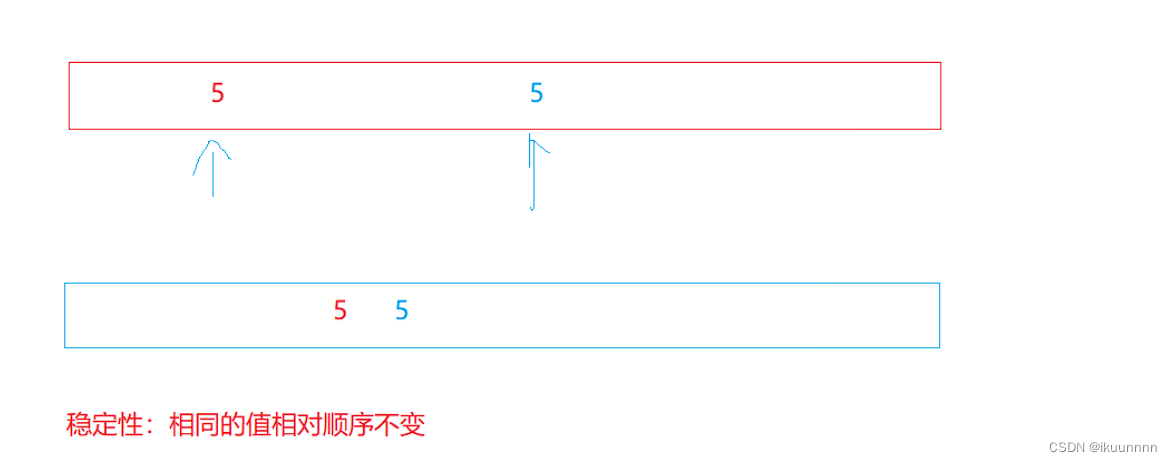
常见八大排序(纯C语言版)
目录 基本排序 一.冒泡排序 二.选择排序 三.插入排序 进阶排序(递归实现) 一.快排hoare排序 1.单趟排序 快排步凑 快排的优化 (1)三数取中 (2)小区间优化 二.前后指针法(递归实现) 三.快排的非…...
----vuex)
vue2学习(06)----vuex
目录 一、vuex概述 1.定义 优势: 2.构建环境步骤 3.state状态 4.使用数据 4.1通过store直接访问 4.2通过辅助函数 5.mutations修改数据(同步操作) 5.1定义 5.2步骤 5.2.1定义mutations对象,对象中存放修改state数据的方…...

webflux 拦截器验证token
在WebFlux中,我们可以使用拦截器(Interceptor)来验证Token。以下是一个简单的示例: 1. 首先,创建一个名为TokenInterceptor的类,实现HandlerInterceptor接口: java import org.springframewor…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
