【十大排序算法】快速排序

在乱序的世界中,快速排序如同一位智慧的园丁,
以轻盈的手法,将无序的花朵们重新安排,
在每一次比较中,沐浴着理性的阳光,
终使它们在有序的花园里,开出绚烂的芬芳。
文章目录
- 一、快速排序
- 二、发展历史
- 三、处理流程
- 四、算法实现
- 五、快速排序的特性
- 六、小结
- 推荐阅读
一、快速排序
快速排序是一种高效的排序算法,它采用了分治的策略。它的基本思想是选择一个基准值,将数组分为两个子数组,一个子数组中的所有元素都小于基准值,另一个子数组中的所有元素都大于基准值,然后对这两个子数组递归地进行排序。
具体来说,快速排序的步骤如下:
- 选择一个基准值(通常是数组的第一个元素、最后一个元素或者中间元素)。
- 将数组分为两个子数组,一个子数组中的所有元素都小于基准值,另一个子数组中的所有元素都大于基准值。
- 对这两个子数组递归地进行排序。
- 将排好序的子数组合并起来,即得到有序数组。
快速排序的关键在于分割操作,通过这个操作,它可以将一个大问题分解成两个规模较小的子问题,然后分别解决,最终达到整体有序的目的。
二、发展历史
快速排序是由英国计算机科学家 Tony Hoare 在 1960 1960 1960 年代提出的。Hoare 最初将这一算法称为 “分区交换排序”,后来更广泛地称为快速排序。他的灵感来自于合并排序和插入排序。
- 早期思想: Hoare 注意到合并排序在实践中性能良好,但需要额外内存空间;而插入排序则内存消耗较少,但在大规模数据下性能不佳。他希望能够结合两者的优点,创造出一种既能够节省空间又能够在平均情况下具有良好性能的排序算法。
- Hoare 分区法: Hoare 提出了一种称为 Hoare 分区法的分区策略,这成为了快速排序的核心部分。这个方法从数组中选择一个基准值,将数组分成两个部分,左边的部分包含比基准值小的元素,右边的部分包含比基准值大的元素。然后,递归地对这两个部分进行排序。
- 论文发表: Hoare 在 1961 1961 1961 年发表了关于快速排序的论文,论文中描述了这一算法的基本原理和实现方法。此后,他不断改进和优化这一算法,使得快速排序成为了一种非常高效的排序算法。
- 持续优化: 随着计算机科学的发展,许多学者对快速排序进行了进一步的优化和改进。例如,采用随机化的方式选择基准值,以防止最坏情况的发生;使用三数取中法来选择基准值,以提高算法的稳定性和性能等。
- 现代应用: 至今,快速排序仍然是一种非常流行和高效的排序算法,被广泛应用于各种编程语言和实际应用中。其简洁而优雅的设计理念以及优秀的性能使得它成为了排序算法中的经典之作。
三、处理流程
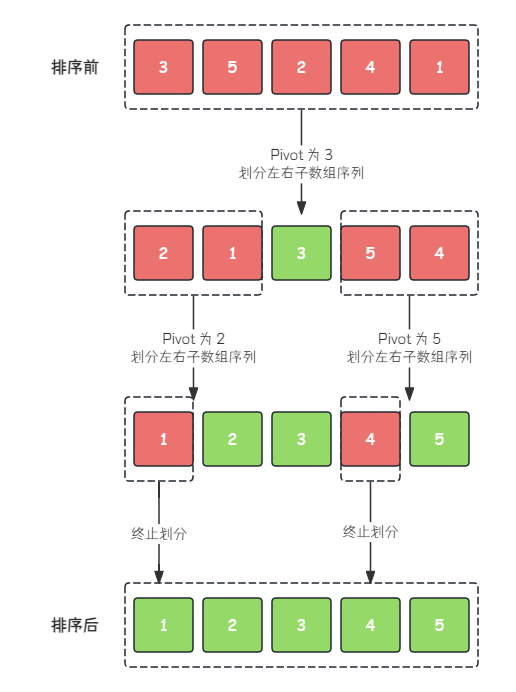
场景假设:我们需要将下列无序序列使用快速排序按从小到大进行排序。
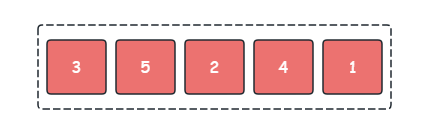
快速排序的流程如下:
- 在原序列中选取第一个元素 3 3 3 作为 Pivot 哨兵
- 将序列中小于 Pivot 的元素,放在 Pivot 的左边,大于 Pivot 的元素放在 Pivot 的右边
- 递归处理 Pivot 左边的序列和右边的序列
- 当子序列为长度 1 1 1 时终止
四、算法实现
// 快速排序入口
void quickSort(int[] arr, int low, int high) {if (low < high) {// 对数组进行分区操作int pivot = partition(arr, low, high);// 递归排序左半部分quickSort(arr, low, pivot - 1);// 递归排序右半部分quickSort(arr, pivot + 1, high);}
}// 分区操作
int partition(int[] arr, int low, int high) {// 选择最后一个元素作为 pivotint pivot = arr[high];int i = low - 1; // 指向小于 pivot 的区域的边界// 遍历数组,将小于 pivot 的元素放到左侧for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;// 交换元素int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}// 将 pivot 放到正确位置int temp = arr[i + 1];arr[i + 1] = arr[high];arr[high] = temp;// 返回 pivot的位置return i + 1;
}public static void main(String[] args) {int[] arr = {5, 3, 8, 6, 2, 7, 1, 4};// 调用快速排序算法quickSort(arr, 0, arr.length - 1);// 输出排序后的数组System.out.print("Sorted array: ");for (int num : arr) {System.out.print(num + " ");}
}
算法时间复杂度分析:
| 情况 | 时间复杂度 | 计算公式 | 公式解释 |
|---|---|---|---|
| 最好情况 | O ( n l o g n ) O(nlogn) O(nlogn) | T ( n ) = 2 T ( n 2 ) + n T(n) = 2T(\frac{n}{2}) + n T(n)=2T(2n)+n | 在最优情况下,每次划分都能将数组均匀地分成两部分。因此,我们有两个大小为 n 2 \frac{n}{2} 2n 的子问题,所以有 2 T ( n 2 ) 2T(\frac{n}{2}) 2T(2n)。然后,我们需要 n n n 的时间来进行划分操作。所以,总的时间复杂度就是 2 T ( n 2 ) + n 2T(\frac{n}{2}) + n 2T(2n)+n |
| 平均情况 | O ( n l o g n ) O(nlogn) O(nlogn) | T ( n ) = T ( n 2 ) + T ( n 2 ) + n T(n) = T(\frac{n}{2}) + T(\frac{n}{2}) + n T(n)=T(2n)+T(2n)+n | 在平均情况下,我们假设每次划分都能将数组均匀地分成两部分。因此,我们有两个大小为 n 2 \frac{n}{2} 2n 的子问题,所以有 T ( n 2 ) + T ( n 2 ) T(\frac{n}{2}) + T(\frac{n}{2}) T(2n)+T(2n)。然后,我们需要 n n n 的时间来进行划分操作。所以,总的时间复杂度就是 T ( n 2 ) + T ( n 2 ) + n T(\frac{n}{2}) + T(\frac{n}{2}) + n T(2n)+T(2n)+n |
| 最坏情况 | O ( n 2 ) O(n^2) O(n2) | T ( n ) = T ( n − 1 ) + n T(n) = T(n - 1) + n T(n)=T(n−1)+n | 在最坏情况下,每次划分只能将数组划分为一份有 n − 1 n - 1 n−1 个元素,另一份有 0 0 0 个元素。因此,我们有一个大小为 n − 1 n - 1 n−1 子问题,所以有 T ( n − 1 ) T(n - 1) T(n−1)。然后,我们需要 n n n 的时间来进行划分操作。所以,总的时间复杂度就是 T ( n − 1 ) + n T(n - 1) + n T(n−1)+n |
五、快速排序的特性
快速排序具有以下特性:
- 稳定性: 在一般情况下,快速排序是
不稳定的,即相同元素在排序后可能会改变相对位置。 - 原地性: 快速排序是一种原地排序算法,不需要额外的辅助空间,只需要使用原始数组进行排序。
- 适应性: 快速排序适用于各种数据类型,并且对部分有序的数据排序效果良好。
- 高效性: 快速排序在平均情况下具有 O ( n l o g n ) O(nlogn) O(nlogn) 的时间复杂度,使其成为处理大规模数据的理想选择。
六、小结
快速排序是一种非常重要且高效的排序算法,适用于各种数据类型和应用场景。其原地性、高效性以及简单直观的实现使得它成为了排序算法中的经典之作。
推荐阅读
- Spring 三级缓存
- 深入了解 MyBatis 插件:定制化你的持久层框架
- Zookeeper 注册中心:单机部署
- 【JavaScript】探索 JavaScript 中的解构赋值
- 深入理解 JavaScript 中的 Promise、async 和 await
相关文章:

【十大排序算法】快速排序
在乱序的世界中,快速排序如同一位智慧的园丁, 以轻盈的手法,将无序的花朵们重新安排, 在每一次比较中,沐浴着理性的阳光, 终使它们在有序的花园里,开出绚烂的芬芳。 文章目录 一、快速排序二、…...

linux系统ubuntu中在命令行中打开图形界面的文件夹
在命令行中打开当前路径,以文件管理器的形式打开: 命令 # 打开文件管理器 当前的路径 nautilus .nautilus 是一个与 GNOME 桌面环境集成的文件管理器的命令行启动程序。在 Linux 系统中,特别是使用 GNOME 作为桌面环境时,用户经…...
【C++11数据结构与算法】C++ 栈
C 栈(stack) 文章目录 C 栈(stack)栈的基本介绍栈的算法运用单调栈实战题LC例题:[321. 拼接最大数](https://leetcode.cn/problems/create-maximum-number/)LC例题:[316. 去除重复字母](https://leetcode.cn/problems/remove-duplicate-letters/) 栈的基…...
pdf文件如何防篡改内容
PDF文件防篡改内容的方法有多种,以下是一些常见且有效的方法,它们可以帮助确保PDF文件的完整性和真实性: 加密PDF文档: 原理:通过设置密码来保护PDF文档,防止未经授权的访问和修改。注意事项:密…...
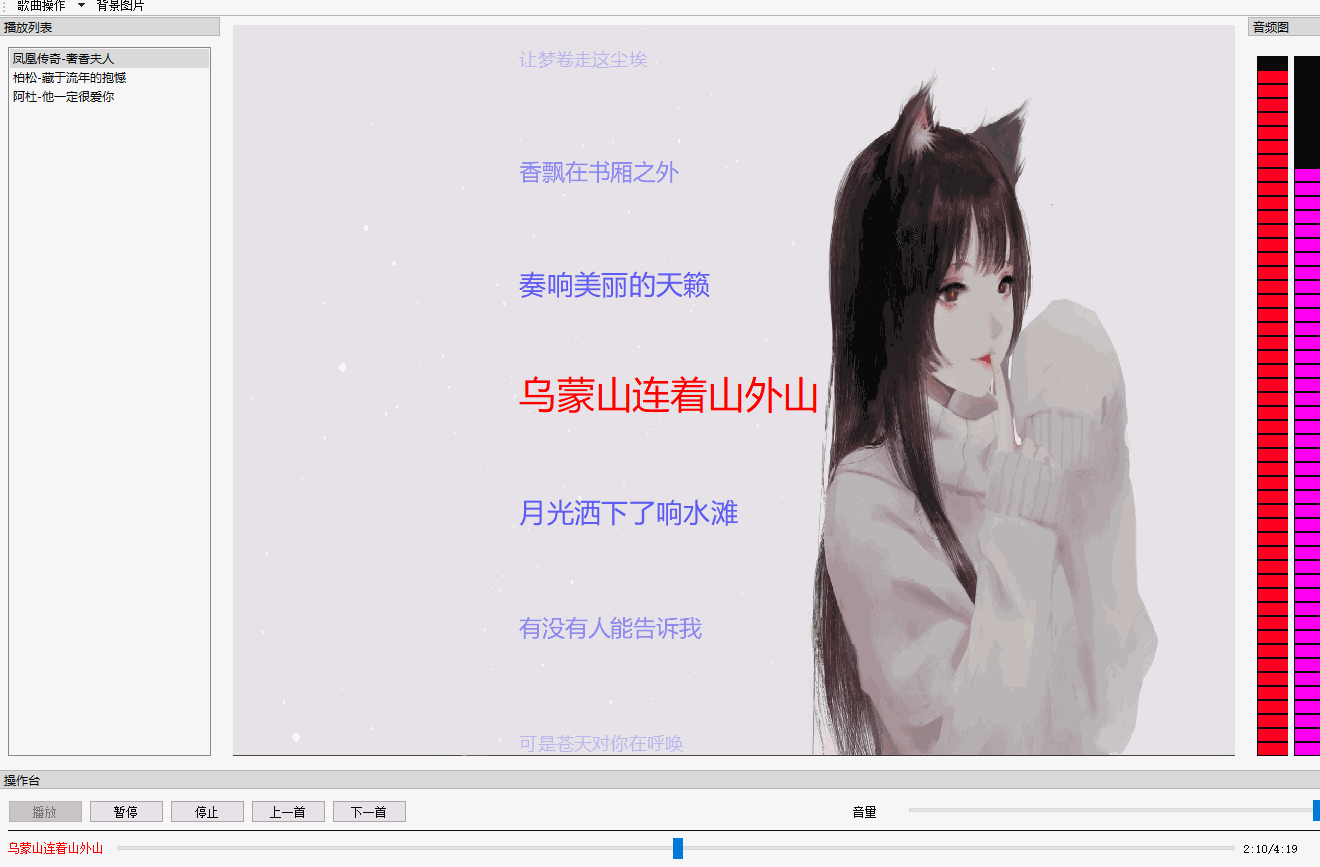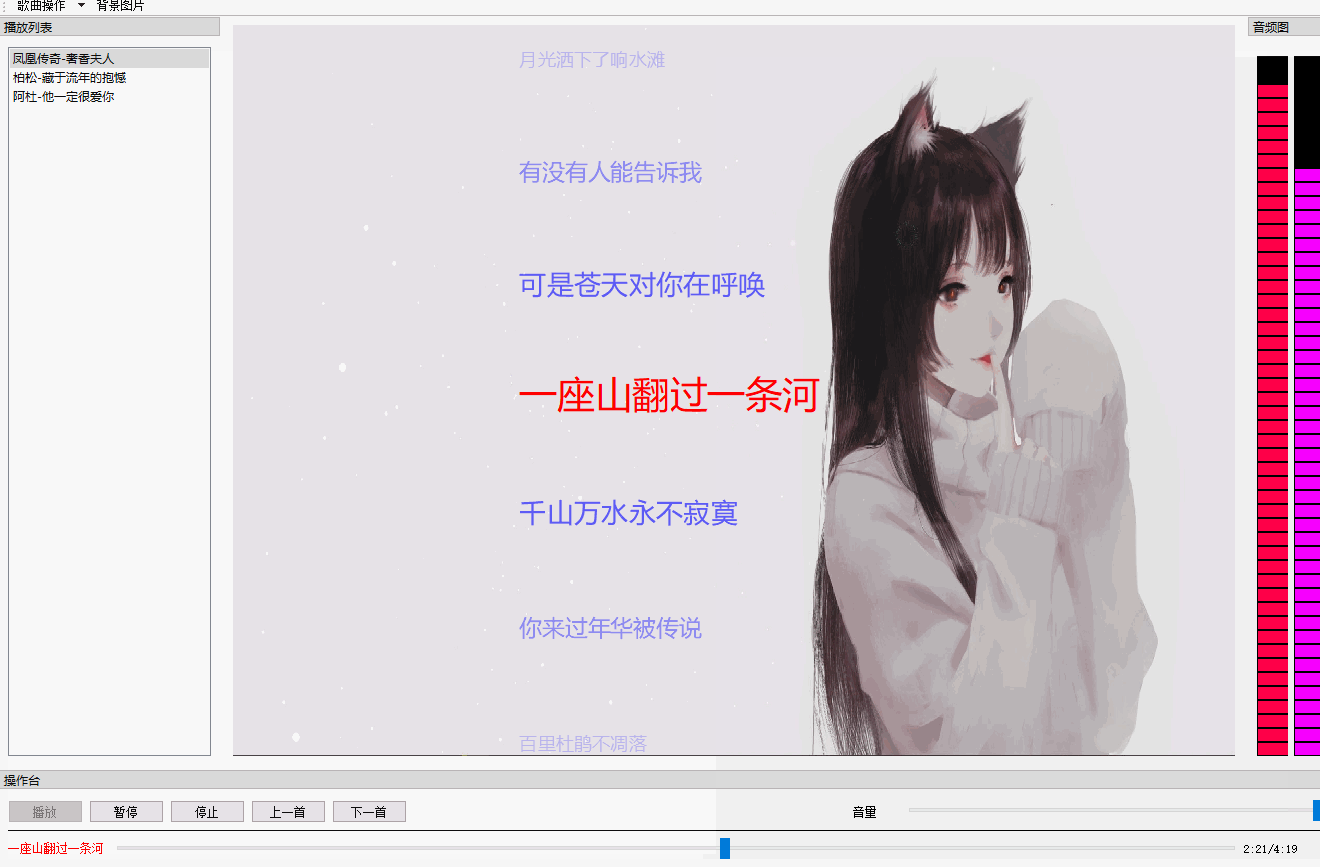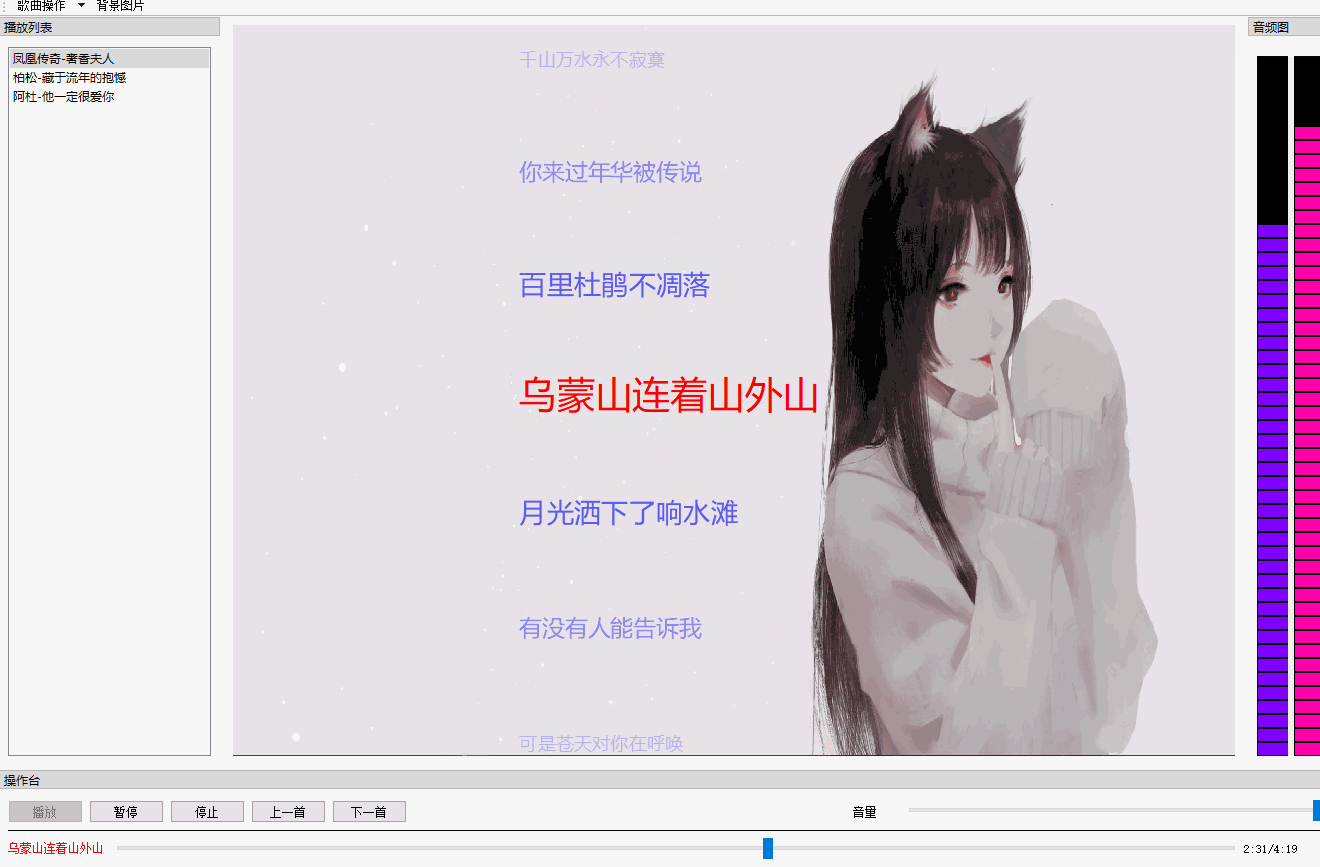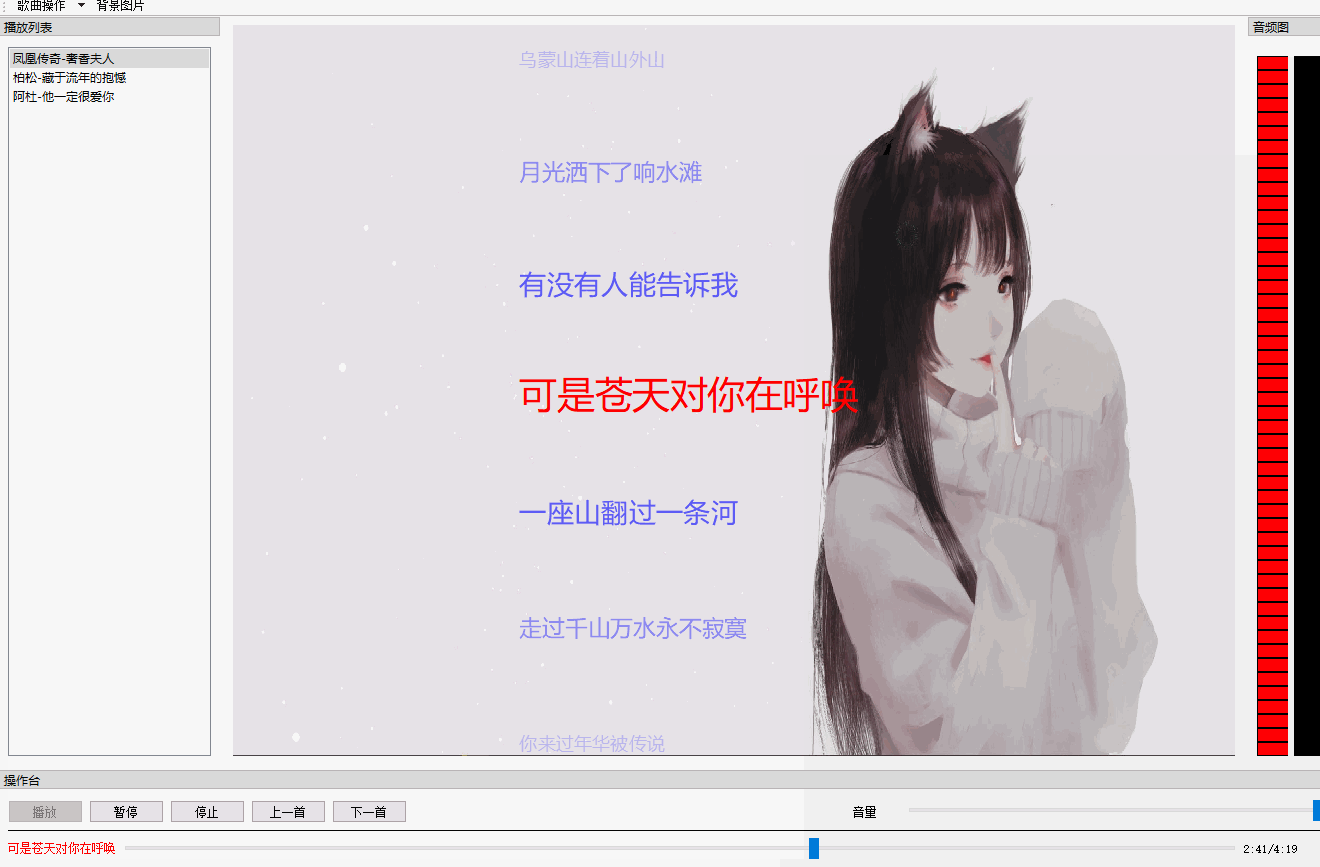
QT 音乐播放器【二】 歌词同步+滚动+特效
文章目录 效果图概述代码解析歌词歌词同步歌词特效 总结 效果图 概述 先整体说明一下这个效果的实现,你所看到的歌词都是QGraphicsObject,在QGraphicsView上绘制(paint)出来的。也就是说每一句歌词都是一个图元(item)。 为什么用QGraphicsView框架&…...
关于怎么用Cubemx生成的USBHID设备实现读取一体的鼠标键盘设备(改进版)
主要最近做了一个要用STM32实现读取鼠标键盘一体的那种USB设备,STM32的界面上要和电脑一样的能通过这个USB接口实现鼠标移动,键盘的按键。然后我就很自然的去参考了正点原子的例程,可是找了一圈,发现正点原子好像用的库函数&#…...
Soildworks学习笔记(二)
放样凸台基体: 自动生成连接两个物体两个面的基体: 2.旋转切除: 3.剪切实体: 4.转换实体引用: 将实体的轮廓线转换至当前草图使其成为当前草图的图元,主要用于在同一平面或另一个坐标中制作草图实体或其尺寸的副本。 …...

Linux配置uwsgi环境
Linux配置uwsgi环境 1.进入虚拟环境 source /envs/django_-shop-system/bin/activate2.安装uwsgi pip install uwsgi3.基于uwsgi运行项目 – 基于配置文件 在项目目录下创建配置文件 #socket 0.0.0.0:8005 http 0.0.0.0:8005 # http120.55.47.111:8005 chdir/opt/www/djang…...

Nagios的安装和使用
*实验* *nagios安装和使用* Nagios 是一个监视系统运行状态和网络信息的监视系统。Nagios 能监视所指定的本地或远程主机以及服务,同时提供异常通知功能等. Nagios 可运行在 Linux/Unix 平台之上,同时提供一个可选的基于浏览器的 WEB 界面以方便系统管…...
Numba 的 CUDA 示例(4/4):原子和互斥
本教程为 Numba CUDA 示例 第 4 部分。 本系列第 4 部分总结了使用 Python 从头开始学习 CUDA 编程的旅程 介绍 在本系列的前三部分(第 1 部分,第 2 部分,第 3 部分)中,我们介绍了 CUDA 开发的大部分基础知识…...

【机器学习】机器学习引领AI:重塑人类社会的新纪元
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀机器学习引领AI 📒1. 引言📕2. 人工智能(AI)🌈人工智能的发展🌞应用领…...

【制作面包game】
编写一个制作面包的游戏代码涉及到游戏设计、编程和用户界面设计等多个方面。这里我可以提供一个简化版本的Python代码示例,用于创建一个基本的面包制作游戏。这个游戏将会有一个简单的用户界面,玩家可以通过输入命令来制作面包。 游戏的基本流程如下&a…...

Django更改超级用户密码
Django更改超级用户密码 1、打开shell 在工程文件目录下敲入: python manage.py shell再在python交互界面输入: from django.contrib.auth.models import User user User.objects.get(username root) user.set_password(123456) user.save()其中ro…...

ROS基础学习-ROS通信机制进阶
ROS通信机制进阶 目录 0.简介1.常用API1.1 节点初始化函数1.1.1 C++1.1.2 Python1.2 话题与服务相关函数1.2.1 对象获取相关1.2.1.1 C++1.2.1.2 Python1.2.2 订阅对象相关1.2.2.1 C++1.2.2.2 Python1.2.3 服务对象相关函数1.2.3.1 C++1.2.3.2 Python1.2.4 客户端对象相关1.2.4.…...
 and shallowReadonly())
【Vue3】shallowReactive() and shallowReadonly()
历史小剧场 所谓历史,就是过去的事,它的残酷之处在于:无论你哀嚎,悲伤,痛苦,落寞,追悔,它都无法改变。 一具有名的尸体躺在无数无名的尸体上,这就是所谓的霸业。---- 《明…...
【javaEE初阶】
🌈🌈🌈关于java ⚡⚡⚡java的由来 我们这篇文章主要是来介绍javaEE,一般称为java企业版,实际上java的历史可以追溯到上个世纪90年代,当时主要的语言主流的还是C语言和C,但是在那个时期嵌入式初…...
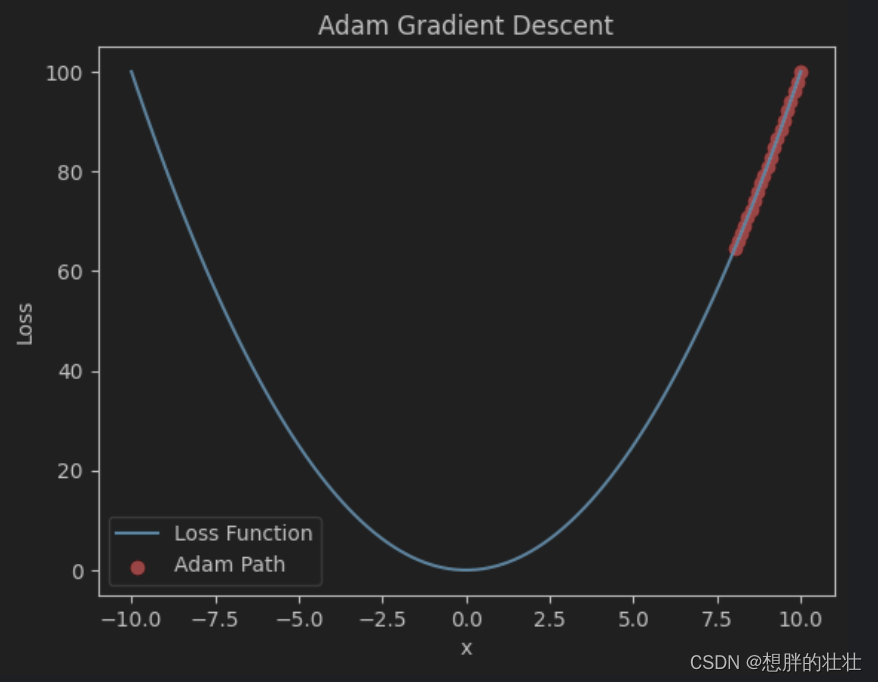
深度学习 - 梯度下降优化方法
梯度下降的基本概念 梯度下降(Gradient Descent)是一种用于优化机器学习模型参数的算法,其目的是最小化损失函数,从而提高模型的预测精度。梯度下降的核心思想是通过迭代地调整参数,沿着损失函数下降的方向前进&#…...
Steam下载游戏很慢?一个设置解决!
博主今天重装系统后,用steam下载发现巨慢 500MB,都要下载半小时。 平时下载软件,一般1分钟就搞定了,于是大致就知道,设置应该出问题了 于是修改了,如下设置之后,速度翻了10倍。 如下&#x…...

51单片机采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停
1、功能描述 采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停 2、实验原理 定时器原理:8051的定时器可以用于计数外部事件或执行内部定时操作。在本程序中,定时器1被设置为模式2,即8位自动重装载定时器模式…...

windows系统 flutter 开发环境配置
1、管理员运行powershell,安装:Chocolatey 工具,粘贴复制运行下列脚本: Chocolatey 官方安装文档 Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol [System.Net.ServicePointManage…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
