单调队列 加 二分
雾粉与最小值(简单版)
链接: 牛客
思路
题意是 给定我们数组a让我们完成{x,l,r}询问,判断是否在a中存在子数组满足长度在l,r之间且子数组最小值大于等于x,输出yes 或者 on
一个数组,长度越长,其最小值越小,所以询问只有最小长度是有用的,我们只需要判断是否存在子数组满足最小值大于等于x且长度大于询问的最小长度即可,所以我们的工作就是算出满足大于等于x的子数组的最大长度,显然暴力n^2的时间复杂度铁超时,这时候我们回想算一个子数组的最大长度,不就是找它左边第一个大于他的右边第一个大于他的数的区间嘛,单调队列,两趟O(n)拿下,然后我们获得了每个a[i]的扩展长度,也就是子数组的最小是a[i]的最大长度,这时候我们就像二分大于x的值判断长度是否大于询问的最小值了,可是这时候二分出来的第一个大于x的长度是满足大于等于x的最大长度吗?比如询问的x是5,我们二分出来的是7,7的长度是4,但是后面还有8的长度是9,是不是就错误了,所以我们要把8的长度9加到7的长度上,所以我们还需要给a[i]和他的扩展长度按照a[i]递减排序,然后累计最长长度加到每个a[i]身上,这样我们就确保了二分出来的就是最大长度,这里我们为了方便可以使用map进行二分操作。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, m;
struct node{int x, y;bool operator < (node & tem){if(x != tem.x)return x > tem.x;return y > tem.y;}
};
// 单调栈
int l[N], r[N], len[N];
int main()
{cin >> n;for(int i = 1; i <= n; i ++){cin >> a[i];}stack<int> st;// 找离a[i]最近的小于a[i]的最左位置//6 4 3 6维护一个单调减数列 1 3 2for(int i = 1; i <= n; i ++){while(st.size() && a[st.top()] >= a[i]){st.pop();}if(st.size()) l[i] = st.top()+1;else l[i] = 1;st.push(i);}// 找a[i] 右边最右的大于a[i]的元素stack<int> s;//1 2 3 8 2for(int i = n; i >= 1; i --){while(s.size() && a[s.top()] >= a[i]){s.pop();}if(s.size()) r[i] = s.top()-1;else r[i] = n;s.push(i);}vector<node> c;for(int i = 1; i <= n; i ++){len[i] = r[i] - l[i] + 1;c.push_back({a[i], len[i]});}sort(c.begin(), c.end());int maxlen = 0;map<int, int> cnt;for(int i = 0; i < c.size(); i ++){maxlen = max(maxlen, c[i].y);if(!cnt.count(c[i].x)) cnt[c[i].x] = maxlen;}cin >> m;for(int k = 1; k <= m; k ++){int x, ll, rr; cin >> x >> ll >> rr;auto res = cnt.lower_bound(x);if(res == cnt.end() || (res->second) < ll) cout << "No" << endl;else cout << "Yes" << endl;}return 0;
}
相关文章:

单调队列 加 二分
雾粉与最小值(简单版) 链接: 牛客 思路 题意是 给定我们数组a让我们完成{x,l,r}询问,判断是否在a中存在子数组满足长度在l,r之间且子数组最小值大于等于x,输出yes 或者 on 一个数组,长度越长,其最小值越小ÿ…...

Node.js 和 Vue 的区别的基本知识科普
Node.js和Vue.js在多个方面存在显著的区别。以下是这两者的主要区别,按照清晰的分点表示和归纳: Node.js 服务器端环境: Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它使JavaScript能够在服务器端运行。为JavaScript提供服务器端的环境服务,方便地搭建响应速度…...
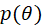
统计信号处理基础 习题解答10-10
题目 在本题中,我们讨论再生PDF。回顾前面 其中分母与无关。如果选择一个,使得它与相乘时,我们得到与相同形式的PDF,那么后验PDF 将有和相同的形式。例10.1的高斯PDF正是这样的一种情况。现在假设在条件下的的PDF是指数形式&…...

【蓝桥杯】C语言常见高级算法
🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 🍍博学而日参省乎己,知明而行无过矣 目录 🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 &a…...
FastJson
目录 FastJson 新建一个SpringBoot项目 pom.xml 一、JavaBean与JSON数据相互转换 LoginController FastJsonApplication启动类 编辑二、FastJson的JSONField注解 Log实体类 TestLog测试类 三、FastJson对JSON数据的增、删、改、查 TestCrud FastJson 1、JSON使用手册…...

Web3设计风格和APP设计风格
Web3设计风格和传统APP设计风格在视觉和交互设计上有一些显著的区别。这些差异主要源于Web3技术和理念的独特性,以及它们在用户体验和界面设计中的具体应用。以下是Web3设计风格与传统APP设计风格的主要区别。北京木奇移动技术有限公司,专业的软件外包开…...
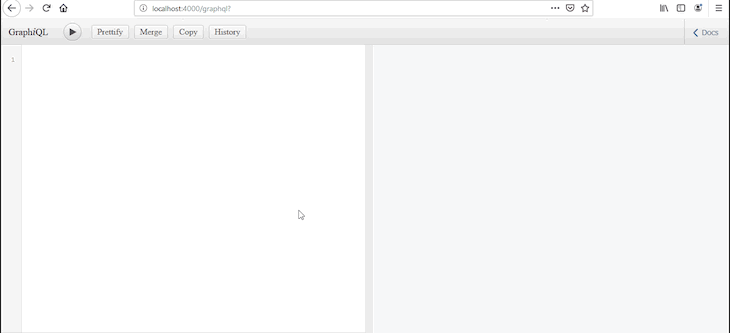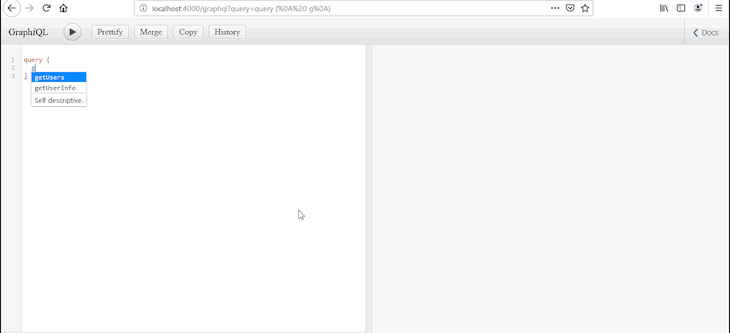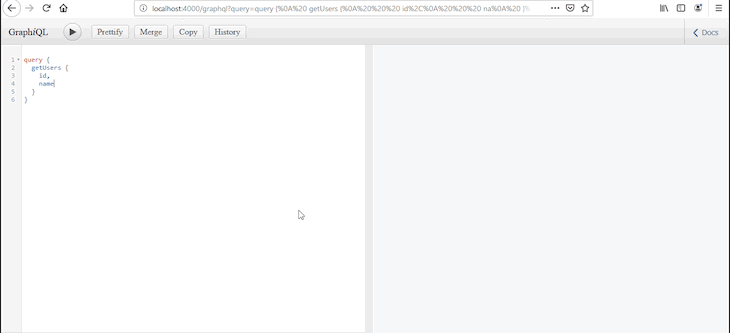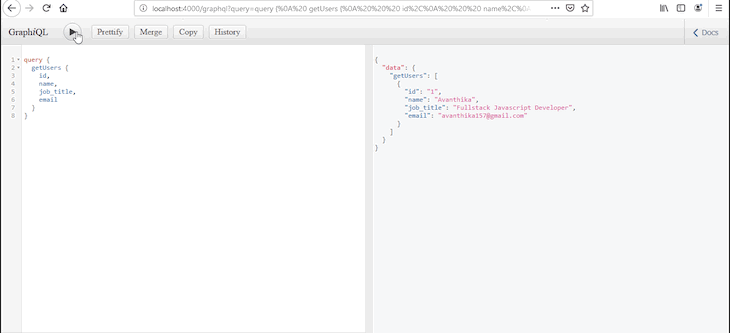
使用React和GraphQL进行CRUD:完整教程与示例
在本教程中,我们将向您展示如何使用GraphQL和React实现简单的端到端CRUD操作。我们将介绍使用React Hooks读取和修改数据的简单示例。我们还将演示如何使用Apollo Client实现身份验证、错误处理、缓存和乐观UI。 什么是React? React是一个用于构建用户…...

matplotlib 动态显示训练过程中的数据和模型的决策边界
文章目录 Github官网文档简介动态显示训练过程中的数据和模型的决策边界安装源码 Github https://github.com/matplotlib/matplotlib 官网 https://matplotlib.org/stable/ 文档 https://matplotlib.org/stable/api/index.html 简介 matplotlib 是 Python 中最常用的绘图…...

【学术小白成长之路】02三方演化博弈(基于复制动态方程)期望与复制动态方程
从本专栏开始,笔者正式研究演化博弈分析,其中涉及到双方演化博弈分析,三方演化博弈分析,复杂网络博弈分析等等。 先阅读了大量相关的博弈分析的文献,总结了现有的研究常用的研究流程,针对每个流程进行拆解。…...

短剧看剧系统投流版系统搭建,前端uni-app
目录 前言: 一、短剧看剧系统常规款短剧系统和投流版的区别? 二、后端体系 1.管理端: 2.代理投流端 三、功能区别 总结: 前言: 23年上半年共上新微短剧481部,相较于2022年全年上新的454部࿰…...

最新的ffmepg.js前端VUE3实现视频、音频裁剪上传功能
package.json "dependencies": {"ffmpeg/ffmpeg": "^0.12.10","ffmpeg/util": "^0.12.1" }vue3组件代码 根据需要更改 <script setup lang"ts"> import { FFmpeg } from ffmpeg/ffmpeg; import { fetchF…...

“Apache Kylin 实战指南:从安装到高级优化的全面教程
Apache Kylin是一个开源的分布式分析引擎,它提供了在Hadoop/Spark之上的SQL查询接口及多维分析(OLAP)能力,支持超大规模数据的亚秒级查询。以下是Kylin的入门教程,帮助您快速上手并使用这个强大的工具。 1. 安装Kylin Apache Kylin的安装是一个关键步骤,它要求您具备一…...

【iOS】内存泄漏检查及原因分析
目录 为什么要检测内存泄漏?什么是内存泄漏?内存泄漏排查方法1. 使用Zombie Objects2. 静态分析3. 动态分析方法定位修改Leaks界面分析Call Tree的四个选项: 内存泄漏原因分析1. Leaked Memory:应用程序未引用的、不能再次使用或释…...

“深入探讨Java中的对象拷贝:浅拷贝与深拷贝的差异与应用“
前言:在Java编程中,深拷贝(Deep Copy)与浅拷贝(Shallow Copy)是两个非常重要的概念。它们涉及到对象在内存中的复制方式,对于理解对象的引用、内存管理以及数据安全都至关重要。 ✨✨✨这里是秋…...

Docker 进入指定容器内部(以Mysql为例)
文章目录 一、启动容器二、查看容器是否启动三、进入容器内部 一、启动容器 这个就不多说了 直接docker run… 二、查看容器是否启动 查看正在运行的容器 docker ps查看所有的容器 docker ps -a结果如下图所示: 三、进入容器内部 通过CONTAINER ID进入到容器…...

计算机网络-数制转换与子网划分
目录 一、了解数制 1、计算机的数制 2、二进制 3、八进制 4、十进制 5、十六进制 二、数制转换 1、二进制转十进制 2、八进制转十进制 3、十六进制转十进制 4、十进制转二进制 5、十进制转八进制 6、十进制转十六进制 三、子网划分 1、IP地址定义 2、IP的两种协…...
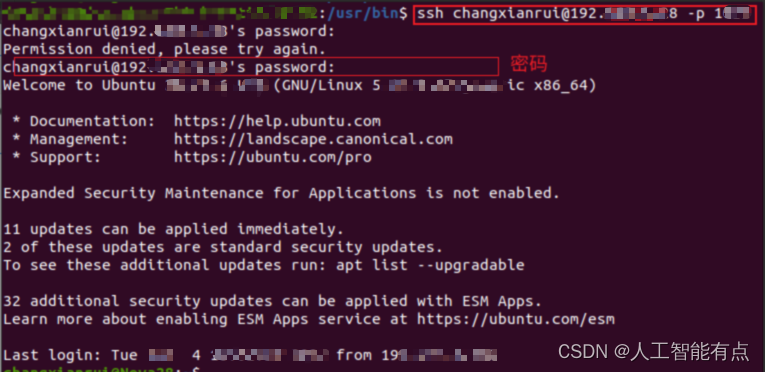
【ssh命令】ssh登录远程服务器
命令格式:ssh 用户名主机IP # 使用非默认端口: -p 端口号 ssh changxianrui192.168.100.100 -p 1022 # 使用默认端口 22 ssh changxianrui192.168.100.100 然后输入密码,就可以登录进去了。...
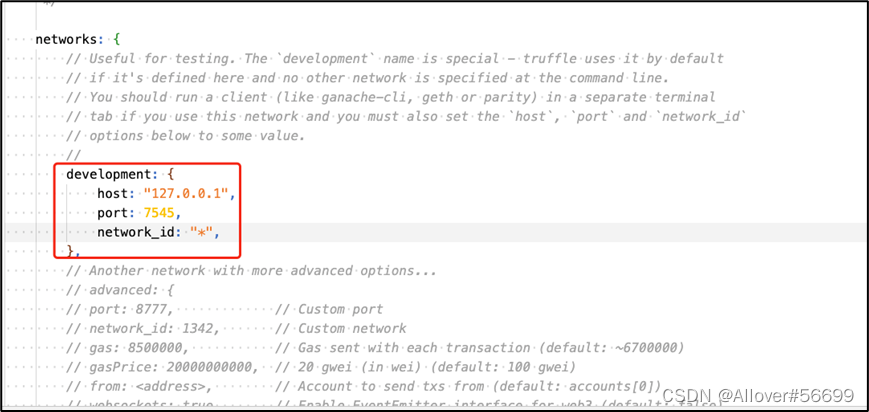
【区块链】truffle测试
配置区块链网络 启动Ganache软件 使用VScode打开项目的wordspace 配置对外访问的RPC接口为7545,配置项目的truffle-config.js实现与新建Workspace的连接。 创建项目 创建一个新的目录 mkdir MetaCoin cd MetaCoin下载metacoin盒子 truffle unbox metacoincontra…...

【AIGC调研系列】chatTTS与GPT-SoVITS的对比优劣势
ChatTTS和GPT-SoVITS都是在文本转语音(TTS)领域的重要开源项目,但它们各自有不同的优势和劣势。 ChatTTS 优点: 多语言支持:ChatTTS支持中英文,并且能够生成高质量、自然流畅的对话语音[4][10][13]。细粒…...

LLVM Cpu0 新后端10
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
