算法题day41(补5.27日卡:动态规划01)
一、动态规划基础知识:在动态规划中每一个状态一定是由上一个状态推导出来的。
动态规划五部曲:
1.确定dp数组 以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
debug方式:打印
二、刷题:
1.leetcode题目 509. 斐波那契数 - 力扣(LeetCode)(easy)
class Solution:def fib(self, n: int) -> int:if n<=1:return ndp = [0]*(n+1)dp[0] = 0dp[1] = 1for i in range(2,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]2.leetcode题目 70. 爬楼梯 - 力扣(LeetCode)(easy)
解决:
class Solution:def climbStairs(self, n: int) -> int:if n<=1:return ndp = [0]*3dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[2],dp[1] = dp[2] + dp[1],dp[2]return dp[2] 3.leetcode题目 746. 使用最小花费爬楼梯 - 力扣(LeetCode)
解决:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0] * (len(cost) + 1)dp[0] = 0dp[1] = 0for i in range(2,len(cost)+1):dp[i] = min(dp[i-1] + cost[i-1],dp[i-2]+cost[i-2])return dp[len(cost)]相关文章:
)
算法题day41(补5.27日卡:动态规划01)
一、动态规划基础知识:在动态规划中每一个状态一定是由上一个状态推导出来的。 动态规划五部曲: 1.确定dp数组 以及下标的含义 2.确定递推公式 3.dp数组如何初始化 4.确定遍历顺序 5.举例推导dp数组 debug方式:打印 二、刷题…...
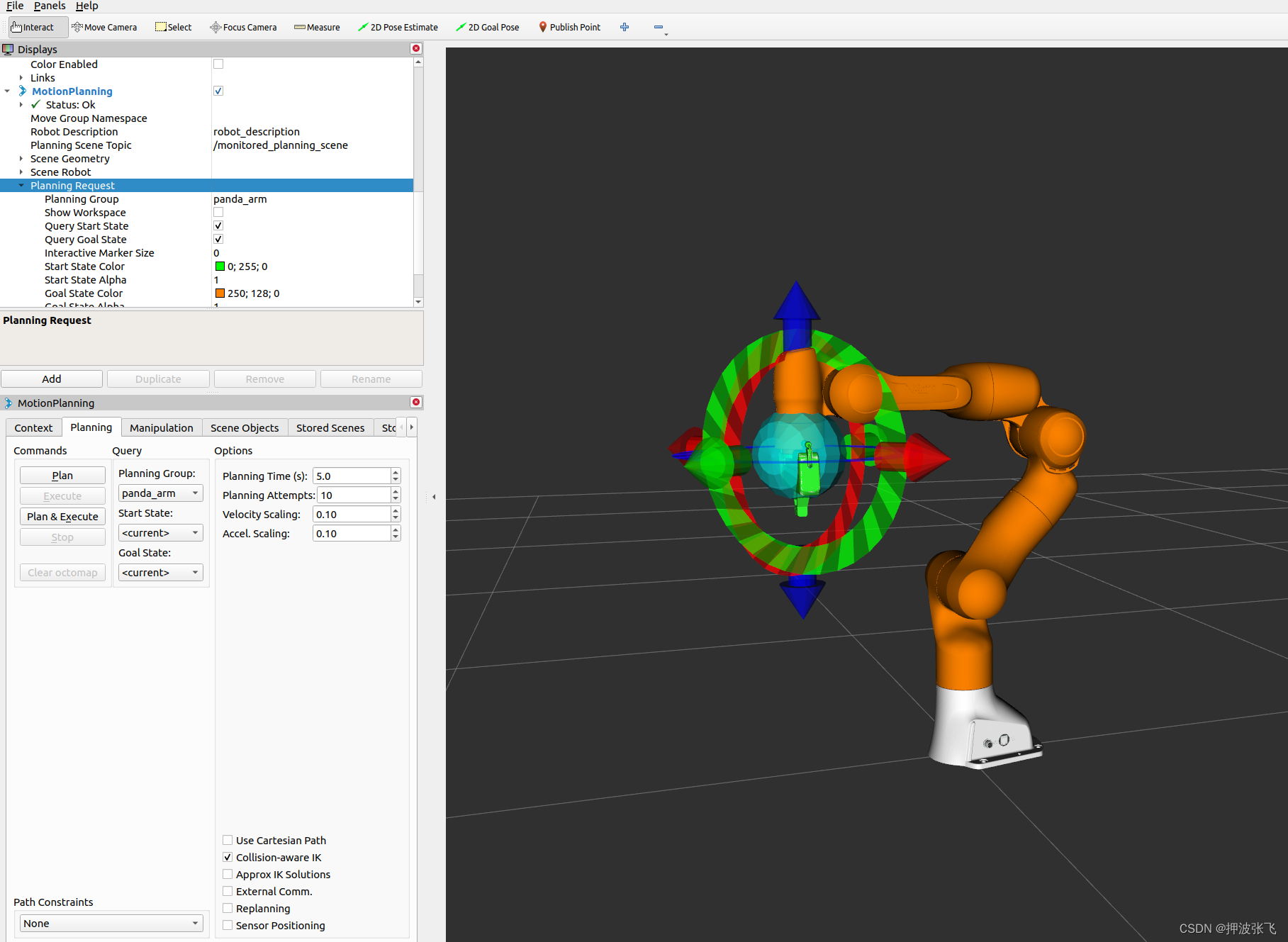
【附带源码】机械臂MoveIt2极简教程(四)、第一个入门demo
系列文章目录 【附带源码】机械臂MoveIt2极简教程(一)、moveit2安装 【附带源码】机械臂MoveIt2极简教程(二)、move_group交互 【附带源码】机械臂MoveIt2极简教程(三)、URDF/SRDF介绍 【附带源码】机械臂MoveIt2极简教程(四)、第一个入门demo 目录 系列文章目录1. 创…...
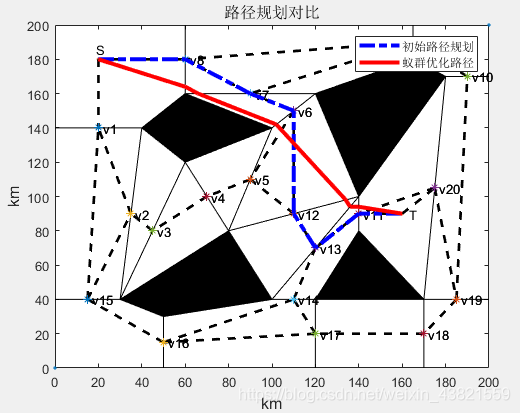
基于蚁群算法的二维路径规划算法(matlab)
微♥关注“电击小子程高兴的MATLAB小屋”获得资料 一、理论基础 1、路径规划算法 路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径。路径规划算法较多,大体上可分为全局路径规划算法和局部路径规划算法两大类。其…...
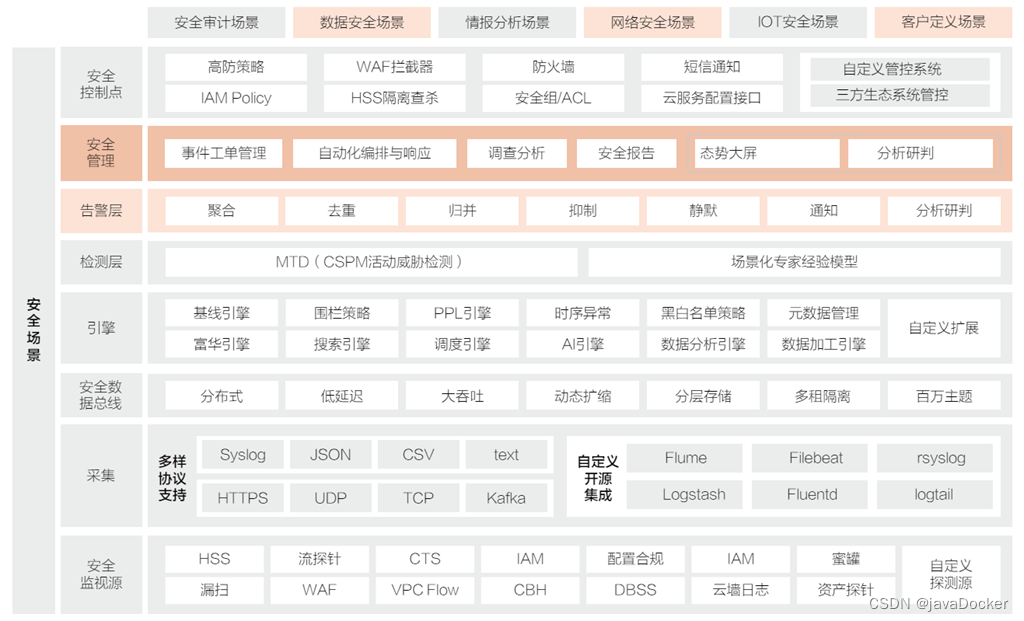
政务云参考技术架构
行业优势 总体架构 政务云平台技术框架图,由机房环境、基础设施层、支撑软件层及业务应用层组成,在运维、安全和运营体系的保障下,为政务云使用单位提供统一服务支撑。 功能架构 标准双区隔离 参照国家电子政务规范,打造符合标准的…...

android 13 aosp 预置so库
展讯对应的main.mk配置 device/sprd/qogirn**/ums***/product/***_native/main.mk $(call inherit-product-if-exists, vendor/***/build.mk)vendor/***/build.mk PRODUCT_PACKAGES \libtestvendor///Android.bp cc_prebuilt_library_shared{name:"libtest",srcs:…...

mongo篇---mongoDB Compass连接数据库
mongo篇—mongoDB Compass连接数据库 mongoDB笔记 – 第一条 一、mongoDB Compass连接远程数据库,配置URL。 URL: mongodb://username:passwordhost:port点击connect即可。 注意:host最好使用名称,防止出错连接超时。...

基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真,输出收敛曲线以及三维曲面最高点搜索结果。 2.测试软件版本以及运行结果展示 MATLAB2022A版本…...

前端js解析websocket推送的gzip压缩json的Blob数据
主要依赖插件pako https://www.npmjs.com/package/pako 1、安装 npm install pako 2、使用, pako.inflate(reader.result, {to: "string"}) 解压后的string 对象,需要JSON.parse转成json this.ws.onmessage (evt) > {console.log("…...
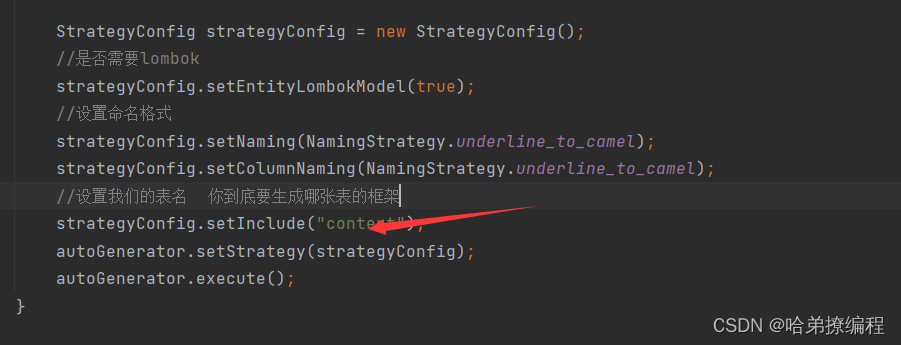
【wiki知识库】06.文档管理接口的实现--SpringBoot后端部分
目录 一、🔥今日目标 二、🎈SpringBoot部分类的添加 1.调用MybatisGenerator 2.添加DocSaveParam 3.添加DocQueryVo 三、🚆后端新增接口 3.1添加DocController 3.1.1 /all/{ebokId} 3.1.2 /doc/save 3.1.3 /doc/delete/{idStr} …...

c,c++,go语言字符串的演进
#include <stdio.h> #include <string.h> int main() {char str[] {a,b,c,\0,d,d,d};printf("string:[%s], len:%d \n", str, strlen(str) );return 0; } string:[abc], len:3 c语言只有数组的概念,数组本身没有长度的概念,需…...
vue-cli 快速入门
vue-cli (目前向Vite发展) 介绍:Vue-cli 是Vue官方提供一个脚手架,用于快速生成一个Vue的项目模板。 Vue-cli提供了如下功能: 统一的目录结构 本地调试 热部署 单元测试 集成打包上线 依赖环境:NodeJ…...

机器人--矩阵运算
两个矩阵相乘的含义 P点在坐标系B中的坐标系PB,需要乘以B到A到变换矩阵TAB。 M点在B坐标系中的位姿MB,怎么计算M在A中的坐标系? 两个矩阵相乘 一个矩阵*另一个矩阵的逆矩阵...

期末复习【汇总】
期末复习【汇总】 前言版权推荐期末复习【汇总】最后 前言 2024-5-12 20:52:17 截止到今天,所有期末复习的汇总 以下内容源自《【创作模板】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此话 本文首次发布于CSDN平台 作者是CSDN日星月云 博客主页是ht…...
- CONNACK Packet)
【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet
【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet 文章目录 【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet前言说明一、固定同步详解、可变头部详解总结 前言 关于所有的类型的数据示例已经在上面一篇博客说完: …...

Linux - 深入理解/proc虚拟文件系统:从基础到高级
文章目录 Linux /proc虚拟文件系统/proc/self使用 /proc/self 的优势/proc/self 的使用案例案例1:获取当前进程的状态信息案例2:获取当前进程的命令行参数案例3:获取当前进程的内存映射案例4:获取当前进程的文件描述符 /proc中进程…...
Django DeleteView视图
Django 的 DeleteView 是一个基于类的视图,用于处理对象的删除操作。 1,添加视图函数 Test/app3/views.py from django.shortcuts import render# Create your views here. from .models import Bookfrom django.views.generic import ListView class B…...

代码杂谈 之 pyspark如何做相似度计算
在 PySpark 中,计算 DataFrame 两列向量的差可以通过使用 UDF(用户自定义函数)和 Vector 类型完成。这里有一个示例,展示了如何使用 PySpark 的 pyspark.ml.linalg.Vectorspyspark.sql.functions.udf 来实现这一功能:…...
混剪素材哪里找?分享8个热门素材网站
今天我们来深入探讨如何获取高质量的混剪素材,为您的短视频和自媒体制作提供最佳资源。在这篇指南中,我将介绍几个热门的素材网站,让您轻松掌握素材获取的技巧,并根据百度SEO排名规则,优化关键词的使用,确保…...

临床应用的深度学习在视网膜疾病的诊断和转诊中的应用| 文献速递-视觉通用模型与疾病诊断
Title 题目 Clinically applicable deep learning for diagnosis and referral in retinal disease 临床应用的深度学习在视网膜疾病的诊断和转诊中的应用 01 文献速递介绍 诊断成像的数量和复杂性正在以比人类专家可用性更快的速度增加。人工智能在分类一些常见疾病的二…...

中继器简介
一、网络信号衰减问题 现在的网路信号有两种,一种是电信号,另一种的光信号,电信号在网线、电话线或者电视闭路线中传输,光信号在光缆中传输,但是不管是以那种信号进行传输,随着传输距离的增加,电…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
