当前位置： 首页 > news >正文

docker容器部署jenkins

news 2026/2/9 12:56:17

提前安装好jdk和maven，jdk最好使用11版本，jdk-11.0.10

docker run -u root -d \
-p 100:8080 \
-v /var/jenkins_home/workspace/:/var/jenkins_home/workspace/ \
-v /var/run/docker.sock:/var/run/docker.sock \
-v /usr/bin/docker:/usr/bin/docker \
-v /usr/local/java/jdk1.8.0_241:/usr/local/java \
-v /usr/local/apache-maven-3.9.1:/usr/local/maven \
-e JAVA_OPTS="-Dorg.apache.commons.jelly.tags.fmt.timeZone='Asia/Shanghai" \
--name myjenkins jenkins/jenkins:2.401

参考：

使用Docker安装部署Jenkins_docker部署jenkins-CSDN博客

流水线编写示例：Jenkins把GitHub项目做成Docker镜像_ITPUB博客 

相关文章：

docker容器部署jenkins

提前安装好jdk和maven，jdk最好使用11版本，jdk-11.0.10 docker run -u root -d \ -p 100:8080 \ -v /var/jenkins_home/workspace/:/var/jenkins_home/workspace/ \ -v /var/run/docker.sock:/var/run/docker.sock \ -v /usr/bin/docker:/usr/bin/docker…...

编程日记 2024/6/12 13:30:12

第十四章 享元模式

目录 1 享元模式介绍 2 享元模式原理 3 享元模式实现 4 享元模式应用实例 5 享元模式总结 1 享元模式介绍 享元模式 (flyweight pattern) 的原始定义是：摒弃了在每个对象中保存所有数据的方式，通过共享多个对象所共有的相同状态，从而让我…...

编程日记 2024/6/12 13:29:11

ThinkBook 16 2024 Ubuntu 触控板问题解决

sudo insmod goodix-gt7868q.ko sudo cp local-overrides.quirks /etc/libinput/local-overrides.quirks sudo systemctl restart gdm 有偿解决，无效退款...

编程日记 2024/6/12 13:27:09

qt qDebug兼容LOGE

目录 普通qDebug用法 qt qDebug兼容LOGE 模板参数2实现 qDebug 实现LOGE一样的用法，这样Android和qt同时支持LOGE打印日志 普通qDebug用法 #include <QApplication> #include <QDebug>int main(int argc, char *argv[]) {QApplication app(argc, argv);int ret…...

编程日记 2024/6/12 13:26:08

【Ardiuno】实验使用ESP32单片机连接Wifi（图文）

ESP32单片机最为精华和有特色的地方当然是wifi连接&#xff0c;这里我们就写程序实验一下适使用ESP32主板连接wifi&#xff0c;为了简化实验我们这里只做了连接部分&#xff0c;其他实验在后续再继续。 由于本实验只要在串口监视器中查看结果状态即可&#xff0c;因此电路板上…...

编程日记 2024/6/12 13:25:07

常用的五大数据可视化工具测评分享

随着数据驱动决策的时代到来&#xff0c;数据可视化工具成为了企业提升数据分析效率和决策质量的关键工具。本文将对帆软BI、奥威BI、思迈特BI、永洪BI以及亿信华辰BI这五大数据可视化工具进行详细的操作体验测评&#xff0c;总结它们的特点和优势。 一、帆软BI 帆软BI作为国…...

编程日记 2024/6/12 13:24:06

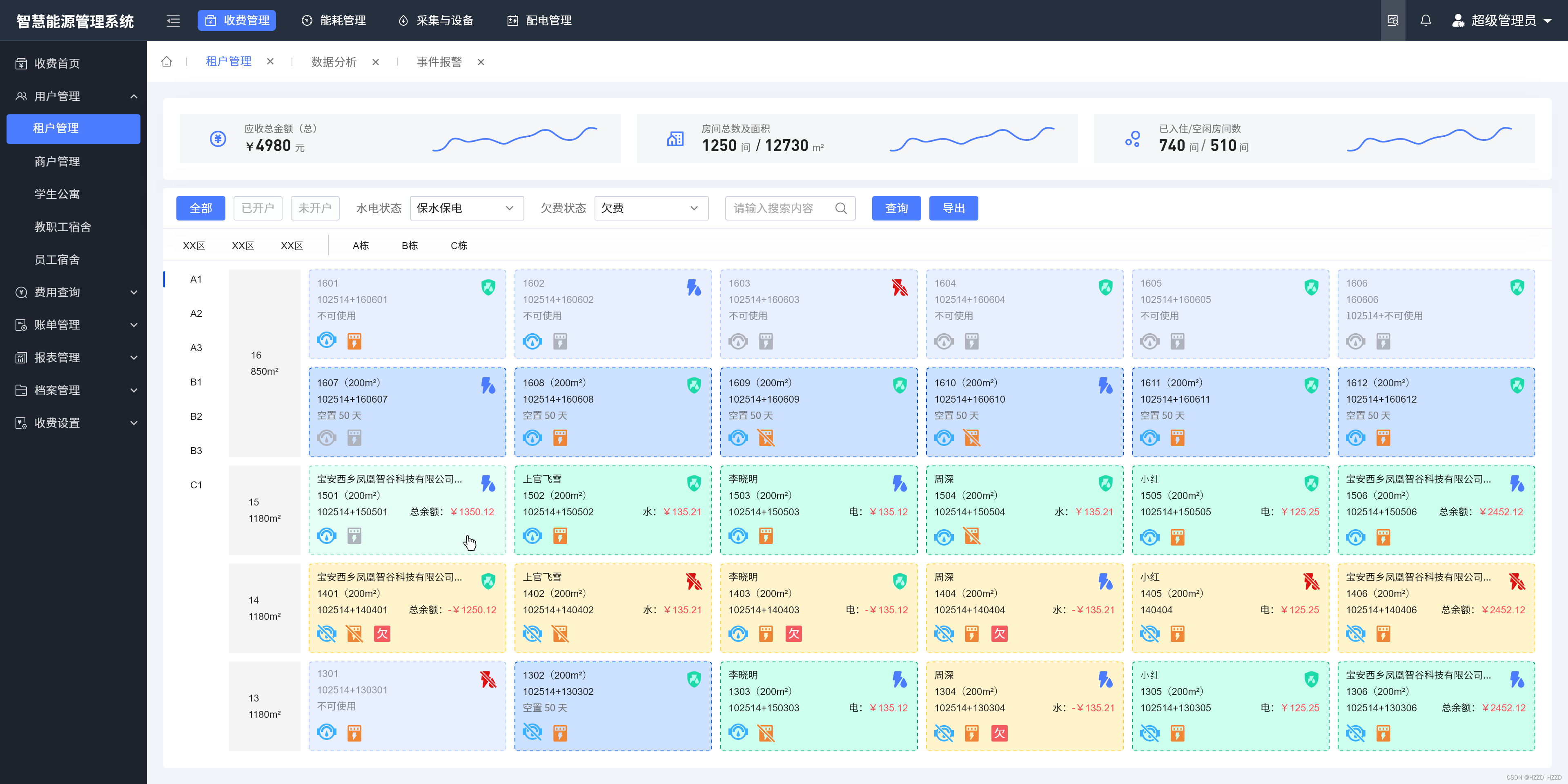
什么是校园抄表系统？

1.校园抄表系统的简述 校园抄表系统是当代高校管理中的一个重要组成部分&#xff0c;主要运用于全自动搜集、管理方法与分析校园里的电力能源使用数据&#xff0c;如水电煤等。它通过先进的方式方法&#xff0c;完成了对能源消耗的实时监控系统&#xff0c;提升了电力能源管理…...

编程日记 2024/6/12 13:23:05

计算机专业：未来何去何从？

💝💝💝欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 jav…...

编程日记 2024/6/12 13:21:02

python-windows10普通笔记本跑bert mrpc数据样例0.1.048

python-windows10普通笔记本跑bert mrpc数据样例0.1.000 背景参考章节获取数据下载bert模型下载bert代码windows10的cpu进行训练进行预测注意事项TODOLIST背景 看了介绍说可以在gpu或者tpu上去微调，当前没环境，所以先在windows10上跑一跑，看是否能顺利进行，目标就是训练的…...

编程日记 2024/6/12 13:20:01

4句话明白虚拟机和容器的区别

一、虚拟机VM的组成 服务器-HostOS-虚拟化层-GustOS-libs-App 1、此时存在几个问题&#xff1a; 1、资源消耗大 2、扩展APP副本时到重复资源浪费&#xff08;GustOS-libs&#xff09; 3、当你开发在本地但要移植到云端&#xff0c;就会出现各种兼容性问题。 4、很难集成到DevOp…...

编程日记 2024/6/12 13:16:57

Django render()函数页面渲染

1&#xff0c; render() 函数 在Django框架中&#xff0c;render() 函数是一个非常有用的快捷方式&#xff0c;用于从视图函数返回一个完整的HTTP响应。它负责将给定的模板与上下文数据结合&#xff0c;渲染出最终的HTML页面&#xff0c;并返回一个HttpResponse对象。 from d…...

编程日记 2024/6/12 13:15:56

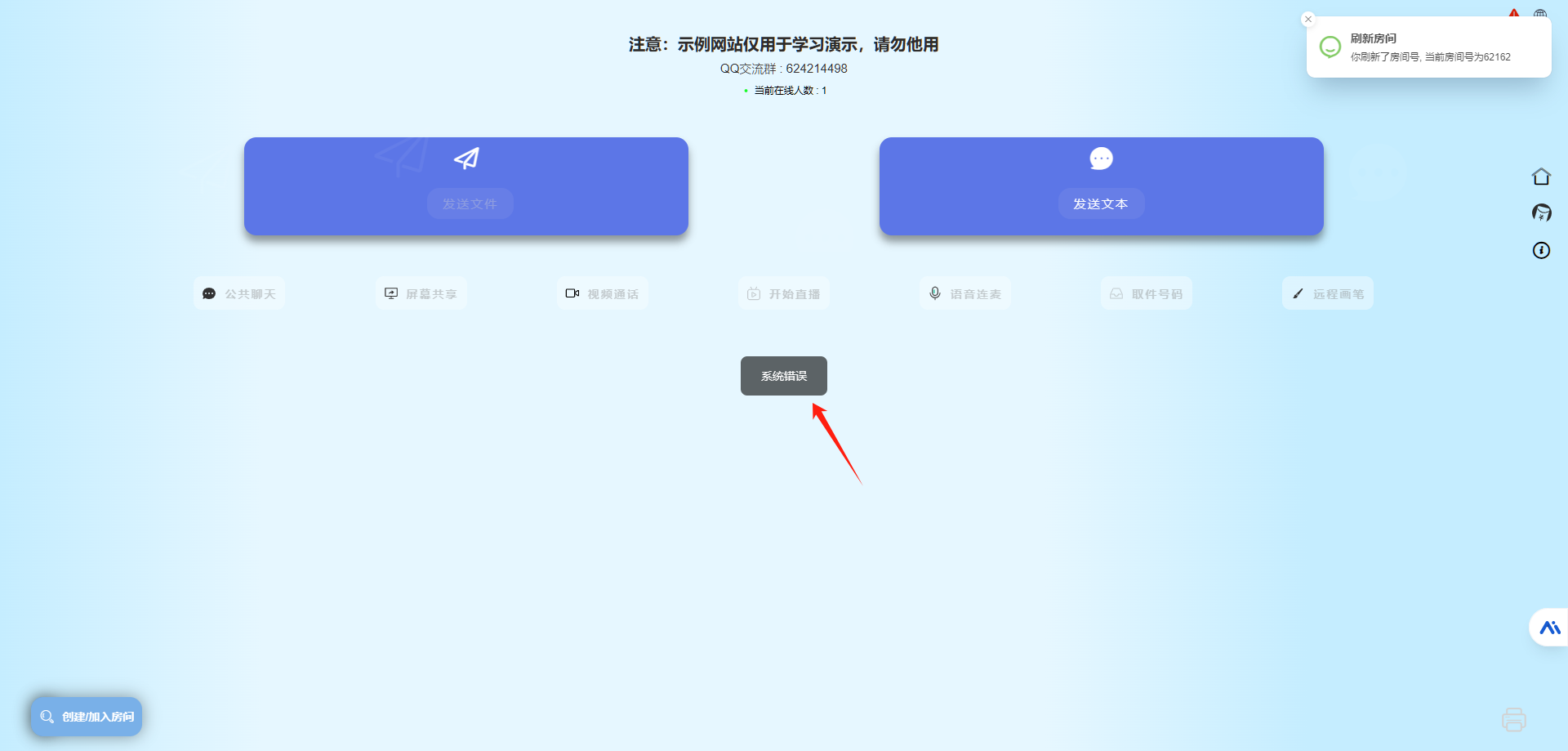
基于webrtc的媒体流传输工具tl-rtc-file

也不知道是什么意思&#xff0c;天天都有人在微信公众号的后台发&#xff0c;是打算找我兑奖吗&#xff1f; 本文软件是朋友 Eduna 推荐的&#xff0c;因为他觉得好像很好玩的样子。老苏一开始以为 tl-rtc-file 是跟 Snapdrop 一样的局域网文件传输工具&#xff0c;在看了 demo…...

编程日记 2024/6/12 13:13:53

【最新鸿蒙应用开发】——类Web开发范式2——前端语法

兼容JS的类Web开发范式 JS FA应用的JS模块(entry/src/main/js/module)的典型开发目录结构如下&#xff1a; 1. 项目基本结构 1.1. 目录结构 1.2. 项目文件分类如下&#xff1a; .hml结尾的HML模板文件&#xff0c;这个文件用来描述当前页面的文件布局结构。 .css结尾的CSS样…...

编程日记 2024/6/12 13:12:52

前端的强缓存和协商缓存

前端缓存机制 前端缓存主要分为两种类型&#xff1a;强缓存和协商缓存。 强缓存&#xff08;HTTP Cache-Control&#xff09; 通过设置HTTP响应头中的Cache-Control实现。浏览器根据Cache-Control的值决定是否重新请求资源。指令示例&#xff1a; no-cache&#xff1a;重新验…...

编程日记 2024/6/12 13:11:51

JSON如何处理包含特殊字符的字段

在JSON中处理包含特殊字符的字段时&#xff0c;你通常不需要直接处理这些特殊字符&#xff0c;因为JSON格式本身就会对特殊字符进行转义。当你使用编程语言或工具来生成或解析JSON时&#xff0c;这些转义通常是自动处理的。 然而&#xff0c;如果你需要手动处理或理解这些转义…...

编程日记 2024/6/12 13:10:49

JavaScript 中的 AbortController

AbortController 接口是 JavaScript 中 Fetch API 的一部分&#xff0c;引入它是为了处理和控制中止 fetch 请求的信号。这在需要取消正在进行的网络请求时特别有用&#xff0c;例如用户发起的动作取消&#xff0c;通过避免不必要的请求来提高性能&#xff0c;或优雅地处理超时…...

编程日记 2024/6/12 13:09:48

【前端】vue在线编辑器

以下是几个推荐的在线编辑器&#xff1a; CodeSandbox URL: https://codesandbox.io/特点: 支持 Vue、React、Angular 等多种前端框架&#xff0c;功能强大&#xff0c;社区活跃。 JSFiddle URL: https://jsfiddle.net/特点: 轻量级的在线编辑器&#xff0c;支持 Vue&#xff…...

编程日记 2024/6/12 13:08:47

leetcode67：二进制求和

题目链接&#xff1a;67. 二进制求和 - 力扣&#xff08;LeetCode&#xff09; class Solution { public:string addBinary(string a, string b) {int stralen a.size(), strblen b.size();int curtc;int Maxlen max(stralen, strblen);vector<int> stra;vector<i…...

编程日记 2024/6/12 13:07:46

程序员必备的职业素养：专业精神、沟通能力与持续学习

&#x1f34e;个人博客&#xff1a;个人主页 &#x1f3c6;个人专栏&#xff1a;日常聊聊 ⛳️ 功不唐捐&#xff0c;玉汝于成 目录 前言 正文 专业精神&#xff1a;技术的执着追求 沟通能力&#xff1a;团队合作的桥梁 持续学习&#xff1a;不断进步的动力 结语 我的…...

编程日记 2024/6/12 13:06:44

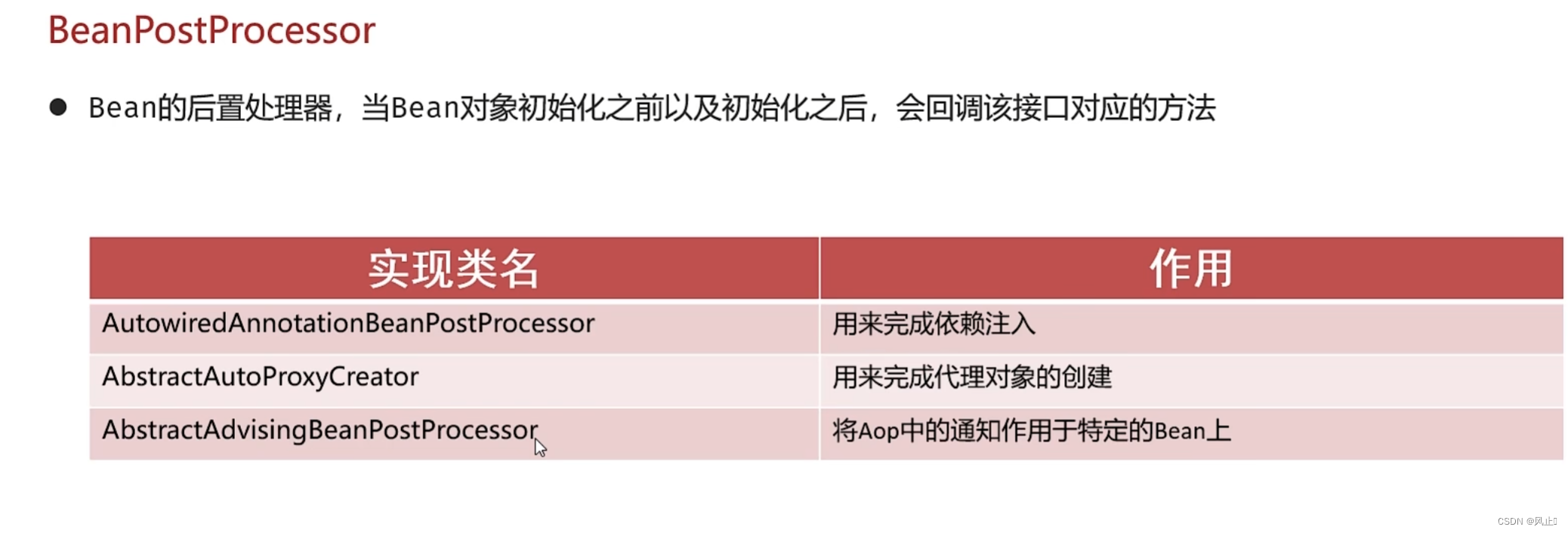
Spring源码：核心类的介绍

1. 前言 核心类代表了Spring框架中最基本的组件和功能&#xff0c;通过介绍这些类&#xff0c;学习者可以更好地理解Spring框架的核心工作原理和关键组件之间的关系。同时&#xff0c;了解这些核心类有助于学习者深入掌握Spring框架的使用和扩展方法。 2. ApplicationContextI…...

编程日记 2024/6/12 13:05:43

未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？

编辑&#xff1a;陈萍萍的公主一点人工一点智能 未来机器人的大脑&#xff1a;如何用神经网络模拟器实现更智能的决策&#xff1f;RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战&#xff0c;在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

编程新知 2026/2/7 23:18:28

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2026/1/22 15:14:25

现代密码学 | 椭圆曲线密码学—附py代码

Elliptic Curve Cryptography 椭圆曲线密码学&#xff08;ECC&#xff09;是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础&#xff0c;例如椭圆曲线数字签…...

编程新知 2026/2/6 7:30:33

12.找到字符串中所有字母异位词

&#x1f9e0; 题目解析 题目描述&#xff1a; 给定两个字符串 s 和 p&#xff0c;找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义&#xff1a; 若两个字符串包含的字符种类和出现次数完全相同&#xff0c;顺序无所谓&#xff0c;则互为…...

编程新知 2026/1/31 12:52:29

使用LangGraph和LangSmith构建多智能体人工智能系统

现在&#xff0c;通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战&#xff0c;比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

编程新知 2026/1/26 13:48:59

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表

设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程，两张表是相同的结构，都有整型主键id字段，需要每次从数据库分批取得2000条数据，用于比较，比较操作的同时可以再取2000条数据，等上一次比较完成之后，开始比较，直到比较完所有的数据。比较操作需要比较…...

编程新知 2025/9/14 5:35:46

VisualXML全新升级 | 新增数据库编辑功能

VisualXML是一个功能强大的网络总线设计工具&#xff0c;专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑&#xff08;如DBC、LDF、ARXML、HEX等&#xff09;&#xff0c;并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

编程新知 2026/2/6 5:51:15

阿里云Ubuntu 22.04 64位搭建Flask流程（亲测）

cd /home 进入home盘 安装虚拟环境&#xff1a; 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境&#xff1a; virtualenv myenv 3、激活虚拟环境&#xff08;激活环境可以在当前环境下安装包&#xff09; source myenv/bin/activate 此时&#xff0c;终端…...

编程新知 2026/1/29 20:04:46

如何在Windows本机安装Python并确保与Python.NET兼容

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…...

编程新知 2026/2/8 0:47:08

数据结构：泰勒展开式：霍纳法则（Horner‘s Rule）

目录 &#x1f50d; 若用递归计算每一项&#xff0c;会发生什么&#xff1f; Horners Rule&#xff08;霍纳法则&#xff09; 第一步&#xff1a;我们从最原始的泰勒公式出发 第二步&#xff1a;从形式上重新观察展开式 &#x1f31f; 第三步&#xff1a;引出霍纳法则&…...

编程新知 2026/2/4 23:58:11