当前位置： 首页 > news >正文

音视频开发26 FFmpeg 时间问题整理

news 2026/3/28 8:44:22

time_base 、pts、dts、duration

  • time_base：时间基，所谓时间基表示的就是每个刻度是多少秒 ，例如
    • 如果把1秒分为25等份，你可以理解就是一把尺，那么每一格表示的就是1/25秒。此时的time_base={1，25} ，
    • 如果你是把1秒分成90000份，每一个刻度就是1/90000秒，此时的time_base={1，90000}。
    • 在ffmpeg中。av_q2d(time_base)=每个刻度是多少秒
  • PTS：Presentation Time Stamp。PTS主要用于度量解码后的视频帧什么时候被显示出来，即显示时间戳，某一帧视频什么时候开始显示
    • pts的值就是占多少个时间刻度（占多少个格子）。它的单位不是秒，而是时间刻度。
  • DTS：Decode Time Stamp。DTS主要是标识读入内存中的帧数据流在什么时候开始送入解码器中进行解码，即解码时间戳
  • duration：某一帧视频显示持续时间，duration和pts单位一样，duration表示当前帧的持续时间占多少格。

不同结构体的 time_base

1、AVStream的time_base的单位是秒。每种格式的time_base的值不一样，根据采样来计算，比如mpeg的pts、dts都是以90kHz来采样的，所以采样间隔就是1/900000秒。

2、AVCodecContext的time_base单位同样为秒，不过精度没有AVStream->time_base高，大小为1/framerate。

3、AVPacket下的pts和dts以AVStream->time_base为单位(数值比较大)，时间间隔就是AVStream->time_base。

4、AVFrame里面的pkt_pts和pkt_dts是拷贝自AVPacket，同样以AVStream->time_base为单位；而pts是为输出(显示)准备的，以AVCodecContex->time_base为单位。

5、输入流InputStream下的pts和dts以AV_TIME_BASE为单位(微秒)，至于为什么要转化为微秒，可能是为了避免使用浮点数。

6、输出流OutputStream涉及音视频同步，结构和InputStream不同，暂时只作记录，不分析

相关文章：

音视频开发26 FFmpeg 时间问题整理

time_base 、pts、dts、duration time_base：时间基，所谓时间基表示的就是每个刻度是多少秒 ，例如 如果把1秒分为25等份，你可以理解就是一把尺，那么每一格表示的就是1/25秒。此时的time_base{1，25} &#xf…...

编程日记 2024/6/12 15:58:49

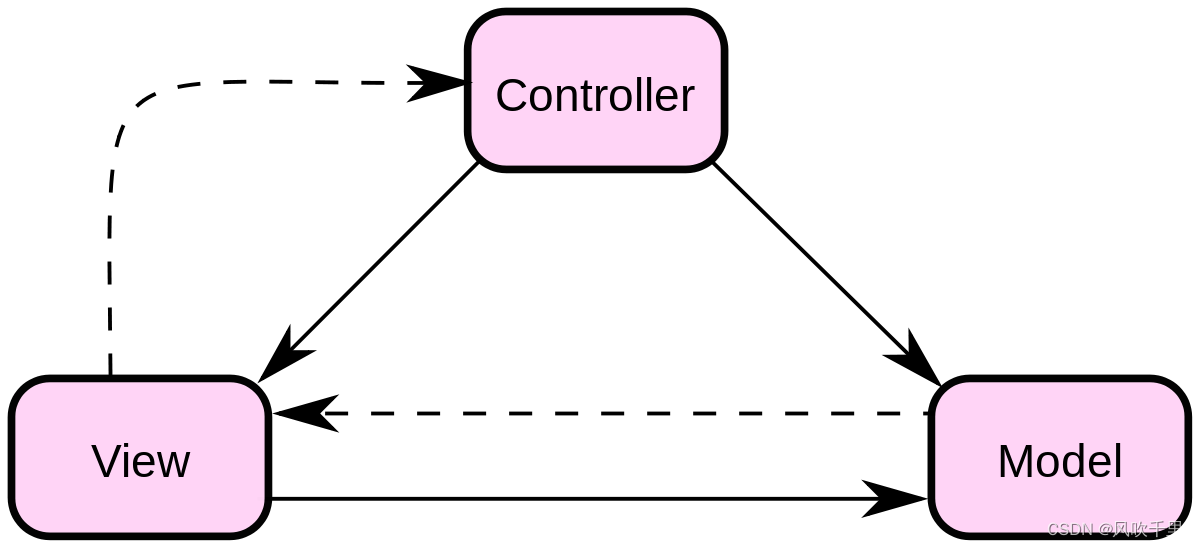
设计模式之MVC模式

文章目录 MVC模式概要意图主要解决的问题使用场景实现方式关键代码应用实例特点优点缺点 使用建议注意事项 代码实现 MVC模式 MVC 模式代表 Model-View-Controller（模型-视图-控制器） 模式。这种模式用于应用程序的分层开发。 Model（模型&a…...

编程日记 2024/6/12 15:57:48

u盘数据要在哪台电脑上恢复？u盘数据恢复后保存在哪里

在数字化时代，U盘已成为我们日常生活中不可或缺的数据存储设备。然而，由于各种原因，U盘中的数据可能会意外丢失，这时数据恢复就显得尤为重要。但是，很多人对于在哪台电脑上进行U盘数据恢复以及恢复后的数据应保存在哪里…...

编程日记 2024/6/12 15:56:47

Selenium 定位编辑框有span

当使用Selenium进行网页自动化测试时，定位一个包含span元素的编辑框可能会有些棘手，因为span通常用于对其他HTML元素进行分组或应用样式，而不一定是真正的可输入字段。不过，一旦我们确定了正确的策略，定位编辑框还是相…...

编程日记 2024/6/12 15:54:44

mac 安装HomeBrew

目录 一、HomeBrew是什么？二、HomeBrew命令1、检查是否安装HomeBrew2、更新brew版本 三、安装HomeBrew1、官网安装2、100%成功安装 一、HomeBrew是什么？ homebrew是一款Mac OS平台下的软件包管理工具，拥有安装、卸载、更新、查看、搜索等功能…...

编程日记 2024/6/12 15:53:43

Windows C++: 剪切板内容获取

获取Windows用户的剪切操作是部分程序的需求，我们同样可以利用这个功能做一个小工具来记忆曾经的复制内容。 代码示例 if (OpenClipboard(nullptr)) {// 打开剪贴板HANDLE hClipboardData GetClipboardData(CF_UNICODETEXT);// 获取剪贴板中的Unicode文本数据if …...

编程日记 2024/6/12 15:52:42

1panel运维面板

文章目录 引言I 安装防火墙II 借助运维面板1panel运维面板安装nacos 引言 在 SSH 终端输入以下命令来查看面板入口: 1pctl user-info 提示：修改密码可执行命令：1pctl update password I 安装防火墙 https://1panel.cn/docs/user_manual/hosts/firewall…...

编程日记 2024/6/12 15:51:40

人工智能GPT-4o？

对比分析 在讨论GPT-4o时，我们首先需要了解其前身，即GPT-4，以及其之前的版本。GPT系列从GPT-1到GPT-4经历了多次迭代，每一次都带来了显著的进步。 GPT-4 vs GPT-4o： 1. **参数规模：** GPT-4o在参数规模上…...

编程日记 2024/6/12 15:48:37

python之语法糖

一.语法糖 语法糖不是糖,而是编程语言中的某些特殊写法,这些写法让书写起来更加简洁,容易理解,因此被叫做语法糖 二.语法糖分类 数字分隔符 a 10_0000_0000交换变量值 a 1;b 2 a,b b,a连续比较式 a 90 if 80<a<100: print(‘优秀’)字符串乘法 a ‘_’*10列表拼…...

编程日记 2024/6/12 15:46:34

纷享销客海外合规观点与方案：个人隐私数据保护与数据出入境

出海&#xff0c;已不再是企业的“备胎”&#xff0c;而是必须面对的“大考”&#xff01;在这个全球化的大潮中&#xff0c;有的企业乘风破浪&#xff0c;勇攀高峰&#xff0c;也有的企业在异国他乡遭遇了“水土不服”。 面对“要么出海&#xff0c;要么出局”的抉择&#xf…...

编程日记 2024/6/12 15:45:32

公司面试题总结（四）

19.请解释什么是事件代理&#xff0c;应用场景 ⚫ 事件流的都会经过三个阶段&#xff1a; 捕获阶段 -> 目标阶段 -> 冒泡阶段&#xff0c;而事件委托就是 在冒泡阶段完成 ⚫ 事件委托&#xff0c;会把一个或者一组元素的事件委托到它的父层或者更外层元素上&#xf…...

编程日记 2024/6/12 15:44:31

守护山川，联通希望 —— 北斗户外应急呼叫柱：野外安全的守护神

在大自然的怀抱中&#xff0c;每一次探险和巡检都是对未知的挑战&#xff0c;也是对安全的考验。北斗户外应急呼叫柱&#xff0c;以科技创新为基石&#xff0c;致力于在最偏远、最危险的环境中搭建起生命的桥梁&#xff0c;确保每一次求救都能被听见&#xff0c;每一处危机都能…...

编程日记 2024/6/12 15:43:29

使用canvas制作一个无人机旋转特效

​ 使用HTML5的Canvas API来制作一个无人机旋转特效。这个特效将包括一个无人机图标&#xff08;你可以使用任何你喜欢的图标&#xff09;&#xff0c;它会在一个固定的位置旋转。 首先&#xff0c;我们需要创建一个HTML文件&#xff0c;然后在其中添加一个canvas元素。canvas…...

编程日记 2024/6/12 15:42:28

感受风的速度~2024COSP上海国际户外展为您的骑行之旅锦上添花

夏天已经到来 你是在家里宅着 还是出去晒太阳呢 若是还没抉择好 不如来一场畅快淋漓的追风之旅 抬头可见蓝天白云 低头便是美丽风景 无论是在凉亭闲聊的人们 还是竞相绽放的花朵 每一个场景都令人难忘 骑累了 就到附近的座椅上小憩一番 不用刻意追求速度 尽享“慢…...

编程日记 2024/6/12 15:41:27

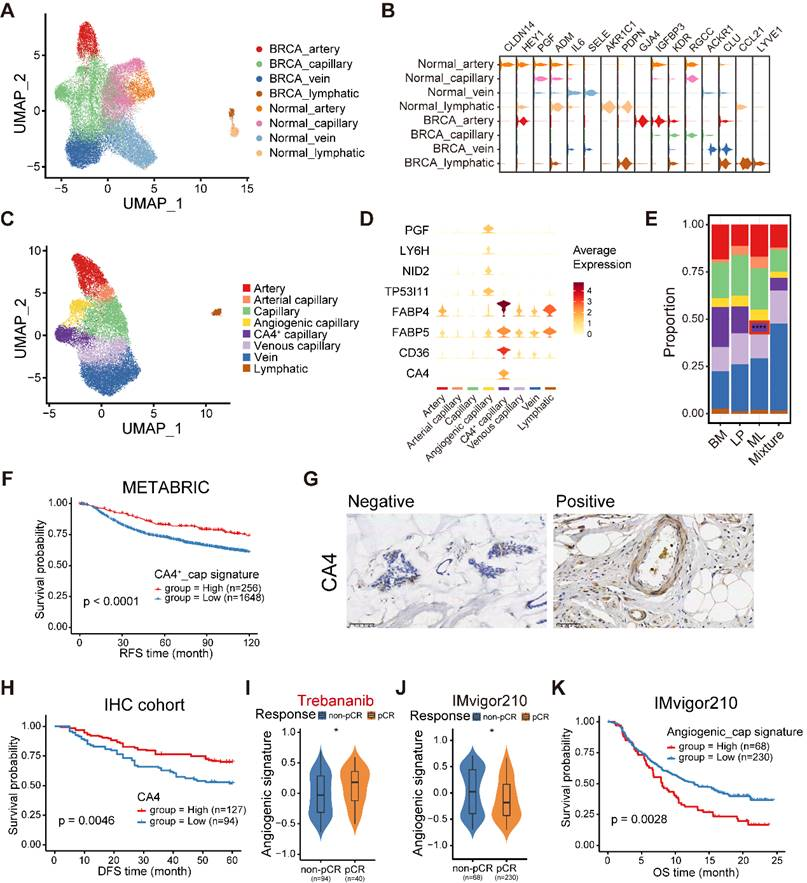
冲12分top刊｜乳腺癌单细胞细分亚型的正确打开方式

说在前面 学习一下一篇自测数据工作量叠满的单细胞文章&#xff0c;也算是多组学的了&#xff0c;bulkRNAscRNA&#xff0c;还有个伪RNA。 整体是一个单细胞分小群的研究思路&#xff0c;分出三种上皮细胞亚群&#xff08;BM、LP、ML&#xff09;&#xff0c;在功能、免疫、预…...

编程日记 2024/6/12 15:40:25

1-Maven-settings配置

1-Maven-settings配置 整理下Maven工具的使用。 【本地仓库、私服、镜像仓库、远程仓库、中央仓库】 本文基于阅读其他博客和对公司Maven配置的学习整理出来的。希望通过本此学习能对Maven有个整体性的掌控。 顺序&#xff1a;profile.repository > pom文件中的repository &…...

编程日记 2024/6/12 15:39:24

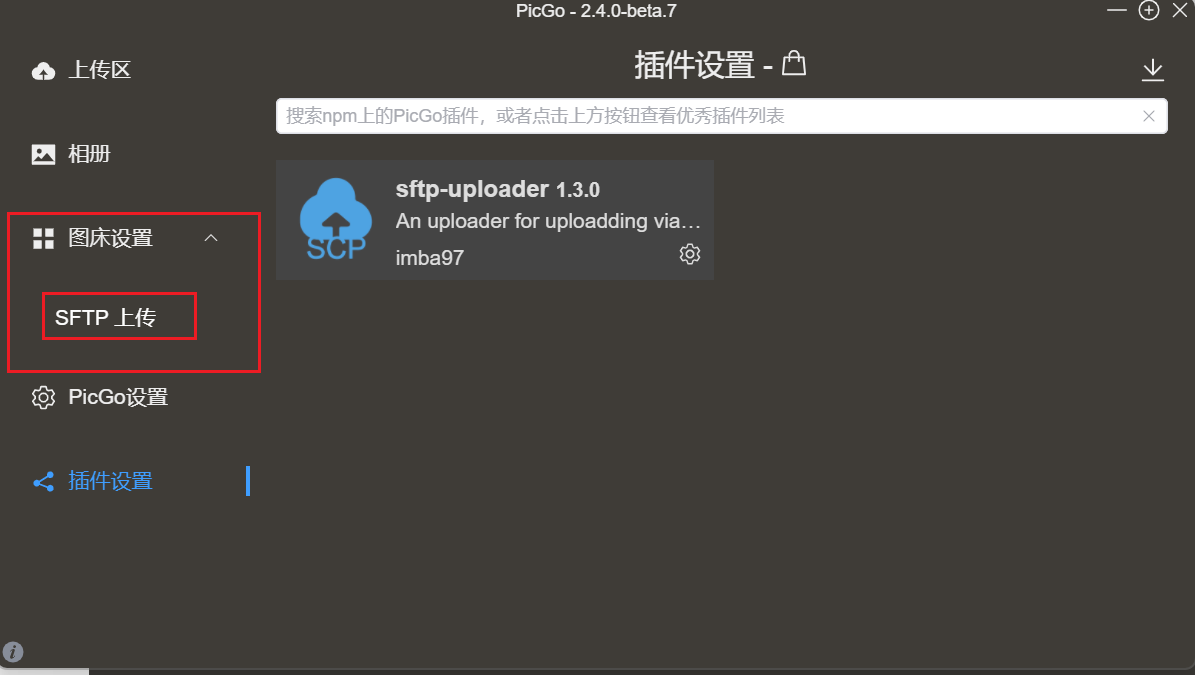
使用服务器搭建个人图床

前置条件 云服务器picGo软件，下载地址开始搭建 发布站点 该步骤不一一说明，主要说明搭建图床的步骤。 可以直接使用nginx或者宝塔面板，发布一个静态资源的文件夹。 假如我发布的文件路径是/www/img，访问地址是http://cc.cc.cc（没有域名ip地址也行） 在img下建立两个文件夹…...

编程日记 2024/6/12 15:34:20

探索 doc 和 docx 文件格式的区别

人不走空 &#x1f308;个人主页&#xff1a;人不走空 &#x1f496;系列专栏&#xff1a;算法专题 ⏰诗词歌赋&#xff1a;斯是陋室&#xff0c;惟吾德馨 目录 &#x1f308;个人主页&#xff1a;人不走空 &#x1f496;系列专栏&#xff1a;算法专题 ⏰诗词歌…...

编程日记 2024/6/12 15:33:18

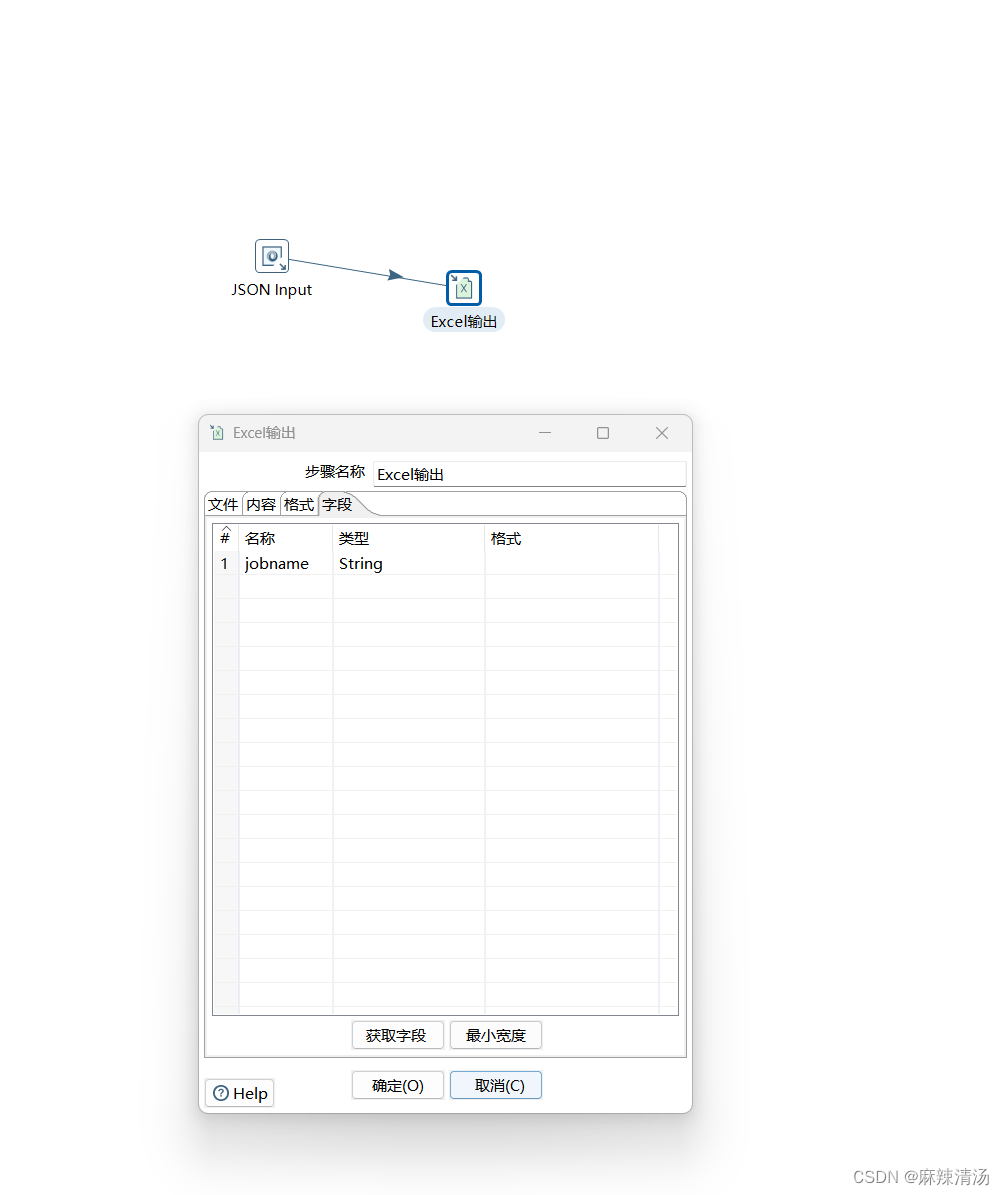
kettle学习（利用jsonPath定位，json文件转换）

kettle学习&#xff08;利用jsonPath定位&#xff0c;json文件转换&#xff09; 于数据处理的广袤天地间&#xff0c;我们时常需应对各类繁杂状况与各式格式。Kettle 作为极具威力的数据集成利器&#xff0c;赋予了我们诸多功能与无限可能此次博客里&#xff0c;我们将重点投向…...

编程日记 2024/6/12 15:32:17

选到哪里看命

srand()、rand() srand(static_cast<unsigned int>(time(nullptr))) 是 C 中用于初始化随机数生成器&#xff08;Random Number Generator, RNG&#xff09;的一个常用语句。srand 函数是 C 标准库 <cstdlib> 中的一部分&#xff0c;用于设置随机数发生器的种子值…...

编程日记 2024/6/12 15:31:16

Steam创意工坊下载终极指南：WorkshopDL让你轻松获取海量模组

Steam创意工坊下载终极指南&#xff1a;WorkshopDL让你轻松获取海量模组 【免费下载链接】WorkshopDL WorkshopDL - The Best Steam Workshop Downloader 项目地址: https://gitcode.com/gh_mirrors/wo/WorkshopDL 还在为无法访问Steam创意工坊而烦恼吗&#xff1f;Work…...

编程新知 2026/3/28 8:05:41

centos7安装MySQL8.4手册

目录前言一、首先更新插件&#xff0c;并查看当前系统版本二、安装步骤--在线安装1、创建mysql目录2、安装rpm包3、安装 mysql-community-server4、启动MySQL服务5、查看MySQL状态6、设置开机自启动三、查看默认密码四、登录mysql五、修改密码六、开启远程访问1. 修改 MySQL 配…...

编程新知 2026/3/28 6:00:26

如何用Penpot构建完整的用户体验地图和用户旅程：7步打造完美设计流程

如何用Penpot构建完整的用户体验地图和用户旅程&#xff1a;7步打造完美设计流程 【免费下载链接】penpot Penpot - The Open-Source design & prototyping platform 项目地址: https://gitcode.com/GitHub_Trending/pe/penpot Penpot作为开源的设计与原型平台&…...

编程新知 2026/3/28 5:52:12

如何为SortableJS实现高效自动化测试：拖拽功能的完整测试指南

如何为SortableJS实现高效自动化测试&#xff1a;拖拽功能的完整测试指南 【免费下载链接】Sortable Reorderable drag-and-drop lists for modern browsers and touch devices. No jQuery or framework required. 项目地址: https://gitcode.com/gh_mirrors/so/Sortable …...

编程新知 2026/3/28 5:20:01

从LLaVA到Stable Diffusion：多模态融合选拼接还是交叉注意力？一张图帮你做技术选型

多模态融合技术选型指南&#xff1a;拼接与交叉注意力的深度对比与实践策略 在构建现代多模态AI系统时&#xff0c;工程师们常常面临一个关键决策点&#xff1a;如何有效地融合来自不同模态的信息&#xff1f;想象一下&#xff0c;你正在开发一个智能医疗影像分析系统&#xff…...

编程新知 2026/3/28 2:22:51

前端拖拽交互实现：别再只会用原生拖拽了

前端拖拽交互实现&#xff1a;别再只会用原生拖拽了 毒舌时刻这代码写得跟网红滤镜似的——仅供参考。各位前端同行&#xff0c;咱们今天聊聊前端拖拽交互。别告诉我你还在用原生的HTML5拖拽API&#xff0c;那感觉就像在用诺基亚手机——能打电话&#xff0c;但体验太差。 为什…...

编程新知 2026/3/28 1:33:46

深度解析Internet Archive下载器：数字图书馆资源获取的完整方案

深度解析Internet Archive下载器&#xff1a;数字图书馆资源获取的完整方案 【免费下载链接】internet_archive_downloader A chrome/firefox extension that download books from Internet Archive(archive.org) and HathiTrust Digital Library (hathitrust.org) 项目地址:…...

编程新知 2026/3/28 1:23:43

力扣原题《有效的数独游戏》，纯手搓，已验证

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 &#xff0c;验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#xff08;请参考示例图&#xff09; 注…...

编程新知 2026/3/27 22:08:04

避坑指南：电商评论情感分析中常见的5大误区与解决方案

避坑指南&#xff1a;电商评论情感分析中常见的5大误区与解决方案 当你在深夜盯着屏幕上一堆杂乱无章的电商评论数据时&#xff0c;是否曾怀疑过自己的情感分析模型在"说谎"&#xff1f;那些看似完美的准确率数字背后&#xff0c;可能隐藏着连老手都会踩中的陷阱。本…...

编程新知 2026/3/27 20:55:42

RK3576/RK3588 Yolo11 目标检测 Demo

前言 以前的大作业&#xff0c;根据rknn_model_zoo和easy eai示例代码修改&#xff08;缝合&#xff09;&#xff0c;仅供参考 后来我试着模块化一些&#xff0c;方便看&#xff0c;但因为核心代码都是直接用的示例代码&#xff0c;所以有些模块还是耦合&#xff08;composit…...

编程新知 2026/3/27 20:11:07