Day 22:2786. 访问数组中的位置使分数最大
Leetcode 2786. 访问数组中的位置使分数最大
给你一个下标从 0 开始的整数数组 nums 和一个正整数 x 。
你 一开始 在数组的位置 0 处,你可以按照下述规则访问数组中的其他位置:
- 如果你当前在位置 i ,那么你可以移动到满足 i < j 的 任意 位置 j 。
- 对于你访问的位置 i ,你可以获得分数 nums[i] 。
- 如果你从位置 i 移动到位置 j 且 nums[i] 和 nums[j] 的 奇偶性 不同,那么你将失去分数 x 。
请你返回你能得到的 最大 得分之和。
注意 ,你一开始的分数为 nums[0] 。

定义一个数组保存到当前位置且包含当前位置的最大分数,每判断一个元素是,遍历之前的元素进行累加得到最大的分数。
完整代码
class Solution {public long maxScore(int[] nums, int x) {int n = nums.length;long res = nums[0];long[] val = new long[n];val[0] = nums[0];for (int i = 1; i < n; i++) {long max = nums[i];for (int j = 0; j < i; j++) {long t = val[j] + (long) nums[i];if ((nums[j] % 2) != (nums[i] % 2)) t -= x;max = Math.max(max, t);}val[i] = max;res = Math.max(res, val[i]);}return res;}
}
但注意,一开始处于 0 处,所以需要从 0 开始,上述代码是可以不从 0 开始,从自己开始,因此值会偏大。
将当前元素的初始值初始化为 Long.MIN_VALUE,那么从前面开始就比从自己开始小,因此就能避免从自己开始。
完整代码
class Solution {public long maxScore(int[] nums, int x) {int n = nums.length;long res = nums[0];long[] val = new long[n];val[0] = nums[0];for (int i = 1; i < n; i++) {long max = Long.MIN_VALUE;for (int j = 0; j < i; j++) {long t = val[j] + (long) nums[i];if ((nums[j] % 2) != (nums[i] % 2)) t -= x;max = Math.max(max, t);}val[i] = max;res = Math.max(res, val[i]);}return res;}
}
以上的时间复杂度为 O ( n 2 ) O(n^2) O(n2),因为每次都要遍历前面的结果。
保存前面的最优结果,它的最优结果就两种情况:
- 最优结果的最后一个元素是奇数
- 最优结果的最后一个元素是偶数
完整代码
class Solution {public long maxScore(int[] nums, int x) {int n = nums.length;long res = nums[0];long[] dp = new long[]{Integer.MIN_VALUE, Integer.MIN_VALUE};dp[nums[0] % 2] = nums[0];for (int i = 1; i < n; i++) {int part = nums[i] % 2;long cur = Math.max(dp[part] + nums[i], dp[1 - part] + nums[i] - x);res = Math.max(res, cur);dp[part] = Math.max(dp[part], cur);}return res;}
}
要注意最小值的设置,因为里面存在 -x,可能会超出最小值的范围,因此可以设置为 -x或 Integer.MIN_VALUE。
相关文章:

Day 22:2786. 访问数组中的位置使分数最大
Leetcode 2786. 访问数组中的位置使分数最大 给你一个下标从 0 开始的整数数组 nums 和一个正整数 x 。 你 一开始 在数组的位置 0 处,你可以按照下述规则访问数组中的其他位置: 如果你当前在位置 i ,那么你可以移动到满足 i < j 的 任意 …...

理解Es的DSL语法(二):聚合
前一篇已经系统介绍过查询语法,详细可直接看上一篇文章(理解DSL语法(一)),本篇主要介绍DSL中的另一部分:聚合 理解Es中的聚合 虽然Elasticsearch 是一个基于 Lucene 的搜索引擎,但…...
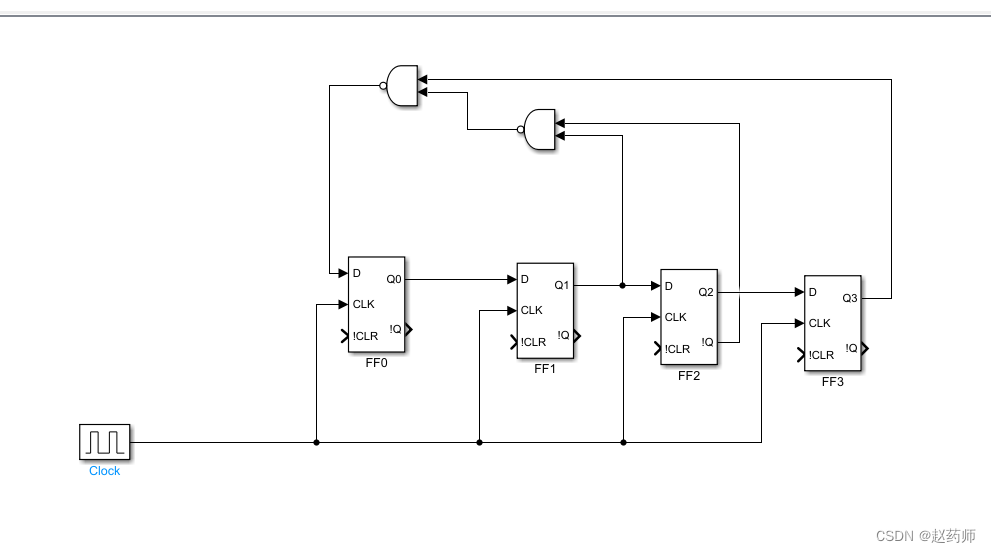
matlab-2-simulink-小白教程-如何绘制电路图进行电路仿真
以上述电路图为例:包含D触发器,时钟CLK,与非门 一、启动simulink的三种方式 方式1 在MATLAB的命令行窗口输入“Simulink”命令。 方式2 在MATLAB主窗口的“主页”选项卡中,单击“SIMULINK”命令组中的Simulink命令按钮。 方式3 从MATLAB…...

CSS从入门到精通——背景样式
目录 背景颜色 任务描述 相关知识 背景色 编程要求 背景图片 任务描述 相关知识 背景图片 设置背景图片 平铺背景图像 任务要求 背景定位与背景关联 任务描述 相关知识 背景定位 背景关联 简写背景 编程要求 背景颜色 任务描述 本关任务:在本关…...
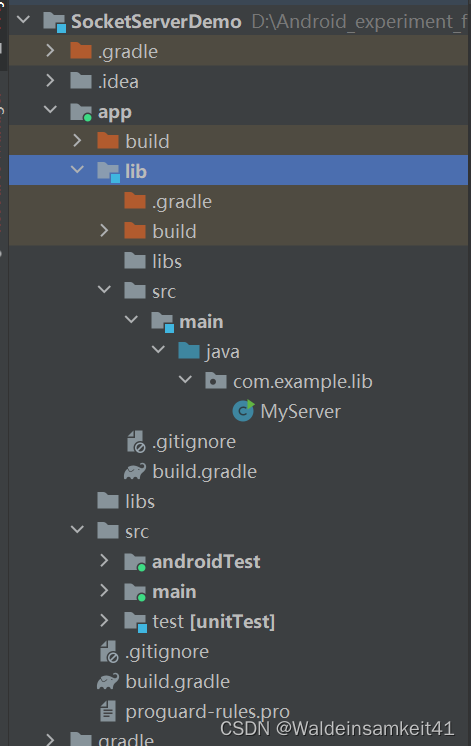
网络编程---Java飞机大战联机
解析服务器端代码 代码是放在app/lib下的src下的main/java,而与之前放在app/src/main下路径不同 Main函数 Main函数里只放着创建MyServer类的一行 public static void main(String args[]){new MyServer();} MyServer构造函数 1.获取本机IP地址 //获取本机IP地…...

一个简单的Oracle函数
CREATE OR REPLACE FUNCTION getyj_zhibiao_value(p_name IN varchar2, p_index IN varchar2) RETURN NUMBER IS -- 定义返回的指标值变量 v_result NUMBER; -- 定义临时变量来存储查询到的指标值 v_index1 VARCHAR2(50); v_index2 VARCHAR2(50); …...
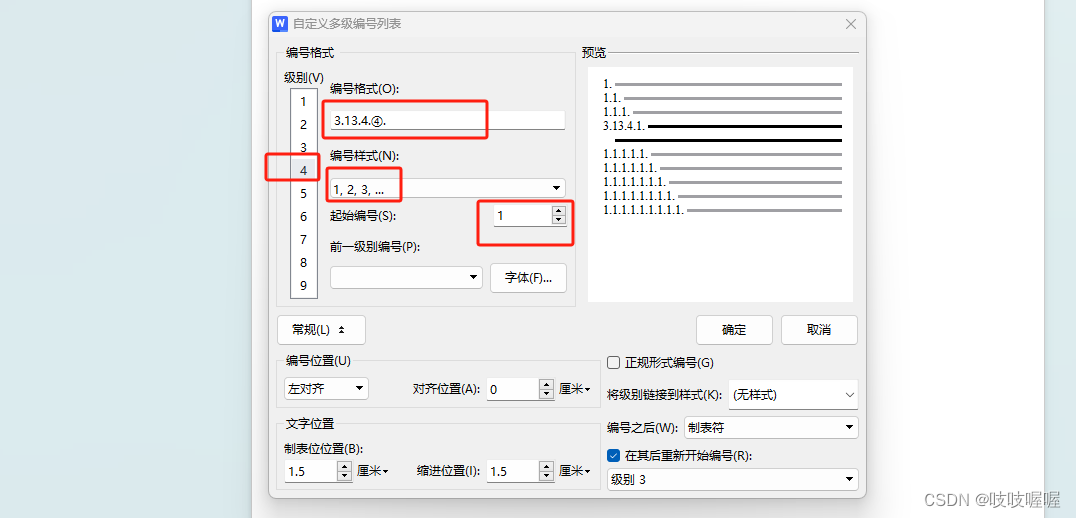
word中根据上级设置下级编号
如上级是3.13.4,如下图 现在想设置下级编码跟随上级逐级显示成3.13.4.1 则在标题功能说明这点击顶部菜单栏的编号按钮,如下图 然后,选择自定义编号-自定义列表-自定义按钮 然后重点是编号格式这一栏,需要手动填写下前三级的编号&…...

【康复学习--LeetCode每日一题】2786. 访问数组中的位置使分数最大
题目描述: 给你一个下标从 0 开始的整数数组 nums 和一个正整数 x 。 你一开始 在数组的位置 0 处,你可以按照下述规则访问数组中的其他位置: 如果你当前在位置 i ,那么你可以移动到满足 i < j 的 任意 位置 j 。 对于你访问的…...

bash和sh区别
bash 和 sh 是两种常用的 Unix Shell,它们有一些区别,特别是在功能和兼容性方面。以下是一些主要的区别: 1. **历史与实现**: - sh(Bourne Shell)是第一个 Unix Shell,最初由 Stephen Bourn…...
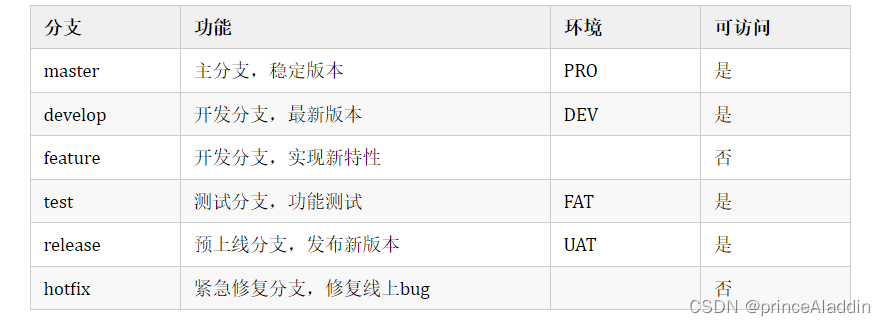
Git 代码管理规范 !
分支命名 master 分支 master 为主分支,也是用于部署生产环境的分支,需要确保master分支稳定性。master 分支一般由 release 以及 hotfix 分支合并,任何时间都不能直接修改代码。 develop 分支 develop 为开发环境分支,始终保持最…...

MGRS坐标
一 概述 MGRS坐标系统,即军事格网参考系统,是北约(NATO)军事组织使用的标准坐标系统。它基于UTM(通用横向墨卡托)系统,并将每个UTM区域进一步划分为100km100km的小方块。这些方块通过两个相连的字母标识,其…...

FreeRTOS简单内核实现4 临界段
文章目录 0、思考与回答0.1、思考一0.2、思考二0.3、思考三 1、关中断1.1、带返回值1.2、不带返回值 2、开中断3、临界段4、应用 0、思考与回答 0.1、思考一 为什么需要临界段? 有时候我们需要部分代码一旦这开始执行,则不允许任何中断打断࿰…...

Scala的字符串插值
Scala的字符串插值 期待您的关注 ☀Scala学习笔记 目录 Scala的字符串插值 1. s插值器: 2. f插值器: 3. raw插值器: 在Scala中,字符串插值是一种方便的方式,可以在字符串中插入变量或表达式的值。Scala支持三种类型…...
EasyGBS服务器和终端配置
服务器配置 修改easygbs.ini sip/host为本机IP,否则终端能登录,无法视频。 [sip] host192.168.3.190 终端用于登录的用户名和密码 default_usertest default_passwordtest1234 default_guest_userguest default_guest_passwordtest1234终端配置 关…...

git配置2-不同的代码托管平台配置不同的ssh key
1. 配置单个ssh key 1.1. 原理1.2. 生成 ssh key1.3. 代码托管平台配置公钥 2. 配置多个ssh key 2.1. 应用场景2.2. 生成两个不同的key2.3. 修改config文件2.4. 配置代码托管平台2.5. 测试是否成功 1. 配置单个ssh key 1.1. 原理 使用ssh命令行工具(git安装成功…...

【CT】LeetCode手撕—102. 二叉树的层序遍历
目录 题目1-思路2- 实现⭐102. 二叉树的层序遍历——题解思路 3- ACM实现3-1 二叉树构造3-2 整体实现 题目 原题连接:102. 二叉树的层序遍历 1-思路 1.借助队列 Queue ,每次利用 ①while 循环遍历当前层结点,②将当前层结点的下层结点放入 …...

Flink 命令行提交、展示和取消作业
Apache Flink 是一个流处理和批处理的开源框架,用于在分布式环境中执行无边界和有边界的数据流。你可以使用 Flink 的命令行界面(CLI)来提交、展示和取消作业。 提交作业 使用 Flink CLI 提交作业的命令格式通常如下: ./bin/fl…...

STM32单片机选型方法
一.STM32单片机选型方法 1.首先要确定需求: 性能需求:根据应用的复杂度和性能要求,选择合适的CPU性能和主频。 内存需求:确定所需的内存大小,包括RAM和Flash存储空间。 外设需求:根据应用所需的功能&…...

gsap动画库的实践
先看效果: gsap动画库 安装插件:npm install gsap <template><div><h1 style"text-align: left">gsap的用法</h1><h1 style"text-align: left">https://gsap.com/resources/get-started</h1>&…...
LeetCode | 387.字符串中的第一个唯一字符
这道题可以用字典解决,只需要2次遍历字符串,第一次遍历字符串,记录每个字符出现的次数,第二次返回第一个出现次数为1的字符的下标,若找不到则返回-1 class Solution(object):def firstUniqChar(self, s):""…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
