代码随想录算法训练营第二十六天
题目:455. 分发饼干
贪心第一题
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。或者小饼干先喂饱小胃口
首先要对 g 和 s进行排序这样才能知道最大的胃口和最大的饼干然后进行遍历即可
两种方法代码如下:
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int index = 0;for(int i = 0; i < s.size(); i++) { // 饼干 先小的满足小的if(index < g.size() && g[index] <= s[i]){ // 胃口index++;}}return index;}
};class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1; // 饼干数组的下标 int result = 0;for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口if (index >= 0 && s[index] >= g[i]) { // 遍历饼干result++;index--;}}return result;}
};题目:376. 摆动序列
这题确实自己想复杂了 自己在想如何删除元素 因为最后只要计数确实最简单的方法就是遇到峰值就++ 单调的就不++
但是这道题目写代码的话细节还是很多的 需要看视频考虑多种情况
这里的局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),这个坡度就可以有两个局部峰值
这是我们思考本题的一个大体思路,但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
完整代码如下:
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff}}return result;}
};题目:53. 最大子数组和
暴力解法的思路,第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for (int i = 0; i < nums.size(); i++) { // 设置起始位置count = 0;for (int j = i; j < nums.size(); j++) { // 每次从起始位置i开始遍历寻找最大值count += nums[j];result = count > result ? count : result;}}return result;}
};使用贪心的话 就是寻找局部极大值
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?
区间的终止位置,其实就是如果 count 取到最大值了,及时记录下来了。
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for (int i = 0; i < nums.size(); i++) {count += nums[i];if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)result = count;}if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和}return result;}
};相关文章:

代码随想录算法训练营第二十六天
题目:455. 分发饼干 贪心第一题 这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。或者小饼干先喂饱小胃口 首先要对 g 和 s进行排序这样才能知道最大的胃口和最大的饼干然后进行遍历即可…...

[面试题]Java【并发】
[面试题]Java【基础】[面试题]Java【虚拟机】[面试题]Java【并发】[面试题]Java【集合】[面试题]MySQL 因为 Java 并发涉及到的内容会非常多,本面试题可能很难覆盖到所有的知识点,所以推荐 《Java并发编程的艺术》 。 Java 线程 线程 通知 等待 线…...

基于VSCode和MinGW-w64搭建LVGL模拟开发环境
目录 概述 1 运行环境 1.1 版本信息 1.2 软件安装 1.2.1 下载安装VS Code 1.2.1.1 下载软件 1.2.1.1 安装软件 1.2.2 下载安装MinGW-w64 1.2.2.1 下载软件 1.2.2.2 安装软件 1.2.3 下载安装SDL 1.2.3.1 下载软件 1.2.3.2 安装软件 1.2.4 下载安装CMake 1.2.4.…...

H5112B 降压恒流芯片12V24V36V48V60V72V100V 1.2ALED 调光无频闪光滑细腻
H5112B多功能LED恒流驱动器是一款具有良好性能与高度集成度的驱动芯片。以下是该产品的主要优点及应用领域的详细分析: 产品优点: 宽电压输入范围:H5112B支持5V至90V的宽电压输入范围,使其能够适应多种不同的电源环境࿰…...

真心建议大家冲一冲新兴领域,工资高前景好【大模型NLP开发篇】
前言 从ChatGPT到新近的GPT-4,GPT模型的发展表明,AI正在向着“类⼈化”⽅向迅速发展。 GPT-4具备深度阅读和识图能⼒,能够出⾊地通过专业考试并完成复杂指令,向⼈类引以为傲的“创造⼒”发起挑战。 现有的就业结构即将发⽣重⼤变…...
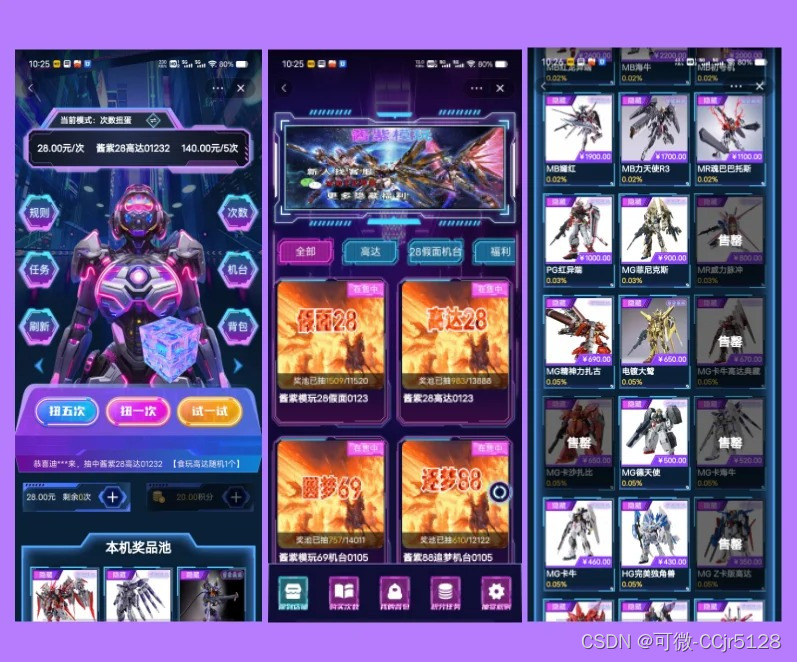
深度剖析淘宝扭蛋机源码:打造趣味性电商活动的秘诀
在当今电商市场中,如何吸引用户的注意力、提升用户的参与度成为了各大电商平台竞相追求的目标。淘宝扭蛋机作为一种新型的电商活动形式,以其趣味性和互动性深受用户喜爱。本文将深度剖析淘宝扭蛋机源码,探讨其如何打造趣味性与互动性并存的电…...

vue3+优化vue-baidu-map中marker点过多导致的页面卡顿问题
场景: 移动端h5中,当我们需要在地图中展示很多marker点坐标的时候,通常会使用 bm-marker ,去循环生成marker点,在数量不多的情况下是没问题的,但是随着数据量的增加,地图就会变得卡顿,以及渲染延…...

PMS助力制造企业高效运营︱PMO大会
全国PMO专业人士年度盛会 北京易贝恩项目管理科技有限公司副总经理朱洪泽女士受邀为PMO评论主办的2024第十三届中国PMO大会演讲嘉宾,演讲议题为“PMS助力制造企业高效运营”。大会将于6月29-30日在北京举办,敬请关注! 议题简要: …...

认识一些分布-关于极值点分布的一些知识
可以参考下面资料: Extreme Value Distribution & the Extreme Value Theory - Statistics How To...

Anaconda环境安装失败的解决方案
链接步骤的补充。 为了运行marlib,需要一个全新的Anaconda环境。但是,不想把文件安装在C盘,会造成空间不足。于是试着在.condarc文件里面改动了路径,具体如图。 上图中,在defaults前面添加了D盘的路径作为安装路径。 …...

mac 本地启动rocketmq
Mac 本地起rocketmq 官网下载:RocketMq官网下载地址 下载后解压 如果电脑配置不高或者不希望rocketmq占用太大内存的,修改配置/bin/runbroker.sh JAVA_OPT"${JAVA_OPT} -server -Xms512m -Xmx512m -Xmn256m"-Xmx4g 初始堆大小 4g -Xms4g 最大…...

数据资产管理的未来趋势:洞察技术前沿,探讨数据资产管理在云计算、大数据、区块链等新技术下的发展趋势
一、引言 随着信息技术的飞速发展,数据已成为企业最重要的资产之一。数据资产管理作为企业核心竞争力的关键组成部分,其发展趋势和技术创新受到了广泛关注。特别是在云计算、大数据、区块链等新技术不断涌现的背景下,数据资产管理面临着前所…...

lwip中server和client的socket、地址和端口号
1、server的socket通过lwip_socket建立: server_sd lwip_socket(AF_INET, SOCK_STREAM, 0);2、client的socket在监听到连接后建立: client_sd lwip_accept(server_sd, (struct sockaddr *)&client_addr_port, (socklen_t *)&size);3、server…...

代码随想录算法训练营Day38|动态规划理论基础、2.斐波那契数、3.爬楼梯、4.使用最小花费爬楼梯
动态规划理论基础 代码随想录 (programmercarl.com) 动态规划(Dynamic Programming,简称DP)是一种算法设计技术,它通过将复杂问题分解为更小的子问题来解决优化问题。动态规划通常用于解决那些具有重叠子问题和最优子结构特性的…...

IIC通信总线
文章目录 1. IIC总线协议1. IIC简介2. IIC时序1. 数据有效性2. 起始信号和终止信号3. 数据格式4. 应答和非应答信号5. 时钟同步6. 写数据和读数据 2. AT24C023. AT24C02读写时序4. AT24C02配置步骤5. 代码部分1. IIC基本信号2. AT24C02驱动代码3. 实验结果分析 1. IIC总线协议 …...
2024 年最新 Python 调用 OpenAi 详细教程实现问答、图像合成、图像理解、语音合成、语音识别(详细教程)
OpenAi 环境安装 首先确保您的计算机上已经安装了 Python。您可以从 Python 官方网站下载并安装最新版本 Python。安装时,请确保勾选 “Add Python to PATH” (添加环境变量)选项,以便在 cmd 命令行中直接使用 Python。 安装 Op…...

git原理解释,windows 10 / ubuntu 24.04 安装使用 github
git的原理 git是赫赫有名的Linux之父Linus Torvalds从2005年起开发的文件版本管理系统,掌控Linux内核这样一个最为重量级的世界产品的Linus为什么要开发这个东西呢?因为Linux系统由全世界的程序员协作维护,对源代码文件的版本控制管理的需求…...
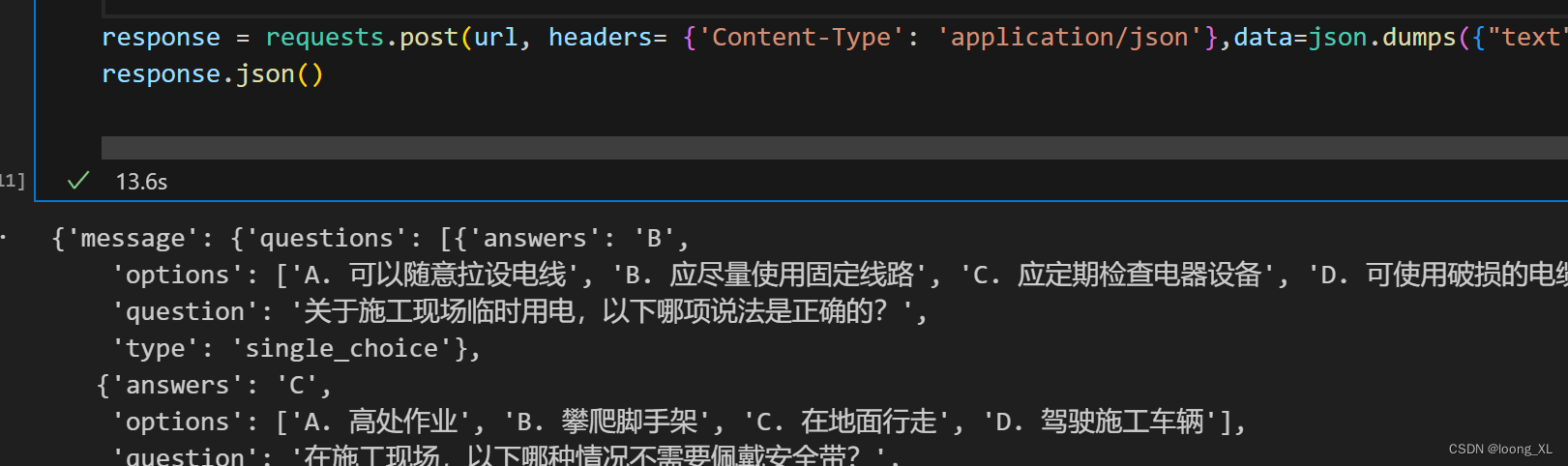
requests post json/data;requests response 接收不同数据
1、requests post json/data 在Python的requests库中,当你发送POST请求时,可以选择使用json参数或data参数来传递数据。这两者之间的主要区别在于它们如何被序列化和发送到服务器。 json参数: 当你使用json参数时,requests库会自…...
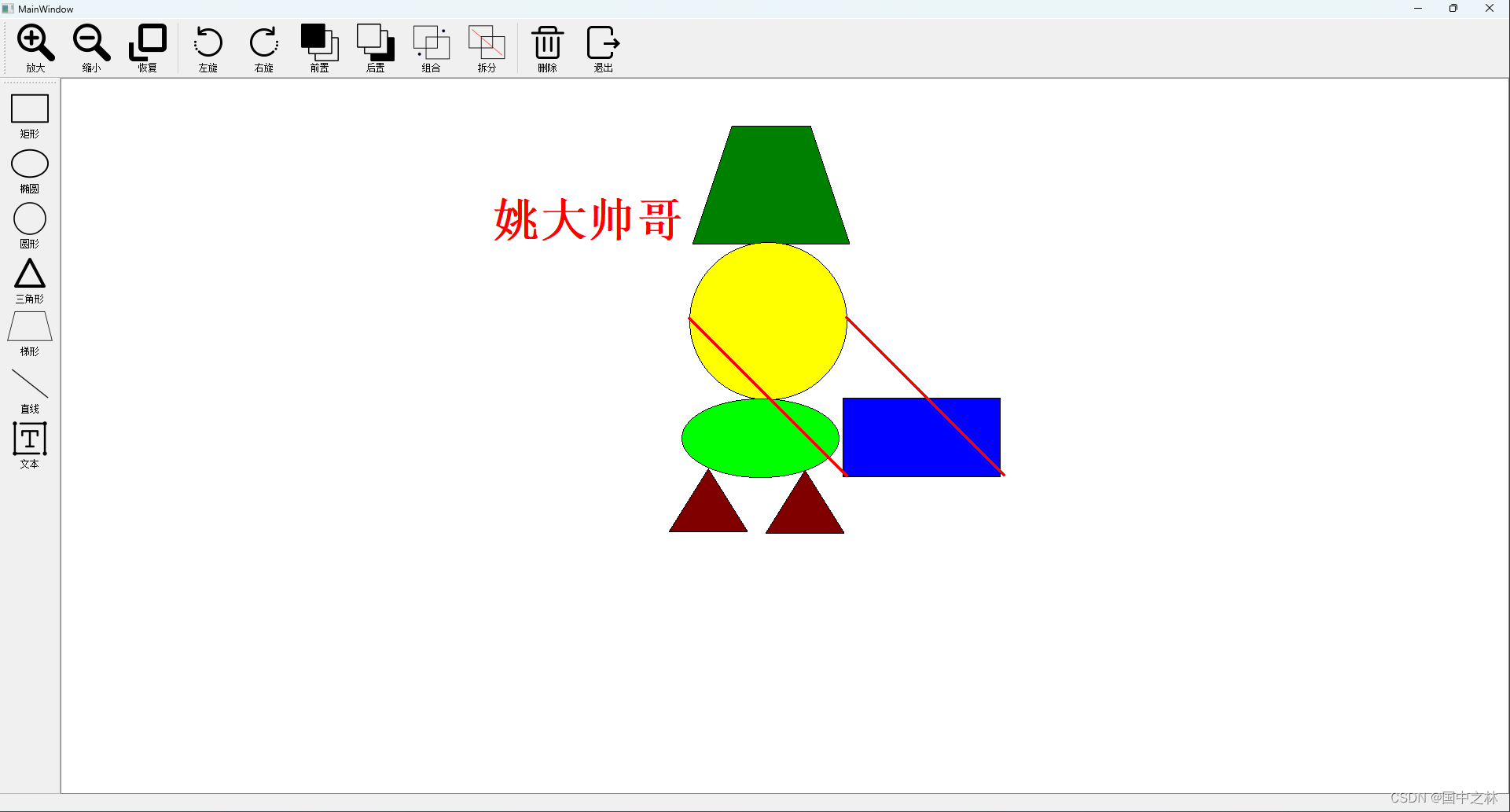
【qt】平面CAD(计算机辅助设计 )项目 上
CAD 一.前言二.界面设计三.提升类四.接受槽函数五.实现图形action1.矩形2.椭圆3.圆形4.三角形5.梯形6.直线7.文本 六.总结 一.前言 用我们上节课刚刚学过的GraphicsView架构来绘制一个可以交互的CAD项目! 效果图: 二.界面设计 添加2个工具栏 需要蔬菜的dd我! 添加action: …...

C++中bool类型的使用细节
C中bool类型的使用细节 ANSIISO C标准添加了一种名叫bool的新类型(对 C来说是新的)。它的名称来源于英国数学家 George Boole,是他开发了逻辑律的数学表示法。在计算中,布尔变量的值可以是true或false。过去,C和C一样,也没有布尔…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
