C/C++函数指针、C#委托是什么?
函数指针
#include<stdio.h>//声明函数指针
typedef int(*Calc)(int a, int b);
int Add(int a, int b)
{return a + b;
}
int Sub(int a, int b) {return a - b;
}int main() {Calc funcPoint1 = &Add;Calc funcPoint2 = ⋐int x = 120;int y = 140;int z = 0;z = Add(x, y);z = funcPoint1(x, y);printf("%d+%d=%d\n", x, y, z);z = Sub(x, y);z = funcPoint2(x, y);printf("%d-%d=%d\n", x, y, z);system("pause");}
一切皆地址
变量(数据):是以某个地址为起点中的一段内存中所存储的值;
函数(算法):是以函数名为地址起点的一段内存中所存储的一组机器语言指令;
C#中委托是什么?
委托(delegate)是函数指针的‘升级版’;
委托的简单使用
- Action委托
- Func委托
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace FunctionPointerExampleCsharp
{class Program{static void Main(string[] args){Calculator ca = new Calculator();Action action = new Action(ca.Report);ca.Report();action.Invoke();action();Func<int, int, int> func = new Func<int, int, int>(ca.Add);Func<int, int, int> func2 = new Func<int, int, int>(ca.Sub);int result=func.Invoke(12, 34);Console.WriteLine(result);result=func2.Invoke(123, 34);Console.WriteLine(result);result =func(12, 34);Console.WriteLine(result);result =func2(123, 34);Console.WriteLine(result);}}class Calculator{public void Report(){Console.WriteLine("Hello,Tom!");}public int Add(int a, int b){return a + b;}public int Sub(int a, int b){return a - b;}}
}相关文章:

C/C++函数指针、C#委托是什么?
函数指针 #include<stdio.h>//声明函数指针 typedef int(*Calc)(int a, int b); int Add(int a, int b) {return a b; } int Sub(int a, int b) {return a - b; }int main() {Calc funcPoint1 &Add;Calc funcPoint2 ⋐int x 120;int y 140;int z 0;z …...

红队攻防渗透技术实战流程:组件安全:JacksonFastJsonXStream
红队攻防渗透实战 1. 组件安全1.1 J2EE-组件Jackson-本地demo&CVE1.1.1 代码执行 (CVE-2020-8840)1.1.2 代码执行(CVE-2020-35728)1.2 J2EE-组件FastJson-本地demo&CVE1.2.1 FastJson <= 1.2.241.2.2 FastJson <= 1.2.471.2.3 FastJson <= 1.2.801.3 J2EE-组…...

Perl 语言学习进阶
一、如何深入 要深入学习Perl语言的库和框架,可以按照以下步骤进行: 了解Perl的核心模块:Perl有许多核心模块,它们提供了许多常用的功能。了解这些模块的功能和用法是深入学习Perl的第一步。一些常用的核心模块包括:S…...

LangGraph实战:从零分阶打造人工智能航空客服助手
❝ 通过本指南,你将学习构建一个专为航空公司设计的客服助手,它将协助用户查询旅行信息并规划行程。在此过程中,你将掌握如何利用LangGraph的中断机制、检查点技术以及更为复杂的状态管理功能,来优化你的助手工具,同时…...

R可视化:R语言基础图形合集
R语言基础图形合集 欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 基础图形可视化 数据分析的图形可视化是了解数据分布、波动和相关性等属性必…...
mysql导入sql文件失败及解决措施
1.报错找不到表 1.1 原因 表格创建失败,编码问题mysql8相较于mysql5出现了新的编码集 1.2解决办法: 使用vscode打开sql文件ctrlh,批量替换,替换到你所安装mysql支持的编码集。 2.timestmp没有设置默认值 Error occured at:20…...

JS:获取鼠标点击位置
一、获取鼠标在目标元素中的点击位置 getClickPos.ts: export const getClickPos (e: MouseEvent) > {return {x: e.offsetX,y: e.offsetY,}; };二、获取鼠标在页面中的点击位置 getClickPos.ts: export const getPageClickPos (e: MouseEvent) > {return {x: e.pa…...
)
使用开源的zip.cpp和unzip.cpp实现压缩包的创建与解压(附源码)
目录 1、使用场景 2、压缩包的创建 3、压缩包的解压 4、CloseZipZ和CloseZipU两接口的区别...

npm 异常:peer eslint@“>=1.6.0 <7.0.0“ from eslint-loader@2.2.1
node 用16版本 npm install npm6.14.15 -g将版本降级到6...
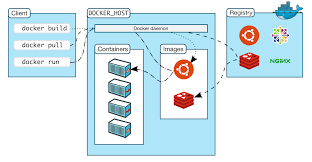
Docker|了解容器镜像层(2)
引言 容器非常神奇。它们允许简单的进程表现得像虚拟机。在这种优雅的底层是一组模式和实践,最终使一切运作起来。在设计的根本是层。层是存储和分发容器化文件系统内容的基本方式。这种设计既出人意料地简单,同时又非常强大。在今天的帖子[1]中…...

使用Python爬取temu商品与评论信息
【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python与爬虫领域研究与开发工作! 【&…...

mybatis学习--自定义映射resultMap
1.1、resultMap处理字段和属性的映射关系 如果字段名和实体类中的属性名不一致的情况下,可以通过resultMap设置自定义映射。 常规写法 /***根据id查询员工信息* param empId* return*/ Emp getEmpByEmpId(Param("empId") Integer empId);<select id…...
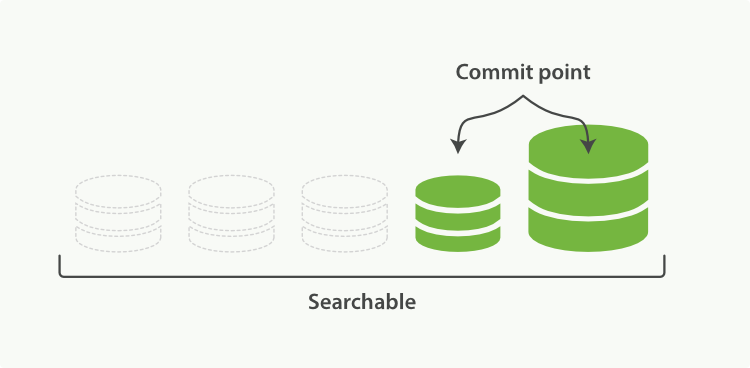
Elasticsearch之写入原理以及调优
1、ES 的写入过程 1.1 ES支持四种对文档的数据写操作 create:如果在PUT数据的时候当前数据已经存在,则数据会被覆盖,如果在PUT的时候加上操作类型create,此时如果数据已存在则会返回失败,因为已经强制指定了操作类型…...

python中装饰器的用法
最近发现装饰器是一个非常有意思的东西,很高级! 允许你在不修改函数或类的源代码的情况下,为它们添加额外的功能或修改它们的行为。装饰器本质上是一个接受函数作为参数的可调用对象(通常是函数或类),并返…...
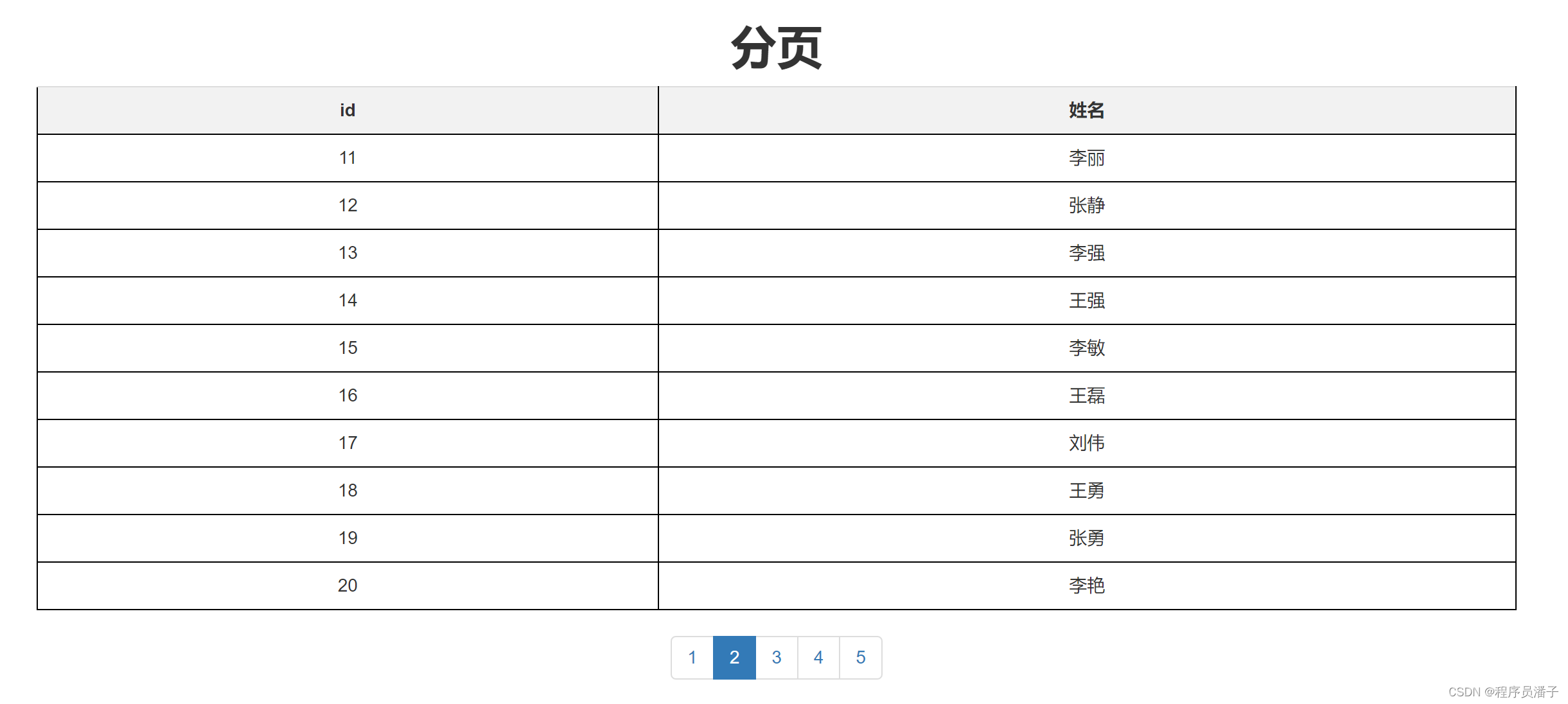
php实现一个简单的MySQL分页
一、案例演示: 二、php 代码 <?php $servername "localhost"; // MySQL服务器名称或IP地址 $username "root"; // MySQL用户名 $password "123456"; // MySQL密码 $dbname "test"; // 要连接…...

算法训练营day23补签
题目1:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode) class Solution { public:int reslut INT_MAX;TreeNode* pre NULL;void trackingback(TreeNode* node) {if(node NULL) return;trackingback(node->left);if(pre ! NULL) {reslut…...

国密SM2JS加密后端解密
1.前端加密 前端加密开源库 sm-crypto 1.1 传统web,下载 sm-crypto 进行打包为 dist/sm2.js 相关打包命令 npm install --save sm-crypto npm install npm run prepublish在web页面引用打包后的文件 <script type"text/javascript" src"<%path %>…...

Cheat Engine.exe修改植物大战僵尸阳光与冷却
Cheat Engine.exe修改植物大战僵尸阳光与冷却 打开Cheat Engine.exe和植物大战僵尸,点CE中文件下面红框位置,选择植物大战僵尸,点击打开 修改冷却: 等冷却完毕,首次扫描0安放植物,再次扫描变动值等冷却完…...
用法)
python内置模块之queue(队列)用法
queue是python3的内置模块,创建堆栈队列,用来处理多线程通信,队列对象构造方法如下: queue.Queue(maxsize0) 是先进先出(First In First Out: FIFO)队列。 入参 maxsize 是一个整数,用于设置…...

Spring Security——结合JWT实现令牌的验证与授权
目录 JWT(JSON Web Token) 项目总结 新建一个SpringBoot项目 pom.xml PayloadDto JwtUtil工具类 MyAuthenticationSuccessHandler(验证成功处理器) JwtAuthenticationFilter(自定义token过滤器) W…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
