力扣hot100: 48. 旋转图像
LeetCode:48. 旋转图像

受到力扣hot100:54. 螺旋矩阵的启发,我们可以对旋转图像按层旋转,我们只需要记录四个顶点,并且本题是一个方阵,四个顶点就能完成图像的旋转操作。
1、逐层旋转
注意到,一层的四个顶点存在一定的位置关系,我们只需要记录四个值:
top_row、bottom_row、left_col、right_col,则上右下左四个顶点分别为:
(top_row,left_col)、(top_row,right_col)、(bottom_row,right_col)、(bottom_row,left_col)
当我们需要更新层时,注意矩阵的下标,只需进行如下操作:
top_row++bottom_row--left_col++right_col--
这样我们就找到了一层的四个顶点,以及更新层的操作。
现在我们只需要逐层更新即可。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int top_row = 0, left_col = 0;int bottom_row = matrix.size() - 1, right_col = matrix.size() - 1;//由于size() > 1,所以可以这样做while(top_row < bottom_row){//方阵,结束条件int step = right_col - left_col;for(int i = 0; i < step; ++ i){int temp;//上换到右temp = matrix[top_row + i][right_col];matrix[top_row + i][right_col] = matrix[top_row][left_col + i];//右换到下int temp2 = temp;temp = matrix[bottom_row][right_col - i];matrix[bottom_row][right_col - i] = temp2;//下换到左temp2 = temp;temp = matrix[bottom_row - i][left_col];matrix[bottom_row - i][left_col] = temp2;//左换到上matrix[top_row][left_col + i] = temp;}//更新层top_row++;bottom_row--;left_col++;right_col--;}return ;}
};
- 我们需要注意一个问题,判断结束条件时,由于方阵行数是
n可以是偶数也可以是奇数,奇数时,上行和下行相等则结束。但如果是偶数时,他俩会交叉,因此是下行大于上行时结束!- 为了在编程时忽略奇偶数的这个问题,我们可以编程时将判断条件更宽泛
- 如果
top_row > bottom_row也不满足条件,那不要写top_row == bottom_row,而是将两者结合起来写,这样可以避免自己的遗漏。
为了节省临时变量,我们也可以按左下转到左上,右下转到左下,右上转到右下,左上转到右上的顺序旋转,这样只需要存储左上的值即可。
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int top_row = 0, left_col = 0;int bottom_row = matrix.size() - 1, right_col = matrix.size() - 1;//由于size() > 1,所以可以这样做while(top_row < bottom_row){//方阵,结束条件int step = right_col - left_col;for(int i = 0; i < step; ++ i){int temp = matrix[top_row][left_col + i];matrix[top_row][left_col + i] = matrix[bottom_row - i][left_col];左换到上matrix[bottom_row - i][left_col] = matrix[bottom_row][right_col - i];//下换到左matrix[bottom_row][right_col - i] = matrix[top_row + i][right_col];//右换到下matrix[top_row + i][right_col] = temp;//上换到右}//更新层top_row++;bottom_row--;left_col++;right_col--;}return ;}
};
和官解的方法二类似。
2、两次翻转等于旋转
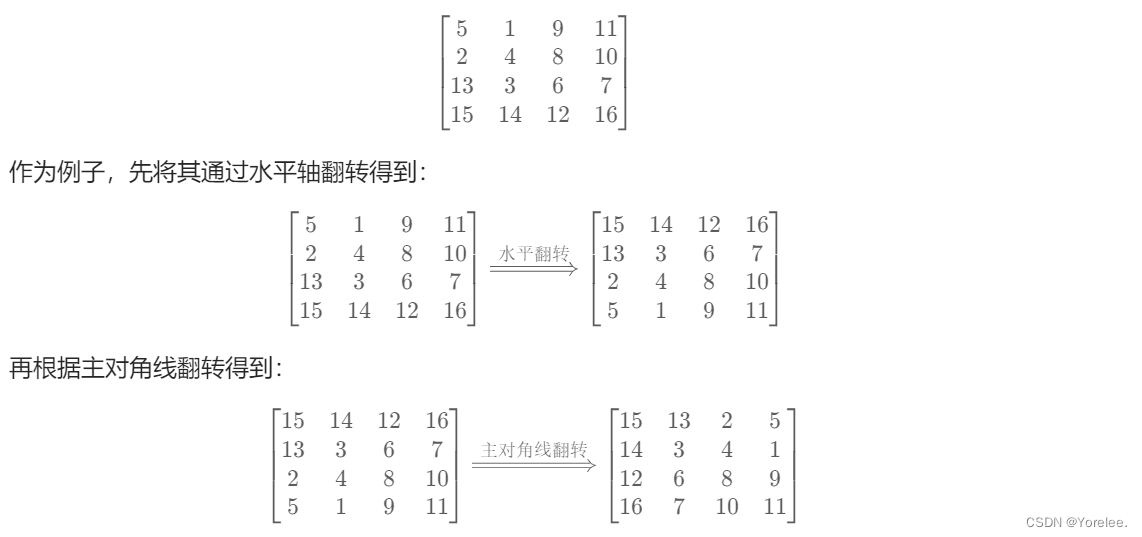
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 水平翻转for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < n; ++j) {swap(matrix[i][j], matrix[n - i - 1][j]);}}// 主对角线翻转for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {swap(matrix[i][j], matrix[j][i]);}}}
};
相关文章:

力扣hot100: 48. 旋转图像
LeetCode:48. 旋转图像 受到力扣hot100:54. 螺旋矩阵的启发,我们可以对旋转图像按层旋转,我们只需要记录四个顶点,并且本题是一个方阵,四个顶点就能完成图像的旋转操作。 1、逐层旋转 注意到࿰…...

基于FPGA的VGA协议实现
目录 一、VGA简介 二、VGA引脚的定义 三、VGA显示原理: 四、VESA标准下的VGA时序: 五、VGA显示模式以及相关参数: 六、数字信号与模拟信号的转换 实战演练一:VGA显示彩条 1、实验目标 2、各模块框图及其波形图 3、模块代…...

Java线程池的抛弃策略
Java线程池的抛弃策略 Java线程池是Java并发编程中非常重要的一个组件。它通过重用已创建的线程来减少线程创建和销毁的开销,从而提高应用程序的性能和响应速度。然而,当线程池中的任务数量超过其处理能力时,就需要一种机制来处理新提交的任…...

【python】Sklearn—Cluster
参考学习来自 10种聚类算法的完整python操作示例 文章目录 聚类数据集亲和力传播——AffinityPropagation聚合聚类——AgglomerationClusteringBIRCH——Birch(✔)DBSCAN——DBSCANK均值——KMeansMini-Batch K-均值——MiniBatchKMeans均值漂移聚类——…...
测试开发面经分享,面试七天速成 DAY 1
1. get、post、put、delete的区别 a. get请求: i. 用于从服务器获取资源。请求参数附加在URL的查询字符串中。 ii. 对服务器的请求是幂等的,即多次相同的GET请求应该返回相同的结果。 iii. 可以被缓存,可以被收藏为书签。 iv. 对于敏感数据不…...

C++ Primer Plus第五版笔记(p201-250)
第六章 函数(下) 在含有return语句的循环后面应该也有一条return语句 不要返回局部对象的引用或指针,当函数结束时临时对象占用的空间也就随之释放掉了,所以两条return语句都指向了不再可用的内存空间。 如果函数返回指针、引用…...
vba学习系列(5)--指定区域指定字符串计数
系列文章目录 文章目录 系列文章目录前言一、需求背景二、vba自定义函数1.引入库 总结 前言 一、需求背景 想知道所有客诉项目里面什么项目最多,出现过多少次。 二、vba自定义函数 1.引入库 引用: CountCharInRange(区域,“字符串”) Function CountCh…...

将Firefox插件导入Edge/Chrome中
目录 将Firefox插件导入Edge/Chrome中前言导出火狐插件.xpi格式插件导入edge/chorme中错误示范1错误示范2修改过程manifest.jsondict文件夹修改backgroundScript.jsinjectedScript.jsdebug过程最终backgroundScript.js和injectedScript.js代码 完工阶段修改后的源码 将Firefox插…...

云计算【第一阶段(14)】Linux的目录和结构
一、Liunx目录结构 1.1、linux目录结构 linux目录结构是树形目录结构 根目录(树根) 所有分区,目录,文件等的位置起点整个树形目录结构中,使用独立的一个"/",表示 1.2、常见的子目录 必须知道 目录路径目…...

Zynq学习笔记--AXI4-Stream到视频输出IP是如何工作的?
目录 1. 简介 2. 原理详解 2.1 示例工程 2.2 AXI4-Stream to Video Out 3. Master/Slave Timing Mode 3.1 Slave Timing Mode 3.2 Master Timing Mode 4. 总结 1. 简介 本文主要介绍了 AXI4-Stream 到视频输出 的内容。其中,示例工程展示了一个具体的设计&…...

2016-2023 年美国农业部作物序列边界
简介 2016-2023 年美国农业部作物序列边界 作物序列边界(CSB)是与美国农业部经济研究局合作开发的,它提供了美国毗连地区的田间边界、作物种植面积和作物轮作的估计数据。该数据集利用卫星图像和其他公共数据,并且是开放源码的,使用户能够对美国种植的商品进行面积和统计…...

数字人源码部署怎么做?如何高效搭建好用的数字人系统?
作为人工智能时代的风口项目,AI数字人自出现之日起便引发了大量的关注。不少创业者都有了搭建数字人系统的想法,但却苦于没有强大的专业背景和雄厚资金支撑,只能在局外徘徊,而这恰恰为数字人源码公司推出的数字人源码部署服务的火…...
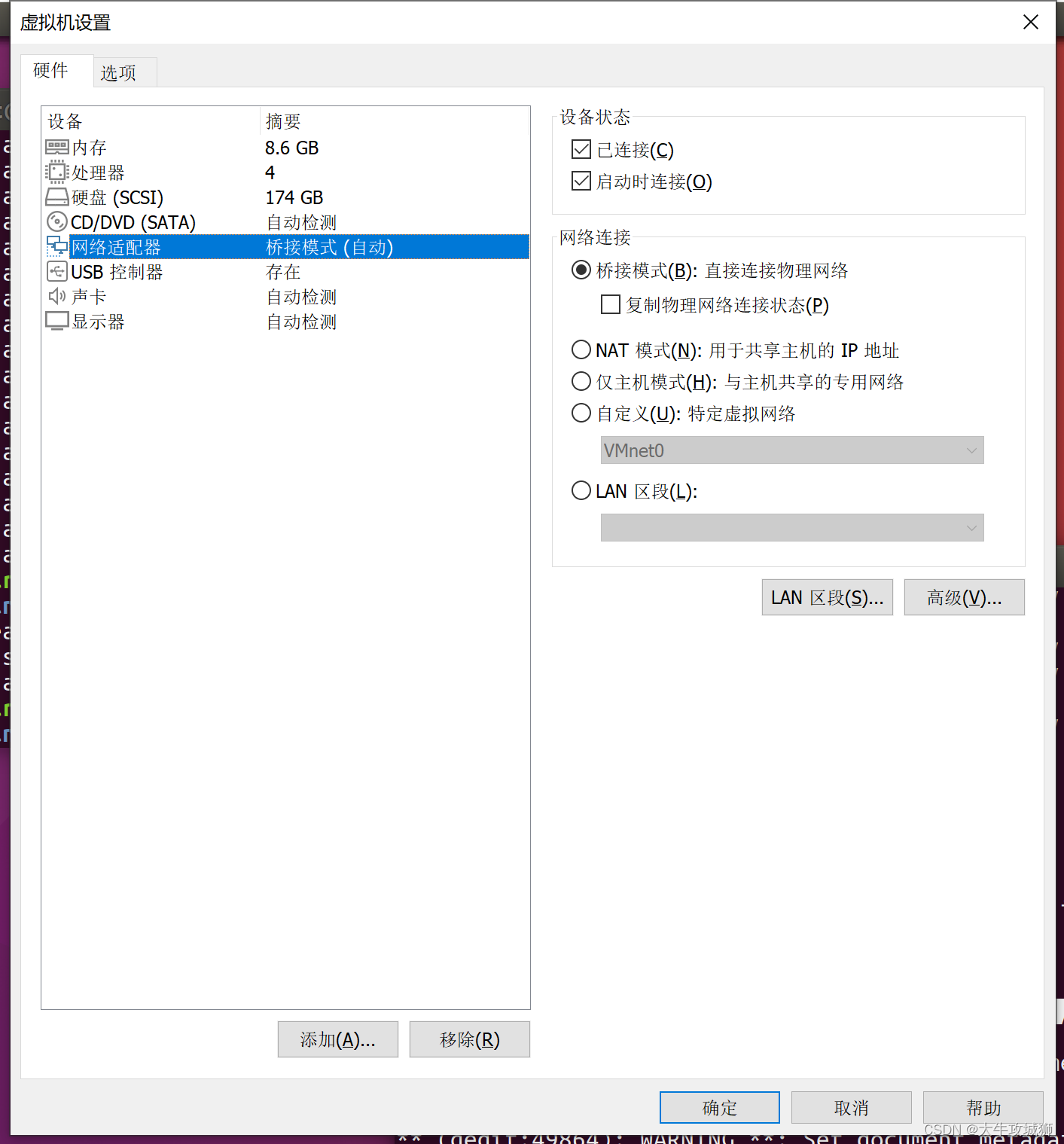
解决虚拟机Ubuntu IP总是掉的问题
问题 嵌入式开发过程中,需要使用NFS/TFTP等等,虚拟机Ubuntu就需要和板卡进行网络连接,但是我发现虚拟机Ubuntu的IP地址经常动不动就掉线,本文记录解决该问题的一些思路。 其实这个问题很简单,我早该想到,…...

[13] CUDA_Opencv联合编译过程
CUDA_Opencv联合编译过程 详细编译过程可见我之前的文章:Win10下OpencvCUDA联合编译详细教程(版本455、460、470,亲测可用!!!)本文给出Windows\linux下的opencvcuda的编译总结,摘自 <基于GP…...

uni-app canvas创建画布
canvasTmp: function(arr2, store_name, successFn, errFun) {let that this;const ctx uni.createCanvasContext(myCanvas);ctx.clearRect(0, 0, 0, 0);/*** 只能获取合法域名下的图片信息,本地调试无法获取* */uni.getImageInfo({ src: arr2[0],success: function(res) {…...
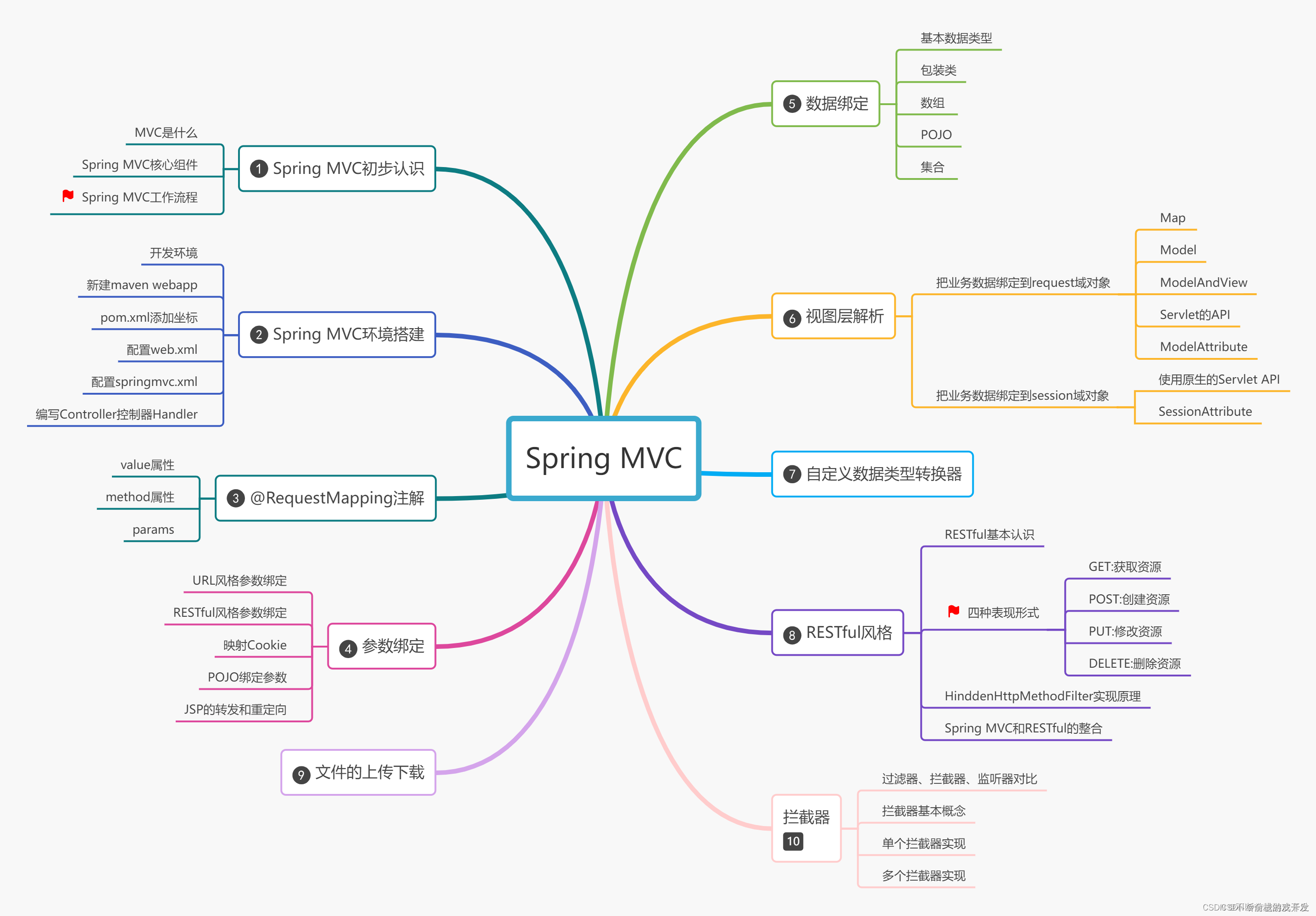
Spring MVC详解(上)
一、Spring MVC初步认识 1.1介绍 Spring MVC是Spring Framework提供的Web组件,全称是Spring Web MVC,是目前主流的实现MVC设计模式的框架,提供前端路由映射、视图解析等功能 Java Web开发者必须要掌握的技术框架 1.2MVC是什么 MVC是一种软件架构思想…...
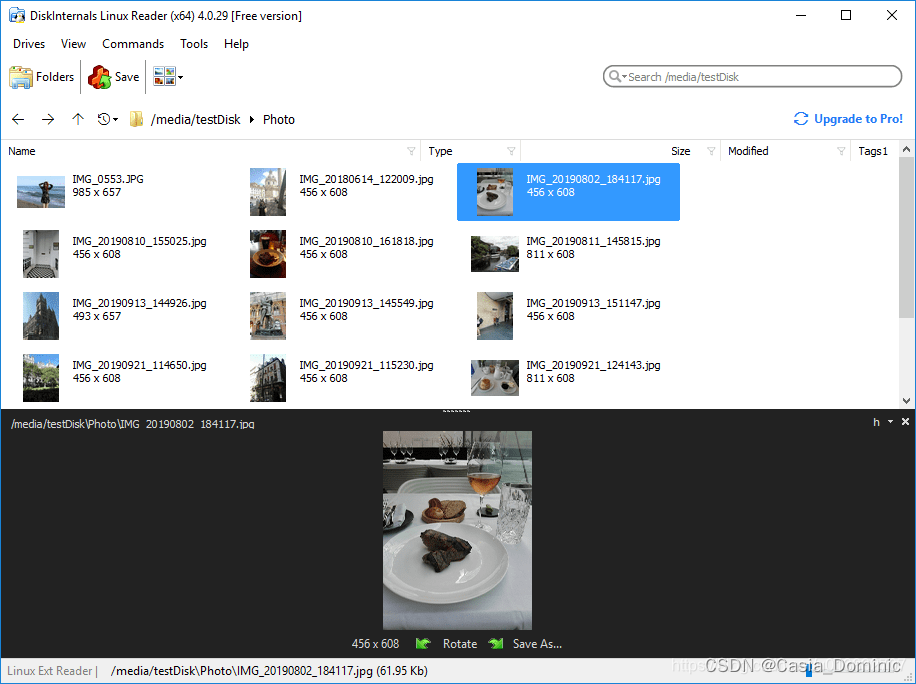
【Linux硬盘读取】Windows下读取Linux系统的文件解决方案:Linux Reader4.5 By DiskInternals
前言 相信做机器视觉相关的很多人都会安装 Windows 和 Linux 双系统。在 Linux 下,我们可以很方便的访问Windows的磁盘,反过来却不行。但是这又是必须的。通过亲身体验,向大家推荐这么一个工具,可以让 Windows 方便的访问 Ext 2/3…...

操作系统—页表(实验)
文章目录 页表1.实验目标2.实验过程记录(1).增加打印页表函数(2).独立内核页表(3).简化软件模拟地址翻译 3.实验问题及相应解答问题1问题2问题3问题4 实验小结 页表 1.实验目标 了解xv6内核当中页表的实现原理,修改页表,使内核更方便地进行用户虚拟地址…...
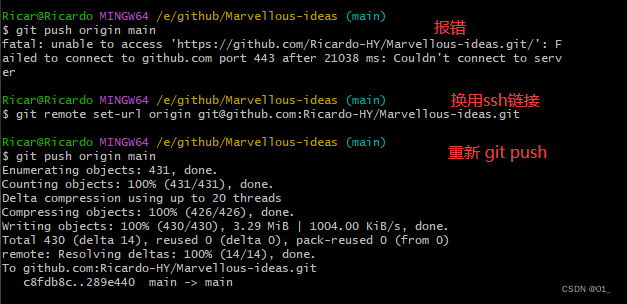
github 本地仓库上传及报错处理
一.本地文件上传 这里为上传部分,关于gitbash安装配置,读者可自行搜索,由于已经安装完成,未进行截图保存,这里便不做赘述。 1.登录git账号并创建一个仓库 点击仓库打开后会看到这个仓库的网址链接(这个链…...
)
【ZZULIOJ】1104: 求因子和(函数专题)
题目描述 输入正整数n(2<n<1000),计算并输出n的所有正因子(包括1,不包括自身)之和。要求程序定义一个FacSum ()函数和一个main()函数,FacSum ()函数计算并返回n的所有正因子之和,其余功能在main()函…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
