求解完全背包问题
题目描述
实现一个算法求解完全背包问题。完全背包问题的介绍如下:
已知一个容量为 totalweight 的背包,有不同重量不同价值的物品,问怎样在背包容量限制下达到利益最大化。
完全背包问题的每个物品可以无限选用
背包问题求解方法的介绍如下:
用符号 Vi 表示第 i 个物品的价值,Wi 表示第 i 个物品的体积,Vi,j 表示当前背包容量为 j 时,前 i 个物品最佳组合对应的价值。
对于当前第 i 个商品,如果包的容量能够装下该物品,即 Wi≤j。此时需要判断装或者不装这个物品的价值对比,选择使价值更大的情况,即 Vi,j=max(Vi+Vi−1,j−Wi,Vi−1,j)
输入描述
第一行为两个数字 otalweight、N,均不超过 1000。totalweight 含义见题干,N 为物品数量。
接下来 N 行,每行两个数字 Wi、Vi,均不超过 1000。含义见题干。
输出描述
输出一行,为在背包容量限制下的最大化利益。
输入输出样例
示例
输入
8 5
3 4
5 5
1 2
2 1
2 3输出
16运行限制
最大运行时间:1s
最大运行内存: 256M
参考答案
T,N = map(int, input().split())
W = []
V = []
for _ in range(N):a,b = map(int, input().split())W.append(a)V.append(b)
dp = [0]*(T+1)
for i in range(N):for j in range(W[i], T+1):dp[j] = max(dp[j], dp[j-W[i]]+V[i])
print(dp[-1])相关文章:

求解完全背包问题
题目描述实现一个算法求解完全背包问题。完全背包问题的介绍如下:已知一个容量为 totalweight 的背包,有不同重量不同价值的物品,问怎样在背包容量限制下达到利益最大化。完全背包问题的每个物品可以无限选用背包问题求解方法的介绍如下&…...

我们为什么使用docker 优点 作用
1. 我们为什么使用Docker? 当我们在工作中,一款产品从开发设计到上线运行,其中需要开发人员和运维工程师,开发人员负责代码编写,开发产品,运维工程师需要测试环境,产品部署。这之间就会有分歧。 就好比我…...

Python每日一练(20230311)
目录 1. 合并两个有序数组 2. 二叉树的右视图 3. 拼接最大数 🌟 每日一练刷题专栏 C/C 每日一练 专栏 Python 每日一练 专栏 1. 合并两个有序数组 给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为…...

202109-3 CCF 脉冲神经网络 66分题解 + 解题思路 + 解题过程
解题思路 根据题意,脉冲源的阈值大于随机数时,会向其所有出点发送脉冲 神经元当v>30时,会向其所有出点发送脉冲,unordered_map <int, vector > ne; //存储神经元/脉冲源的所有出点集合vector 所有脉冲会有一定的延迟&am…...

Aurora简介
Amazon Aurora是一种兼容MySQL和PostgreSQL的商用级别关系数据库,它既有商用数据库的性能和可用性(比如Oracle数据库),又具有开源数据库的成本效益(比如MySQL数据库)。 Aurora的速度可以达到MySQL数据库的…...

【python实操】用python写软件弹窗
文章目录前言组件label 与 多行文本复选框组件Radiobutton单选组件Frame框架组件labelframe标签框架列表框Listboxscrollbar滚动条组件scale刻度条组件spinbox组件Toplevel子窗体组件PanedWindow组件Menu下拉菜单弹出菜单总结针对组件前言 python学习之路任重而道远࿰…...

Ubuntu 常用操作
版本22.04 1、开启 root # 输入新密码 sudo passwd rootUbuntu以root账号登录桌面 默认情况是不允许用root帐号直接登录图形界面的。 Ubuntu 默认使用 GNOME,GNOME 使用 GDM 显示管理器。 为了允许以 root 身份登录到 GNOME,你需要对位于 /etc/…...

井字棋--课后程序(Python程序开发案例教程-黑马程序员编著-第7章-课后作业)
实例2:井字棋 井字棋是一种在3 * 3格子上进行的连珠游戏,又称井字游戏。井字棋的游戏有两名玩家,其中一个玩家画圈,另一个玩家画叉,轮流在3 * 3格子上画上自己的符号,最先在横向、纵向、或斜线方向连成一条…...
谷粒学院开发(三):统一日志、异常及前端准备工作
特定异常处理 ControllerAdvice public class GlobalExceptionHandler {ExceptionHandler(Exception.class) // 指定出现什么异常会被处理ResponseBody // 为了能够返回数据public R error(Exception e) {e.printStackTrace();return R.error().message("执行了全局异常…...
| 机考必刷)
华为OD机试题 - 招聘(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:招聘题目输入输出示例一输入输出说明示例二输入输出说明示例三输…...

关于SQL优化的几点说明
1. ORACLE DBA是如何进行SQL优化的 作为一个Oracle数据库管理员(DBA),SQL优化是他们的日常工作之一,主要目标是优化查询性能,减少查询时间,并提高数据库的整体性能。 以下是Oracle DBA如何进行SQL优化的一般流程: 监控…...
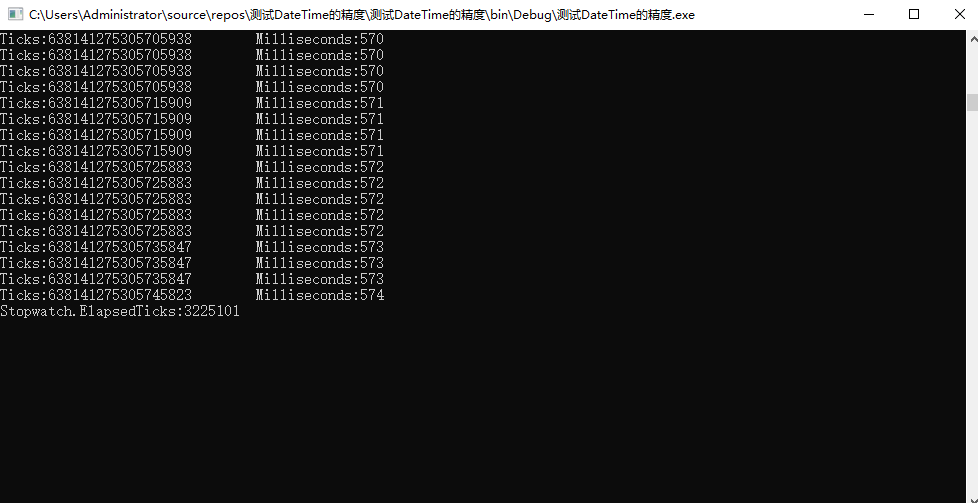
使用高精度秒表StopWatch测试DateTime.Now的精度
StopWatch使用的命名空间:using System.Diagnostics;StopWatch的使用方法:创建Stopwatch对象:stopwatch;stopwatch计时表开启:stopwatch.Start();stopwatch计时表关闭:stopwatch.Stop();计算stopwatch.Stop…...
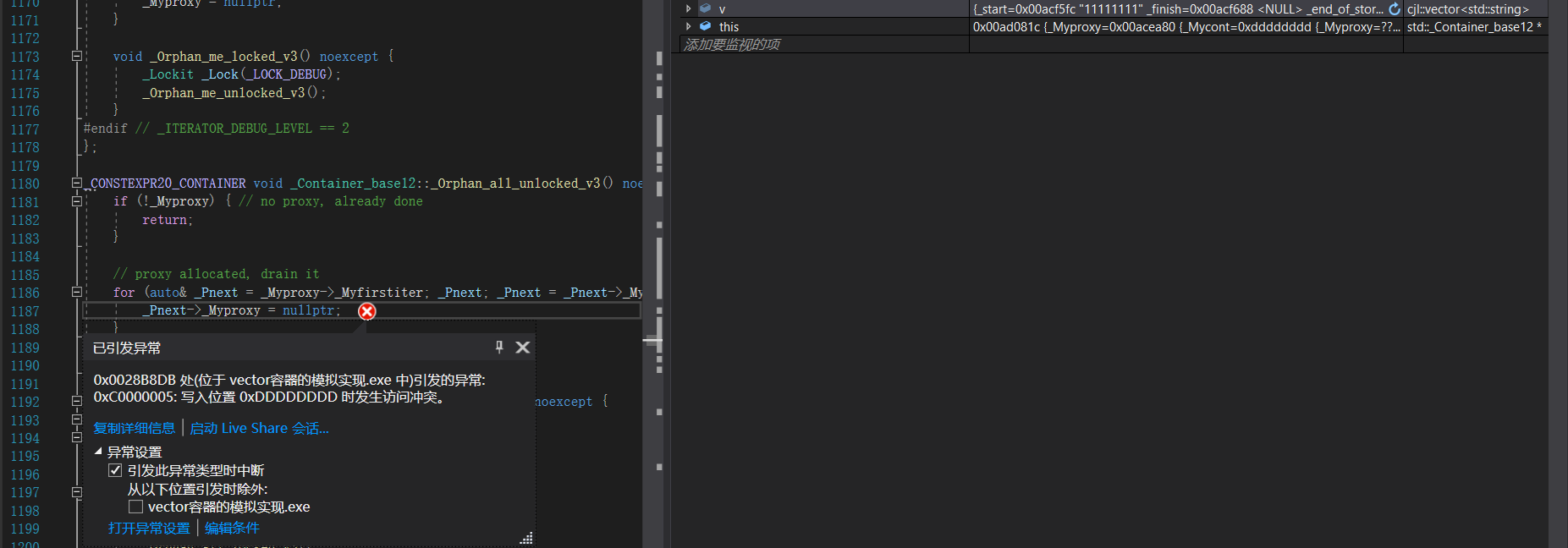
【C++】vector的使用及其模拟实现
这里写目录标题一、vector的介绍及使用1. vector的介绍2. 构造函数3. 遍历方式4. 容量操作及空间增长问题5. 增删查改6. vector二维数组二、vector的模拟实现1. 构造函数2. 迭代器和基本接口3. reserve和resize4. push_back和pop_back5. insert和erase5. 迭代器失效问题5. 浅拷…...
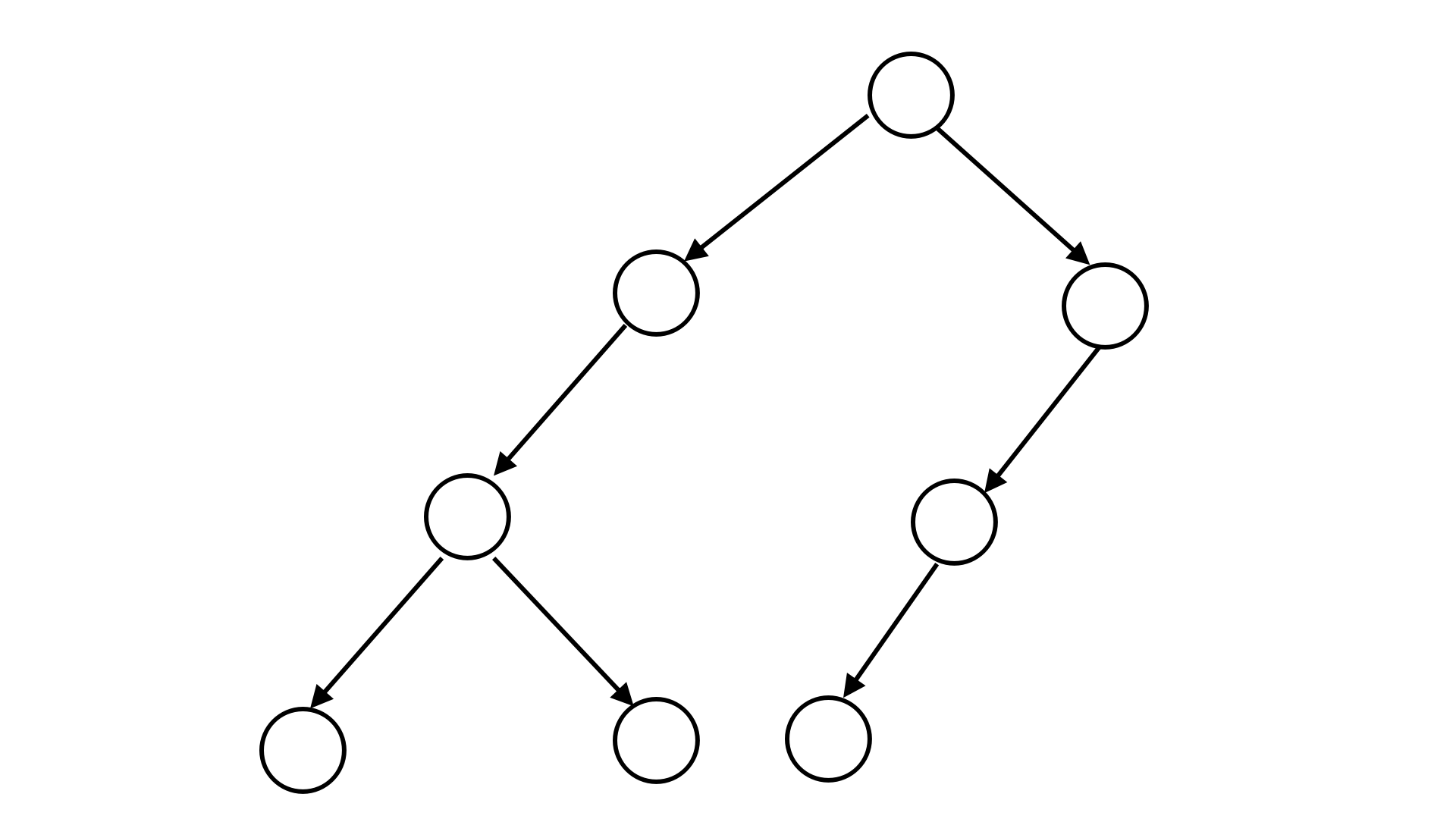
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP状态机DP)一、题目题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定二、分析1、递归建树2、树形DP 状态机DP(1)状态表示(2)状态转移三、…...

BI技巧丨计算组
PowerBI有三大工具,分别是DAX Studio,Tabular Editor和Bravo。 DAX Studio通常我们会用来进行性能分析和DAX调优使用,Bravo一般用来批量格式化DAX,而Tabular Editor主要的功能就是计算组。 计算组这个名词,相信很多小伙…...
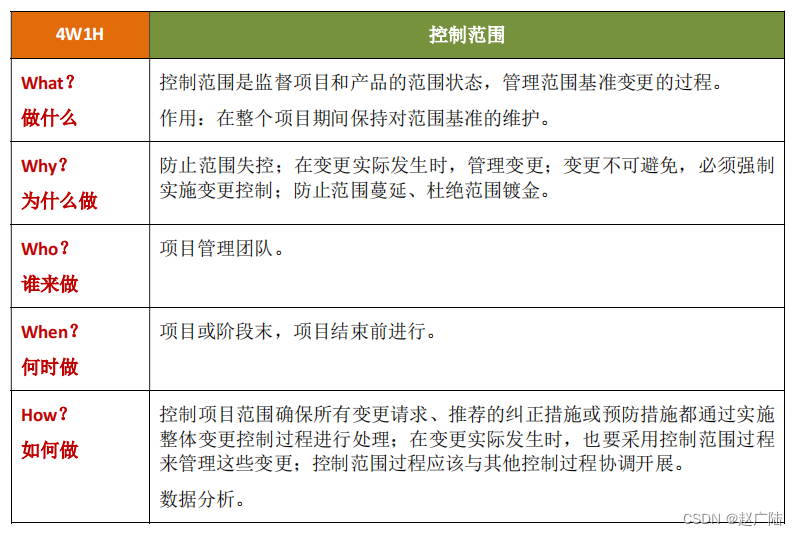
PMP项目管理项目范围管理
目录1 项目范围管理概述2 规划范围管理3 收集需求4 定义范围5 创建 WBS6 确认范围7 控制范围1 项目范围管理概述 项目范围管理包括确保项目做且只做所需的全部工作,以成功完成项目的各 个过程。管理项目范围主要在于定义和控制哪些工作应在项目内,哪些工…...

Flink 定时加载数据源
一、简介 flink 自定义实时数据源使用流处理比较简单,比如 Kafka、MQ 等,如果使用 MySQL、redis 批处理也比较简单 如果需要定时加载数据作为 flink 数据源使用流处理,比如定时从 mysql 或者 redis 获取一批数据,传入 flink 做处…...

ChatGPT、人工智能、人类和一些酒桌闲聊
© 2023 Conmajia Initiated 10th March, 2023 昨天跟某化学家喝酒,期间提到了 ChatGPT。他的评价是:这鬼东西大量输出毫无意义、错漏百出甚至是虚假的信息,“in a confident accent”。例如某次 GPT 针对“描述某某记者”这一问题&#…...

WebRTC开源库内部调用abort函数引发程序发生闪退问题的排查
目录 1、初始问题描述 2、使用Process Explorer工具查看到处理音视频业务的rtcmpdll.dll模块没有加载起来 3、使用Dependency Walker工具查看到rtcmpdll.dll依赖的库有问题 4、更新库之后Debug程序启动时就发生异常,程序闪退 5、VS调试时看不到有效的函数调用堆…...

Golang并发编程
Golang并发编程 文章目录Golang并发编程1. 协程2. channel2.1 channel的创建2.2 使用waitGroup实现同步3. 并发编程3.1 并发编程之runtime包3.2 mutex互斥锁3.3 channel遍历3.3.1 for if遍历3.3.2 for range3.4 select switch3.5 Timer3.5.1 time.NewTimer()3.5.2 Stop、reset…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
