三次插值曲线--插值技术
三次插值曲线
1.1.三次样条曲线
三次样条曲线的基本思想是,在给定的一系列点(称为控制点或数据点)之间,通过一系列三次多项式曲线段来拟合这些点,使得整个曲线既平滑又准确地通过所有控制点。
1.1.1.数学定义
给定一组点 ( P_0, P_1, …, P_n ),其中 ( P_i = (x_i, y_i) ),( x_0 < x_1 < … < x_n )。三次样条曲线由以下性质定义:
1.局部控制:每个曲线段 ( S_i(x) ) 在区间 ( [x_i, x_{i+1}] ) 上是三次多项式。
2.连续性:所有曲线段在连接点处具有相同的一阶导数和二阶导数,即:
( S i ( x i ) = S i + 1 ( x i ) ) ; ( S i ′ ( x i ) = S i + 1 ′ ( x i ) ) ; ( S i ′ ′ ( x i ) = S i + 1 ′ ′ ( x i ) ) ; ( S_i(x_i) = S_{i+1}(x_i) );\\ ( S'_i(x_i) = S'_{i+1}(x_i) );\\ ( S''_i(x_i) = S''_{i+1}(x_i) ); (Si(xi)=Si+1(xi));(Si′(xi)=Si+1′(xi));(Si′′(xi)=Si+1′′(xi));
3.边界条件:通常有两种边界条件,自然边界(Natural)和固定边界(Clamped)。自然边界指在曲线两端,二阶导数为零,即 ( S’‘_0(x_0) = S’'_n(x_n) = 0 )。固定边界则需要指定曲线两端的斜率。
1.1.2.插值公式
对于区间 ( [x_i, x_{i+1}] ) 上的曲线段 ( S_i(x) ),其一般形式为:
y = S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 y=S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3 y=Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3
其中,( a_i, b_i, c_i, d_i ) 是系数,需要通过以下条件确定:
1.对每个S_i(x),其必过型值点P_i, P_{i+1}。
2.对排除首个,末个型值点的每个中间型值点,这些型值点分别位于两个分段函数上。
两个分段函数在此类型值点上一阶导数,二阶导数连续。
3.边界条件。如限定P_0,P_n处二阶导数为0,或指定P__0,P_n处一阶导数。
通过上述三个条件,我们可以唯一确定每一段S_i(x)方程的系数 a_i, b_i, c_i, d_i 。
1.1.3.实例分析
假设现有:
1. P 0 , . . . , P n − 1 共 n 个二维点。对 P i 其坐标为 ( x i , y i ) 。满足 x 0 < . . . < x n − 1 。 2. 给定 P 0 处一阶导数 y 0 ′ ,给定 P n − 1 处一阶导数 y n − 1 ′ 。 1.P_0,...,P_{n-1}共n个二维点。对P_{i}其坐标为(x_{i}, y_{i})。满足x_{0}<...<x_{n-1}。\\ 2.给定P_{0}处一阶导数y'_{0},给定P_{n-1}处一阶导数y'_{n-1}。 1.P0,...,Pn−1共n个二维点。对Pi其坐标为(xi,yi)。满足x0<...<xn−1。2.给定P0处一阶导数y0′,给定Pn−1处一阶导数yn−1′。
要求依据以上信息给出从
P 0 到 P n − 1 的共 n − 1 段三次样条曲线的曲线方程。 P_0到P_{n-1}的共n-1段三次样条曲线的曲线方程。 P0到Pn−1的共n−1段三次样条曲线的曲线方程。
分析:
对第 i 段三次样条函数而言,其形式必然为: y = s i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 x i < = x < x i + 1 ; 我们只需分别求出 a i , b i , c i , d i 即可。 对第i段三次样条函数而言,其形式必然为:\\ y =s_{i}(x)= a_{i}+b_{i}(x-x_{i})+c_{i}(x-x_{i})^2+d_{i}(x-x_{i})^3 x_{i}<=x<x_{i+1};\\ 我们只需分别求出a_{i},b_{i},c_{i},d_{i}即可。 对第i段三次样条函数而言,其形式必然为:y=si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3xi<=x<xi+1;我们只需分别求出ai,bi,ci,di即可。
1.
通过 y = s i ( x i ) = y i ,可得: a i = y i ; 通过y=s_{i}(x_{i})=y_{i},可得: a_{i} = y_{i}; 通过y=si(xi)=yi,可得:ai=yi;
2.
通过 s i ′ ′ ( x i ) = 2 c i 。我们假设每个 P i 处二阶导数为 M i 。则有: c i = M i / 2 ; 通过s''_{i}(x_{i})=2c_{i}。我们假设每个P_{i}处二阶导数为M_{i}。则有:c_{i}=M_{i}/2; 通过si′′(xi)=2ci。我们假设每个Pi处二阶导数为Mi。则有:ci=Mi/2;
3.
通过 S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) 可得: d i = ( M i + 1 − M i ) / [ 6 ( x i + 1 − x i ) ] ; 通过S''_{i}(x_{i+1})=S''_{i+1}(x_{i+1})可得:d_{i}=(M_{i+1}-M_{i})/[6(x_{i+1}-x_{i})]; 通过Si′′(xi+1)=Si+1′′(xi+1)可得:di=(Mi+1−Mi)/[6(xi+1−xi)];
4.
通过 S i ( x i + 1 ) = S i + 1 ( x i + 1 ) 可得: b i = ( y i + 1 − y i ) / ( x i + 1 − x i ) − ( x i + 1 − x i ) [ M i + 1 / 6 + M i / 3 ] 通过S_{i}(x_{i+1})=S_{i+1}(x_{i+1})可得:\\ b_{i}=(y_{i+1}-y_{i})/(x_{i+1}-x_{i})-(x_{i+1}-x_{i})[M_{i+1}/6+M_{i}/3] 通过Si(xi+1)=Si+1(xi+1)可得:bi=(yi+1−yi)/(xi+1−xi)−(xi+1−xi)[Mi+1/6+Mi/3]
通过上述 1 , 2 , 3 , 4 可知,只要知道 M 0 , . . . , M n − 1 便可求出 a i , b i , c i , d i 进而唯一确定每一段的三次样条曲线函数。 下面分析如何求取 M 0 , . . . , M n − 1 。 通过上述1,2,3,4可知,只要知道M_{0},...,M_{n-1}便可求出a_{i},b_{i},c_{i},d_{i}进而唯一确定每一段的三次样条曲线函数。\\ 下面分析如何求取M_{0},...,M_{n-1}。 通过上述1,2,3,4可知,只要知道M0,...,Mn−1便可求出ai,bi,ci,di进而唯一确定每一段的三次样条曲线函数。下面分析如何求取M0,...,Mn−1。
1.
通过 S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) ,可得: M i [ ( x i + 1 − x i ) / 6 ] + M i + 1 [ ( x i + 2 − x i ) / 3 ] + M i + 2 [ ( x i + 2 − x i + 1 ) / 6 ] = ( y i + 2 − y i + 1 ) / ( x i + 2 − x i + 1 ) − ( y i + 1 − y i ) / ( x i + 1 − x i ) ; 上述共有 n − 2 个线性方程。为了依赖线性方程组求解 n 个变量,我们还需要两个。 通过S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1}),可得:\\ M_{i}[(x_{i+1}-x_{i})/6]+M_{i+1}[(x_{i+2}-x_{i})/3]+M_{i+2}[(x_{i+2}-x_{i+1})/6]=\\ (y_{i+2}-y_{i+1})/(x_{i+2}-x_{i+1})-(y_{i+1}-y_{i})/(x_{i+1}-x_{i});\\ 上述共有n-2个线性方程。为了依赖线性方程组求解n个变量,我们还需要两个。 通过Si′(xi+1)=Si+1′(xi+1),可得:Mi[(xi+1−xi)/6]+Mi+1[(xi+2−xi)/3]+Mi+2[(xi+2−xi+1)/6]=(yi+2−yi+1)/(xi+2−xi+1)−(yi+1−yi)/(xi+1−xi);上述共有n−2个线性方程。为了依赖线性方程组求解n个变量,我们还需要两个。
2.
通过 y 0 ′ = S 0 ′ ( x 0 ) ,可得: M 0 [ ( x 1 − x 0 ) / 3 ] + M 1 [ ( x 1 − x 0 ) / 6 ] = ( y 1 − y 0 ) / ( x 1 − x 0 ) ; 通过y'_{0}=S'_{0}(x_{0}),可得:\\ M_{0}[(x_{1}-x_{0})/3]+M_{1}[(x_{1}-x_{0})/6]=(y_{1}-y_{0})/(x_{1}-x_{0}); 通过y0′=S0′(x0),可得:M0[(x1−x0)/3]+M1[(x1−x0)/6]=(y1−y0)/(x1−x0);
3.
通过 y n − 1 ′ = S n − 2 ′ ( x n − 1 ) 可得: M n − 2 [ ( x n − 1 − x n − 2 ) / 6 ] + M n − 1 [ ( x n − 1 − x n − 2 ) / 3 ] = y n − 1 ′ − ( y n − 1 − y n − 2 ) / ( x n − 1 − x n − 2 ) ; 通过y'_{n-1}=S'_{n-2}(x_{n-1})可得:\\ M_{n-2}[(x_{n-1}-x_{n-2})/6]+M_{n-1}[(x_{n-1}-x_{n-2})/3]=\\ y'_{n-1}-(y_{n-1}-y_{n-2})/(x_{n-1}-x_{n-2}); 通过yn−1′=Sn−2′(xn−1)可得:Mn−2[(xn−1−xn−2)/6]+Mn−1[(xn−1−xn−2)/3]=yn−1′−(yn−1−yn−2)/(xn−1−xn−2);
这样,我们构建了n的线性等式。这n个线性等式,可以用矩阵形式表示为:
A n , n M n , 1 = D n , 1 ; M n , 1 = A n , n − 1 D n , 1 ; A_{n,n}M_{n,1}=D_{n,1};\\ M_{n,1}=A^{-1}_{n,n}D_{n,1}; An,nMn,1=Dn,1;Mn,1=An,n−1Dn,1;
这样,我们通过先求取A的逆矩阵,接着便可求出M。然后依据前述求取系数的方法,便可唯一确定每一段的三次样条曲线方程。
1.2.三次参数曲线
这种曲线通过一系列控制点,使用三次多项式来定义曲线上每个点的位置,使得曲线平滑地通过这些控制点。
1.2.1.基本概念
在三次参数样条曲线中,曲线的每个分量(如二维空间中的x和y,或三维空间中的x、y和z)都是参数t的三次多项式。对于给定的一组控制点( P_i(x_i, y_i, z_i) ),曲线的数学表达式可以写作:
P ( t ) = [ x ( t ) , y ( t ) , z ( t ) ] P(t) = [x(t), y(t), z(t)] P(t)=[x(t),y(t),z(t)]
其中,( x(t) ), ( y(t) ), ( z(t) ) 都是参数t的三次多项式:
x ( t ) = a x t 3 + b x t 2 + c x t + d x ; y ( t ) = a y t 3 + b y t 2 + c y t + d y ; z ( t ) = a z t 3 + b z t 2 + c z t + d z ; 其中 t 的含义为当前点距离分段起始点的距离。 x(t) = a_x t^3 + b_x t^2 + c_x t + d_x; \\ y(t) = a_y t^3 + b_y t^2 + c_y t + d_y;\\ z(t) = a_z t^3 + b_z t^2 + c_z t + d_z;\\ 其中t的含义为当前点距离分段起始点的距离。 x(t)=axt3+bxt2+cxt+dx;y(t)=ayt3+byt2+cyt+dy;z(t)=azt3+bzt2+czt+dz;其中t的含义为当前点距离分段起始点的距离。
1.2.2.边界条件
为了确定这些系数( a ), ( b ), ( c ), ( d ),通常需要一些边界条件。常见的边界条件包括:
1.曲线通过控制点:在每个控制点处,t的值设为0或1,确保曲线通过这些点。
2.平滑性:对每个分段函数而言,在区间内二阶连续可导。不同分段函数在邻接点上一阶导数,二阶导数连续。
1.2.3.实际例子
假设现有:
1. P 0 , . . . , P n − 1 共 n 个点。满足相邻的点不重合。 2. P 0 处各个轴关于弧长一阶导数也是已知的,设为 P 0 ′ . x , P 0 ′ . y , P 0 ′ . z 。 3. P n − 1 处各个轴关于弧长一阶导数也是已知的,设为 P n − 1 ′ . x , P n − 1 ′ . y , P n − 1 ′ . z 。 1.P_{0},...,P_{n-1}共n个点。满足相邻的点不重合。\\ 2.P_{0}处各个轴关于弧长一阶导数也是已知的,设为P'_{0}.x,P'_{0}.y,P'_{0}.z。\\ 3.P_{n-1}处各个轴关于弧长一阶导数也是已知的,设为P'_{n-1}.x,P'_{n-1}.y,P'_{n-1}.z。 1.P0,...,Pn−1共n个点。满足相邻的点不重合。2.P0处各个轴关于弧长一阶导数也是已知的,设为P0′.x,P0′.y,P0′.z。3.Pn−1处各个轴关于弧长一阶导数也是已知的,设为Pn−1′.x,Pn−1′.y,Pn−1′.z。
要求依据上述条件求取每一段上以弧长为参数的曲线的三次参数方程。
分析:
对第 i 段三次样条函数而言,其形式必然为: 对 x i ( t ) : x i ( t ) = a x i + b x i t + c x i t 2 + d x i t 3 ; 0 < = t < L e n i ; 其中 L e n i 是此段终点到起点的距离。我们只需分别求出 a x i , b x i , c x i , d x i 即可。 对 y i ( t ) : y i ( t ) = a y i + b y i t + c y i t 2 + d y i t 3 ; 0 < = t < L e n i ; 其中 L e n i 是此段终点到起点的距离。我们只需分别求出 a y i , b y i , c y i , d y i 即可。 对 z i ( t ) : z i ( t ) = a z i + b z i t + c z i t 2 + d z i t 3 ; 0 < = t < L e n i ; 其中 L e n i 是此段终点到起点的距离。我们只需分别求出 a z i , b z i , c z i , d z i 即可。 我们一下仅分析 x i ( t ) 方程各个系数的求解, y i ( t ) , z i ( t ) 类似可得。 对第i段三次样条函数而言,其形式必然为:\\ 对x_{i}(t):\\ x_{i}(t) = ax_{i}+bx_{i}t+cx_{i}t^2+dx_{i}t^3; 0<=t<Len_{i};\\ 其中Len_{i}是此段终点到起点的距离。我们只需分别求出ax_{i},bx_{i},cx_{i},dx_{i}即可。\\ 对y_{i}(t):\\ y_{i}(t) = ay_{i}+by_{i}t+cy_{i}t^2+dy_{i}t^3; 0<=t<Len_{i};\\ 其中Len_{i}是此段终点到起点的距离。我们只需分别求出ay_{i},by_{i},cy_{i},dy_{i}即可。\\ 对z_{i}(t):\\ z_{i}(t) = az_{i}+bz_{i}t+cz_{i}t^2+dz_{i}t^3; 0<=t<Len_{i};\\ 其中Len_{i}是此段终点到起点的距离。我们只需分别求出az_{i},bz_{i},cz_{i},dz_{i}即可。\\ 我们一下仅分析x_{i}(t)方程各个系数的求解,y_{i}(t),z_{i}(t)类似可得。 对第i段三次样条函数而言,其形式必然为:对xi(t):xi(t)=axi+bxit+cxit2+dxit3;0<=t<Leni;其中Leni是此段终点到起点的距离。我们只需分别求出axi,bxi,cxi,dxi即可。对yi(t):yi(t)=ayi+byit+cyit2+dyit3;0<=t<Leni;其中Leni是此段终点到起点的距离。我们只需分别求出ayi,byi,cyi,dyi即可。对zi(t):zi(t)=azi+bzit+czit2+dzit3;0<=t<Leni;其中Leni是此段终点到起点的距离。我们只需分别求出azi,bzi,czi,dzi即可。我们一下仅分析xi(t)方程各个系数的求解,yi(t),zi(t)类似可得。
通过 x i ( 0 ) = P i . x = x i ; 可得: a x i = x i ; 通过x_{i}(0)=P_{i}.x=x_{i};可得:\\ ax_{i}=x_{i}; 通过xi(0)=Pi.x=xi;可得:axi=xi;
2.
通过 X i ( L e n i ) = x i + 1 ; 可得: b x i = ( x i + 1 − x i ) / L e n i − L e n i ∗ ( M i + 1 . x / 6 + M i . x / 3 ) ; 通过X_{i}(Len_{i})=x_{i+1};可得:\\ bx_{i}=(x_{i+1}-x_{i})/Len_{i}-Len_{i}*(M_{i+1}.x/6+M_{i}.x/3); 通过Xi(Leni)=xi+1;可得:bxi=(xi+1−xi)/Leni−Leni∗(Mi+1.x/6+Mi.x/3);
3.
通过 x i ′ ′ ( 0 ) = M i . x ; 可得: c x i = M i . x / 2 ; 通过x''_{i}(0)=M_{i}.x;可得:\\ cx_{i}=M_{i}.x/2; 通过xi′′(0)=Mi.x;可得:cxi=Mi.x/2;
4.
通过 x i ′ ′ ( L e n i ) = M i + 1 . x ; 可得: d x i = ( M i + 1 . x − M i . x ) / ( 6 ∗ L e n i ) ; 通过x''_{i}(Len_{i})=M_{i+1}.x;可得:\\ dx_{i}=(M_{i+1}.x-M_{i}.x)/(6*Len_{i}); 通过xi′′(Leni)=Mi+1.x;可得:dxi=(Mi+1.x−Mi.x)/(6∗Leni);
在上述我们假设已经知道:
n 个顶点处 x , y , z 关于弧长参数的二阶导数。记为 M i . x , M i . y , M i . z ; n个顶点处x,y,z关于弧长参数的二阶导数。记为M_{i}.x,M_{i}.y,M_{i}.z; n个顶点处x,y,z关于弧长参数的二阶导数。记为Mi.x,Mi.y,Mi.z;
下面分析各个顶点处各个轴关于弧长参数二阶导数的求取。
通过 X i ′ ( L e n i ) = x i + 1 ′ 0 ,可得: M i . x ∗ L e n i / 6 + M i + 1 . x ∗ ( L e n i + 1 + L e n i ) / 3 + M i + 2 . x ∗ ( L e n i + 1 / 6 ) = ( x i + 2 − x i + 1 ) / L e n i + 1 − ( x i + 1 − x i ) / L e n i ; 通过X'_{i}(Len_{i})=x'_{i+1}{0},可得:\\ M_{i}.x*Len_{i}/6+M_{i+1}.x*(Len_{i+1}+Len_{i})/3+M_{i+2}.x*(Len_{i+1}/6)=\\ (x_{i+2}-x_{i+1})/Len_{i+1}-(x_{i+1}-x_{i})/Len_{i}; 通过Xi′(Leni)=xi+1′0,可得:Mi.x∗Leni/6+Mi+1.x∗(Leni+1+Leni)/3+Mi+2.x∗(Leni+1/6)=(xi+2−xi+1)/Leni+1−(xi+1−xi)/Leni;
上述共可构成n-2个线性方程。为了求解n个自变量,我们还需要两个。
通过提供 x 0 ′ ( 0 ) ,可得: M 0 . x ∗ ( − L e n 0 / 3 ) + M 1 . x ∗ ( − L e n 0 / 6 ) = x 0 ′ ( 0 ) − ( x 1 − x 0 ) / L e n 0 ; 通过提供x'_{0}(0),可得:\\ M_{0}.x*(-Len_{0}/3)+M_{1}.x*(-Len_{0}/6)=x'_{0}(0)-(x_{1}-x_{0})/Len_{0}; 通过提供x0′(0),可得:M0.x∗(−Len0/3)+M1.x∗(−Len0/6)=x0′(0)−(x1−x0)/Len0;
3.
通过提供 x n − 2 ′ ( L e n n − 2 ) ,可得: M n − 2 . x ∗ ( L e n n − 2 / 6 ) + M n − 1 . x ∗ ( L e n n − 2 / 3 ) = x n − 2 ′ ( L e n n − 2 ) − ( x n − 1 − x n − 2 ) / L e n n − 2 ; 通过提供x'_{n-2}(Len_{n-2}),可得:\\ M_{n-2}.x*(Len_{n-2}/6)+M_{n-1}.x*(Len_{n-2}/3)=\\ x'_{n-2}(Len_{n-2})-(x_{n-1}-x_{n-2})/Len_{n-2}; 通过提供xn−2′(Lenn−2),可得:Mn−2.x∗(Lenn−2/6)+Mn−1.x∗(Lenn−2/3)=xn−2′(Lenn−2)−(xn−1−xn−2)/Lenn−2;
这样,我们构建了n个线性等式。这n个线性等式,可以用矩阵形式表示为:
A n , n M n , 1 = D n , 1 ; M n , 1 = A n , n − 1 D n , 1 ; A_{n,n}M_{n,1}=D_{n,1};\\ M_{n,1}=A^{-1}_{n,n}D_{n,1}; An,nMn,1=Dn,1;Mn,1=An,n−1Dn,1;
这样,我们通过先求取A的逆矩阵,接着便可求出M。然后依据前述求取系数的方法,便可唯一确定每一段x关于弧长的三次参数曲线方程。每一段y,z关于弧长的三次参数曲线方程类似可得。
相关文章:

三次插值曲线--插值技术
三次插值曲线 1.1.三次样条曲线 三次样条曲线的基本思想是,在给定的一系列点(称为控制点或数据点)之间,通过一系列三次多项式曲线段来拟合这些点,使得整个曲线既平滑又准确地通过所有控制点。 1.1.1.数学定义 给定…...
python循环结构
1.while 循环 语句: while 循环条件表达式: 代码块 else: 代码块 小练: 设计一百以内的偶数相加 n 0 while n < 100:n 1if n % 2 0 :print(n) 判断是不是闰年(四年一润和百年不润,或者四百年一润&am…...

深入理解Netty的Pipeline机制:原理与实践详解
深入理解Netty的Pipeline机制:原理与实践详解 Netty是一个基于Java的高性能异步事件驱动的网络应用框架,广泛应用于高并发网络编程。(学习netty请参考:深入浅出Netty:高性能网络应用框架的原理与实践)Nett…...
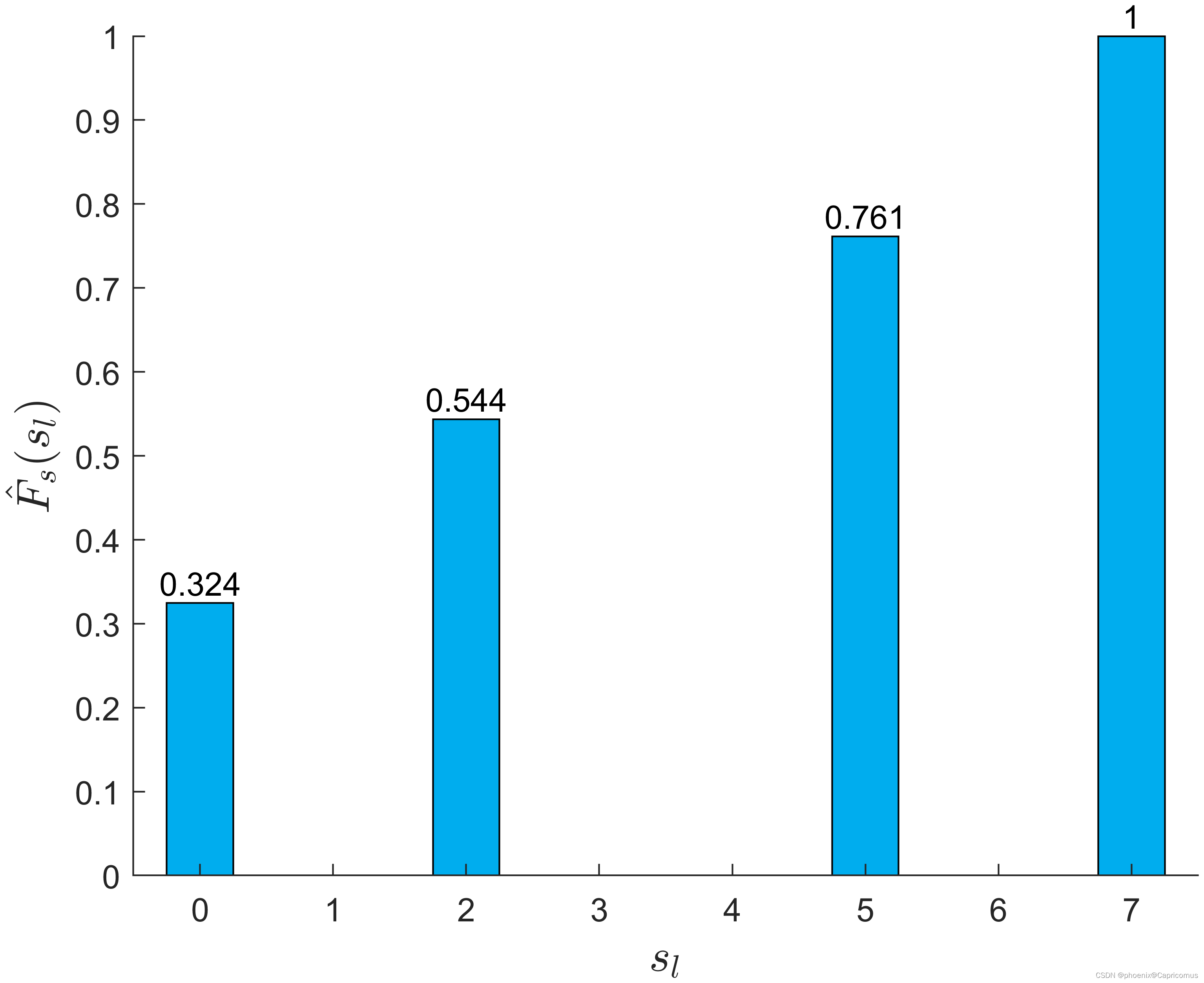
直方图均衡化示例
禹晶、肖创柏、廖庆敏《数字图像处理(面向新工科的电工电子信息基础课程系列教材)》 图3-17...

私域电商新纪元:消费增值模式的创新与成功实践
大家好,我是吴军,很高兴能够与您分享私域电商领域的魅力与机遇。今天,我将为大家呈现一个令人瞩目的成功案例,这个案例充分展现了私域电商的巨大潜力和无限可能。 在短短一个月的时间里,我们的客户成功实现了业绩的飞跃…...
Java——IO流(一)-(6/8):字节流-FileInputStream 每次读取多个字节(示例演示)、一次读取完全部字节(方式一、方式二,注意事项)
目录 文件字节输入流:每次读取多个字节 实例演示 注意事项 文件字节输入流:一次读取完全部字节 方式一 方式二 注意事项 文件字节输入流:每次读取多个字节 用到之前介绍过的常用方法: 实例演示 需求:用每次读取…...

服务器SSH 免密码登录
1. 背景 为了服务器的安全着想,设置的服务器密钥非常长。但是这导致每次连接服务器都需要输入一长串的密码,把人折腾的很痛苦,所以我就在想,能不能在终端SSH的时候无需输入密码。 windows 可以使用 xshell 软件,会自…...
Linux安装MySQL以及远程连接
1、Linux安装MySQL 1.1、准备解压包 MySQL5.x解压包 提取码:9y7n 1.2、通过rpm脚本安装 切记安装顺序:common --> libs --> client --> server 因为它们之间存在依赖关系,所以务必按照顺序安装 安装前请确保当前目录/文…...

SQL Server 数据库分页技术详解:选择最佳方法优化查询性能”。
当今数据驱动的应用程序中,数据库分页技术在优化查询性能和提升用户体验中扮演着重要角色。在 SQL Server 环境下,开发者面对大数据集时,常常需要选择合适的分页方法以平衡功能需求和性能优化。本文将详细介绍 SQL Server 中几种主要的分页技…...

electron录制-镜头缩放、移动
要求 1、当录屏过程中,鼠标点击,镜头应该往点击处拉近,等一段时间还原 2、录屏过程中,可能会发生多次点击,但是点击位置偏差大,可能会导致缩放之后,画面没出来,因此需要移动镜头帧 …...

红队内网攻防渗透:内网渗透之内网对抗:信息收集篇自动项目本机导出外部打点域内通讯PillagerBloodHound
红队内网攻防渗透 1. 内网自动化信息收集1.1 本机凭据收集类1.1.1、HackBrowserData 快速获取浏览器的账户密码1.1.2、Searchall 快速搜索服务器中的有关敏感信息还有浏览器的账户密码1.1.3、Pillager 适用于后渗透期间的信息收集工具,可以收集目标机器上敏感信息1.2 对外打点…...
2024最新IDEA插件开发+发布全流程 SelectCamelWords[选中驼峰单词](idea源代码)
2024最新IDEA插件开发(发布)-SelectCamelWords[选中驼峰单词](idea源代码) 参考文档 Jetbrains Idea插件开发文档: https://plugins.jetbrains.com/docs/intellij/welcome.html代码地址:https://github.com/yangfeng…...

【网络安全】网络安全基础精讲 - 网络安全入门第一篇
目录 一、网络安全基础 1.1网络安全定义 1.2网络系统安全 1.3网络信息安全 1.4网络安全的威胁 1.5网络安全的特征 二、入侵方式 2.1黑客 2.1.1黑客入侵方式 2.1.2系统的威胁 2.2 IP欺骗 2.2.1 TCP等IP欺骗 2.2.2 IP欺骗可行的原因 2.3 Sniffer探测 2.4端口扫描技术…...
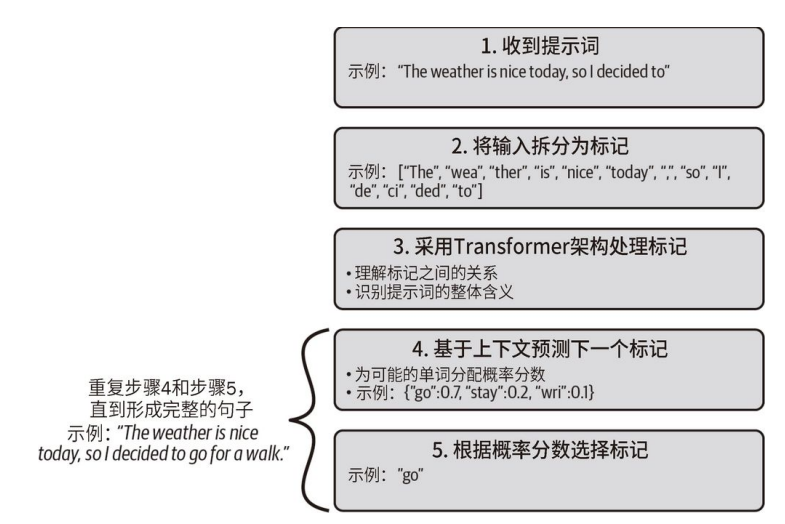
初识 GPT-4 和 ChatGPT
文章目录 LLM 概述理解 Transformer 架构及其在 LLM 中的作用解密 GPT 模型的标记化和预测步骤 想象这样⼀个世界:在这个世界里,你可以像和朋友聊天⼀样快速地与计算机交互。那会是怎样的体验?你可以创造出什么样的应用程序?这正是…...

【C语言】解决C语言报错:Array Index Out of Bounds
文章目录 简介什么是Array Index Out of BoundsArray Index Out of Bounds的常见原因如何检测和调试Array Index Out of Bounds解决Array Index Out of Bounds的最佳实践详细实例解析示例1:访问负索引示例2:访问超出上限的索引示例3:循环边界…...
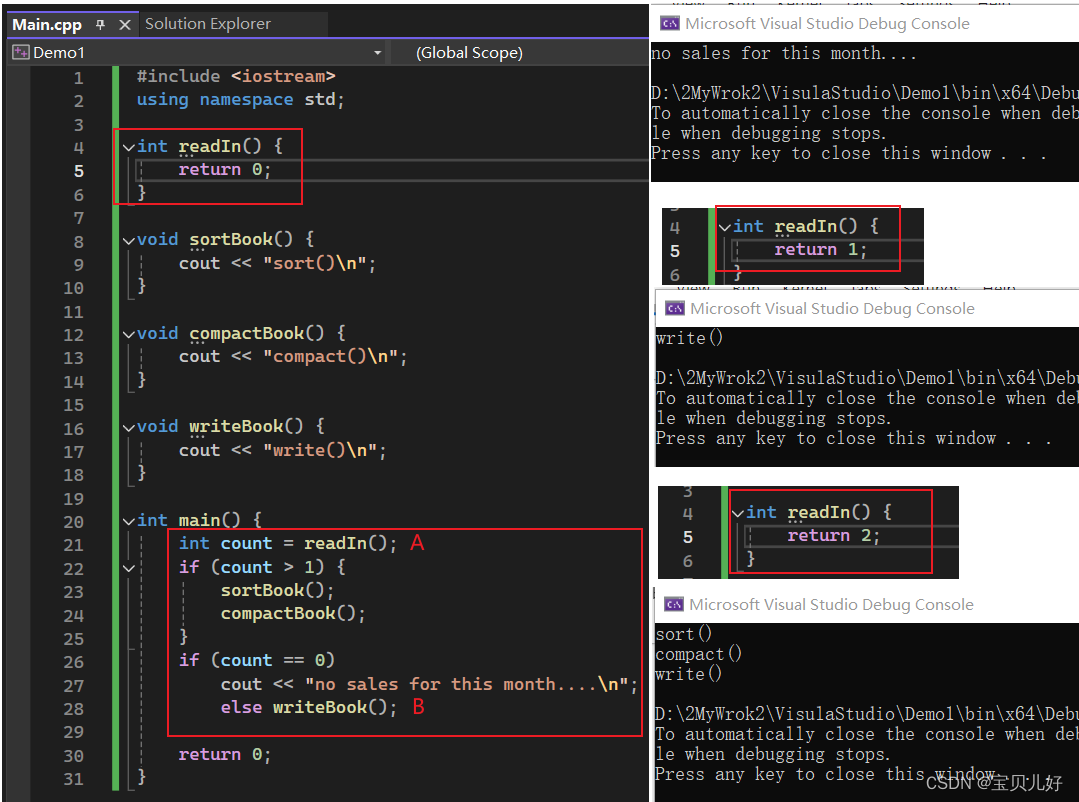
【C++】一个极简但完整的C++程序
一、一个极简但完整的C程序 我们编写程序是为了解决问题和任务的。 1、任务: 某个书店将每本售出的图书的书名和出版社,输入到一个文件中,这些信息以书售出的时间顺序输入,每两周店主会手工计算每本书的销售量、以及每个出版社的…...
)
Lua迭代器详解(附加红点功能实例)
Lua迭代器详解与用法 1. 什么是迭代器2. 为什么需要理解迭代器的原理3. 迭代器的实现0. 闭包1. 有状态迭代器2. 无状态迭代器 4. 红点树系统基础 1. 什么是迭代器 迭代器是一种能让我们遍历一个集合中的所有元素的代码结构。比如常用ipairs()和pairs()。 2. 为什么需要理解迭代…...

锂磷硫(LPS)属于硫化物固态电解质 Li7P3S11是代表性产品
锂磷硫(LPS)属于硫化物固态电解质 Li7P3S11是代表性产品 锂磷硫(LPS),为非晶态材料,是硫化物固态电解质代表性产品之一,具有热稳定性好、成本较低等优点,在固态电解质中离子电导率较…...

PointCloudLib 点云边缘点提取 C++版本
0.实现效果 1.算法原理 PCL(Point Cloud Library)中获取点云边界的算法主要基于点云数据的几何特征和法向量信息。以下是对该算法的详细解释,按照清晰的格式进行归纳: 算法概述 PCL中的点云边界提取算法主要用于从3D点云数据中识别并提取出位于物体边界上的点。这些边界…...

【Qt】QList<QVariantMap>中数据修改
1. 问题 QList<QVariantMap> 类型中,修改QVariantMap中的值。 2. 代码 //有效代码1QVariantMap itemMap itemList.at(0);itemMap.insert("title", "test");itemList.replace(0, itemMap);//有效代码 2itemList.operator [](0).insert(…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
