【IC验证】UVM实验lab03
1. TLM端口的创建、例化与使用
创建:
uvm_get_blocking_port #(fmt_trans) mon_bp_port;例化:
function new(string name = "mcdf_refmod", uvm_component parent);super.new(name, parent);fmt_trans = new("fmt_trans", this);
endfunction传入数据:
this.mon_bp_port.put(t);取出数据:
this.mon_bp_port.get(t);连接:
2. 多向通信
宏声明:
'uvm_blocking_put_imp_decl(_chnl0);端口创建:
uvm_blocking_put_imp_chnl0 #(data, component_name) chnl0_bp_imp;例化:
chnl0_bp_imp = mew("chnl0_bp_imp", this);3. 回调函数的使用
定义callback:
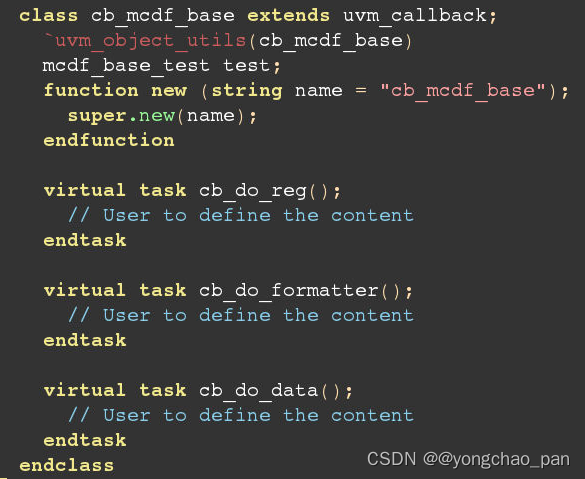
将callback与组件绑定:
对于后续继承于mcdf_base_test的所有子类,例如cb_mcdf_data_consistence_basic_test都不需要再做这个绑定了


在该组件里面插入callback:
在mcdf_base_test里面调用cb_mcdf_base的cb_do_reg方法。相当于是在这里预留了一个修改入口,方便后续继承该类,并对callback里面的方法进行修改

对cb里面的方法进行修改实现:

对callback进行例化添加使用:

相关文章:

【IC验证】UVM实验lab03
1. TLM端口的创建、例化与使用 创建: uvm_get_blocking_port #(fmt_trans) mon_bp_port; 例化: function new(string name "mcdf_refmod", uvm_component parent);super.new(name, parent);fmt_trans new("fmt_trans", this);…...
方法总结)
document.write()方法总结
document.write()方法总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!document.write()方法是JavaScript中用于向HTML文档写入内容的方法之一。它允许我们在…...

C#循环语句总结
前言 正所谓磨刀不误砍柴工,C#上位机软件开发能力的提升离不开对C#语法的精通,本文接着讲解C#语法知识中的循环语句,在C#程序开发中我们经常会用到各种循环语句,常见的有for循环、while循环,本文就是对C#中用到的各种…...

Spring-bean
Spring 网站:spring.io 两个方面: 简化开发: IoCAOP 框架整合: MyBatis SpringFrameWork系统架构(上层依赖下层) 解决问题(代码耦合度高——模块与模块之间的依赖程度) 目标&am…...
Linux常用命令(14)—查看文件内容(有相关截图)
写在前面: 最近在学习Linux命令,记录一下学习Linux常用命令的过程,方便以后复习。仅供参考,若有不当的地方,恳请指正。如果对你有帮助,欢迎点赞,关注,收藏,评论…...

【html】用html+css实现银行的账户信息表格
我们先来看一看某银行的账户信息表格 我们自己也可以实现类似的效果 效果图: 大家可以看到,其实效果差不多 接下来看看我们实现的代码 源码: <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"&…...

两种单例模式(保证线程安全)
开始前,球球各位读者给个三连吧,有错误感谢指出,谢谢 单例模式也叫单个实例,也就是这个类只有且只能有一个实例对象,这样一个类就叫做“单例”;单例模式有很多种,这里只介绍“饿汉模式”和“懒…...

开发 Golang 项目的 Docker 化案例
开发 Golang 项目的 Docker 化案例 在这个案例中,我们将展示如何使用 Docker 容器化一个简单的 Golang Web 应用。我们将创建一个基于 Go 的 Hello World 应用,并使用 Docker 和 Docker Compose 管理容器化环境。 1. 创建 Golang Web 应用 首先&#…...

PHP面试宝典之Laravel篇
Laravel简介 Laravel是一种优雅的PHP Web应用程序框架,它具有简洁、优雅的语法,并提供了强大的工具用于构建大型、健壮的应用程序。Laravel采用了现代PHP开发的最佳实践,因此深受开发者欢迎。 Laravel面试常见问题 1. 什么是Laravel中间件…...
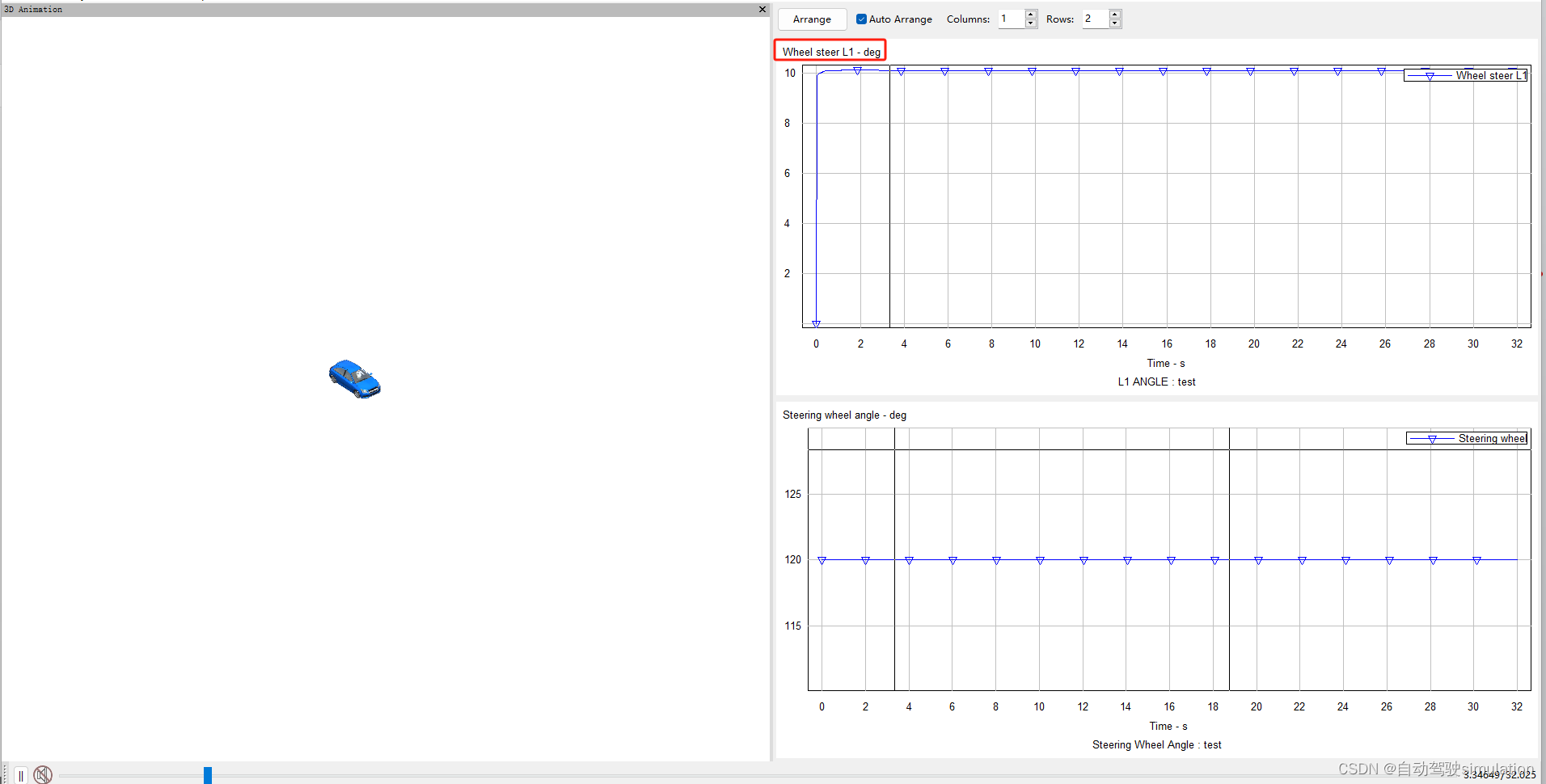
自动驾驶仿真:Carsim转向传动比设置
文章目录 一、转向传动比概念二、设置转向传动比1、C factor概念2、Steer Kinematics概念3、传动比计算公式 三、转向传动比验证 一、转向传动比概念 转向传动比(Steering Ratio)表示方向盘转动角度与车轮转动角度之间的关系。公式如下: 转向…...
 交叉熵损失函数详解和要点提醒)
PyTorch nn.CrossEntropyLoss() 交叉熵损失函数详解和要点提醒
文章目录 前置知识nn.CrossEntropyLoss() 交叉熵损失参数数学公式带权重的公式(weight)标签平滑(label_smoothing) 要点 附录参考链接 前置知识 深度学习:关于损失函数的一些前置知识(PyTorch Loss&#x…...

DW学习笔记|数学建模task2
本章主要涉及到的知识点有: 微分方程的解法如何用 Python 解微分方程偏微分方程及其求解方法微分方程的基本案例差分方程的求解数值计算方法元胞自动机 2.1 微分方程的理论基础 微分方程是什么?如果你参加过高考,可能在高三备考中遇到过这…...
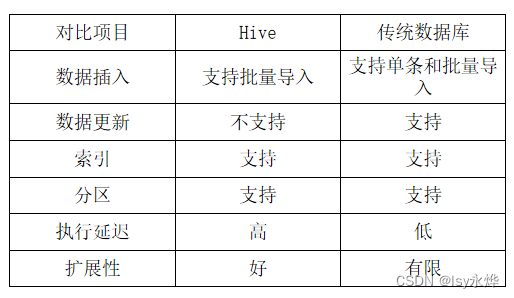
【大数据 复习】第9章 数据仓库分析工具Hive
一、概念 1.概述 (1)Hive是一个构建于Hadoop顶层的数据仓库工具。 (2)某种程度上可以看作是用户编程接口,本身不存储和处理数据。 (3)依赖分布式文件系统HDFS存储数据。 (4…...
ionic7 从安装 到 项目启动最后打包成 apk
报错处理 在打包的时候遇到过几个问题,这里记录下来两个 Visual Studio Code运行ionic build出错显示ionic : 无法加载文件 ionic 项目通过 android studio 打开报错 capacitor.settings.gradle 文件不存在 说明 由于之前使用的是 ionic 3,当时打包的…...
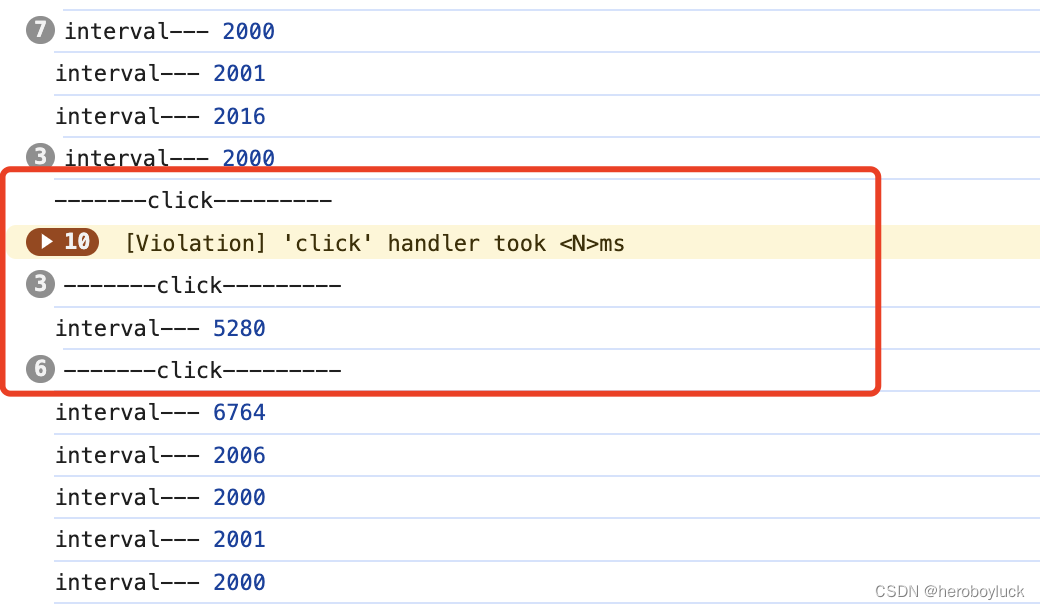
setInterval 定时任务执行时间不准验证
一般在处理定时任务的时候都使用setInterval间隔定时调用任务。 setInterval(() > {console.log("interval"); }, 2 * 1000);我们定义的是两秒执行一次,但是浏览器实际执行的间隔时间只多不少。这是由于浏览器执行 JS 是单线程模式,使用se…...

Stable Diffusion Model网站
Civitai Models | Discover Free Stable Diffusion Modelshttps://www.tjsky.net/tutorial/488https://zhuanlan.zhihu.com/p/610298913超详细的 Stable Diffusion ComfyUI 基础教程(一):安装与常用插件 - 优设网 - 学设计上优设 (uisdc.com)…...
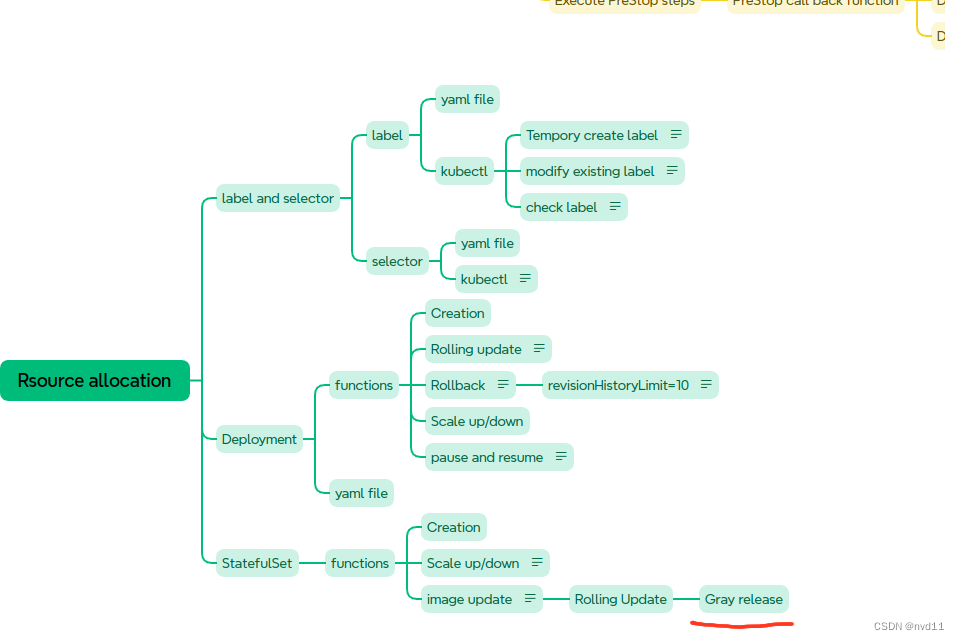
K8S - 实现statefulset 有状态service的灰度发布
什么是灰度发布 Canary Release 参考 理解 什么是 滚动更新,蓝绿部署,灰度发布 以及它们的区别 配置partition in updateStrategy/rollingUpdate 这次我为修改了 statefulset 的1个yaml file statefulsets/stateful-nginx-without-pvc.yaml: --- apiVe…...

Qt 技术博客:深入理解 Qt 中的 delete 和 deleteLater 与信号槽机制
在 Qt 开发中,内存管理和对象生命周期的处理是至关重要的一环。特别是在涉及信号和槽机制时,如何正确删除对象会直接影响应用程序的稳定性。本文将详细讨论在使用 Qt 的信号和槽机制时,delete 和 deleteLater 的工作原理,并给出最…...
自学鸿蒙HarmonyOS的ArkTS语言<一>基本语法
一、一个ArkTs的目录结构 二、一个页面的结构 A、装饰器 Entry 装饰器 : 标记组件为入口组件,一个页面由多个自定义组件组成,但是只能有一个组件被标记 Component : 自定义组件, 仅能装饰struct关键字声明的数据结构 State:组件中的状态变量…...
)】)
【OpenGauss源码学习 —— (ALTER TABLE(列存修改列类型))】
ALTER TABLE(列存修改列类型) ATExecAlterColumnType 函数1. 检查和处理列存储表的字符集:2. 处理自动递增列的数据类型检查:3. 处理生成列的类型转换检查:4. 处理生成列的数据类型转换: build_column_defa…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
