代码随想录算法训练营Day46|动态规划:121.买卖股票的最佳时机I、122.买卖股票的最佳时机II、123.买卖股票的最佳时机III
买卖股票的最佳时机I
121. 买卖股票的最佳时机 - 力扣(LeetCode)
之前用贪心算法做过相同的题,这次考虑使用动态规划来完成。
dp[i]表示前i天的最大利润
我们已知每一天的价格price[i],则dp[i]为每一天的价格price[i]减去当初购买的价格buyprice与dp1[i-1]的较大值。 dp[i] = max(dp[i-1],price[i]-buyprice)。
dp[0]表示收益为0
从前往后递推,注意要更新buyprice的价格为当前遍历过的数据中最小的值。
最后返回dp[price.size()-1]。
其实和贪心差不多,或者说贪心是这里动态规划的变体?
class Solution {
public:int maxProfit(vector<int>& prices) {// 如果价格数组为空,则没有利润,返回0if(prices.size()==0)return 0;// 初始化买入价格为第一天的价格int buyprice = prices[0];// 创建一个动态数组dp,用于存储到第i天为止的最大利润// 初始化dp[0]为0,因为第一天买入卖出没有利润vector<int>dp(prices.size(),0);dp[0] = 0;// 遍历价格数组,从第二天开始for(int i = 1;i < prices.size();i++){// 更新买入价格为当前价格和之前最低价格中的较小值buyprice = min(buyprice,prices[i]);// 计算如果在今天卖出股票能获得的最大利润// 即取当前价格减去最低买入价格和前一天的最大利润中的较大值dp[i] = max(dp[i-1],prices[i]-buyprice);}// 返回最后一天的最大利润,即整个期间的最大利润return dp[prices.size()-1];}
};
算法的时间复杂度为O(n),遍历一次数组,空间复杂度同样为O(n),需要维护一个dp数组。
买卖股票的最佳时机II
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
由于不能同时参与多笔交易,则每天结束,只会存在拥有一支股票和无股票两种情况,由次,创建一个二维的dp数组(n*2的大小),其中dp[i][0]表示当天结束时,手头没有股票的最大利润,dp[i][1]表示当天结束时手头有股票的利润。
考虑推导,手头没有股票有两种情况,一是前一天就没有股票且今天没买,二是前一天有股票,但今天卖了,则dp[i][0] = max(dp[i-1][0],dp[i-1][1]+price[i]),手头有股票同样有两种情况,一是前一天没有股票但今天买了,二是昨天的股票没卖。
dp[i][1] = max(dp[i-1][0] - price[i],dp[i-1][1])
考虑到这样的情况,需对dp[0][0]和dp[1][0]初始化,dp[0][0] = 0,dp[0][1]=-price[0]
从前往后遍历(本质上还是从天来推导)
最后一天由于dp[i][0]一定大于dp[i][1],返回dp[i][0]即可。
class Solution {
public:int maxProfit(vector<int>& prices) {// 创建一个二维数组dp,行数为prices的大小,列数为2// dp[i][0]代表第i天结束时,不持有股票的最大利润// dp[i][1]代表第i天结束时,持有股票的最大利润vector<vector<int>> dp(prices.size(), vector<int>(2, 0));// 初始化dp数组的第一行// 第一天不持有股票的最大利润为0dp[0][0] = 0; // 第一天持有股票的最大利润为负的第一天价格(即买入股票)dp[0][1] = -prices[0];// 遍历价格数组,从第二天开始更新dp数组for(int i = 1; i < prices.size(); i++){// 更新第i天不持有股票的最大利润// 可以是前一天就不持有股票,或者前一天持有股票但今天卖出dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);// 更新第i天持有股票的最大利润// 可以是前一天就持有股票,或者前一天不持有股票但今天买入dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1]);}// 返回最后一天不持有股票的最大利润return dp[prices.size()-1][0];}
};算法的时间复杂度为O(n),空间复杂度为O(n)。
买卖股票的最佳时机III
123. 买卖股票的最佳时机 III - 力扣(LeetCode)
每天结束后,我们手中持有的股票有以下五种情况。
- 无操作
- 第一次买操作
- 完成一笔操作
- 第二次买操作
- 完全两笔交易
由此,我们根据买卖股票的最佳时机II相似的方式,来完成本题。
-
dp[i][0]:没有进行任何交易时的利润。 -
dp[i][1]:进行了第一次买入后的利润。 -
dp[i][2]:完成了第一次卖出后的利润。 -
dp[i][3]:进行了第二次买入后的利润。 -
dp[i][4]:完成了第二次卖出后的利润。
dp[i][0]始终为0,这里我们将dp[i][0] = do[i-1][0];
dp[i][1] = max(dp[i-1][1],dp[i-1][0] - prices[i])
dp[i][2] = max(dp[i-1][2],dp[i-1][1] + prices[i])
dp[i][3] = max(dp[i-1][3],dp[i-1][2] - prices[i])
dp[i][4] = max(dp[i-1][4],dp[i-1][3] + prices[i])
从前向后遍历
返回dp[prices.size()-1][4]
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0; // 如果没有价格数据,则利润为0vector<vector<int>> dp(prices.size(), vector<int>(5, 0)); // 初始化dp数组// 初始化第一天的状态dp[0][1] = -prices[0]; // 第一天买入股票后的利润dp[0][3] = -prices[0]; // 假设k>=2,第一天买入第二次股票后的利润for (int i = 1; i < prices.size(); i++) { // 遍历价格数组// 更新第i天不进行任何交易的最大利润,这个值始终为0,因为不交易不会有利润变化dp[i][0] = dp[i - 1][0];// 更新第i天进行第一次买入后的最大利润dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);// 更新第i天完成第一次卖出后的最大利润dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);// 更新第i天进行第二次买入后的最大利润dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);// 更新第i天完成第二次卖出后的最大利润dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}// 返回最后一天完成所有交易后的最大利润return dp[prices.size() - 1][4];}
};
算法的时间复杂度为O(n),空间复杂度为O(n)。
相关文章:

代码随想录算法训练营Day46|动态规划:121.买卖股票的最佳时机I、122.买卖股票的最佳时机II、123.买卖股票的最佳时机III
买卖股票的最佳时机I 121. 买卖股票的最佳时机 - 力扣(LeetCode) 之前用贪心算法做过相同的题,这次考虑使用动态规划来完成。 dp[i]表示前i天的最大利润 我们已知每一天的价格price[i],则dp[i]为每一天的价格price[i]减去当初…...

hive on spark 记录
环境: hadoop 2.7.2 spark-without-hadoop 2.4.6 hive 2.3.4 hive-site.xml <property><name>hive.execution.engine</name><value>spark</value> </property> <property><name>spark.yarn.jars</name>&l…...
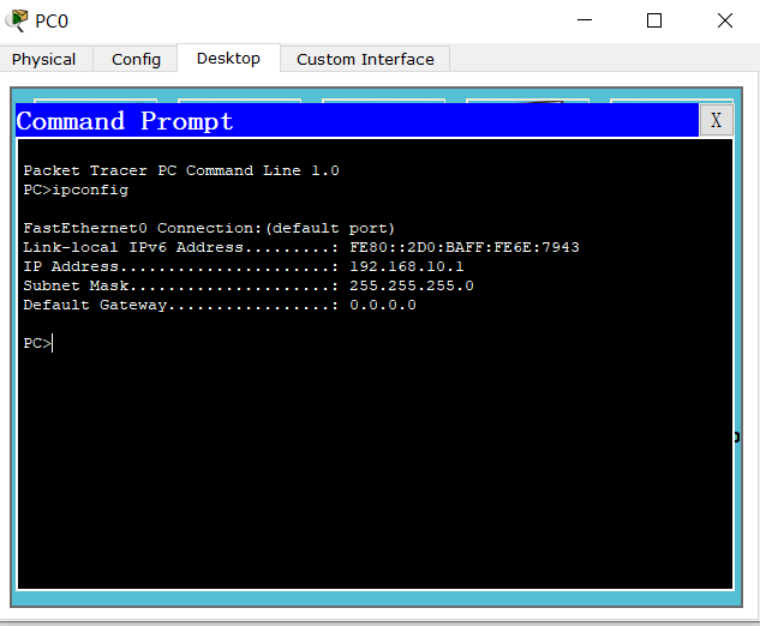
【计算机网络体系结构】计算机网络体系结构实验-DHCP实验
服务器ip地址 2. 服务器地址池 3. 客户端ip 4. ping Ipconfig...

攻防世界-pdf
方法一:打开是pdf格式的文件,里面有一张图,题目提示图下面什么都没有?emmm用chrom打开pdf——ctrlf搜索flag,里面是有东西的,ctrla复制就可以了。 方法二:题目提示图下面什么都没有,…...

关于后端幂等性问题分析与总结
后端幂等性(Idempotency)是指对系统执行一次操作或多次执行相同的操作,其结果始终如一。在分布式系统和API设计中,这是一个关键概念,因为它能保证用户无论请求被路由到哪个节点,多次执行相同的请求都不会导…...

2024广东省职业技能大赛云计算赛项实战——容器云平台搭建
容器云平台搭建 前言 容器镜像使用的是斗学培训平台提供的镜像包,这东西网上都没有,一堆人要,我是靠自己想的方法获取到了,也不敢给。你们可以通过在这个网站申请环境进行操作https://ncc.douxuedu.com/ 虚拟机使用的是自行创建…...

手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发
手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发 专业版 插件版 手持弹幕小程序通常提供多种功能,以便用户在不同的场合如夜店、表白、接机等使用。以下是一些常见的功能列表: 文本输入: 输入要显示的文字内容,…...

红队内网攻防渗透:内网渗透之内网对抗:代理通讯篇无外网或不可达SockS全协议规则配置C2正反向上线解决方案
红队内网攻防渗透 1. 内网代理通讯1.1 网络不可达实战环境模拟1.1.1 CS代理技术-SockS配置-网络不可达-通讯解决1.1.1.1 反向shell上线入口点主机1.1.1.2 入口点CS搭建sokcs4代理1.1.1.3 本地使用Proxifier访问代理1.1.1 CS代理技术-正反向监听-网络不可达-C2上线1.1.1.4 正向s…...

PHP学习总结-入门篇
PHP简介 PHP (Hypertext Preprocessor),即“超文本预处理器”。PHP 是一种创建动态交互性站点的强有力的服务器端脚本语言。PHP语法吸收了C语言、Java和Perl的特点,便于学习。PHP 是开源免费的,主要适用于Web开发领域,使用广泛。…...
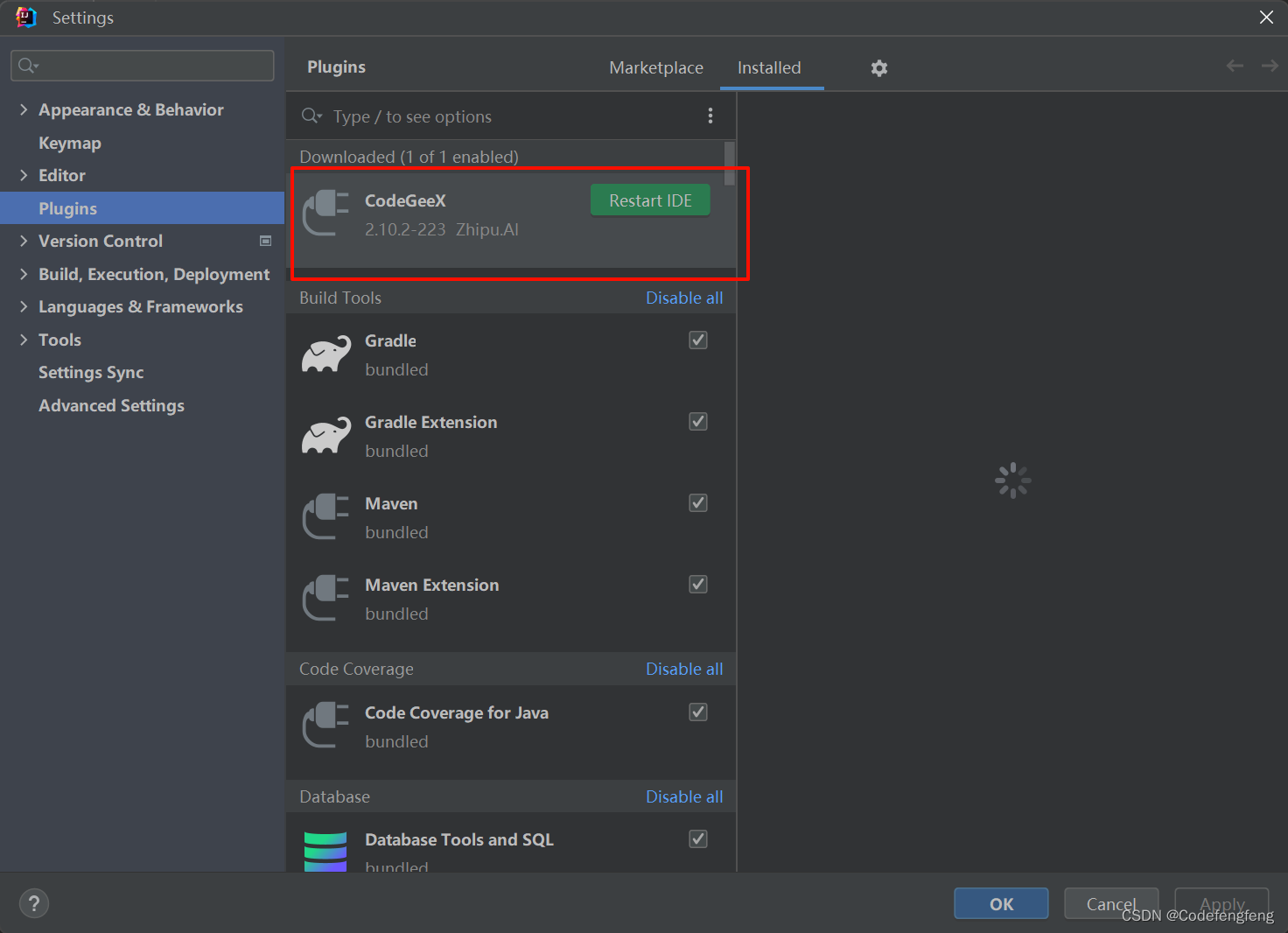
IDEA Plugins中搜索不到插件解决办法
IDEA中搜不到插件有三种解决方案: 设置HTTP选项,可以通过File->Settings->Plugins->⚙->HTTP Proxy Settings进行设置 具体可参考这篇博文:IDEA Plugins中搜索不到插件解决办法本地安装,ile->Settings->Plugin…...
SpringBootWeb 篇-入门了解 Vue 前端工程的创建与基本使用
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 基于脚手架创建前端工程 1.1 基于 Vue 开发前端项目的环境要求 1.2 前端工程创建的方式 1.2.1 基于命令的方式来创建前端工程 1.2.2 使用图形化来创建前端工程 1.…...
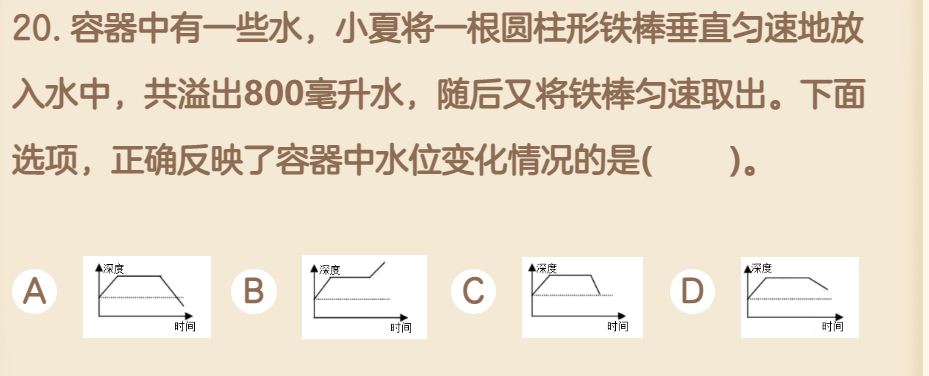
折线统计图 初级
此为折线统计图的初级题目。 本次的题目较难,菜鸡请退出。 4. 下图显示了甲、乙两台电脑的价格以及它们已使用的年数,从图中可以知道( )。 15. 妈妈去菜市场买菜,走到半路遇到一位熟人聊了一会儿,突然发现忘了带钱。于是马上回…...

最新下载:XmanagerXShell【软件附加安装教程】
相信大家都认同支持IPv6:最近越来越多的公司和国家都采用了IPv6,Xmanager的最新版本v5也加入支持这个功能,无论你是同时使用IPv4和IPv6网络或者完全的IPv6网络,Xmanager 5都可完全满足你的要求,使用MIT Kerberos认证…...
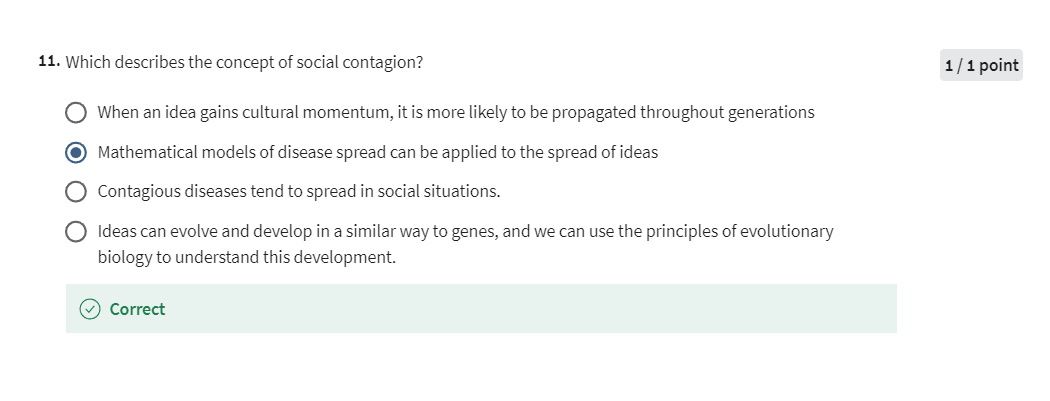
Coursera耶鲁大学金融课程:Financial Markets 笔记Week 02
Financial Markets 本文是学习 https://www.coursera.org/learn/financial-markets-global这门课的学习笔记 这门课的老师是耶鲁大学的Robert Shiller https://en.wikipedia.org/wiki/Robert_J._Shiller Robert James Shiller (born March 29, 1946)[4] is an American econom…...

读书笔记:《生死疲劳》
《生死疲劳》. 莫言 生死疲劳》是莫言最重要的代表作之一。他用动物的视角、俏皮的语言和鬼才的叙事手法,使这本讲述沉重故事的书中处处充满惊喜;用幽默、戏谑的方式化解现实的痛苦,让人在痛苦时依旧能笑出声来,给人以力量。…...

C++面向对象三大特性--多态
C面向对象三大特性–多态 文章目录 C面向对象三大特性--多态1.虚函数(Virtual Function)2.纯虚函数(Pure Virtual Function)和抽象类(Abstract Class)3.重写(Override)4.动态绑定&am…...

啥移动硬盘格式能更好兼容Windows和Mac系统 NTFS格式苹果电脑不能修改 paragon ntfs for mac激活码
对于同时使用Windows和Mac操作系统的用户而言,选择一个既能确保数据互通又能满足大容量存储需求的移动硬盘格式尤为重要。下面我们来看看啥移动硬盘格式能更好兼容Windows和Mac系统,NTFS格式苹果电脑不能修改的相关内容。 一、啥移动硬盘格式能更好兼容…...

【面试】i++与++i的区别
目录 1. 情况11.1 i1.2 i 2. 情况23. 情况34. 情况4 1. 情况1 1.1 i 1.代码块 public void test(){int i 10;i;System.out.println(i);}2.字节码 0 bipush 102 istore_13 iinc 1 by 16 getstatic #2 <java/lang/System.out : Ljava/io/PrintStream;>9 iload_1 10 inv…...

使用 devtool 本地调试 nodejs
安装 # 全局安装 $ npm install devtool -g # 或临时安装 $ npx devtool [file] [opts]用法 Usage:devtool [入口文件] [opts]Options:--watch, -w enable file watching (for development) # 动态检测文件变更,不用每次手动重启--quit, -q …...
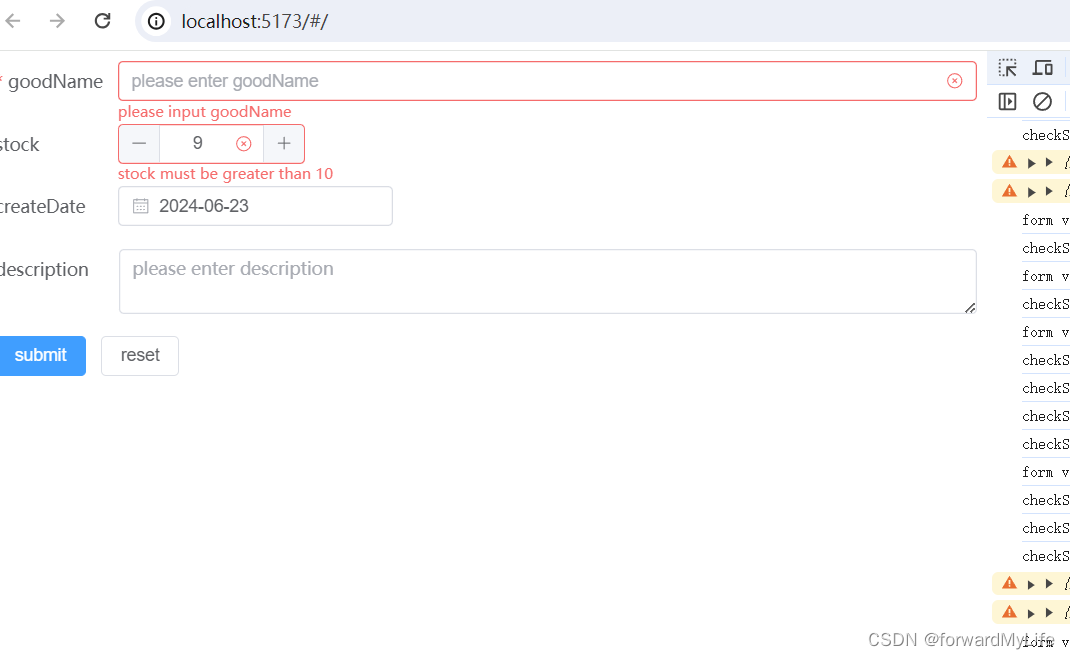
element-plus 表单组件 之element-form
elment-plus的表单组件的标签有el-form,el-form-item。 单个el-form标签内包裹若干个el-form-item,el-form-item包裹具体的表单组件,如输入框组件,多选组件,日期组件等。 el-form组件的主要作用是:提供统一的布局给其他表单组件&…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
