手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发

手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发
专业版
插件版
手持弹幕小程序通常提供多种功能,以便用户在不同的场合如夜店、表白、接机等使用。以下是一些常见的功能列表:
-
文本输入:
- 输入要显示的文字内容,支持多行输入。
- 可能有限制字数,确保屏幕滚动时的可读性。
-
滚动速度:
- 调整文字滚动的速度,从慢速到快速。
-
字体样式:
- 选择字体类型,如宋体、黑体等。
- 改变字体大小,以适应不同的视觉需求。
-
颜色定制:
- 自定义文字颜色,可以选择各种颜色或预设主题色。
- 背景颜色可调,以增加对比度和视觉效果。
-
动画效果:
- 不同的滚动方式,如平移、淡入淡出、闪烁等。
- 可能包含3D滚动效果或波浪滚动等特殊效果。
-
亮度控制:
- 调节屏幕亮度,适应不同环境光线。
-
模式选择:
- 提供多种场景模式,如表白模式、接机模式等,预设适合的字体、颜色和速度组合。
-
保存与分享:
- 可保存自定义的设置,方便下次使用。
- 分享设置给朋友,或直接分享生成的弹幕图片到社交媒体如微信、抖音。
-
手电筒集成:
- 在某些应用中,可能结合手机的手电筒功能,实现亮光背景的LED效果。
-
自定义背景图片:
- 有些小程序允许上传背景图片,增加个性化元素。
-
定时关闭:
- 设置定时器,自动停止显示弹幕。
请记住,具体的功能可能会因不同的手持弹幕小程序而略有差异,用户在实际使用时应以小程序内的实际功能为准。
相关文章:

手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发
手持弹幕LED滚动字幕屏夜店表白手灯接机微信抖音小程序开源版开发 专业版 插件版 手持弹幕小程序通常提供多种功能,以便用户在不同的场合如夜店、表白、接机等使用。以下是一些常见的功能列表: 文本输入: 输入要显示的文字内容,…...

红队内网攻防渗透:内网渗透之内网对抗:代理通讯篇无外网或不可达SockS全协议规则配置C2正反向上线解决方案
红队内网攻防渗透 1. 内网代理通讯1.1 网络不可达实战环境模拟1.1.1 CS代理技术-SockS配置-网络不可达-通讯解决1.1.1.1 反向shell上线入口点主机1.1.1.2 入口点CS搭建sokcs4代理1.1.1.3 本地使用Proxifier访问代理1.1.1 CS代理技术-正反向监听-网络不可达-C2上线1.1.1.4 正向s…...

PHP学习总结-入门篇
PHP简介 PHP (Hypertext Preprocessor),即“超文本预处理器”。PHP 是一种创建动态交互性站点的强有力的服务器端脚本语言。PHP语法吸收了C语言、Java和Perl的特点,便于学习。PHP 是开源免费的,主要适用于Web开发领域,使用广泛。…...
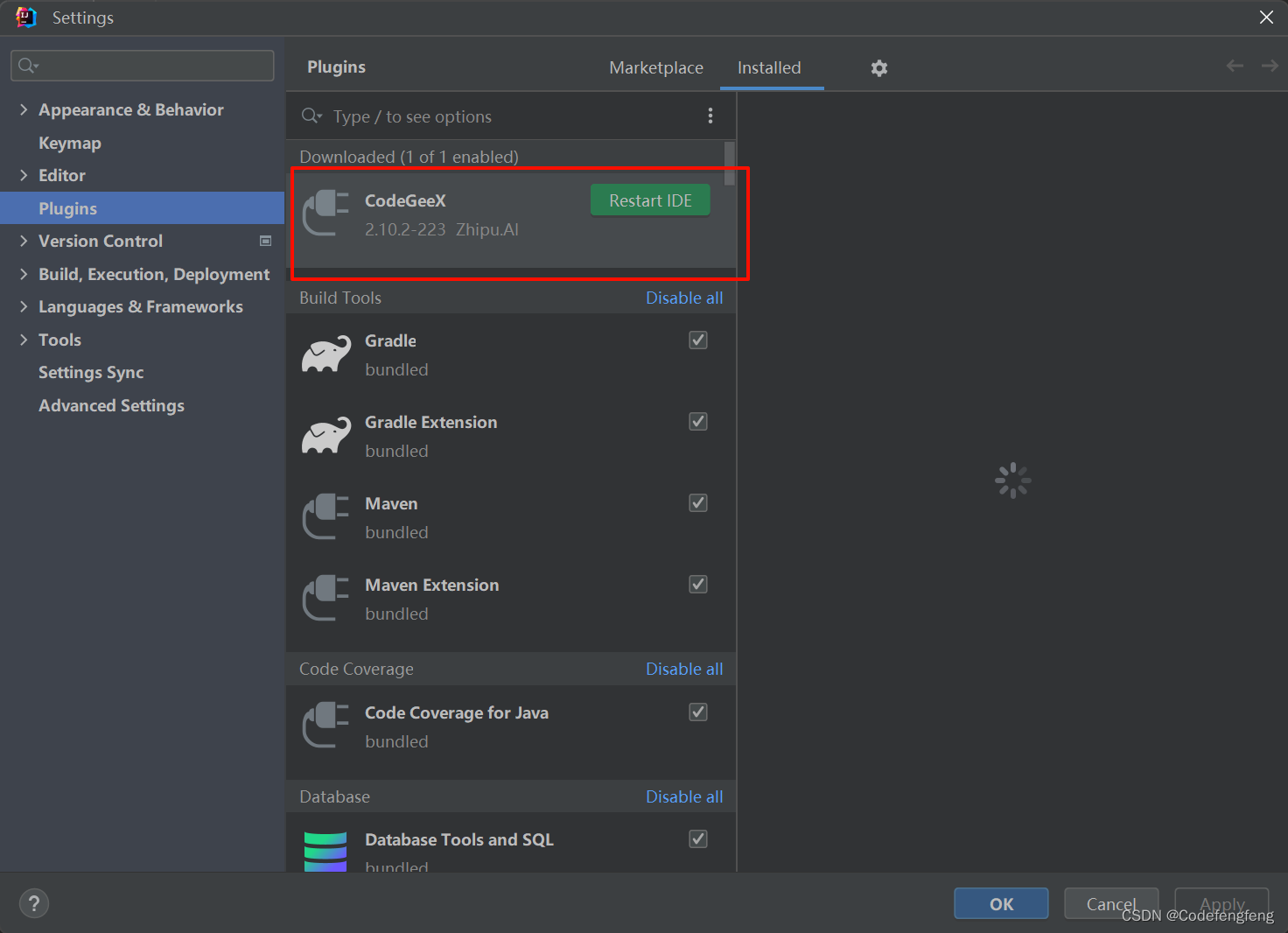
IDEA Plugins中搜索不到插件解决办法
IDEA中搜不到插件有三种解决方案: 设置HTTP选项,可以通过File->Settings->Plugins->⚙->HTTP Proxy Settings进行设置 具体可参考这篇博文:IDEA Plugins中搜索不到插件解决办法本地安装,ile->Settings->Plugin…...
SpringBootWeb 篇-入门了解 Vue 前端工程的创建与基本使用
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 基于脚手架创建前端工程 1.1 基于 Vue 开发前端项目的环境要求 1.2 前端工程创建的方式 1.2.1 基于命令的方式来创建前端工程 1.2.2 使用图形化来创建前端工程 1.…...
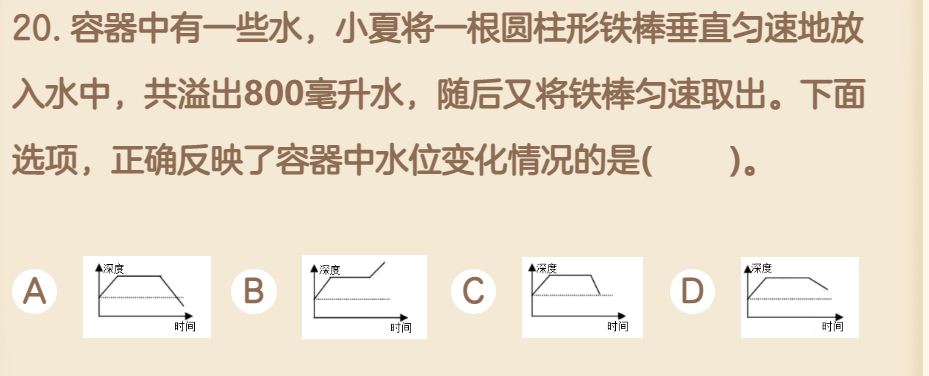
折线统计图 初级
此为折线统计图的初级题目。 本次的题目较难,菜鸡请退出。 4. 下图显示了甲、乙两台电脑的价格以及它们已使用的年数,从图中可以知道( )。 15. 妈妈去菜市场买菜,走到半路遇到一位熟人聊了一会儿,突然发现忘了带钱。于是马上回…...

最新下载:XmanagerXShell【软件附加安装教程】
相信大家都认同支持IPv6:最近越来越多的公司和国家都采用了IPv6,Xmanager的最新版本v5也加入支持这个功能,无论你是同时使用IPv4和IPv6网络或者完全的IPv6网络,Xmanager 5都可完全满足你的要求,使用MIT Kerberos认证…...
Coursera耶鲁大学金融课程:Financial Markets 笔记Week 02
Financial Markets 本文是学习 https://www.coursera.org/learn/financial-markets-global这门课的学习笔记 这门课的老师是耶鲁大学的Robert Shiller https://en.wikipedia.org/wiki/Robert_J._Shiller Robert James Shiller (born March 29, 1946)[4] is an American econom…...

读书笔记:《生死疲劳》
《生死疲劳》. 莫言 生死疲劳》是莫言最重要的代表作之一。他用动物的视角、俏皮的语言和鬼才的叙事手法,使这本讲述沉重故事的书中处处充满惊喜;用幽默、戏谑的方式化解现实的痛苦,让人在痛苦时依旧能笑出声来,给人以力量。…...

C++面向对象三大特性--多态
C面向对象三大特性–多态 文章目录 C面向对象三大特性--多态1.虚函数(Virtual Function)2.纯虚函数(Pure Virtual Function)和抽象类(Abstract Class)3.重写(Override)4.动态绑定&am…...

啥移动硬盘格式能更好兼容Windows和Mac系统 NTFS格式苹果电脑不能修改 paragon ntfs for mac激活码
对于同时使用Windows和Mac操作系统的用户而言,选择一个既能确保数据互通又能满足大容量存储需求的移动硬盘格式尤为重要。下面我们来看看啥移动硬盘格式能更好兼容Windows和Mac系统,NTFS格式苹果电脑不能修改的相关内容。 一、啥移动硬盘格式能更好兼容…...

【面试】i++与++i的区别
目录 1. 情况11.1 i1.2 i 2. 情况23. 情况34. 情况4 1. 情况1 1.1 i 1.代码块 public void test(){int i 10;i;System.out.println(i);}2.字节码 0 bipush 102 istore_13 iinc 1 by 16 getstatic #2 <java/lang/System.out : Ljava/io/PrintStream;>9 iload_1 10 inv…...

使用 devtool 本地调试 nodejs
安装 # 全局安装 $ npm install devtool -g # 或临时安装 $ npx devtool [file] [opts]用法 Usage:devtool [入口文件] [opts]Options:--watch, -w enable file watching (for development) # 动态检测文件变更,不用每次手动重启--quit, -q …...
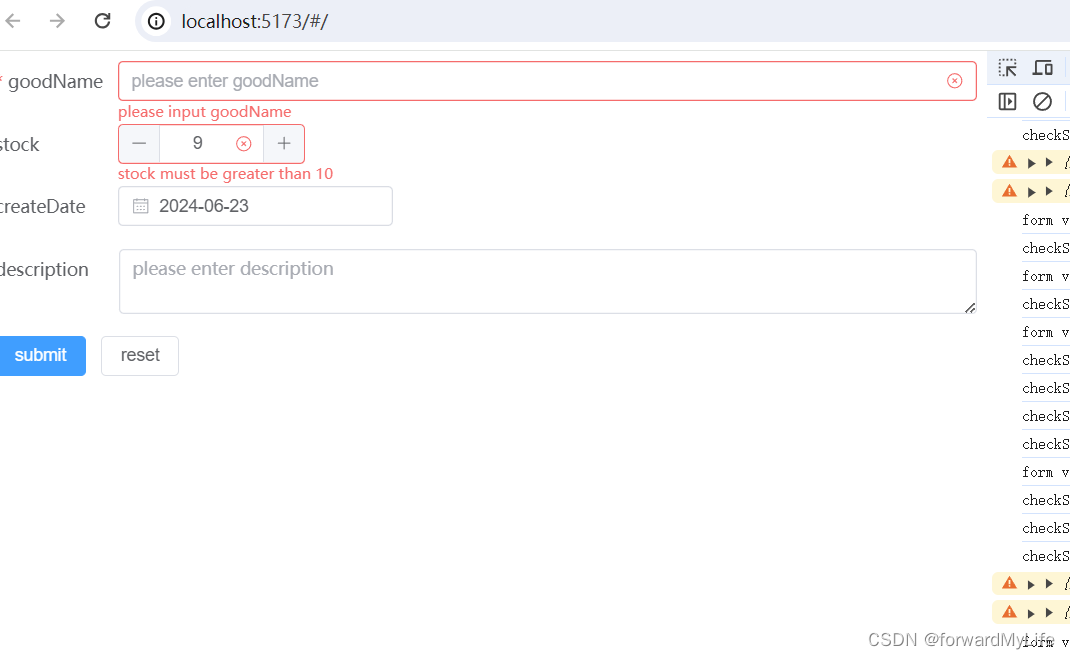
element-plus 表单组件 之element-form
elment-plus的表单组件的标签有el-form,el-form-item。 单个el-form标签内包裹若干个el-form-item,el-form-item包裹具体的表单组件,如输入框组件,多选组件,日期组件等。 el-form组件的主要作用是:提供统一的布局给其他表单组件&…...
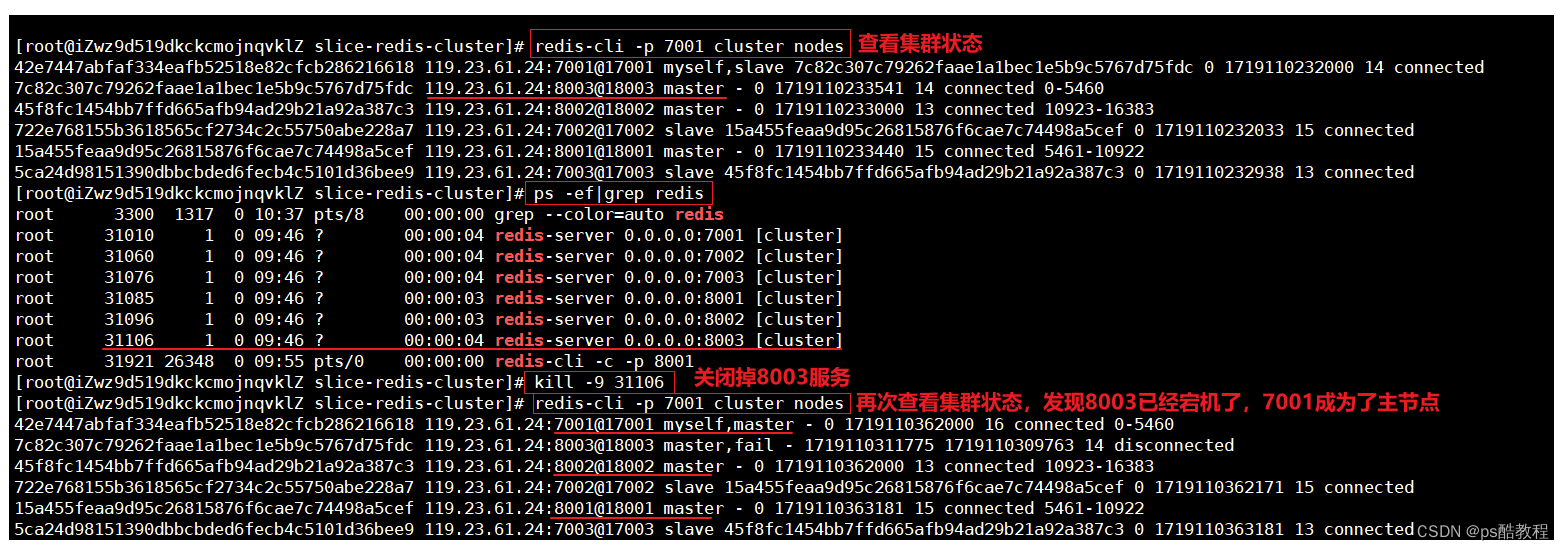
redis持久化主从哨兵分片集群
文章目录 1. 单点Redis的问题数据丢失问题并发能力问题故障恢复问题存储能力问题 2. Redis持久化 -> 数据丢失问题RDB持久化linux单机安装Redis步骤RDB持久化与恢复示例(详细)RDB机制RDB配置示例RDB的fork原理总结 AOF持久化AOF配置示例(详…...

IOS Swift 从入门到精通: 结构体的访问控制、静态属性和惰性
文章目录 初始化器引用当前实例惰性属性静态属性和方法访问控制总结初始化器 初始化器是一种特殊方法,可提供创建结构体的不同方式。所有结构体都默认带有一个初始化器,称为成员初始化器- 它会要求您在创建结构体时为每个属性提供一个值。 User如果我们创建一个具有一个属性…...

SQL题:未完成率较高的50%用户近三个月答卷情况
SQL题:未完成率较高的50%用户近三个月答卷情况 这是一道牛客网上SQL进阶图库中的一道困难题目,个人花了近两个小时才通过所有用例。之所以想记录下来是因为这道题算是一个很考验基本功的题目,也不乏一些SQL中的技巧。下面我们逐步分析&#…...

挑战与机遇的交织
AI与音乐创作:挑战与机遇的交织 引言 近年来,人工智能技术的迅猛发展使得其在各个领域都展现出了巨大的潜力和影响力,音乐创作领域也不例外。最近上线的音乐大模型,无疑是这一趋势的一个重要节点,它极大地降低了素人…...
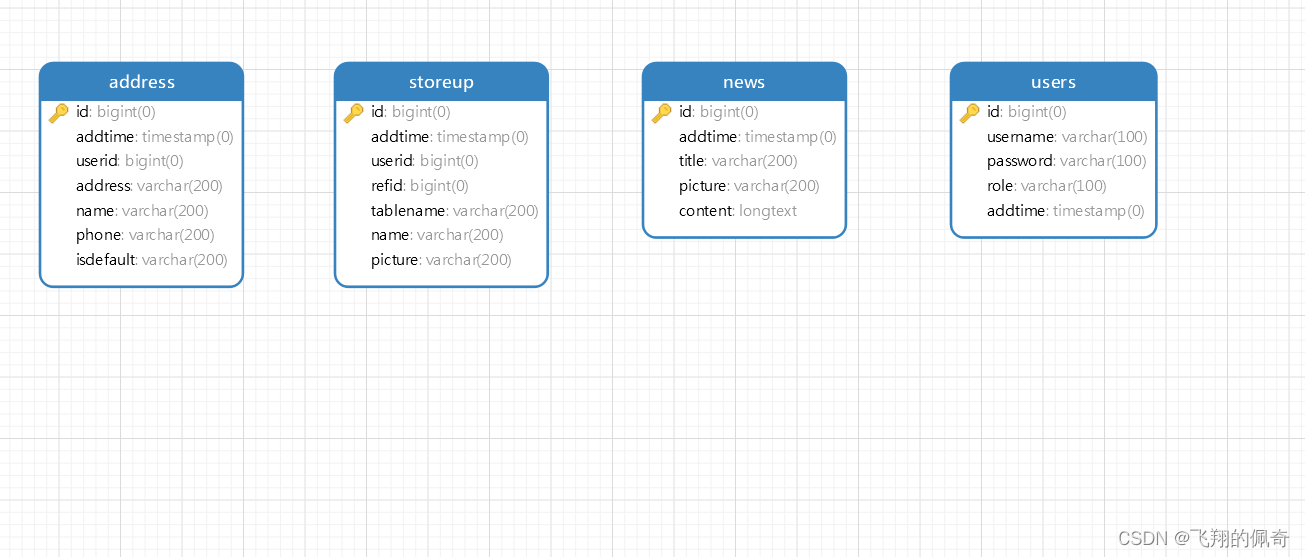
Java项目:基于SSM框架实现的精品酒销售管理系统分前后台【ssm+B/S架构+源码+数据库+毕业论文】
一、项目简介 本项目是一套基于SSM框架实现的精品酒销售管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操作简单、功…...

[论文笔记]Are Large Language Models All You Need for Task-Oriented Dialogue?
引言 今天带来论文Are Large Language Models All You Need for Task-Oriented Dialogue?的笔记。 主要评估了LLM在完成多轮对话任务以及同外部数据库进行交互的能力。在明确的信念状态跟踪方面,LLMs的表现不及专门的任务特定模型。然而,如果为它们提…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
