@PostConstruct 注解的方法用于资源的初始化
@PostConstruct 是 Java EE 5 引入的一个注解,主要用于依赖注入完成之后,需要执行的方法上。这个注解的方法会在依赖注入完成后自动被容器(如 EJB 容器或 Spring 容器)调用,并且只会被调用一次。
@PostConstruct 注解的方法必须满足以下条件:
- 该方法不能有参数
- 该方法的返回类型必须为 void
- 该方法上不能有除了 @PostConstruct 以外的其他注解
- 该方法必须是实例方法,不能是静态方法
- 该方法不能被继承(如果继承,子类的方法将不会被调用)
通常,@PostConstruct 注解的方法用于资源的初始化,例如:
import javax.annotation.PostConstruct; public class MyBean { @PostConstruct public void init() { // 初始化代码,例如数据库连接、资源加载等 System.out.println("Bean is going through init."); } // 其他方法...
}在 Spring 或其他支持该注解的容器中,当 MyBean 的实例被创建并且所有依赖注入完成后,init() 方法会被自动调用
注意:在 Spring 中,除了 @PostConstruct,你还可以使用 @InitBinder、@ModelAttribute 和 @Bean 的 initMethod 属性来执行初始化操作,但它们的用途和上下文略有不同。
相关文章:

@PostConstruct 注解的方法用于资源的初始化
PostConstruct 是 Java EE 5 引入的一个注解,主要用于依赖注入完成之后,需要执行的方法上。这个注解的方法会在依赖注入完成后自动被容器(如 EJB 容器或 Spring 容器)调用,并且只会被调用一次。 PostConstruct 注解的…...
SvelteKit教程:hello world)
(一)SvelteKit教程:hello world
(一)SvelteKit教程:hello world sveltekit 的官方教程,在这里:Creating a project • Docs • SvelteKitCreating a project • Docs • SvelteKit 我们可以按照如下的步骤来创建一个项目: npm create s…...

华为Atlas NPU ffmpeg 编译安装
处理器:鲲鹏920 NPU:昇腾 310P3 操作系统:Kylin Linux Advanced Server V10 CANN:Ascend-cann-toolkit_8.0.RC1_linux-aarch64.run FFmpeg:AscendFFmpegPlugin(不要用AscendFFmpeg) AscendFFmpegPlugin下载地址&…...
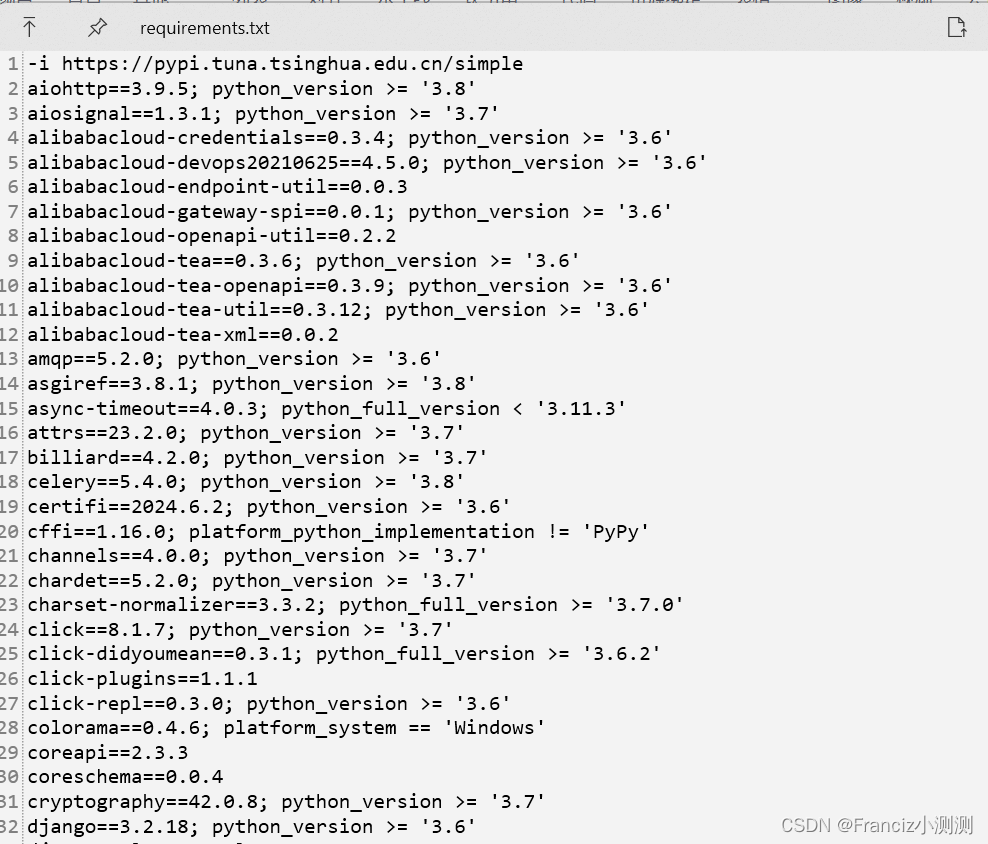
Python 虚拟环境 requirements.txt 文件生成 ;pipenv导出pip安装文件
搜索关键词: Python 虚拟环境Pipenv requirements.txt 文件生成;Pipenv 导出 pip requirements.txt安装文件 本文基于python版本 >3.9 文章内容有效日期2023年01月开始(因为此方法从这个时间开始是完全ok的) 上述为pipenv的演示版本 使用以下命令可精准生成requirement…...

Less与Sass的区别
1. 功能和工具: Sass:提供了更多的功能和内置方法,如条件语句、循环、数学函数等。Sass 也支持更复杂的操作和逻辑构建。 Less:功能也很强大,但相比之下,Sass 在功能上更为丰富和成熟。 2、编译环境&…...

力扣-2663
题目 如果一个字符串满足以下条件,则称其为 美丽字符串 : 它由英语小写字母表的前 k 个字母组成。它不包含任何长度为 2 或更长的回文子字符串。 给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。 请你找出并返回一个长度为 n 的美丽字符串&#…...

CausalMMM:基于因果结构学习的营销组合建模
1. 摘要 在线广告中,营销组合建模(Marketing Mix Modeling,MMM) 被用于预测广告商家的总商品交易量(GMV),并帮助决策者调整各种广告渠道的预算分配。传统的基于回归技术的MMM方法在复杂营销场景…...

编译 CUDA 程序的基本知识和步骤
基本工具 NVCC(NVIDIA CUDA Compiler): nvcc 是 NVIDIA 提供的 CUDA 编译器,用于将 CUDA 源代码(.cu 文件)编译成可执行文件或库。它可以处理 CUDA 和主机代码(例如 C)的混合编译。nvcc 调用底层…...
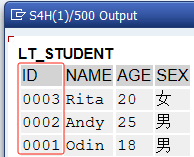
[SAP ABAP] 排序内表数据
语法格式 整表排序 SORT <itab> [ASCENDING|DESCENDING]. 按指定字段排序 SORT <itab> BY f1 [ASCENDING|DESCENDING] f2 [ASCENDING|DESCENDING] ... fn [ASCENDING|DESCENDING].<itab>:代表内表 不指定排序方式则默认升序排序 示例1 结果显…...

【UML用户指南】-21-对基本行为建模-活动图
目录 1、概念 2、组成结构 2.1、动作 2.2、活动节点 2.3、控制流 2.4、分支 2.5、分岔和汇合 2.6、泳道 2.7、对象流 2.8、扩展区域 3、一般用法 3.1、对工作流建模 3.2、对操作建模 一个活动图从本质上说是一个流程图,展现从活动到活动的控制流 活动图…...

【web2】jquary,bootstrap,vue
文章目录 1.jquary:选择器1.1 jquery框架引入:$("mydiv") 当成id选择器1.2 jquery版本/对象:$(js对象) -> jquery对象1.3 jquery的页面加载事件:$ 想象成 window.onload 1.4 jquery的基本选择器:$()里内容…...

独角兽品牌獭崎酱酒:高性价比的酱香之选
在酱香型白酒领域中,獭崎酱酒以其独特的品牌定位和高性价比迅速崛起,成为市场上备受关注的独角兽品牌。作为贵州茅台镇的一款新秀酱香酒,獭崎酱酒不仅传承了百年酿造工艺,还以创新的商业模式和亲民的价格赢得了广大消费者的青睐。…...

java打印菱形和空心菱形
java打印菱形 菱形分上下两个部分。其中上部分同打印金字塔;下部分循环部分i是递减 (ps:菱形层数只能为奇数) import java.util.Scanner;public class Lingxing{public static void main(String[] args) {Scanner myScanner new Scanner(S…...

Day10 —— 大数据技术之Scala
Scala编程入门 Scala的概述什么是Scala?Scala的重要特点Scala的使用场景 Scala的安装Scala基础Scala总结 Scala的概述 什么是Scala? Scala是一种将面向对象和函数式编程结合在一起的高级语言,旨在以简洁、优雅和类型安全的方式表达通用编程…...

Linux应用系统快速部署:docker快速部署linux应用程序
目录 一、背景 (一)引入docker的起因 (二)docker介绍 (三)Docker部署的优势 1、轻量级和可移植性 2、快速部署和扩展 3、一致性 4、版本控制 5、安全性 6、资源隔离 7、简化团队协作 8、多容器…...
?)
三目运算符中间的表达式可以省略吗(a?:c)?
熟悉C语言的童靴对三目运算符都非常熟悉,a? b : c; 如果a为true,则整个运算符的值为b,否则为c;那么问题来了,三目运算符中间的表达式可以省略吗?即a? : c; 1、linux内核中出现的省略情况 本人在阅读内核代码是发现了下面的代码: preferr…...

android 彩虹进度条自定义view实现
实现一个彩虹色进度条功能,不说明具体用途大家应该能猜到。想找别人造的轮子,但是没有合适的,所以决定自己实现一个。 相关知识 android 自定义view LinearGradient 线性渐变 实现步骤 自定义view 自定义一个TmcView类继承View 重写两…...
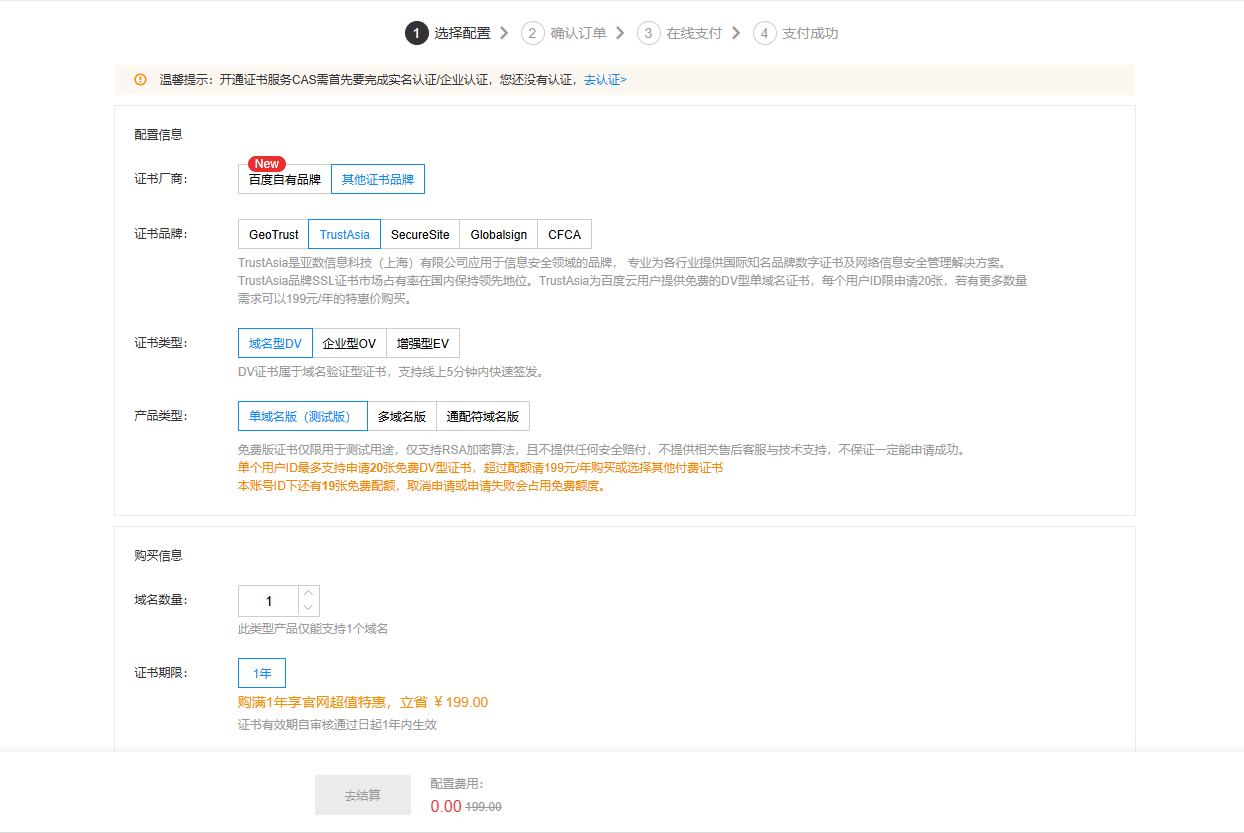
免费一年SSL证书申请——建议收藏
免费一年SSL证书申请——建议收藏 获取免费一年期SSL证书其实挺简单的 准备你的网站: 确保你的网站已经有了域名,而且这个域名已经指向你的服务器。还要检查你的服务器支持HTTPS,也就是443端口要打开,这是HTTPS默认用的。 验证域…...
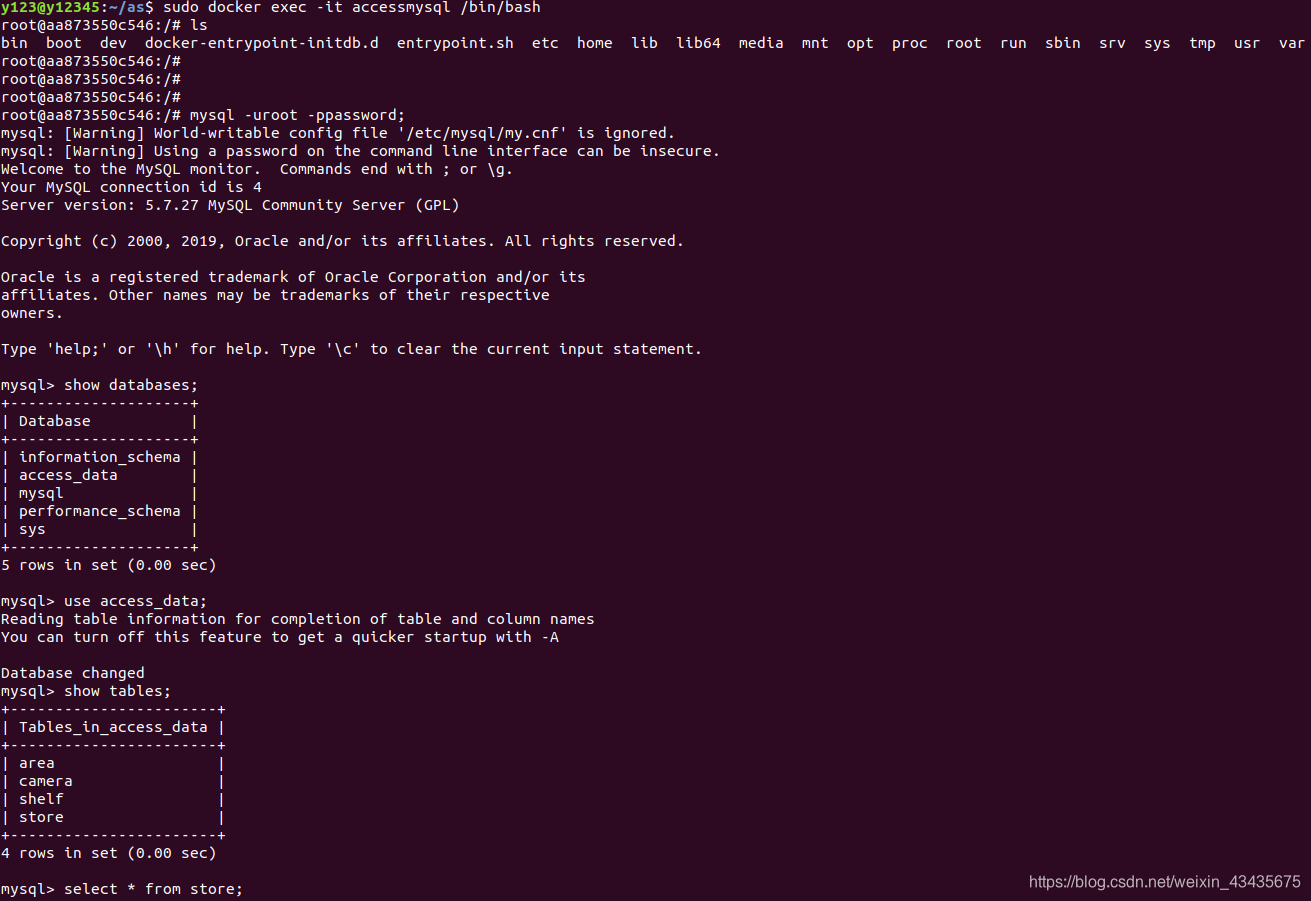
【docker1】指令,docker-compose,Dockerfile
文章目录 1.pull/image,run/ps(进程),exec/commit2.save/load:docker save 镜像id,不是容器id3.docker-compose:多容器:宿主机(eth0网卡)安装docker会生成一…...

Flutter中的异步和多进程
Flutter 是一个用于创建高性能、高保真度移动应用的框架,它使用 Dart 编程语言。 在 Flutter 中,异步和多进程是两种不同的概念,用于解决不同的问题。 异步 (Asynchronous) 异步编程是一种编程范式,允许代码在等待操作完成(如网络请求、文件 I/O)时继续执行其他任务,而不…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
