QML 中宽度、高度与隐式宽度/高度的区别及其应用场景
在 QML 中,width、height 与 implicitWidth、implicitHeight 这几个属性常常令开发者感到困惑。本文将详细介绍它们之间的区别,并说明在何种情况下应使用隐式尺寸以及普通尺寸。
基本定义
width和height:表示组件/item 的实际尺寸。implicitWidth和implicitHeight:表示组件/item 的自然尺寸,即在未明确指定尺寸时,组件自己希望占用的尺寸。
理解隐式尺寸和实际尺寸
隐式尺寸(Implicit Size)通常在创建可重用组件时使用。它表示组件在未设置明确尺寸时的自然大小。例如,一个图片的自然尺寸是其文件的实际像素大小,但这个尺寸可以被拉伸或缩小。
举例说明
假设我们有一个图片图库,其中的图片大小不一,我们希望这些图片在显示时可以缩小但不放大,此时可以使用隐式宽度和高度来存储图片的自然尺寸:
Image {width: Math.max(150, implicitWidth)height: Math.max(150, implicitHeight)
}
对于自定义组件,可以选择将尺寸定义为相对于组件的根节点,例如:
Item {id: rootRectangle {width: root.width * 0.2height: root.height * 0.2color: 'red'}Rectangle {x: 0.2 * root.widthy: 0.2 * root.heightwidth: root.width * 0.8height: root.height * 0.8color: 'green'}
}
在这种情况下,组件没有自然尺寸,任何设置的尺寸都能完美地适配。
相反,如果我们有一个具有自然尺寸的对象,例如某些固定尺寸的组件:
Item {id: rootproperty alias model: repeater.modelRepeater {id: repeaterdelegate: Rectangle {width: 100height: 100x: 102 * indexy: 102 * index}}
}
在这种情况下,应向用户提供关于自然尺寸的信息,用户可以决定是否设置一个更小的尺寸并处理溢出,例如通过裁剪内容。
隐式尺寸的实际应用
在许多情况下,childrenRect.height 和 childrenRect.width 是隐式尺寸的良好度量标准,但也有例外。例如,当内容的 x 坐标为负值时,使用 childrenRect 可能并不合适。
一个实际例子是 Flickable,它专门用于包含比自身尺寸更大的对象。使 Flickable 的尺寸等于其内容的尺寸是不自然的。
注意,在自定义组件中使用 scale 时要小心,因为 childrenRect 不会意识到缩放。
Item {id: rootimplicitWidth: child.width * child.scaleimplicitHeight: child.height * child.scaleRectangle {id: childwidth: 100height: 100scale: 3color: 'red'}
}
实践准则
- 当需要设置可重用组件的根节点的尺寸时,使用
implicitWidth和implicitHeight。 - 在某些情况下,如果节点作为属性暴露出来,也可以为非根节点设置隐式尺寸。
- 使用组件时,设置
width和height。
隐式尺寸不是必需的,但它们的存在是为了方便,并成为一种约定。
结论
理解和正确使用 width、height 与 implicitWidth、implicitHeight 对于 QML 开发者来说非常重要。隐式尺寸主要在描述组件的自然尺寸时使用,而实际尺寸在组件的布局和显示中更为常见。通过正确使用这些属性,可以创建更灵活和可重用的组件。
相关文章:

QML 中宽度、高度与隐式宽度/高度的区别及其应用场景
在 QML 中,width、height 与 implicitWidth、implicitHeight 这几个属性常常令开发者感到困惑。本文将详细介绍它们之间的区别,并说明在何种情况下应使用隐式尺寸以及普通尺寸。 基本定义 width 和 height:表示组件/item 的实际尺寸。impli…...
解决事务管理中的方法调用问题)
如何利用AopContext.currentProxy()解决事务管理中的方法调用问题
在Spring应用开发中,使用AOP(面向切面编程)来管理事务是非常常见的做法。然而,在某些场景下,尤其是在同一个类的方法内部,一个非事务方法直接调用另一个带有事务注解的方法时,可能会遇到事务不生…...
VMware虚拟机下载安装Windows Server 2016
「作者简介」:2022年北京冬奥会网络安全中国代表队,CSDN Top100,就职奇安信多年,以实战工作为基础对安全知识体系进行总结与归纳,著作适用于快速入门的 《网络安全自学教程》,内容涵盖系统安全、信息收集等…...
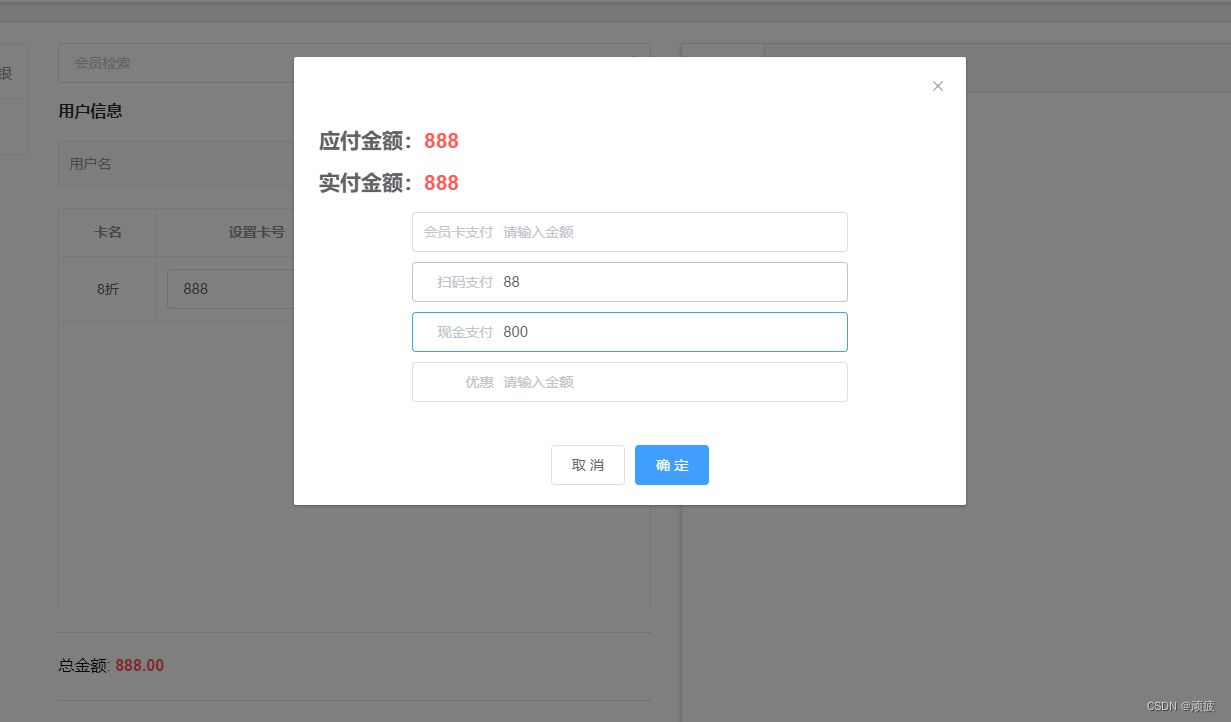
springboot vue 开源 会员收银系统 (7) 收银台的完善 新增开卡 结算
前言 完整版演示 开发版演示 在前面的开发中,我们成功完成了商品分类和商品信息的搭建,开发了收银台基础。现在,我们将进一步完善收银台的功能,添加开卡和结算功能,并在后台实现会员卡的创建和订单保存。同时ÿ…...
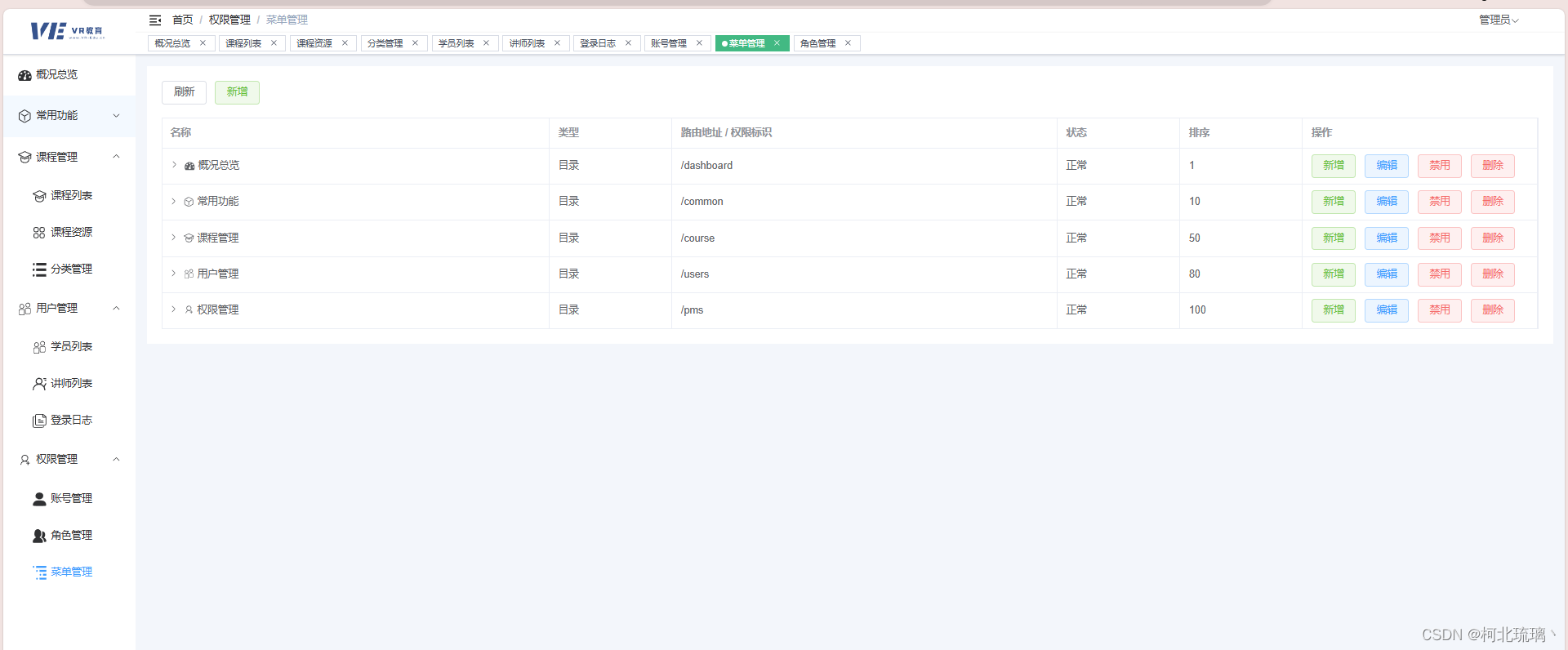
虚拟现实环境下的远程教育和智能评估系统(十三)
管理/教师端前端工作汇总education-admin: 首先是登录注册页面的展示 管理员 首页 管理员登录后的首页如下图所示 管理员拥有所有的权限 课程管理 1、可以查看、修改、增添、删除课程列表内容 2、可以对课程资源进行操作 3、可以对课程的类别信息进行管理&…...

深入了解软件设计模式:创新应用与优化代码结构
前言 在软件开发中,设计模式被广泛应用,通常分为三大类:创建型、结构型和行为型。这些模式经过时间验证,在解决特定问题和优化代码结构方面发挥了重要作用。本文将详细介绍每一类设计模式,并通过具体实例展示它们的应…...
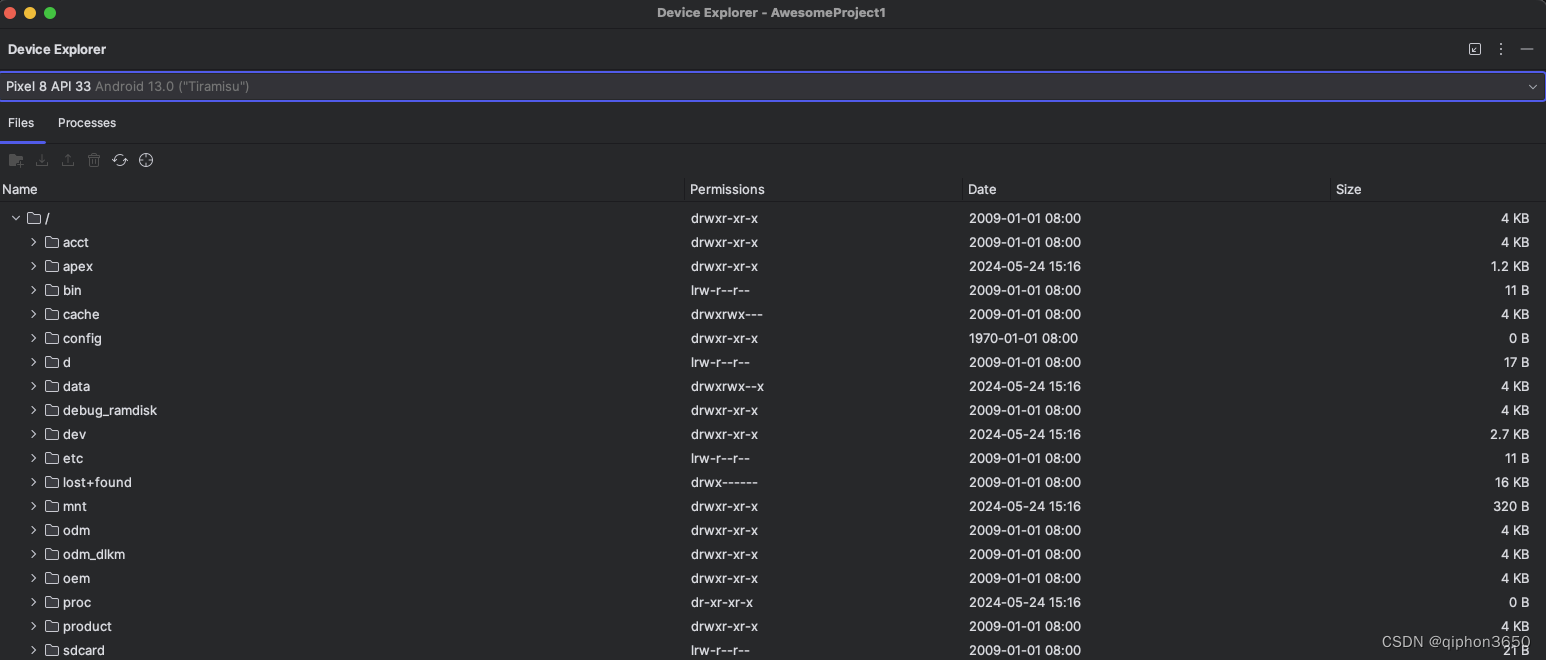
android studio 模拟器文件查找
android studio 模拟器文件查找 使用安卓模拟器下载文件后通常无法在系统硬盘上找到下载的文件,安卓 studio studio 其实提供了文件浏览工具,找到后可以直接使用 Android studio 打开 打开 Android studioview 菜单view > Tool Windows > Device…...
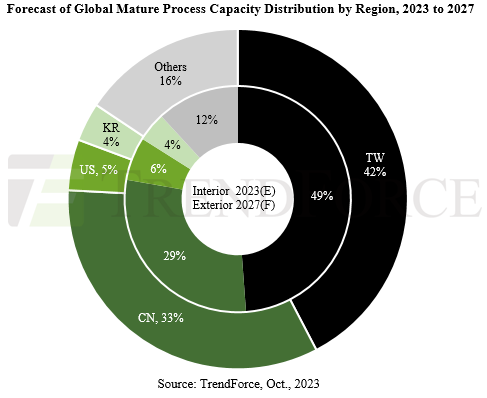
【科普】半导体制造过程的步骤、技术、流程
在这篇文章中,我们将学习基本的半导体制造过程。为了将晶圆转化为半导体芯片,它需要经历一系列复杂的制造过程,包括氧化、光刻、刻蚀、沉积、离子注入、金属布线、电气检测和封装等。 基本的半导体制造过程 1.晶圆(Wafer…...

c89、c99、c11
C99 标准开始引入了 // 单行注释。在此之前,C语言只支持 /* ... */ 多行注释。 具体说明: // 单行注释:在C99标准(ISO/IEC 9899:1999)引入之前,C语言中没有单行注释。C99标准借鉴了C的注释风格࿰…...
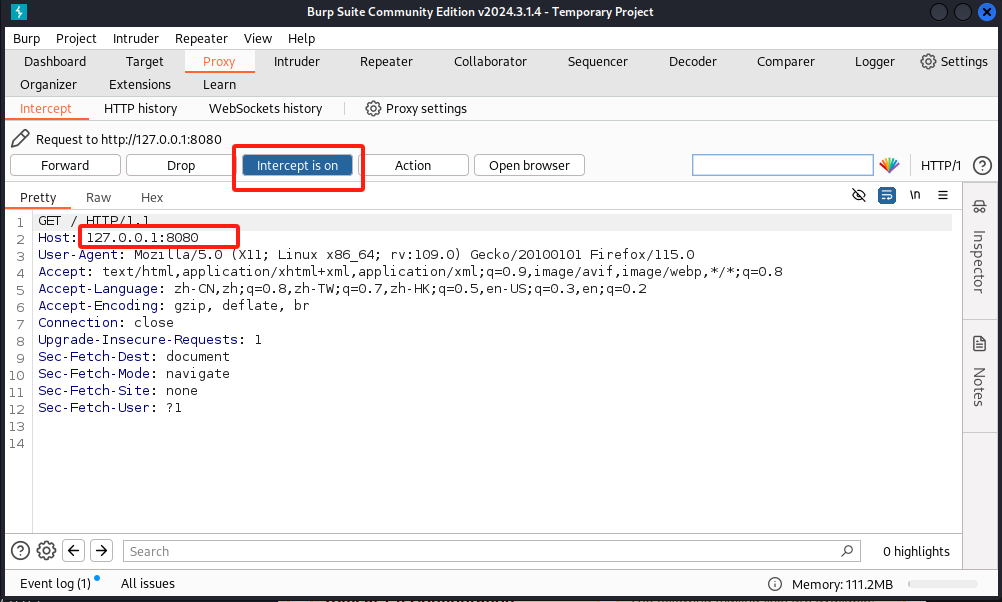
【网络安全的神秘世界】已解决burpsuite报错Failed to start proxy service on 127.0.0.1:8080
🌝博客主页:泥菩萨 💖专栏:Linux探索之旅 | 网络安全的神秘世界 | 专接本 | 每天学会一个渗透测试工具 解决burpsuite无法在 127.0.0.1:8080 上启动代理服务端口被占用以及抓不到本地包的问题 Burpsuite无法启动proxy…...

【C#】使用数字和时间方法ToString()格式化输出字符串显示
在C#编程项目开发中,几乎所有对象都有格式化字符串方法,其中常见的是数字和时间的格式化输出多少不一样,按实际需要而定吧,现记录如下,以后会用得上。 文章目录 数字格式化时间格式化 数字格式化 例如,保留…...

Mac系统主机名变为bogon的解决方案
如题 在使用Mac操作系统时,您可能会遇到一个有趣且略显困扰的问题:终端中显示的主机名突然变成了“bogon”。这不仅让人困惑,还可能给日常操作带来不便。本文旨在提供一种简便的解决方法,帮助您将主机名恢复为正常状态。 什么是…...

行列式和矩阵的区别
目录 一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数 二、矩阵 1. 矩阵的定义 三、行列式和矩阵的区别 四、参考书目 一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数 二、矩阵 1. 矩阵的定义 三、行列式和矩阵的区别 四、参考书目 同济大学数学系. 工程数学…...

MATLAB复习
MATLAB常用的标点符号 空格 变量分隔符 矩阵一行中各元素间的分隔符 程序语句关键词分隔符 逗号,分隔显示计算结果的各语句 变量分隔符 矩阵中一行各元素的分隔符点号.数值中的小数点 结构数组的域访问符分号;分隔不想显示计算结果的各语句 矩阵行与行的…...

Android11 动态权限申请
1、单个权限检查及申请 private void checkSinglePermission(){// 在需要的地方,如Activity中if (ContextCompat.checkSelfPermission(this, Manifest.permission.READ_PHONE_STATE)! PackageManager.PERMISSION_GRANTED) {ActivityCompat.requestPermissions(this,…...

线性卷积(相关)和圆周卷积(相关)以及FFT之间的关系(AEC举例)
时域自适应滤波算法中的线性卷积和线性相关运算量较大,导致计算复杂度升高,我们更愿意把这两个信号变换到频域,通过频域相乘的方式来取代时域复杂度相当高的卷积或相关运算。 预备知识:线性卷积(相关)和圆…...
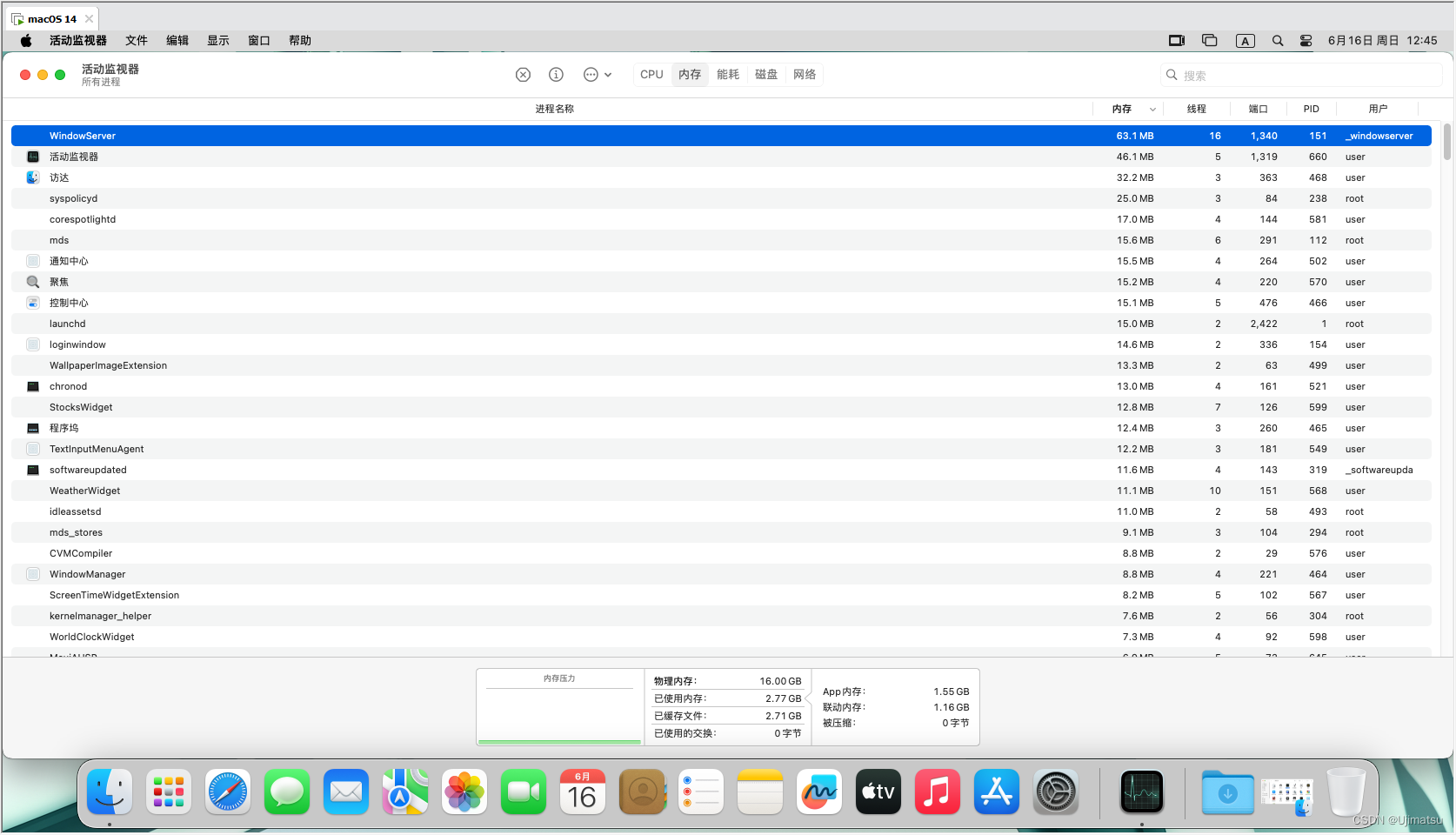
AMD平台,5600X+6650XT,虚拟机安装macOS 14(2024年6月)
AMD平台安装macOS 14的麻烦,要比Intel平台多的多,由于macOS从13开始,对CPU寄存器的读取进行了改变,导致AMD平台只要安装完macOS 13及以后版本,开机后就报五国语言错误,不断重启。改vmx文件,被证…...
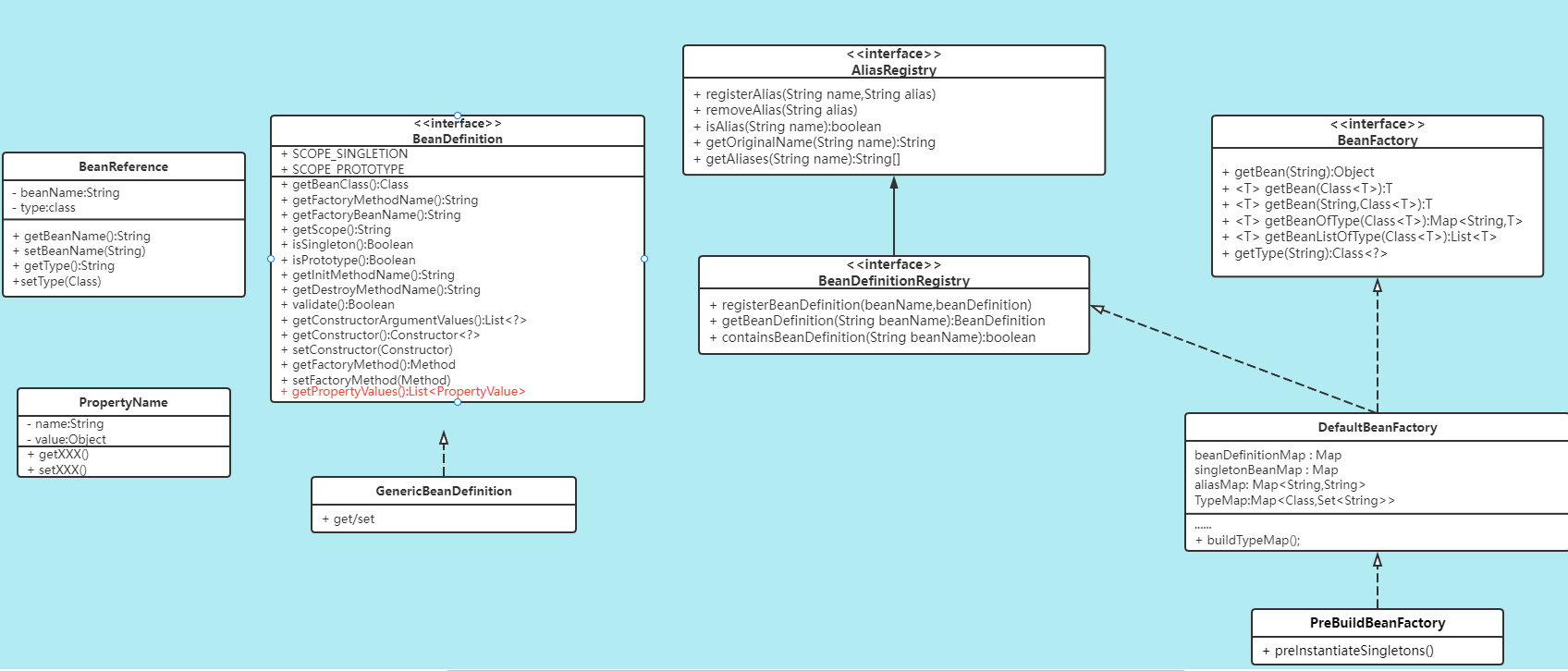
Spring源码之手写DI
Spring源码之手写DI 我们来回顾一下前面手写IOC的内容。 一、DI介绍 DI(Dependency injection)依赖注入。对象之间的依赖由容器在运行期决定,即容器动态的将某个依赖注入到对象之中。说直白点就是给Bean对象的成员变量赋值。 在这里我们就需要明白几个问题。 1.…...
从零入手人工智能(5)—— 决策树
1.前言 在上一篇文章《从零入手人工智能(4)—— 逻辑回归》中讲述了逻辑回归这个分类算法,今天我们的主角是决策树。决策树和逻辑回归这两种算法都属于分类算法,以下是决策树和逻辑回归的相同点: 分类任务࿱…...
)
go语言:两协程并发交替打印数字和字母(代码逐行注释)
要求: 并发两协程交替打印数字和字母。一个协程打印数字,一个协程打印字母。 输出: 12AB34CD56EF78GH910IJ1112KL1314MN1516OP1718QR1920ST2122UV2324WX2526YZ2728 思路: 两个 channel 控制两个协程进行交替打印。sync.WaitG…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
