数据结构9——排序
一、冒泡排序
冒泡排序(Bubble Sort),顾名思义,就是指越小的元素会经由交换慢慢“浮”到数列的顶端。
算法原理
- 从左到右,依次比较相邻的元素大小,更大的元素交换到右边;
- 从第一组相邻元素比较到最后一组相邻元素,这一步结束最后一个元素必然是参与比较的元素中最大的元素;
- 按照大的居右原则,重新从左到后比较,前一轮中得到的最后一个元素不参4与比较,得出新一轮的最大元素;
- 按照上述规则,每一轮结束会减少一个元素参与比较,直到没有任何一组元素需要比较。
代码实现
// 冒泡排序
void BubbleSort(int* arr, int n)
{int i = 0;for (i = 0; i < n - 1; ++i) // 冒泡排序趟数{int j = 0;int flag = 1;for (j = 0; j < n - i - 1; ++j) // 待排序区间进行比较交换{if (arr[j] > arr[j + 1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;flag = 0;}}if (flag == 1){// 说明已经有序break;}}
}
拓展:

O()
二、快速排序
快速排序(Quick Sort),是冒泡排序的改进版,之所以“快速”,是因为使用了分治法。它也属于交换排序,通过元素之间的位置交换来达到排序的目的。
算法原理
在序列中随机挑选一个元素作基准,将小于基准的元素放在基准之前,大于基准的元素放在基准之后,再分别对小数区与大数区进行排序。
一趟快速排序的具体做法是:
- 设两个指针 i 和 j,分别指向序列的头部和尾部;
- 先从 j 所指的位置向前搜索,找到第一个比基准小的值,把它与基准交换位置;
- 再从 i 所指的位置向后搜索,找到第一个比基准大的值,把它与基准交换位置;
- 重复 2、3 两步,直到 i = j。
仔细研究一下上述算法我们会发现,在排序过程中,对基准的移动其实是多余的,因为只有一趟排序结束时,也就是 i = j 的位置才是基准的最终位置。
由此可以优化一下算法:
- 设两个指针 i 和 j,分别指向序列的头部和尾部;
- 先从 j 所指的位置向前搜索,找到第一个比基准小的数值后停下来,再从 i 所指的位置向后搜索,找到第一个比基准大的数值后停下来,把 i 和 j 指向的两个值交换位置;
- 重复步骤 2,直到 i = j,最后将相遇点指向的值与基准交换位置。

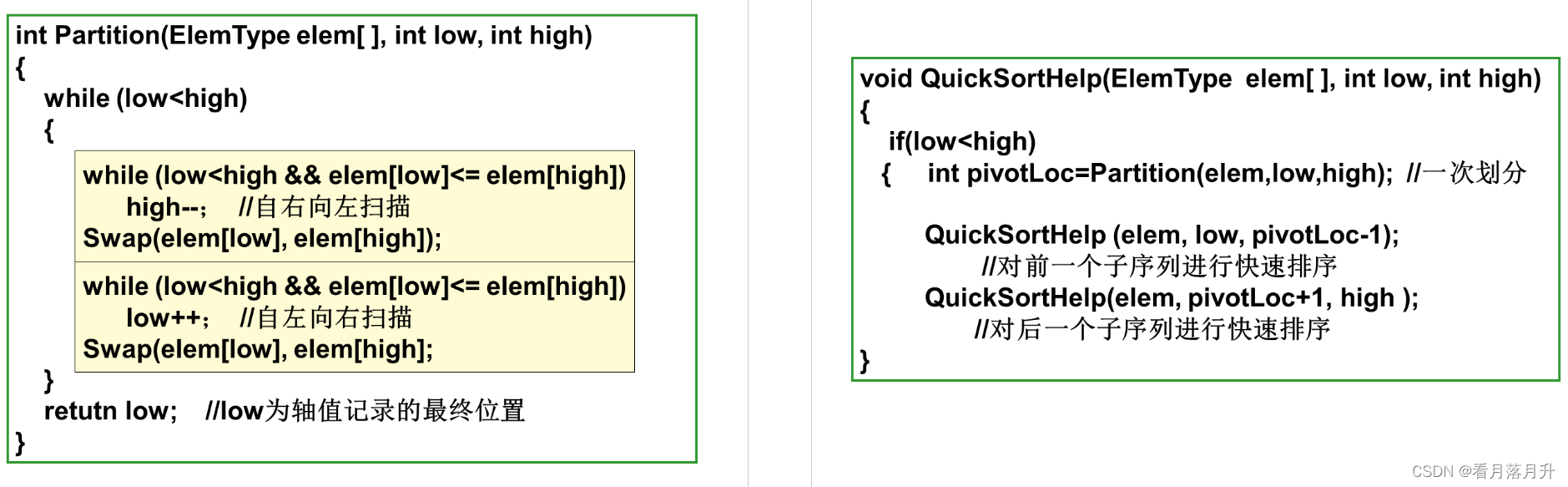
代码:
void QuickSort(int array[], int low, int high) {int i = low; int j = high;if(i >= j) {return;}int temp = array[low];while(i != j) {while(array[j] >= temp && i < j) {j--;}while(array[i] <= temp && i < j) {i++;}if(i < j) {swap(array[i], array[j]);}}//将基准temp放于自己的位置,(第i个位置)swap(array[low], array[i]);QuickSort(array, low, i - 1);QuickSort(array, i + 1, high);
}三、插入排序
直接插入排序(Straight Insertion Sort),是一种简单直观的排序算法,它的基本操作是不断地将尚未排好序的数插入到已经排好序的部分,好比打扑克牌时一张张抓牌的动作。在冒泡排序中,经过每一轮的排序处理后,序列后端的数是排好序的;而对于插入排序来说,经过每一轮的排序处理后,序列前端的数都是排好序的。
算法原理
先将第一个元素视为一个有序子序列,然后从第二个元素起逐个进行插入,直至整个序列变成元素非递减有序序列为止。如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入大相等元素的后面。整个排序过程进行 n-1 趟插入
代码:
//========================写法1=======================
void insert_sort(int *arr, int len){int i, j;for (i = 1; i < len; i++){int tmp = arr[i];//待插入数for (j = i; j > 0 && arr[j - 1] > tmp; j--){arr[j] = arr[j - 1];//大的数依次右移}arr[j] = tmp;}
}//==========================写法2======================
void insert_sort_1(int *arr, int n)
{int i = 0, j = 0;for (i = 1; i < n; i++){j = i;//一直拿当前数与前面数比,有<=它的就停止,没有接着交换位置并往前比while (j >= 1){if (arr[j] < arr[j - 1]) {swap(arr, j, j - 1);}j--;}}
}
四、希尔排序
希尔排序(Shell’s Sort)是第一个突破 O(n²) 的排序算法,是直接插入排序的改进版,又称“缩小增量排序”(Diminishing Increment Sort)。它与直接插入排序不同之处在于,它会优先比较距离较远的元素。
算法原理
先将整个待排序列分割成若干个子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
子序列的构成不是简单地“逐段分割”,将相隔某个增量的记录组成一个子序列,让增量逐趟缩短,直到增量为 1 为止。
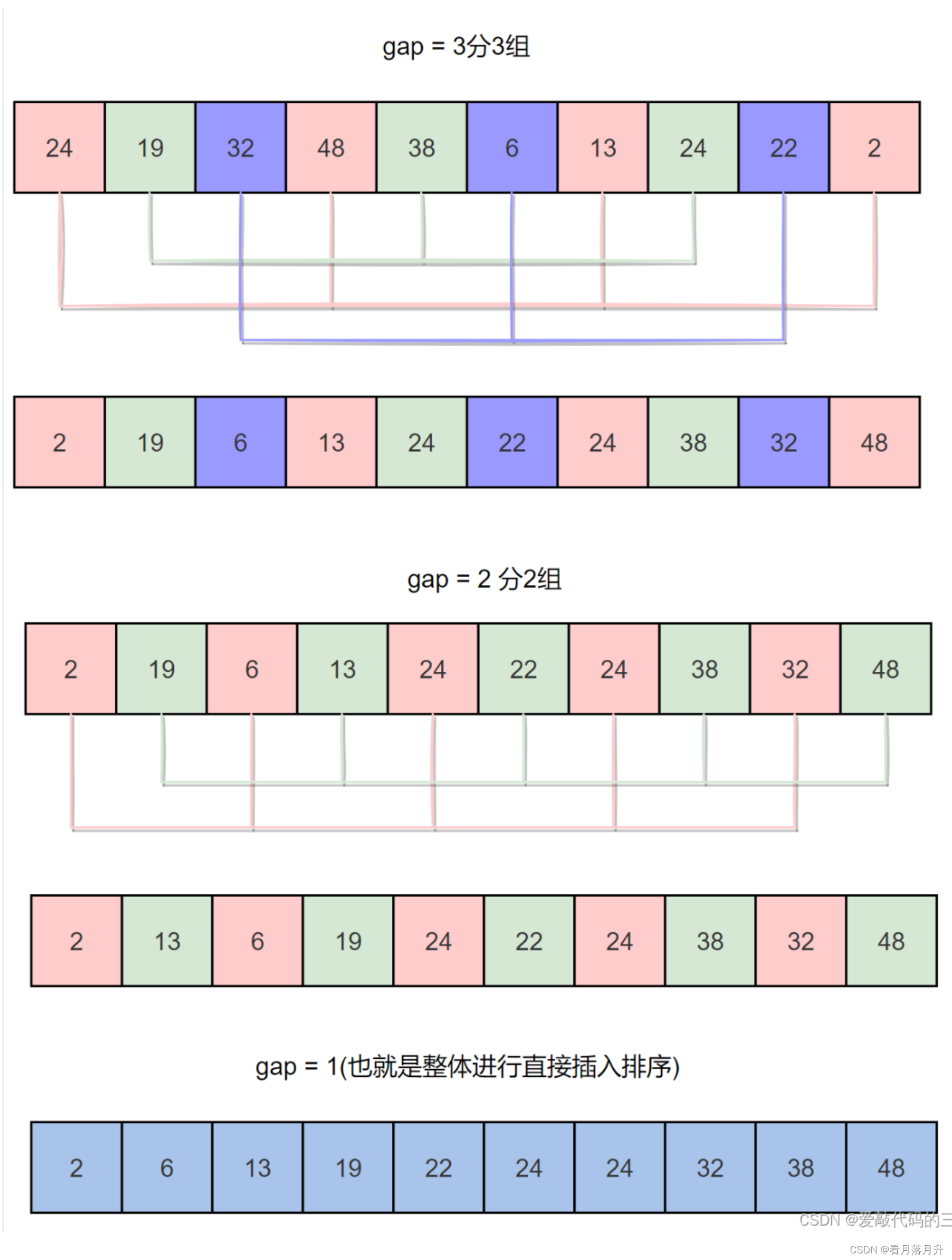

代码实现
这里的代码是通过一次就把所有元素排序完成。
- gap的取值保证最后为1就可以了
- gap不等于1之前其实都是预排序,让数据趋近于有序。
// 希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//保证最后gap为1就可以了int i = 0;for (i = 0; i < n - gap; ++i)//多组元素同时进行插入排序{int end = i;int tmp = arr[end+gap];while (end >= 0){if (arr[end] > tmp){arr[end+gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}五、选择排序
每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的元素排序完。
原理
每次从无序区间中选取一个最大(或最小)的一个元素,存放在无序区间的最后(或最前),直到全部待排序的元素排序完。
在元素集合中a r r [ i ] a r r [ n − 1 ] arr[i]~arr[n-1]arr[i] arr[n−1]中选择最大(最小的元素)
若它不是这组元素中的最后一个(第一个元素),则将它与这组元素中的最后一个(第一个)元素交换
在剩余的a r r [ i ] a r r [ n − 2 ] arr[i]~arr[n-2]arr[i] arr[n−2]集合中,重复此步骤,直到集合中剩余一个元素为止
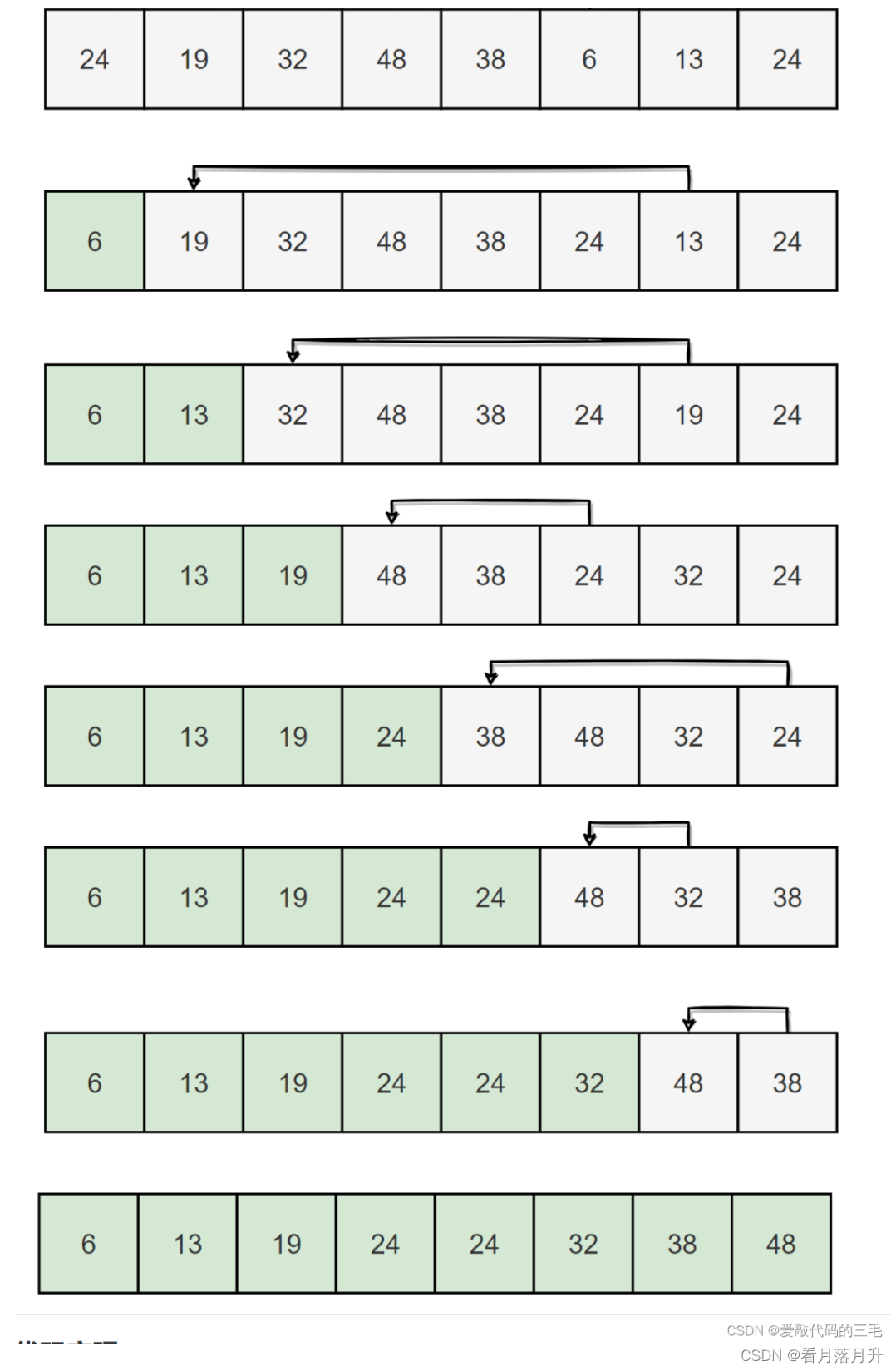
代码:
// 选择排序
void SelectSort(int* arr, int n)
{int i = 0;for (i = 0; i < n - 1; ++i){int minIndex = i;//记录待排序区间最小元素下标int j = 0;for (j = i + 1; j < n; ++j){if (arr[minIndex] > arr[j]){minIndex = j;}}int tmp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = tmp;}
}六、堆排序
堆排序是利用数据结构堆的特性来进行排序,它也是一种选择排序,它通过堆来选取数据。排升序建大堆,排降序建小堆。
堆的详细介绍可以看这一篇文章数据结构堆的详解
原理
每次将堆顶元素和最后一个元素进行交换,再进行向下调整,然后缩小待排序区间,直到数据有序,因为堆顶的元素一定是一组数据中的最大或者最小值。
注意:向下调整的前提是,这个根节点的左右子树一定要是一个堆(大堆或小堆)
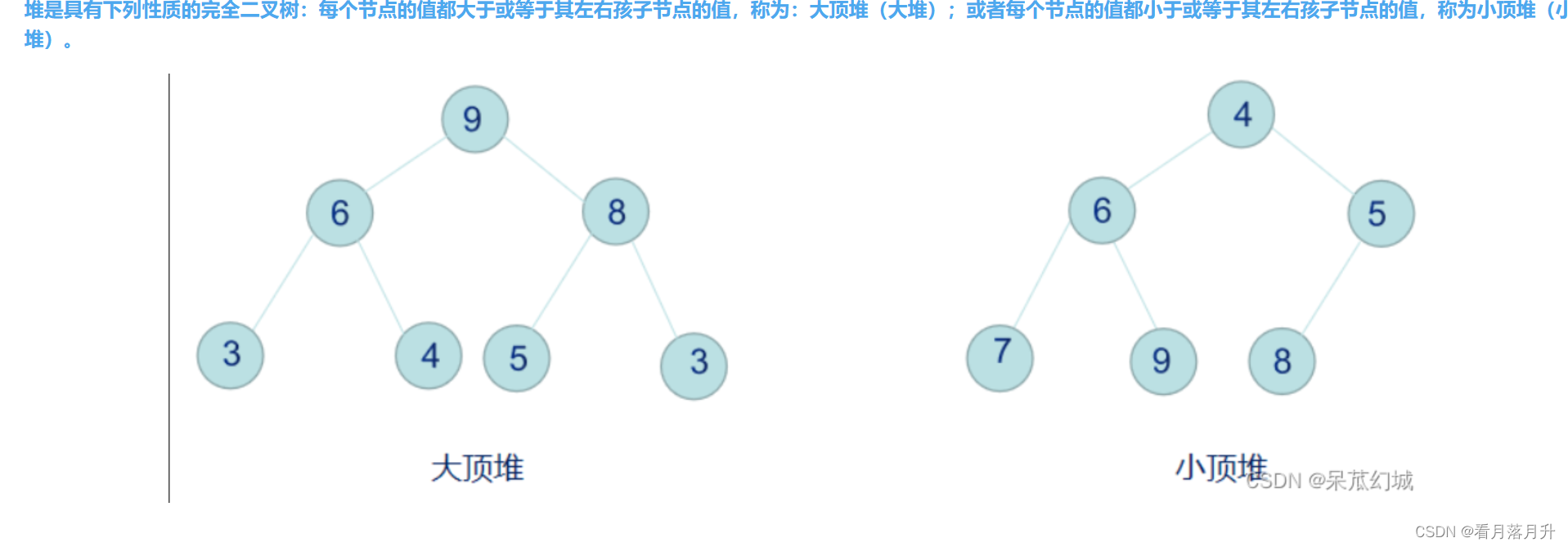

代码
void HeapAdjust(int* arr, int start, int end)
{int tmp = arr[start];for (int i = 2 * start + 1; i <= end; i = i * 2 + 1){if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子{i++;}//i一定是左右孩子的最大值if (arr[i] > tmp){arr[start] = arr[i];start = i;}else{break;}}arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{//第一次建立大根堆,从后往前依次调整for(int i=(len-1-1)/2;i>=0;i--){HeapAdjust(arr, i, len - 1);}//每次将根和待排序的最后一次交换,然后在调整int tmp;for (int i = 0; i < len - 1; i++){tmp = arr[0];arr[0] = arr[len - 1-i];arr[len - 1 - i] = tmp;HeapAdjust(arr, 0, len - 1-i- 1);}
}
int main()
{int arr[] = { 9,5,6,3,5,3,1,0,96,66 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));printf("排序后为:");for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}相关文章:

数据结构9——排序
一、冒泡排序 冒泡排序(Bubble Sort),顾名思义,就是指越小的元素会经由交换慢慢“浮”到数列的顶端。 算法原理 从左到右,依次比较相邻的元素大小,更大的元素交换到右边;从第一组相邻元素比较…...

分布式锁实现方案-基于Redis实现的分布式锁
目录 一、基于Lua看门狗实现 1.1 缓存实体 1.2 延迟队列存储实体 1.3 分布式锁RedisDistributedLockWithDog 1.4 看门狗线程续期 1.5 测试类 1.6 测试结果 1.7 总结 二、RedLock分布式锁 2.1 Redlock分布式锁简介 2.2 RedLock测试例子 2.3 RedLock 加锁核心源码分析…...

MTK7628+MT7612 加PA定频数据
1、硬件型号TR726A5G121-DPA PC9.02.0017。如下所示: 2、WIFI5.8 AC模式 42(5120MHz)信道,80带宽 3、WIFI5.8 AC模式 38(5190MHz)信道,40带宽 4、WIFI5.8 AC模式 36(5180 MHz&…...

[信号与系统]关于双线性变换
前言 本文还是前置知识 双线性变换法 双线性变换法(Bilinear Transform)是一种用于将模拟滤波器转换为数字滤波器的方法。它通过将模拟域中的s平面上的传递函数映射到数字域中的z平面上的传递函数来实现这一转换。双线性变换法保证了频率响应在转换过…...
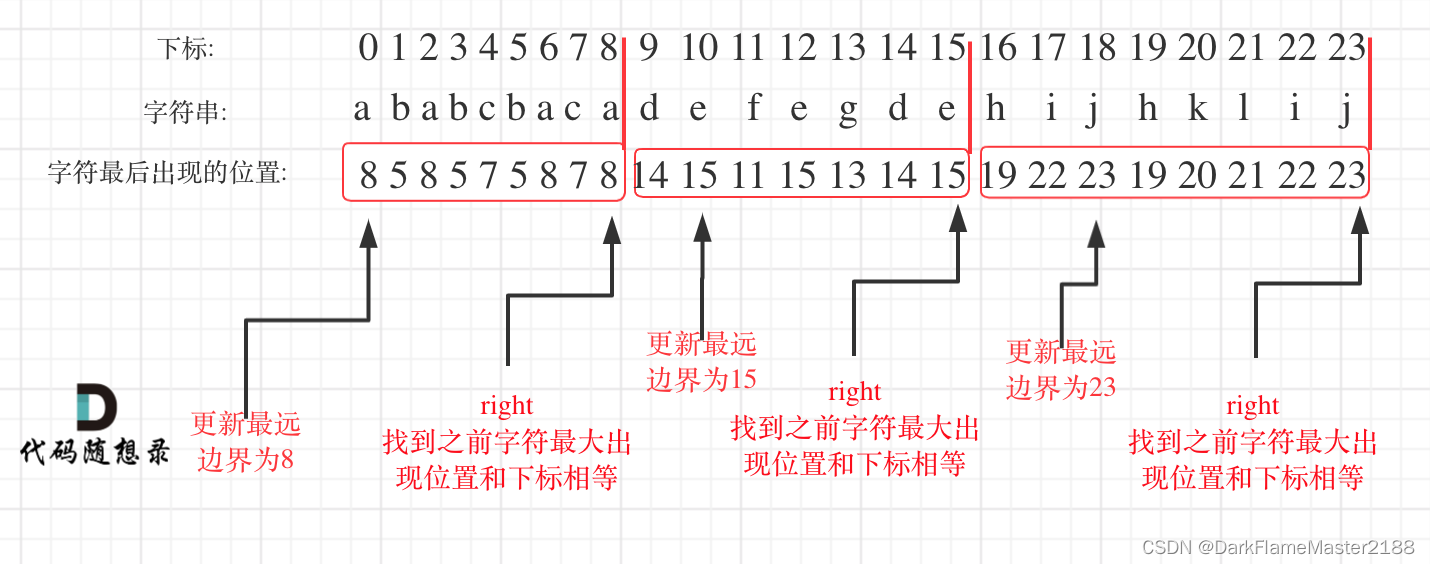
763. 划分字母区间
题目:给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。返回一个表示每个字符串片段的长度的列表…...

【PostgreSQL】AUTO_EXPLAIN - 慢速查询的日志执行计划
本文为云贝教育 刘峰 原创,请尊重知识产权,转发请注明出处,不接受任何抄袭、演绎和未经注明出处的转载。 一、介绍 在本文中,我们将了解 PostgreSQL AUTO_EXPLAIN功能的工作原理,以及为什么应该使用它来收集在生产系统…...

讯飞星火超自然语言合成的完整Demo
依赖文件和功能 requirements.txt 该文件列出了所需的依赖包。 data.py 定义了应用的配置信息,如APPId,APIKey,APISecret等。包含请求数据和请求URL。 main.py 主程序,设置了WebSocket连接,定义了处理消息的各个回调函…...
)
封装一个上拉加载的组件(无限滚动)
一、封装 1.这个是在vue3环境下的封装 2.整体思路: 2.1传入一个elRef,其实就是一个使用页面的ref。 2.2也可以不传elRef,则默认滚动的是window。 import { onMounted, onUnmounted, ref } from vue; import { throttle } from underscore;ex…...
)
WHAT - 高性能和内存安全的 Rust(二)
目录 1. 所有权(Ownership)2. 借用(Borrowing)不可变借用可变借用 3. 可变性(Mutability)4. 作用域(Scope)综合示例 了解 Rust 的所有权(ownership)、借用&am…...

办理河南建筑工程乙级设计资质的流程与要点
办理河南建筑工程乙级设计资质的流程与要点 办理河南建筑工程乙级设计资质的流程与要点主要包括以下几个方面: 流程: 工商注册与资质规划:确保企业具有独立法人资格,完成工商注册,并明确乙级设计资质的具体要求&…...

分类算法和回归算法区别
分类算法和回归算法在机器学习中扮演着不同的角色,它们的主要区别体现在输出类型、应用场景以及算法目标上。以下是对两者区别和使用场景的详细分析: 一、区别 1.输出类型: 分类算法:输出是离散的类别标签,通常表示为…...
利用Frp实现内网穿透(docker实现)
文章目录 1、WSL子系统配置2、腾讯云服务器安装frps2.1、创建配置文件2.2 、创建frps容器 3、WSL2子系统Centos服务器安装frpc服务3.1、安装docker3.2、创建配置文件3.3 、创建frpc容器 4、WSL2子系统Centos服务器安装nginx服务 环境配置:一台公网服务器(…...

怎么用Excel生成标签打印模板,自动生成二维码
环境: EXCEL2021 16.0 问题描述: 怎么用excel生成标签打印模板自动生成二维码 解决方案: 在Excel中生成标签打印模板并自动生成二维码,可以通过以下几个步骤完成: 1. 准备数据 首先,确保你的Excel表…...
java基于ssm+jsp 美食推荐管理系统
1前台首页功能模块 美食推荐管理系统,在系统首页可以查看首页、热门美食、美食教程、美食店铺、美食社区、美食资讯、我的、跳转到后台等内容,如图1所示。 图1前台首页功能界面图 用户注册,在注册页面可以填写用户名、密码、姓名、联系电话等…...
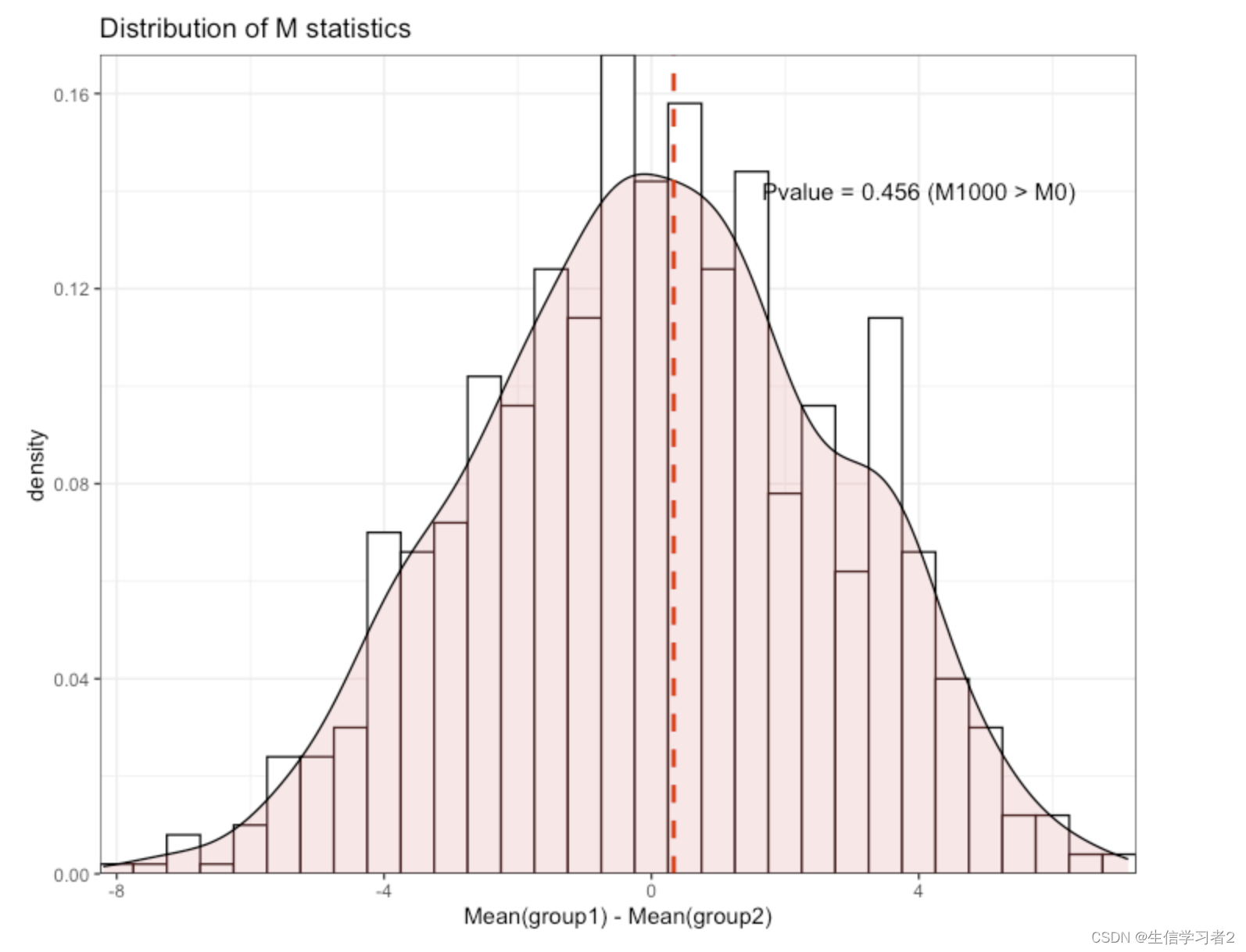
数据分析:置换检验Permutation Test
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 置换检验是一种非参数统计方法,它不依赖于数据的分布形态,因此特别适…...
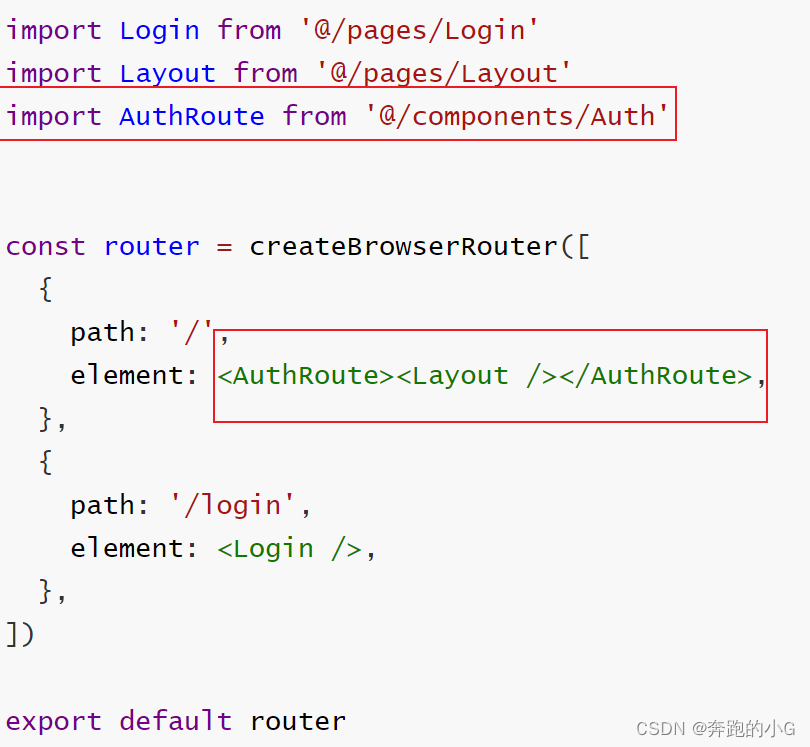
【React】使用Token做路由权限控制
在components/AuthRoute/index.js中 import { getToken } from /utils import { Navigate } from react-router-domconst AuthRoute ({ children }) > {const isToken getToken()if (isToken) {return <>{children}</>} else {return <Navigate to"/…...

机器学习周记(第四十四周:Robformer)2024.6.17~2024.6.23
目录 摘要ABSTRACT1 论文信息1.1 论文标题1.2 论文摘要1.3 论文引言1.4 论文贡献 2 论文模型2.1 问题描述2.2 Robformer2.2.1 Encoder2.2.2 Decoder 2.3 鲁棒序列分解模块2.4 季节性成分调整模块 摘要 本周阅读了一篇利用改进 Transformer 进行长时间序列预测的论文。论文模型…...

JAVA学习笔记DAY10——SpringBoot基础
文章目录 SpringBoot3 介绍SpringBoot 快速入门SpringBootApplication SpringBoot 配置文件统一配置管理Yaml 配置优势tips SpringBoot 整合 SpringMVC静态资源拦截器 interceptor SpringBoot 整合 DruidSpringBoot 整合 MybatisSpringBoot 整合 tx aopSpringBoot 打包 SpringB…...

如何在Android中实现多线程与线程池?
目录 一、Android介绍二、什么是多线程三、什么是线程池四、如何在Android中实现多线程与线程池 一、Android介绍 Android是一种基于Linux内核的开源操作系统,由Google公司领导开发。它最初于2007年发布,旨在为移动设备提供一种统一、可扩展的操作系统。…...

SCI绘图【1】-不同颜色表示密度和差异--密度图
参考资料:密度图(Density Plot) - 数据可视化图表 - 数字孪生百科 密度图是快速观察变量数值分布的有效方法之一。通常情况下,会根据两个变量将平面绘图区域分为非常多的子区域,之后以不同颜色表示落在该区域上样本的…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
