【C++高阶】掌握AVL树:构建与维护平衡二叉搜索树的艺术
📝个人主页🌹:Eternity._
⏩收录专栏⏪:C++ “ 登神长阶 ”
🤡往期回顾🤡:STL-> map与set
🌹🌹期待您的关注 🌹🌹



❀AVL树
- 📒1. AVL树的概念
- 📙2. AVL树节点的定义
- 📜3. AVL树的插入
- 📚4. AVL树的旋转
- 🌈右单旋
- 🌞左单旋
- 🌙左右双旋
- ⭐右左双旋
- 📝5. AVL树的验证
- 📘6. AVL树的缺陷
- 📖7. 总结
前言: 在数据结构的浩瀚海洋中,AVL树(Adelson-Velsky和Landis发明的树)以其独特的平衡机制和高效的搜索性能,成为了一颗璀璨的明星。它不仅解决了二叉搜索树在数据插入和删除时可能产生的失衡问题,更通过旋转操作,使得树的高度始终保持在一个相对较低的水平,从而保证了搜索的高效性
AVL树的学习并非一蹴而就。它需要我们深入理解其背后的数学原理和算法思想,掌握其插入、和旋转等操作的具体实现,并在实践中不断摸索和优化。只有经过这样的过程,我们才能真正掌握AVL树的精髓,并在实际项目中灵活运用
本篇我们将详细介绍AVL树的基本概念、性质、插入操作的具体实现、旋转操作的原理和技巧等内容!
让我们一起踏上学习 AVL树 的旅程,探索它带来的无尽可能!
📒1. AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
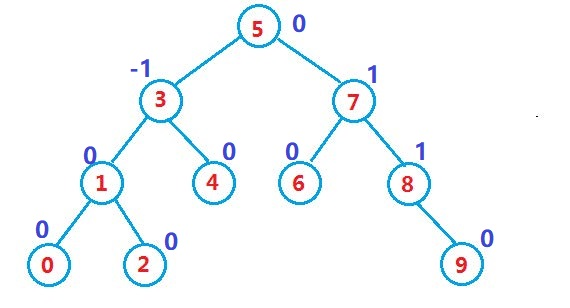
注意: 如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 O ( l o g 2 n ) O(log_2 n) O(log2n),搜索时间复杂度O( l o g 2 n log_2 n log2n)
📙2. AVL树节点的定义
AVL树节点的定义通常包含以下几个关键部分:
基本元素:
- _left:指向节点的左子节点的指针
- _right:指向节点的右子节点的指针
- _parent:指向节点的父节点的指针
- _kv:一个结构体或配对(pair),包含节点的键值(key)和值(value)。这取决于AVL树的具体用途,可能只包含键或包含键值对。
平衡因子(_bf):
- 一个整数,表示节点左子树和右子树的高度差。AVL树的性质要求任何节点的平衡因子的绝对值不超过1(-1, 0, 1)
构造函数:
- 初始化一个新节点时,通常需要一个构造函数,它接受一个键值对(或仅键),并设置节点的左子节点、右子节点、父节点和平衡因子(初始化为0)
节点定义示例(C++):
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left; // 该节点的左孩子AVLTreeNode<K, V>* _right; // 该节点的右孩子AVLTreeNode<K, V>* _parent; // 该节点的父亲pair<K, V> _kv; // pairint _bf; // balance factor 该节点的平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};
📜3. AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
在我们进行插入操作之前,我们先定义一个AVL树的类
AVL树定义示例(C++):
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:// 其他未实现的成员函数
private:Node* _root = nullptr;
};
cur插入后,parent的平衡因子一定需要调整
在插入之前,parent的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:
- 如果cur插入到parent的左侧,只需给parent的平衡因子-1即可
- 如果cur插入到parent的右侧,只需给parent的平衡因子+1即可
插入后,parent的平衡因子可能有三种情况:0,正负1, 正负2
- 如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整
成0,此时满足AVL树的性质,插入成功- 如果parent的平衡因子为正负1,说明插入前pParent的平衡因子一定为0,插入后被更
新成正负1,此时以parent为根的树的高度增加,需要继续向上更新- 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进
行旋转处理
AVL树的插入操作类似于我们之前二叉搜索树的插入,只不过AVL树的插入操作涉及到旋转操作,我们先演示一下它的全部代码
AVL树插入示例(C++):
bool Insert(const pair<K, V>& kv)
{// 当根节点为空时直接插入if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;// 寻找插入位置while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}// 链接新节点cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}// 更改平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;} if (parent->_bf == 0){break;}// 向上遍历,判断祖先是否受到影响else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}// 平衡出现问题,需要进行修理else if(parent->_bf == 2 || parent->_bf == -2){// 旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}return true;
}
📚4. AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,
使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
🌈右单旋
新节点插入较高左子树的左侧—左左:
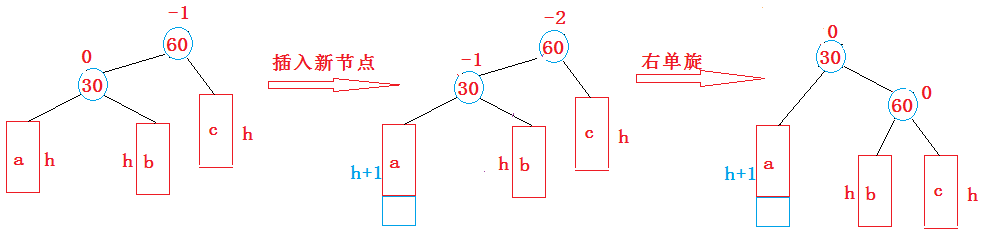
此处旋转是将30的右子树变成60的左子树,然后让60成为30的右子树
在旋转中有几点要注意:
30这个节点的右孩子可能不存在60这个节点可能是根节点,也可能是子树
如果是根节点,旋转完成后,要更新根节点
如果是子树,可能是某个节点的左子树,也可能是右子树
AVL树右单旋示例(C++):
void RotateR(Node* parent)
{// 定义parent的左孩子 和 parent的左孩子的右孩子Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}// 当旋转点是子树时,保留父亲节点Node* Parentparent = parent->_parent;subL->_right = parent;parent->_parent = subL;// 当旋转点是根时,跟新根节点if (_root == parent){_root = subL;subL->_parent = nullptr;}// 当旋转点是子树时,更新链接else{if (parent == Parentparent->_left){Parentparent->_left = subL;}else{Parentparent->_right = subL;}subL->_parent = Parentparent;}// 更新平衡因子为0parent->_bf = subL->_bf = 0;
}
🌞左单旋
新节点插入较高右子树的右侧—右右:
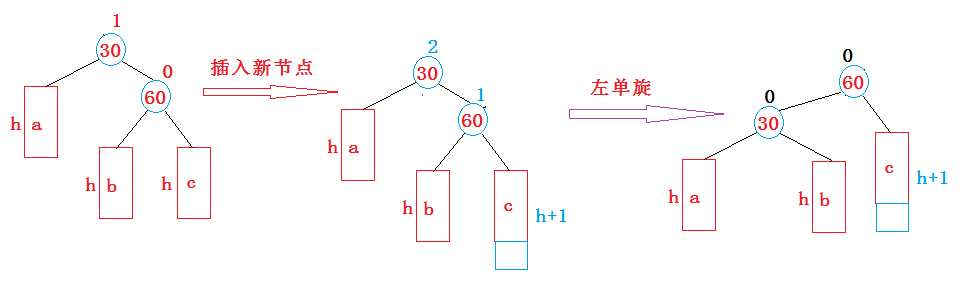
左单旋与单旋类似,所以我们直接来看代码
AVL树左单旋示例(C++):
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* Parentparent = parent->_parent;parent->_parent = subR;if (subRL){subRL->_parent = parent;}// 判断parent是不是根节点if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parent == Parentparent->_left){Parentparent->_left = subR;}else{Parentparent->_right = subR;}subR->_parent = Parentparent;}parent->_bf = subR->_bf = 0;
}
🌙左右双旋
新节点插入较高左子树的右侧—左右:
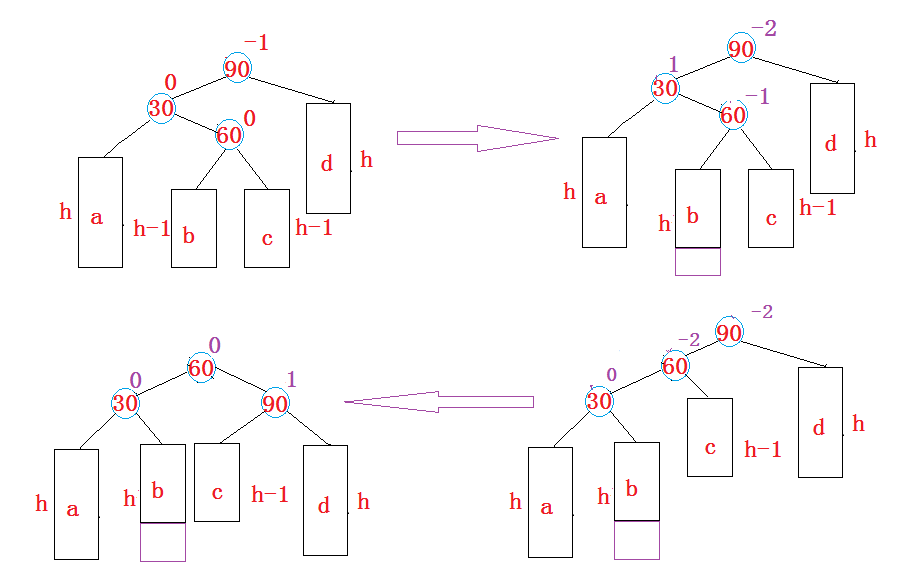
这里是将双旋变成单旋后再旋转,先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新
这里单旋可以复用上面讲的
AVL树左右双旋示例(C++):
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf; // 根据右子树的右孩子的平衡因子,判断旋转后的平衡因子情况// 复用单旋RotateL(parent->_left);RotateR(parent);// subLR就是新插入节点if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == 1){subLR->_bf = 0;parent->_bf = 0;subL->_bf = -1;}else if (bf == -1){subLR->_bf = 0;parent->_bf = 1;subL->_bf = 0;}else{assert(false);}
}
⭐右左双旋
新节点插入较高右子树的左侧—右左:
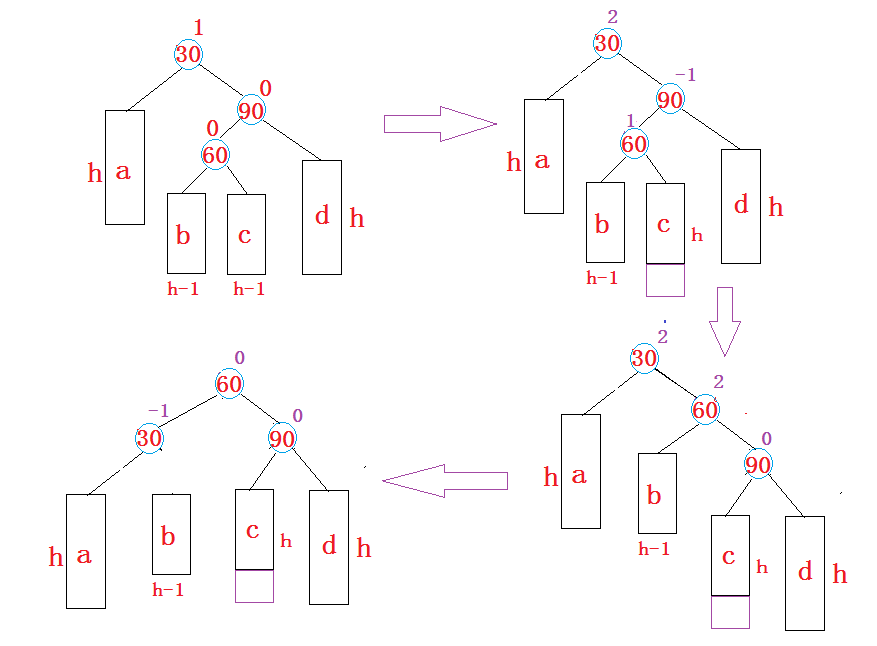
右左双旋和左右双旋类似,我们直接看代码
AVL树右左双旋示例(C++):
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;// 复用单旋RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else{assert(false);}
}
总结:
假如以parent为根的子树不平衡,即parent的平衡因子为2或者-2,分以下情况考虑
- parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根为subR
当subR的平衡因子为1时,执行左单旋
当subR的平衡因子为-1时,执行右左双旋- parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根为subL
当subL的平衡因子为-1是,执行右单旋
当subL的平衡因子为1时,执行左右双旋
旋转完成后,原parent为根的子树个高度降低,已经平衡,不需要再向上更新
📝5. AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
代码演示示例(C++):
// 中序遍历
void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);
}
验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
代码演示示例(C++):
bool IsBalance()
{return _IsBalance(_root);
}int _Height(Node* root)
{if (root == nullptr){return;}int rightHeight = _Height(root->_right);int leftHeight = _Height(root->_left);return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;
}bool _IsBalance(Node* root)
{if (root == nullptr){return true;}int rightHeight = _Height(root->_right);int leftHeight = _Height(root->_left);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子有误" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);
}
验证用例
int main()
{// 这里会进行双旋int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;return 0;
}
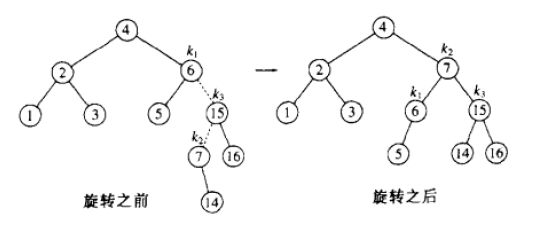
📘6. AVL树的缺陷
| 缺陷 | 原因 |
|---|---|
| 插入操作复杂 | 为了保持树的平衡,每次插入或删除节点时,AVL树可能需要进行多次旋转操作。具体来说,插入一个节点可能需要单旋转或双旋转来重新平衡树结构,而删除节点后可能需要从被删除节点到根节点这条路径上所有节点的平衡,旋转的量级最坏情况下为O(logN)。这增加了操作的复杂性并可能影响性能。 |
| 维护成本高 | 由于AVL树要求每个节点的左右子树高度差不超过1,因此需要频繁地检查和调整树的结构。这种严格的平衡要求导致了相对较高的维护成本,特别是在频繁进行插入和删除操作的情况下。 |
| 空间开销较大 | 虽然AVL树在查找效率上具有优势,但由于其需要频繁地进行旋转操作以维持平衡,这可能导致额外的空间开销。尤其是在处理大量数据时,这种开销可能会更加明显。 |
| 不适用于所有场景 | AVL树适用于查找操作远多于插入和删除操作的场景。如果在一个应用中插入和删除操作也非常频繁,那么AVL树可能不是最优选择,因为每次插入和删除都需要进行平衡调整,这会影响性能。 |
📖7. 总结
在深入探讨AVL树的旅程即将结束时,我们不禁为这种精妙的数据结构所折服。AVL树不仅以其高度的平衡性保证了高效的搜索、插入操作,而且它所蕴含的平衡维护机制也体现了计算机科学中的智慧与美
学习AVL树的过程,不仅是一次对数据结构知识的积累,更是一次对问题分析和解决能力的锻炼。我们学会了如何在插入和删除操作中通过旋转操作来保持树的平衡,这种动态调整的思想在软件开发中同样具有广泛的应用
AVL树的学习之旅虽然告一段落,但我们对数据结构和算法的探索永无止境。在未来的学习和工作中,我们将会遇到更多复杂的问题和挑战,但只要我们保持对知识的渴望和对问题的深入思考,就一定能够找到解决问题的钥匙
让我们以AVL树为起点,继续在数据结构和算法的海洋中遨游,不断挖掘计算机科学的奥秘,为未来的技术创新和进步贡献自己的力量。愿每一位学习者都能在求知的道路上不断前行,收获满满的智慧与快乐

希望本文能够为你提供有益的参考和启示,让我们一起在编程的道路上不断前行!
谢谢大家支持本篇到这里就结束了,祝大家天天开心!

相关文章:

【C++高阶】掌握AVL树:构建与维护平衡二叉搜索树的艺术
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C “ 登神长阶 ” 🤡往期回顾🤡:STL-> map与set 🌹🌹期待您的关注 🌹🌹 ❀AVL树 📒1. AVL树…...

机器学习-课程整理及初步介绍
简介: 机器学习是人工智能的一个分支,它使计算机系统能够从经验中学习并改进其在特定任务上的表现,而无需进行明确的编程。机器学习涉及多种算法和统计模型,它们可以从数据中学习规律,并做出预测或决策。机器学习的应用非常广泛&…...

北斗三号短报文通信终端 | 助力户外无网络场景作业
北斗三号短报文通信终端是一款专为户外无网络场景作业设计的先进通信工具,它依托于中国自主研发的北斗卫星导航系统,为用户在偏远地区或无网络覆盖区域提供了可靠的通信保障。以下是关于北斗三号短报文通信终端的详细介绍: 一、功能特点 北斗…...
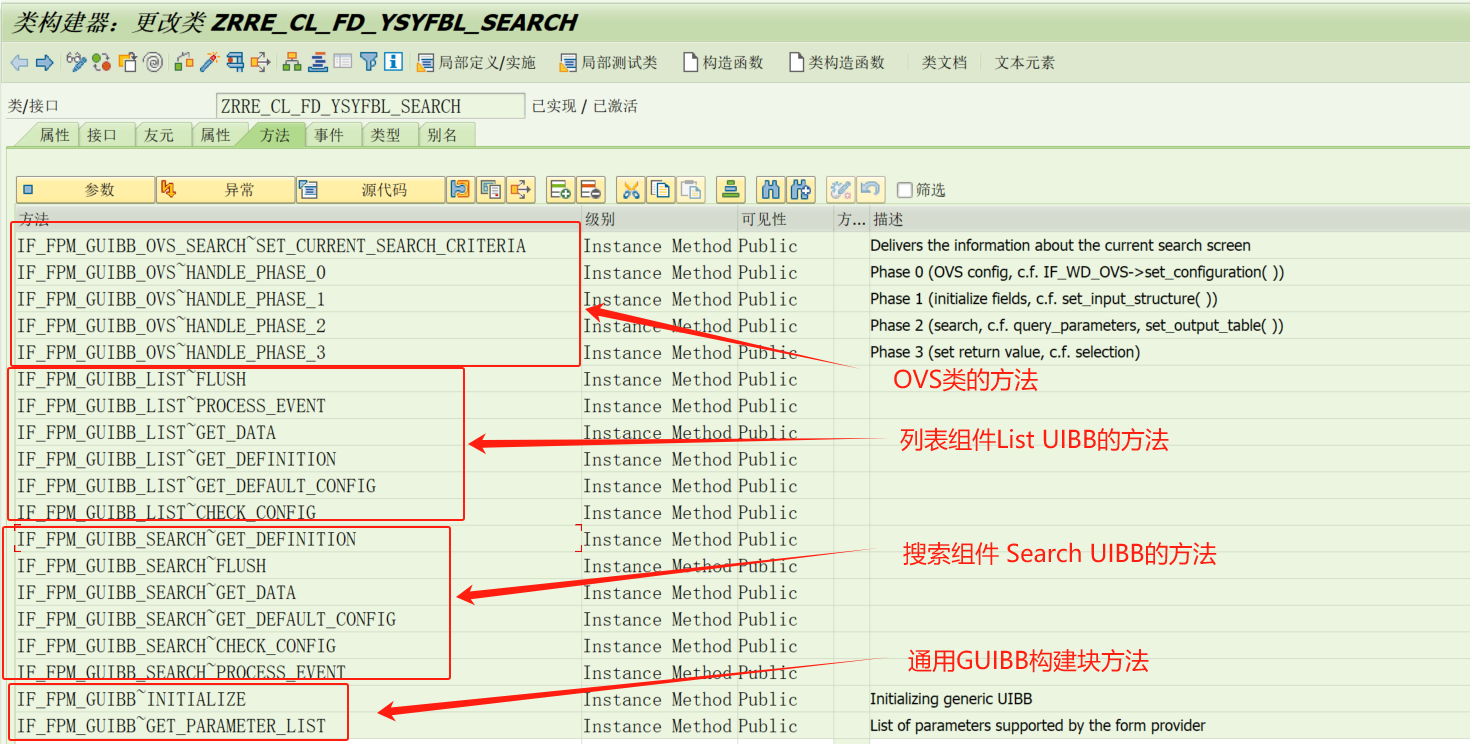
RERCS系统开发实战案例-Part05 FPM Application的Feeder Class搜索组件的实施
1、通过事务码 SE24对Feeder Class实施 1)接口页签的简单说明: ① IF_FPM_GUIBB:通用UI构建块,整个UIBB模块的基础接口; ② IF_FPM_GUIBB_SEARCH:通用搜索UI构建块,搜索组件UIBB的基础接口&…...
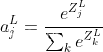
算法常见手写代码
1.NMS def py_cpu_nms(dets, thresh):"""Pure Python NMS baseline."""#x1、y1、x2、y2、以及score赋值x1 dets[:, 0]y1 dets[:, 1]x2 dets[:, 2]y2 dets[:, 3]scores dets[:, 4]#每一个检测框的面积areas (x2 - x1 1) * (y2 - y1 1)#按…...

数据结构9——排序
一、冒泡排序 冒泡排序(Bubble Sort),顾名思义,就是指越小的元素会经由交换慢慢“浮”到数列的顶端。 算法原理 从左到右,依次比较相邻的元素大小,更大的元素交换到右边;从第一组相邻元素比较…...

分布式锁实现方案-基于Redis实现的分布式锁
目录 一、基于Lua看门狗实现 1.1 缓存实体 1.2 延迟队列存储实体 1.3 分布式锁RedisDistributedLockWithDog 1.4 看门狗线程续期 1.5 测试类 1.6 测试结果 1.7 总结 二、RedLock分布式锁 2.1 Redlock分布式锁简介 2.2 RedLock测试例子 2.3 RedLock 加锁核心源码分析…...

MTK7628+MT7612 加PA定频数据
1、硬件型号TR726A5G121-DPA PC9.02.0017。如下所示: 2、WIFI5.8 AC模式 42(5120MHz)信道,80带宽 3、WIFI5.8 AC模式 38(5190MHz)信道,40带宽 4、WIFI5.8 AC模式 36(5180 MHz&…...

[信号与系统]关于双线性变换
前言 本文还是前置知识 双线性变换法 双线性变换法(Bilinear Transform)是一种用于将模拟滤波器转换为数字滤波器的方法。它通过将模拟域中的s平面上的传递函数映射到数字域中的z平面上的传递函数来实现这一转换。双线性变换法保证了频率响应在转换过…...
763. 划分字母区间
题目:给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。返回一个表示每个字符串片段的长度的列表…...

【PostgreSQL】AUTO_EXPLAIN - 慢速查询的日志执行计划
本文为云贝教育 刘峰 原创,请尊重知识产权,转发请注明出处,不接受任何抄袭、演绎和未经注明出处的转载。 一、介绍 在本文中,我们将了解 PostgreSQL AUTO_EXPLAIN功能的工作原理,以及为什么应该使用它来收集在生产系统…...

讯飞星火超自然语言合成的完整Demo
依赖文件和功能 requirements.txt 该文件列出了所需的依赖包。 data.py 定义了应用的配置信息,如APPId,APIKey,APISecret等。包含请求数据和请求URL。 main.py 主程序,设置了WebSocket连接,定义了处理消息的各个回调函…...
)
封装一个上拉加载的组件(无限滚动)
一、封装 1.这个是在vue3环境下的封装 2.整体思路: 2.1传入一个elRef,其实就是一个使用页面的ref。 2.2也可以不传elRef,则默认滚动的是window。 import { onMounted, onUnmounted, ref } from vue; import { throttle } from underscore;ex…...
)
WHAT - 高性能和内存安全的 Rust(二)
目录 1. 所有权(Ownership)2. 借用(Borrowing)不可变借用可变借用 3. 可变性(Mutability)4. 作用域(Scope)综合示例 了解 Rust 的所有权(ownership)、借用&am…...

办理河南建筑工程乙级设计资质的流程与要点
办理河南建筑工程乙级设计资质的流程与要点 办理河南建筑工程乙级设计资质的流程与要点主要包括以下几个方面: 流程: 工商注册与资质规划:确保企业具有独立法人资格,完成工商注册,并明确乙级设计资质的具体要求&…...

分类算法和回归算法区别
分类算法和回归算法在机器学习中扮演着不同的角色,它们的主要区别体现在输出类型、应用场景以及算法目标上。以下是对两者区别和使用场景的详细分析: 一、区别 1.输出类型: 分类算法:输出是离散的类别标签,通常表示为…...
利用Frp实现内网穿透(docker实现)
文章目录 1、WSL子系统配置2、腾讯云服务器安装frps2.1、创建配置文件2.2 、创建frps容器 3、WSL2子系统Centos服务器安装frpc服务3.1、安装docker3.2、创建配置文件3.3 、创建frpc容器 4、WSL2子系统Centos服务器安装nginx服务 环境配置:一台公网服务器(…...

怎么用Excel生成标签打印模板,自动生成二维码
环境: EXCEL2021 16.0 问题描述: 怎么用excel生成标签打印模板自动生成二维码 解决方案: 在Excel中生成标签打印模板并自动生成二维码,可以通过以下几个步骤完成: 1. 准备数据 首先,确保你的Excel表…...
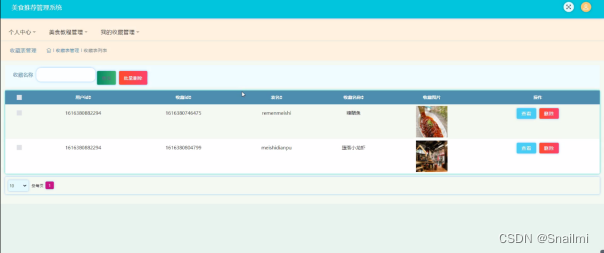
java基于ssm+jsp 美食推荐管理系统
1前台首页功能模块 美食推荐管理系统,在系统首页可以查看首页、热门美食、美食教程、美食店铺、美食社区、美食资讯、我的、跳转到后台等内容,如图1所示。 图1前台首页功能界面图 用户注册,在注册页面可以填写用户名、密码、姓名、联系电话等…...
数据分析:置换检验Permutation Test
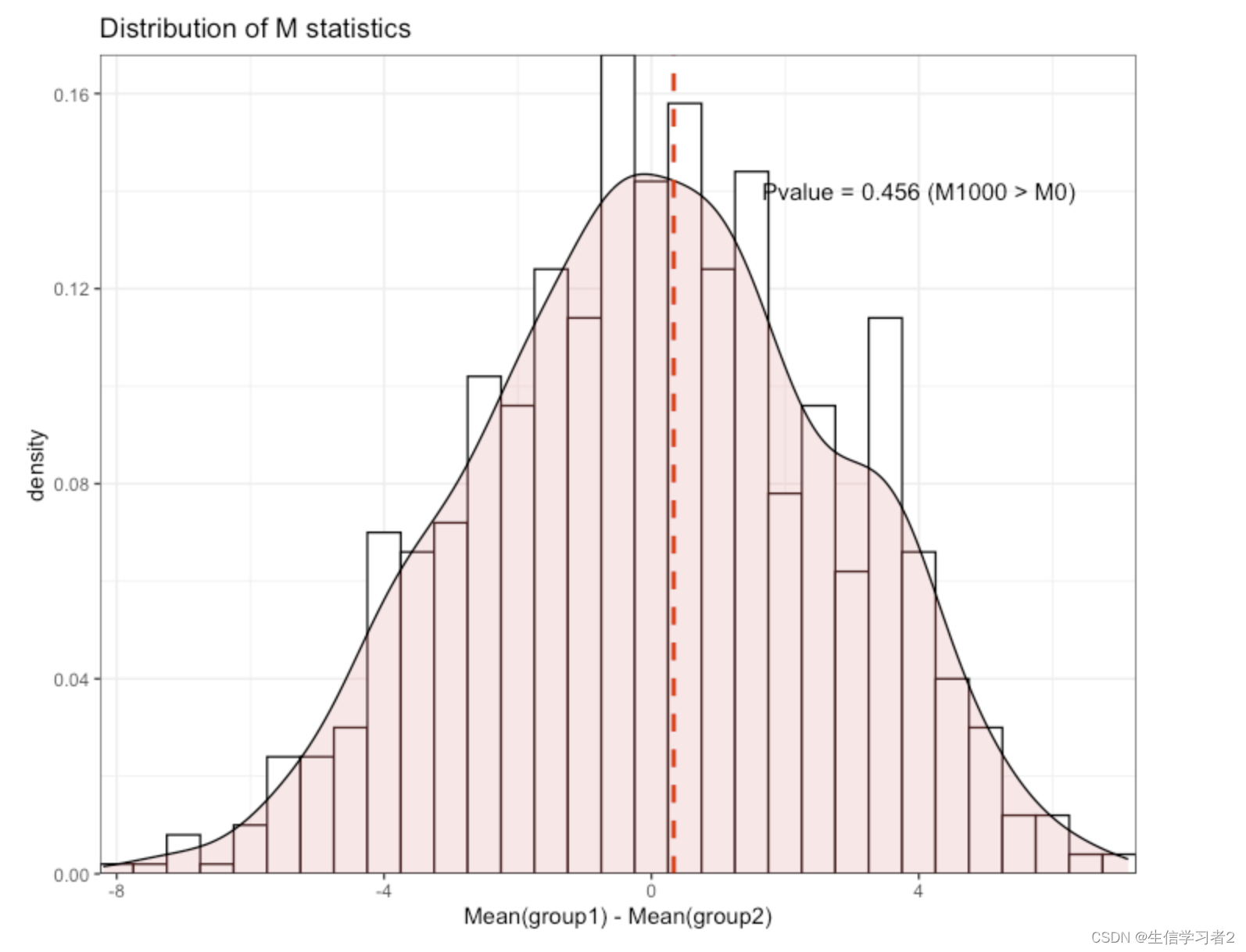
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 置换检验是一种非参数统计方法,它不依赖于数据的分布形态,因此特别适…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
