【数据结构】二叉树相关OJ题
文章目录
- 一、单值二叉树
- 二、检查两颗树是否相同
- 三、判断一棵树是否为另一颗树的子树
- 四、对称二叉树
- 五、二叉树的前序遍历
- 六、二叉树中序遍历
- 七、二叉树的后序遍历
- 八、二叉树的构建及遍历
一、单值二叉树
单值二叉树
题目描述
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树,只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例

思路分析
一棵树的所有节点都有相同的值,当且仅当对于树上的每一条边的两个端点,它们都有相同的值(这样根据传递性,所有节点都有相同的值)
因此,我们可以对树进行一次深度优先搜索,当搜索到节点root时,我们检查root的左孩子和右孩子是否相同,不相同则返回false,直到检查了所有的节点,所有我们就可以进行递归遍历,每次比较根节点和左右孩子的val值是否相等,不相等就返回false,然后递归比较左子树和右子树。
【注意】我们比较的条件应该是不相等,因为不相等就可以直接返回,而相等还要继续比较
代码实现
bool isUnivalTree(struct TreeNode* root)
{// 根节点为空返回trueif (root == NULL)return true;// 左子树存在但是不相等则返回falseif (root->left && root->val != root->left->val)return false;// 右子树存在但是不相等则返回falseif (root->right && root->val != root->right->val)return false;// 继续递归 左右子树return isUnivalTree(root->left) && isUnivalTree(root->right);
}
二、检查两颗树是否相同
题目链接
检查两颗树是否相同
题目描述
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例

思路分析
如果两个二叉树都为空,则两个二叉树相同。如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同,如果两个二叉树都不为空,那么首先判断它们的根节点的值是否相同,若不相同则两个二叉树一定不同,若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程,因此可以使用深度优先搜索,递归地判断两个二叉树是否相同。
代码实现
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{// 如果根节点都为NULL则返回tureif (p == NULL && q == NULL)return true;// 运行到这里,都不为空,则下面判断的情况为只有一个为空,另一个不为空,所以返回falseif (p == NULL || q == NULL)return false;// 都不为空但是值不相等返回falseif (p->val != q->val)return false;// 继续比较左右子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
三、判断一棵树是否为另一颗树的子树
题目链接
判断一棵树是否为另一颗树的子树
题目描述
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树
示例

思路分析
由于root和subRoot中可能含有一个和多个值相同的节点,所以判断不相等的时候,又要返回原来的根节点,所以我们可以这道题利用上一题的代码,我们的思路为不断的比较root这棵树以每一个节点作为根节点,判断是否和subRoot相等,相等就返回true,所以节点都变量之后都没有相等的树就返回false.
代码实现
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{// 如果根节点都为NULL则返回tureif (p == NULL && q == NULL)return true;// 运行到这里,都不为空,则下面判断的情况为只有一个为空,另一个不为空,所以返回falseif (p == NULL || q == NULL)return false;// 都不为空但是值不相等返回falseif (p->val != q->val)return false;// 继续比较左右子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {if (root == NULL){return false;}if (isSameTree(root, subRoot)){return true;}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);}

四、对称二叉树
题目链接
对称二叉树
题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称
示例

思路分析
这道题和判断两棵树是否相等的思路一致,只是有一些细节有所不同。对称二叉树是最左边和最右边的节点相同,所以我们就可以拿第一棵树的左子树和第二棵树的右子树进行比较,拿第一棵树的右子树和第二棵树的左子树进行比较,不相等就返回false,相等就继续比较,直到所有节点都相等,所以我们就可以对检查两颗是否相同的代码进行修改即可,即对其递归代码中的参数进行调整
return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);
代码实现
//判断两颗子树是否对称
bool isSameTree(struct TreeNode* p,struct TreeNode* q)
{if(p==NULL&&q==NULL){return true;}// 当两棵树中只有一棵树的节点为NULL时,节点数量不相等,直接返回falseif(p==NULL||q==NULL){return false;}// 检查节点的值是否相等if(p->val!=q->val){return false;}// 检查左右子树是否对称return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){return isSameTree(root->left,root->right);
}

五、二叉树的前序遍历
题目链接
二叉树的前序遍历
题目描述
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例

思路分析
二叉树的前序遍历我们已经非常熟悉,这里我提出两点需要注意的地方:
1.由于二叉树的节点数是未知的,为了不浪费空间,我们可以先求出二叉树的节点数,然后开辟对应大小的空间
2.由于数据存储在一个数组中,所以我们需要一个变量i来控制数组的下标,由于在递归调用的过程中对形参的改变不会改变影响实参,所以这里我们需要传递i的地址,通过指针来控制i的增长
代码实现
// 计算节点个数
int TreeSize(struct TreeNode* root)
{if (root == NULL)return 0;// 左子树的节点个数+右节点的个数+1return TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 前序遍历并存入数组中
void preorder(struct TreeNode* root, int* a, int* pi)
{if (root == NULL)return;// 先遍历根,再访问左子树,左后访问右子树a[*pi] = root->val;(*pi)++;preorder(root->left, a, pi);preorder(root->right, a, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{// 求二叉树的节点个数int size = TreeSize(root);// 开辟同等大小的空间int* a = (int*)malloc(sizeof(int) * size);int i = 0;//前序遍历preorder(root, a, &i);*returnSize = size;return a;
}

六、二叉树中序遍历
题目链接
二叉树中序遍历
题目描述
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例

二叉树的中序遍历和前序遍历一样,只是访问节点的顺序不同
代码实现
// 计算节点个数
int TreeSize(struct TreeNode* root)
{if (root == NULL)return 0;// 左子树的节点个数+右节点的个数+1return TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 前序遍历并存入数组中
void inorder(struct TreeNode* root, int* a, int* pi)
{if (root == NULL)return;// 先遍历左子树,再访问根节点,左后访问右子树inorder(root->left, a, pi);a[*pi] = root->val;(*pi)++;inorder(root->right, a, pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{// 求二叉树的节点个数int size = TreeSize(root);// 开辟同等大小的空间int* a = (int*)malloc(sizeof(int) * size);int i = 0;//中序遍历inorder(root, a, &i);*returnSize = size;return a;
}

七、二叉树的后序遍历
题目链接
二叉树的后序遍历
题目描述
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例

思路分析
二叉树的后序遍历和前序遍历,中序遍历一样,只是访问节点的顺序不同
代码实现
代码实现
// 计算节点个数
int TreeSize(struct TreeNode* root)
{if (root == NULL)return 0;// 左子树的节点个数+右节点的个数+1return TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 后序遍历并存入数组中
void postorder(struct TreeNode* root, int* a, int* pi)
{if (root == NULL)return;// 先遍历左子树,再访问右子树,左后访问根节点postorder(root->left, a, pi);postorder(root->right, a, pi);a[*pi] = root->val;(*pi)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{// 求二叉树的节点个数int size = TreeSize(root);int* a = (int*)malloc(sizeof(int) * size);int i = 0;// 后续遍历postorder(root, a, &i);*returnSize = size;return a;
}

八、二叉树的构建及遍历
题目链接
二叉树的构建及遍历
题目描述
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
示例

思路分析
这道题目是前序建立二叉树和中序遍历,我们写成两个子函数即可,对于二叉树的创建,字符为‘#’说明节点为空,我们直接返回即可,然后依次递归创建节点即可
代码实现
#include <stdio.h>
#include <stdlib.h>// 符号和结构的定义
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;// 构建二叉树
BTNode* BTreeCreate(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}// 创建根节点BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL) {perror("malloc fail");exit(-1);}root->data = a[*pi];(*pi)++;// 创建左子树和右子树root->left = BTreeCreate(a, pi);root->right = BTreeCreate(a, pi);return root;
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){return;}// 先访问左子树,再访问根节点,最后访问右子树InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}int main()
{char str[100];scanf("%s", str);// 创建二叉树int i = 0;BTNode* root = BTreeCreate(str, &i);// 二叉树的中序遍历InOrder(root);return 0;
}

相关文章:

【数据结构】二叉树相关OJ题
文章目录一、单值二叉树二、检查两颗树是否相同三、判断一棵树是否为另一颗树的子树四、对称二叉树五、二叉树的前序遍历六、二叉树中序遍历七、二叉树的后序遍历八、二叉树的构建及遍历一、单值二叉树 单值二叉树 题目描述 如果二叉树每个节点都具有相同的值,那…...
Windows安装Hadoop
当初搭建Hadoop、Hive、HBase、Flink等这些没有截图写文,今为分享特重装。下载Hadoop下载地址:https://mirrors.tuna.tsinghua.edu.cn/apache/hadoop/以管理员身份运行cmd切换到所在目录执行start winrar x -y hadoop-3.3.4.tar.gz,解压。配置…...
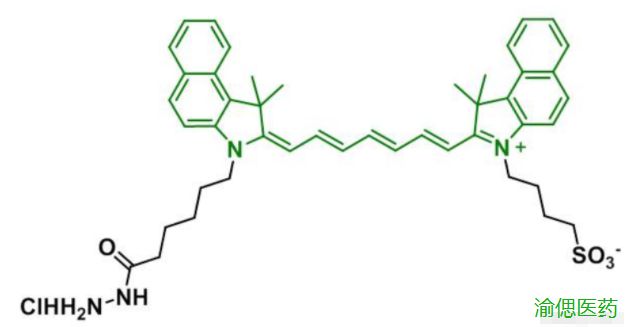
ICG-Hydrazide,吲哚菁绿-酰肼,ICG-HZ结构式,溶于二氯甲烷等部分有机溶剂,
ICG-Hydrazide,吲哚菁绿-酰肼 中文名称:吲哚菁绿-酰肼 英文名称:ICG-Hydrazide 英文别名:ICG-HZ 性状:粉末或固体 溶剂:溶于二氯甲烷等部分有机溶剂 稳定性:-20℃密封保存、置阴凉干燥处、防潮 分子…...
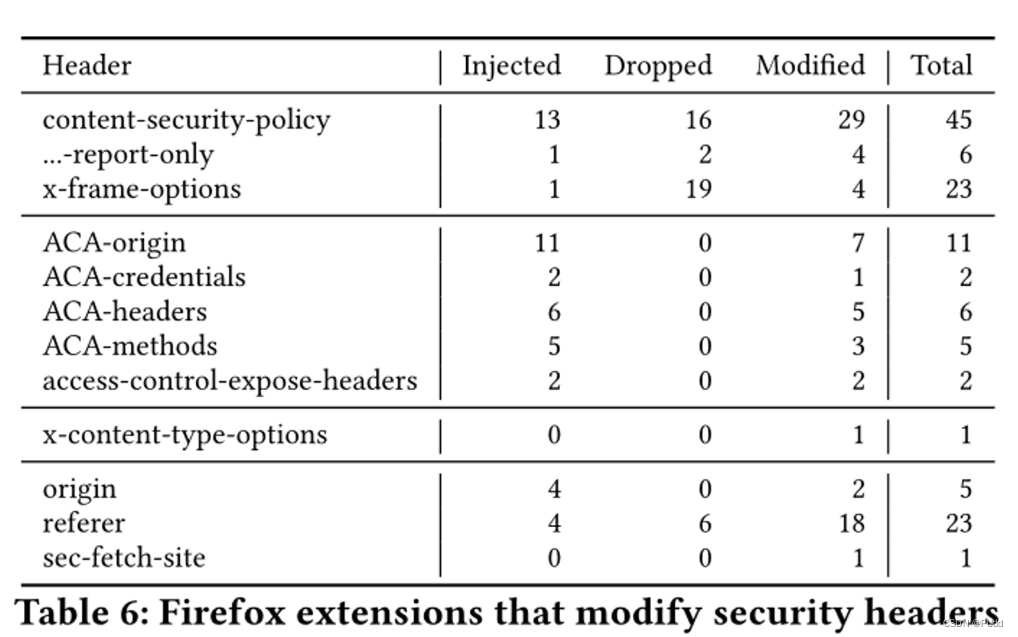
【论文阅读】浏览器扩展危害-Helping or Hindering? How Browser Extensions Undermine Security
本文来源于ACM CCS 2022; https://dl.acm.org/doi/10.1145/3548606.3560685 摘要 “浏览器扩展”是轻量级的浏览器附加组件,使用各个浏览器特定的功能丰富的JavaScript api,为用户提供了额外的Web客户端功能,如改进网站外观和与…...
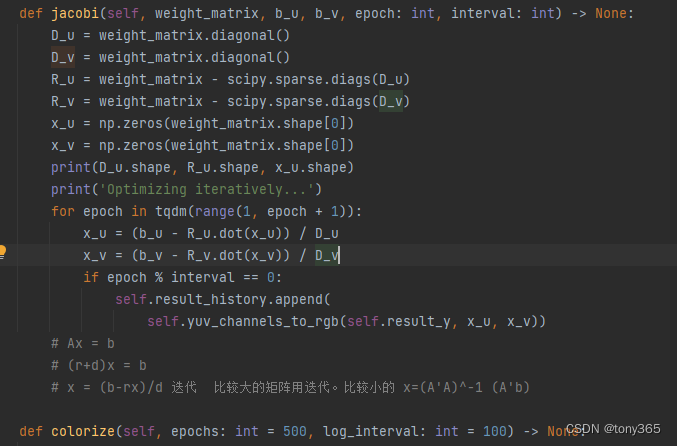
线性和非线性最小二乘问题的常见解法总结
线性和非线性最小二乘问题的各种解法 先看这篇博客,非常好:线性和非线性最小二乘问题的各种解法 1. 线性最小二乘问题有最优解 但是面对大型稀疏矩阵的时候使用迭代法效率更好。 迭代法 有Jacobi迭代法、 Seidel迭代法及Sor法 【数值分析】Jacobi、Se…...

数据库知识点
数据库是指按照一定规则存储、组织和管理数据的系统。在现代化的信息化社会中,数据库已经成为了各种应用系统中不可或缺的一部分。因此,对于数据库的知识掌握不仅是计算机专业人员必备的技能,也是各个行业从业者必须具备的基本素质之一。 数…...

Maven打包构建Docker镜像并推送到仓库
Maven打包构建Docker镜像并推送到仓库 文章目录Maven打包构建Docker镜像并推送到仓库一,服务器Docker配置二,本地项目maven配置2.1 pom.xml2.2 dockerfile2.3 验证2.4 统一dockerfile对于开发完成的服务要发布至服务器Docker时,我刚学习了解D…...

TypeScript 基础学习之泛型和 extends 关键字
越来越多的团队开始使用 TS 写工程项目, TS 的优缺点也不在此赘述,相信大家都听的很多了。平时对 TS 说了解,仔细思考了解的也不深,借机重新看了 TS 文档,边学习边分享,提升对 TS 的认知的同时,…...
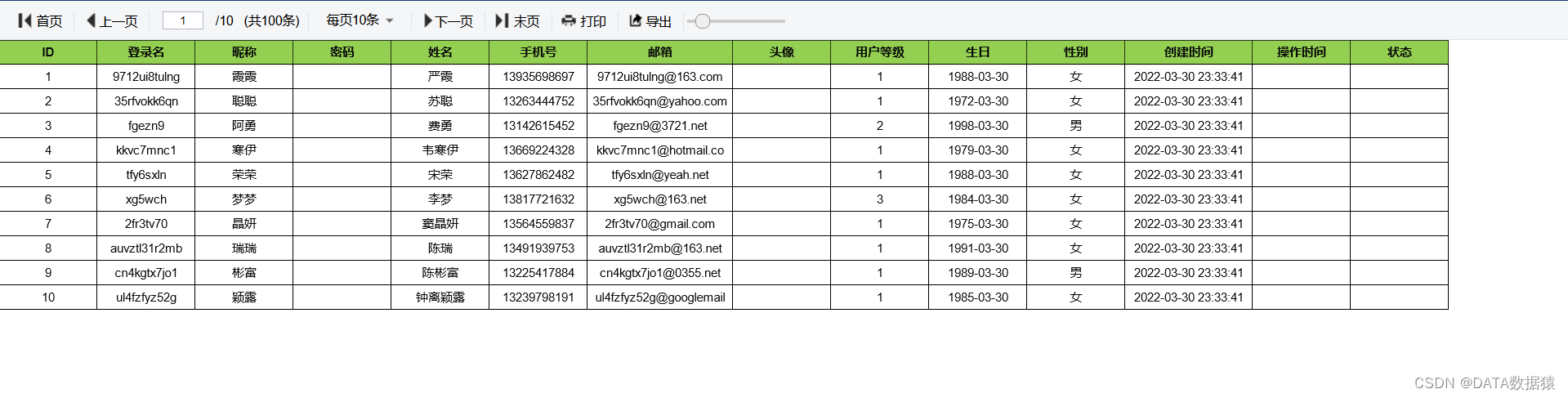
《数据分析-JiMuReport04》JiMuReport报表设计入门介绍-页面优化
报表设计 2 页面优化 如上图所示的报表,仅仅是展示数据,不过这样看起来似乎太草率了,所以再优化一下吧 保存报表后,在积木报表中就可以看到对应的报表文件 此时我们如果还需要编辑报表,就点击这个报表即可 2.1 居中…...
带头双向循环链表及链表总结
1、链表种类大全 1、链表严格来说可能用2*2*28种结构,从是否带头,是否循环,是否双向三个角度区分。 2、无头单向循环链表一般不会在实际运用中直接存储数据,而会作为某些更复杂结构的一个子结构,毕竟它只在头插、头删…...
MySQL是如何基于各种规则去优化执行计划的?(中))
(八十)MySQL是如何基于各种规则去优化执行计划的?(中)
今天我们来讲一下子查询是如何执行的,以及他的执行计划是如何优化的。比如说类似于下面的SQL语句: select * from t1 where x1 (select x1 from t2 where idxxx) 这就是一个典型的子查询 也就是说上面的SQL语句在执行的时候,其实会被拆分为…...

第一章:命题与命题公式
1.命题与命题联结词 1.命题与命题的表示 1. 命题 由一个或几个已知的前提,推导出来一个未知的结论的思维过程称为推理,推理的基本要素就是表达这些前提的一些陈述句,可以将这些陈述句理解为命题。 (1)地球是行星 (2)8不是素数 (3)1 + 2 = 22. 命题真值 一个陈述句不…...
,操作符重载)
c/c++开发,无可避免的操作符operator(篇一),操作符重载
一、操作符号重载 虽然c/c内置了大量各类操作符,开发者可以很方便将其应用数学运算、成员访问、类型转换、内存分配等执行语句中,但很多时候,也需要根据项目应用需要,通过操作符重载,能够针对类类型的操作数定义不同的…...

【7.MySQL行格式存储】
1.MySQL数据存放文件 我们每创建一个 database(数据库) 都会在 /var/lib/mysql/ 目录里面创建一个以 database 为名的目录,创建一个student表 [rootxiaodainiao ~]#ls /var/lib/mysql/my_test db.opt student.frm student.ibddb.opt:用…...

【Linux】线程实例 | 简单线程池
今天来写一个简单版本的线程池 1.啥是线程池 池塘,顾名思义,线程池就是一个有很多线程的容器。 我们只需要把任务交到这个线程的池子里面,其就能帮我们多线程执行任务,计算出结果。 与阻塞队列不同的是,线程池中内有…...

ATAC-seq 数据分析实战
文章目录一、 ATAC-seq原理和基础知识1. ATAC-seq原理2. Tn5转座子1. 转座概念2. 参与分子1. 转座子(1) 简化的转座子结构(2) Tn5转座子的结构2. 转座酶3. 转座过程二、数据比对和过滤一、 ATAC-seq原理和基础知识 1. ATAC-seq原…...
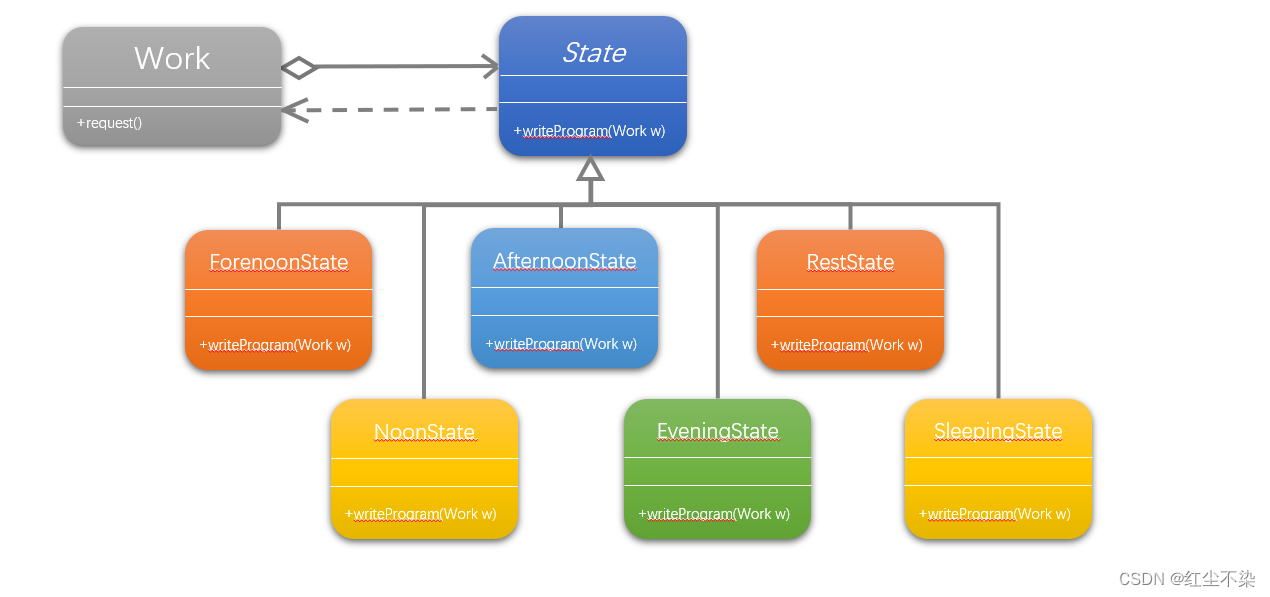
设计模式-第13章(状态模式)
状态模式状态模式状态模式的好处和用处工作状态状态模式 状态模式(State),当一个对象的内在状态改变时允许改变其行为,这个对象看起来像是改变了其类。 状态模式主要解决的是当控制一个对象状态转换的条件表达式过于复杂时的情况…...
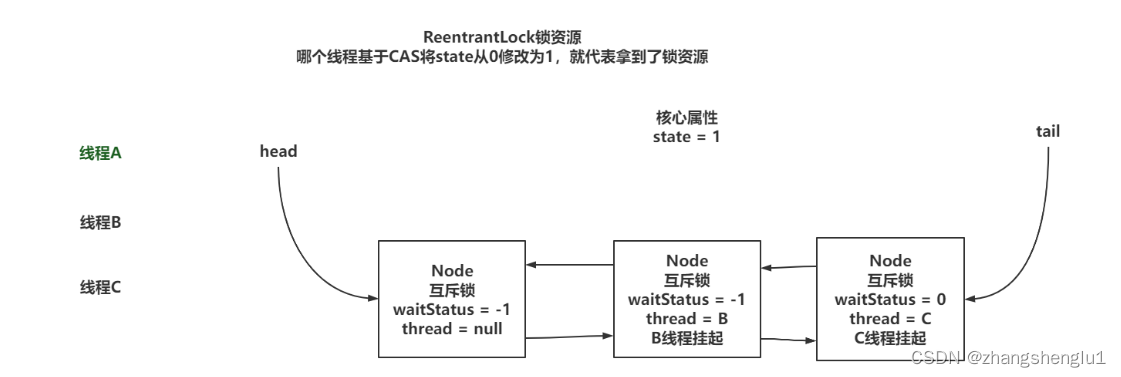
ReentrantLock源码分析(一)加锁流程分析
一、ReetrantLock的使用示例 static ReentrantLock lock new ReentrantLock(); public static void main(String[] args) throws InterruptedException { new Thread(ClassLayOutTest::reentrantLockDemo, "threadA").start(); Thread.sleep(1000);…...
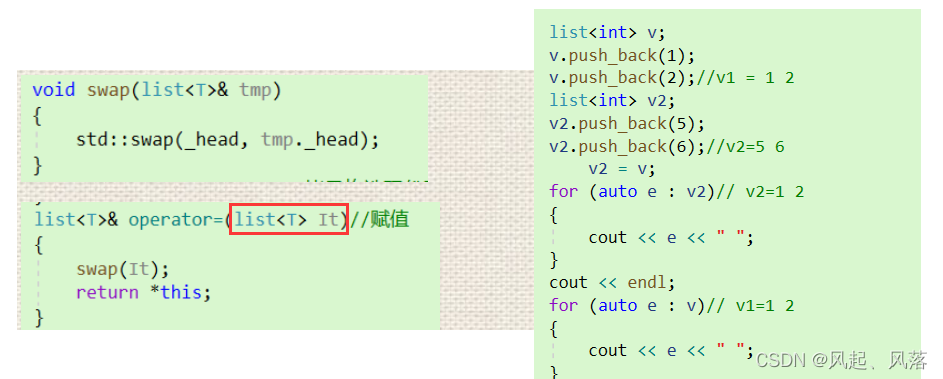
【C++】list的模拟实现
文章目录1.list 底层2. list的模拟实现1. list_node 类设计2. list类如何调用类型3 .push_back(正常实现)4. 迭代器的实现第一个模板参数Tconst迭代器第二个模板参数Ref第三个模板参数Ptr对list封装的理解5. insert6.push_back与 push_front(复用)7. erase8. pop_back与pop_fro…...

Python连接es笔记三之es更新操作
这一篇笔记介绍如何使用 Python 对数据进行更新操作。 对于 es 的更新的操作,不用到 Search() 方法,而是直接使用 es 的连接加上相应的函数来操作,本篇笔记目录如下: 获取连接update()update_by_query()批量更新UpdateByQuery()…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
