排序算法系列一:选择排序、插入排序 与 希尔排序
目录
零、说在前面
一、理论部分
1.1:选择排序
1.1.1:算法解读:
1.1.2:时间复杂度
1.1.3:优缺点:
1.1.4:代码:
1.2:插入排序
1.2.1:算法解读:
1.2.2:时间复杂度
1.2.3:优缺点:
1.2.4:代码:
1.3:希尔排序
1.3.1:算法解读:
1.3.2:时间复杂度
1.3.3:优缺点:
1.3.4:代码:
二、对比
2.1:选择与冒泡
2.2:插入与选择
2.3:插入与希尔
零、说在前面
本文是一个系列,入口请移步这里
一、理论部分
1.1:选择排序
1.1.1:算法解读:
使用二分法和插入排序两种算法的思想来实现。流程分为“拆分”、“合并”两大部分,前者就是普通的二分思想,将一个数组拆成n个子组;后者是在每个子组内部用插入法排序,在子组间定义一个辅助数组和三个指针,用辅助数组搭配指针选数进行排序,再将两个子组合并;最终将所有子组合并成一个有序的数组。
1.1.2:时间复杂度
由于该算法使用了双层for循环,分别涉及到 (N-1)*N/2 次的比较和 (N-1)*N/2 次的交换
因此时间复杂度 是 (N-1)*N,即 -N,故而时间复杂度为 O(
)
在最优与最坏情况,二分操作耗时不会节约、归并比较阶段操作耗时不会节约,因此遍历的数据量不变,,因此固定为O()
1.1.3:优缺点:
受该算法的时间复杂度所限,在小数据量时有不错的效率,不适用于大量数据排序。
1.1.4:代码:
/*** date: 2024-06-23* author: dark* description: 选择排序算法(由小到大)*/
public class Selection {/*** 逻辑步骤:1:接受一个数组,从左向右循环遍历数组中每个元素,并将每轮循环得到的最小元素置于本轮循环的起始位置* @param arrays*/public void selectSort(Integer[] arrays){/*** 定义临时变量 和 数组长度*/Integer temp = 0 , arrayLength = arrays.length ;/*** 从左向右遍历数组元素,获取并将每轮遍历的最小元素置于本轮循环的起始位置。*/for (int i = 0; i < arrayLength; i++) {for (int j = i+1; j < arrayLength; j++) {if(arrays[i] > arrays[j]){temp = arrays[i];arrays[i] = arrays[j];arrays[j] = temp;}}}}
}1.2:插入排序
1.2.1:算法解读:
将数组看做左侧有序右侧无序的两部分。初始状态以数组最左侧的一个数据作为已排序组。逐个使用未排序组元素,从右向左地与已排序组元素逐个对比,若未排序的数据小于已排序数据则交换,否则使用未排序组的下一个元素重复上面的操作,直至整个数组有序。
1.2.2:时间复杂度
由于该算法使用了双层for循环,分别涉及到 (N-1)*N/2 次的比较和 (N-1)*N/2 次的交换
因此时间复杂度 是 (N-1)*N,即 -N,故而时间复杂度为 O(
)
最优情况下数组有序,时间复杂度为 O(N),最坏情况下数据倒序,,时间复杂度为O(),平均时间复杂度为 O(
) (推导过程复杂,需要考虑各种情况的加权平均,因此略过)
1.2.3:优缺点:
同选择排序。
1.2.4:代码:
/*** date: 2024-06-22* author: dark* description: 插入排序算法(由小到大)*/
public class Insertion {/*** 逻辑步骤:1:接受一个数组,初始状态以其首元素作为“有序组”,其余元素作为“无序组”,并记录有序组和无序组首元素的坐标* 2:遍历无序组,每轮遍历只取无序组左侧首元素,以从右向左的顺序与有序组中的各个元素进行比对* 当无需组首元素小于有序组元素,交换二者位置,直至有序组达到首元素或有序组再无元素大于无序组首元素,退出遍历* 3:将无序组首元素坐标右移,重复步骤2的操作,直至无序组中没有元素。* @param arrays*/public void insertionSort(Integer[] arrays){/*** 定义临时交换变量*/Integer temp;/*** 遍历无序组*/for(int i= 1; i < arrays.length; i++){/*** 将无序组的首元素从右向左逐个与有序组比对,若首元素更小则交换,直至首元素大于有序组某元素或到达有序组首位* i 代表无序组的首元素,j 代表有序组的末元素*/for (int j = i-1; j >= 0; j--) {if(arrays[j+1] < arrays[j]){temp = arrays[j+1];arrays[j+1] = arrays[j];arrays[j] = temp;}else{break;}}}}
}1.3:希尔排序
1.3.1:算法解读:
借鉴了分治法的思想,在插入的基础上做了优化。对原数组进行多轮分组,组数据量随着轮次的递增而倍增。同时在每轮都对组内数据进行插入排序,使组数据趋势有序,这为最终一次使用插入排序减少了数据交换的次数。
1.3.2:时间复杂度
因为用到了分治思想,因此时间复杂度除了与数据量有关,还与遍历次数(即对数据量二分次数 logN )有关,因此时间复杂度为 O(N logN)
无论最优还是最差情况,遍历的数据量及遍历轮次不变,因此时间复杂度恒定 O(N logN)。而且不会因数据完全有序而减少过多的遍历过程。可以用1~8和8~1 验算一次,执行次数基本无差
1.3.3:优缺点:
因为用到分治思想,故在大数据量情况下排序表现较好。
1.3.4:代码:
/*** date: 2024-06-22* author: dark* description: 希尔排序算法(由小到大)*/
public class Shell {/*** 逻辑步骤:1:接受一个数组,定义分组步长,设初始值为1,并不断用 步长*2+1 的结果与数组长度比对,直至大于后者作为步长的实际值* 2:从数组首元素开始,将与之距离为步长倍数的所有元素视为一组,对这组元素按照插入排序法排序。* 3:按上述方法逐个处理整个数组的所有元素* 4:将步长减半,重复第2、3步,直至步长减为1。* @param arrays*/public void shellSort(Integer[] arrays){/*** 定义步长、数组长度、临时变量*/int stepLength = 1;int arrLength = arrays.length;int temp = 0;/*** 确定stepLength 的初始值*/while (stepLength <= arrLength / 2){stepLength = stepLength * 2 + 1;}/*** 逐渐缩小步长,重复执行小组插入排序逻辑*/while(stepLength >= 1){/*** 用以 stepLength 为首元素的子组作为无序组,以 j-stepLength 为首元素的子组作为有序组。执行插入排序*/for (int j = stepLength; j < arrLength; j+=stepLength) {for (int k = j-stepLength; k >=0; k-=stepLength) {if(arrays[k+stepLength] < arrays[k]){temp = arrays[k];arrays[k] = arrays[k+stepLength];arrays[k+stepLength] = temp;}else{break;}}}stepLength /= 2;}}
}二、对比
2.1:选择与冒泡
二者核心算法接近,区别在于后者将每轮循环中得到的最小值规整到了固定位置,有整理收纳的思想在里面。
2.2:插入与选择
选择排序受其逻辑制约,无论如何都要把本轮剩余的元素都遍历一次,因此其时间复杂度是固定的 O(N平方),但插入排序由于有序组数据的规律性,因此其时间复杂度在最优情况下可以达到O(N)(即初始有序),最坏情况下是O(N平方)(即逆序)
2.3:插入与希尔
后者通过多次小范围插排,将数据尽可能的规整。我测试生成9万、20万和40万条随机数,然后分别使用希尔和插入排序分别对这些数据的副本进行排序。对比结果前两次希尔稍快(60%和80%左右),第三次希尔略慢(103%左右)。可见,随着数据量的增大,多次插排的时间代价带来的时间损耗就比较明显了。
相关文章:
排序算法系列一:选择排序、插入排序 与 希尔排序
目录 零、说在前面 一、理论部分 1.1:选择排序 1.1.1:算法解读: 1.1.2:时间复杂度 1.1.3:优缺点: 1.1.4:代码: 1.2:插入排序 1.2.1:算法解读&#x…...

【快速排序】| 详解快速排序 力扣912
🎗️ 主页:小夜时雨 🎗️专栏:快速排序 🎗️如何活着,是我找寻的方向 目录 1. 题目解析2. 代码 1. 题目解析 题目链接: https://leetcode.cn/problems/sort-an-array/ 我们上道题讲过快速排序的核心代码&a…...
游戏推荐: 植物大战僵尸杂交版
下载地址网上一搜就有. 安装就能玩. 2是显血. 4显示植物血, 5是加速. 都是左手主键盘的按钮, 再按是取消. 比较刺激: ps: 设置里面还能打开自动收集阳光和金币....

微调和rag的区别?
微调和RAG(Retrieval-Augmented Generation)在多个维度上存在显著的区别。以下是它们之间的主要差异: 1. **知识维度**: - RAG对知识的更新时间和经济成本更低。它不需要训练,只需要更新数据库即可。 - RAG对知识的掌控…...
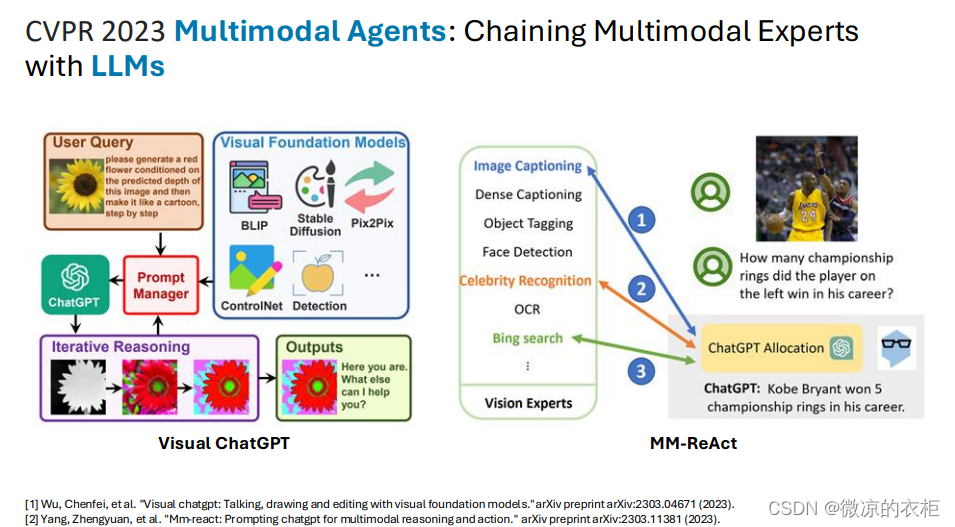
CVPR讲座总结(二)-探索图像生成基础模型的最新进展探索多模态代理的最新进展:从视频理解到可操作代理
引言 在CVPR24上的教程中,微软高级研究员Linjie Li为我们带来了多模态代理的深入探索。这些代理通过整合多模态专家和大语言模型(LLM)来增强感知、理解和生成能力。本文总结了Linjie Li的讲座内容,重点介绍了多模态记忆、可操作代…...

为什么要禁用透明大页面
在安装CDH(Clouderas Distribution Including Apache Hadoop)环境时,禁用透明大页面(Transparent HugePages,THP)是一个推荐的系统优化步骤。以下是禁用透明大页面的一些原因: 1. **性能影响**…...
Element 页面滚动表头置顶
在开发后台管理系统时,表格是最常用的一个组件,为了看数据方便,时常需要固定表头。 如果页面基本只有一个表格区域,我们可以根据屏幕的高度动态的计算出一个值,给表格设定一个固定高度,这样表头就可以固定…...
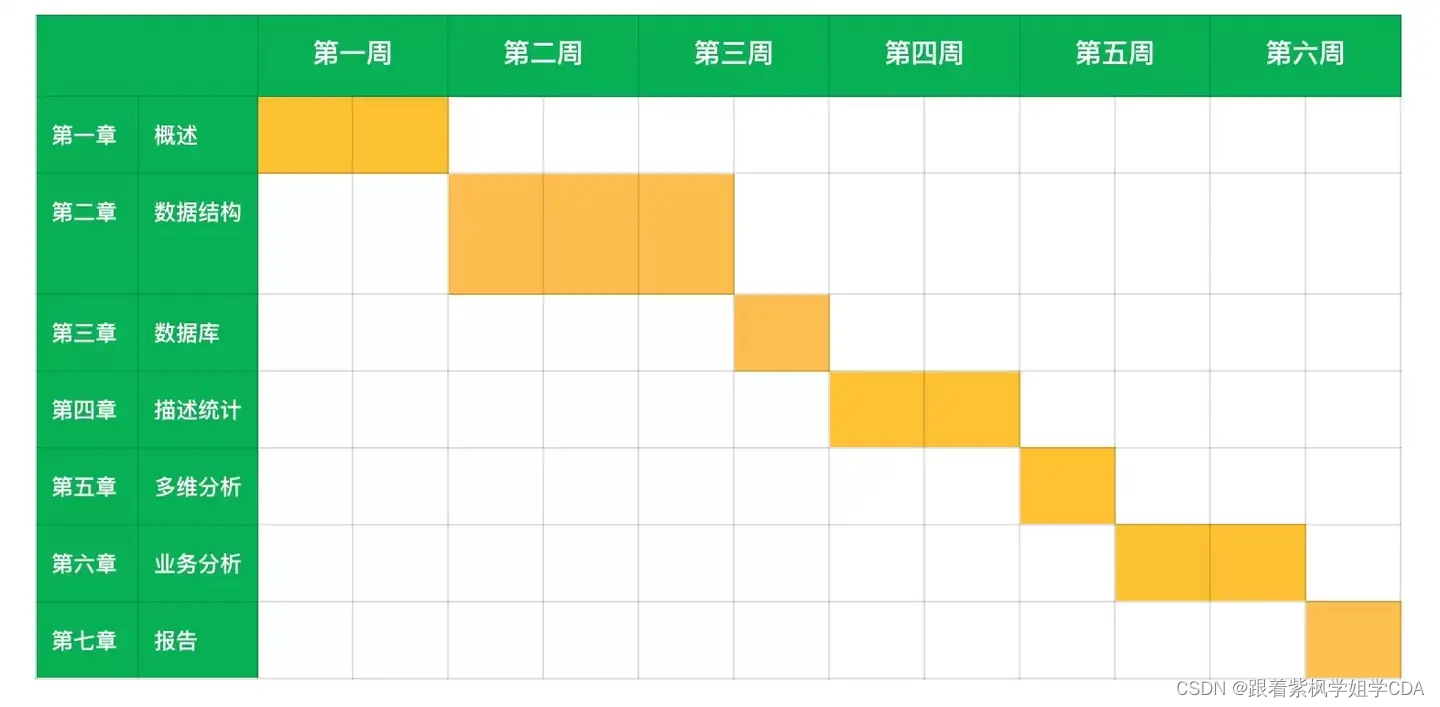
对于CDA一级考试该咋准备??!
一、了解考试内容和结构 CDA一级考试主要涉及的内容包括:数据分析概述与职业操守、数据结构、数据库基础与数据模型、数据可视化分析与报表制作、Power BI应用、业务数据分析与报告编写等。 CDA Level Ⅰ 认证考试大纲:https://edu.cda.cn/group/4/thread/174335 …...

如何使用PHP和Selenium快速构建自己的网络爬虫系统
近年来,随着互联网的普及,网络爬虫逐渐成为了信息采集的主要手段之一,然而,常规的爬虫技术不稳定、难以维护,市面上的纯web网页爬虫也只能在静态页面上进行操作。而php结合selenium可达到动态爬虫的效果,具…...
intellij idea安装R包ggplot2报错问题求解
1、intellij idea安装R包ggplot2问题 在我上次解决图形显示问题后,发现安装ggplot2包时出现了问题,这在之前高版本中并没有出现问题, install.packages(ggplot2) ERROR: lazy loading failed for package lifecycle * removing C:/Users/V…...

【C++】初识C++(一)
一.什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度 的抽象和建模时,C语言则不合适。为了解决软件危机, 20世纪80年代, 计算机界提出了OOP(object o…...
【智能算法】目标检测算法
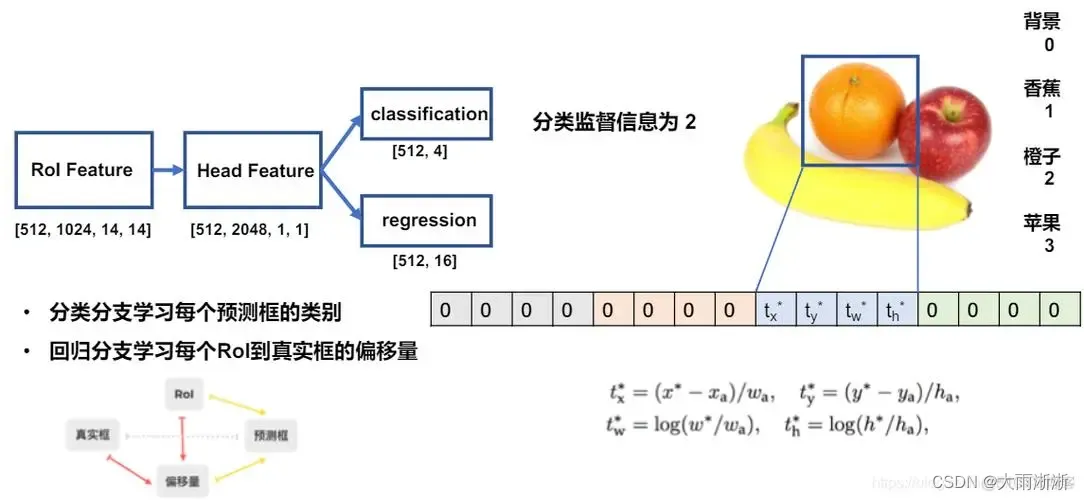
目录 一、目标检测算法分类 二、 常见目标检测算法及matlab代码实现 2.1 R-CNN 2.1.1 定义 2.1.2 matlab代码实现 2.2 Fast R-CNN 2.2.1 定义 2.2.2 matlab代码实现 2.3 Faster R-CNN 2.3.1 定义 2.3.2 matlab代码实现 2.4 YOLO 2.4.1 定义 2.4.2 matlab代码实现…...

python 中 json.load json.loadd json.dump json.dumps 详解
在Python中,json 模块提供了用于处理JSON数据的函数。json.load(), json.loads(), json.dump(), 和 json.dumps() 是这个模块中用于序列化和反序列化JSON数据的主要函数。下面是它们之间的区别详解: json.load() 作用:从一个文件对象&#x…...

【UE 网络】专用服务器和多个客户端加入游戏会话的过程,以及GameMode、PlayerController、Pawn的创建流程
目录 0 引言1 多人游戏会话1.1 Why?为什么要有这个1.2 How?怎么使用? 2 加入游戏会话的流程总结 🙋♂️ 作者:海码007📜 专栏:UE虚幻引擎专栏💥 标题:【UE 网络】在网络…...
区别及操作笔记)
磁盘分区工具(fdisk 和 parted)区别及操作笔记
fdisk 和 parted 都是 Linux 系统中用于磁盘分区的工具。 两者主要区别: 支持的分区表类型: fdisk 主要支持 MBR分区表,MBR分区表支持的硬盘单个分区最大容量为2TB,最多可以有4个主分区。parted 支持 MBR分区表 和 GPT分区表&…...
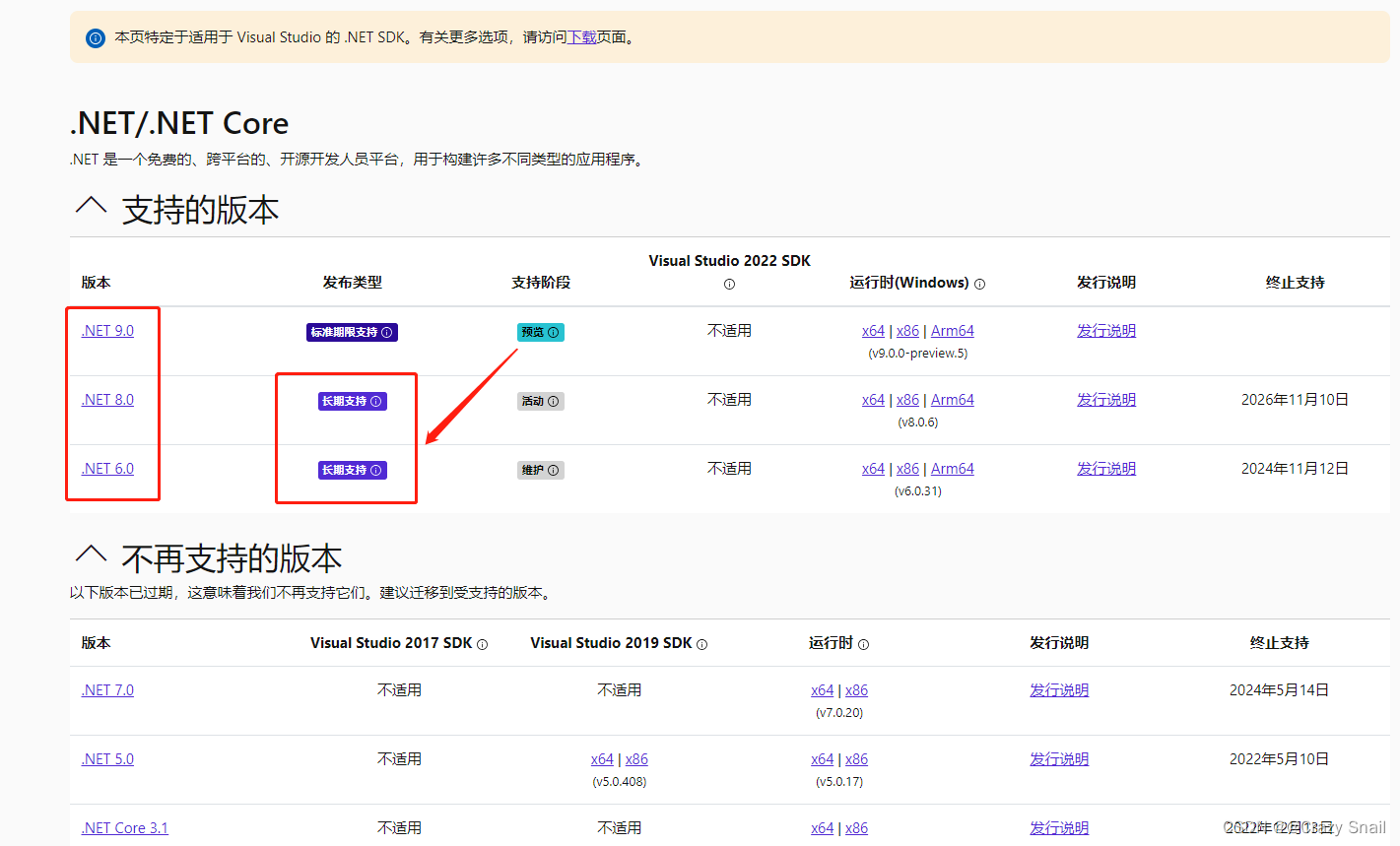
VisualStudio2019受支持的.NET Core
1.VS Studio2019受支持的.NET Core? 适用于 Visual Studio 的 .NET SDK 下载 (microsoft.com) Visual Studio 2019 默认并不直接支持 .NET 6 及以上版本。要使用 .NET 6 或更高版本,你需要在 Visual Studio 2019 中采取额外步骤,比如安装相应…...

Java——IO流(二)-(1/7):字符流-FileReader、FileWriter、字符输出流的注意事项(构造器及常用方法、小结)
目录 文件字符输入流-读字符数据进来 介绍 构造器及常用方法 实例演示 文件字符输出流-写字符数据出去 介绍、构造器及常用方法 实例演示 字符输出流使用时的注意事项 小结 文件字符输入流-读字符数据进来 介绍 FileReader(文件字符输入流) 作…...

Spring循环依赖问题——从源码画流程图
文章目录 关键代码相关知识为什么要使用二级缓存为什么要使用三级缓存只使用两个缓存的问题不能解决构造器循环依赖为什么多例bean不能解决循环依赖问题初始化后代理对象赋值给原始对象解决循环依赖SpringBoot开启循环依赖 循环依赖 在线流程图 关键代码 从缓存中查询getSingl…...
)
Android SurfaceFlinger——动画播放准备(十五)
BootAnimation 本质上是一个线程,执行 run 之后,会先执行 readyToRun,接着执行 treadLoop 方法。 一、线程启动 1、BootAnimation 源码位置:/frameworks/base/cmds/bootanimation/BootAnimation.cpp readyToRun status_t BootAnimation::readyToRun() {// 添加默认资源…...

Zynq7000系列FPGA中的DMA控制器简介(二)
AXI互连上的DMA传输 所有DMA事务都使用AXI接口在PL中的片上存储器、DDR存储器和从外设之间传递数据。PL中的从设备通过DMAC的外部请求接口与DMAC通信,以控制数据流。这意味着从设备可以请求DMA交易,以便将数据从源地址传输到目标地址。 虽然DMAC在技术…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
