算法金 | 欧氏距离算法、余弦相似度、汉明、曼哈顿、切比雪夫、闵可夫斯基、雅卡尔指数、半正矢、Sørensen-Dice

大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
抱个拳,送个礼
在算法模型构建中,我们经常需要计算样本之间的相似度,通常的做法是计算样本之间的距离。 今天,一键拿下九种距离算法。走你~
一、欧氏距离 (Euclidean Distance)
定义与公式
欧氏距离是两个点在 n 维空间中直线距离的度量。它是最常见的距离度量方法之一,用于计算两个向量之间的距离。欧氏距离的公式如下:

应用场景
欧氏距离广泛应用于许多领域,如机器学习、统计学、模式识别和数据挖掘。常见的应用场景包括:
- 分类算法:如 k 近邻 (k-Nearest Neighbors, KNN) 算法,通过计算新样本与训练样本之间的欧氏距离来进行分类
- 聚类分析:如 k 均值 (k-Means) 聚类算法,通过计算样本与聚类中心之间的欧氏距离来确定样本所属的簇
- 图像处理:用于度量图像之间的相似度,如图像检索和图像匹配
优缺点分析
优点:
- 计算简单:欧氏距离的计算公式简单易懂,且计算量较小,适用于大多数应用场景
- 直观性强:欧氏距离直接反映了两个点之间的几何距离,具有很强的直观性
缺点:
- 对尺度敏感:不同维度的数值尺度差异会影响距离的计算结果,需要对数据进行标准化或归一化处理
- 对异常值敏感:欧氏距离对数据中的异常值非常敏感,异常值可能会显著影响计算结果

欧氏距离(Euclidean Distance)
二、余弦相似度 (Cosine Similarity)
定义与公式
余弦相似度是一种衡量两个向量夹角余弦值的度量,常用于评估两个向量的相似度。公式如下:

应用场景
余弦相似度在许多领域有广泛应用,特别是文本和信息检索领域:
- 文本相似度计算:在自然语言处理 (NLP) 中,余弦相似度用于计算两个文本或文档之间的相似度,通过比较它们的词频向量
- 推荐系统:如用户-物品推荐系统,通过计算用户之间或物品之间的相似度来进行推荐
- 图像相似度计算:在计算机视觉中,用于比较图像特征向量的相似度
优缺点分析
优点:
- 不受向量长度影响:余弦相似度仅关注向量的方向,而不受向量的长度影响,适用于不同规模的数据
- 计算简单:公式简单,计算效率高,适合大规模数据处理
缺点:
- 无法反映数值大小的差异:余弦相似度仅考虑向量的方向,不考虑数值的大小,可能会忽略重要的数值信息
- 对稀疏向量效果较差:对于稀疏向量(如文本数据中的词频向量),计算结果可能不准确,需要结合其他方法使用
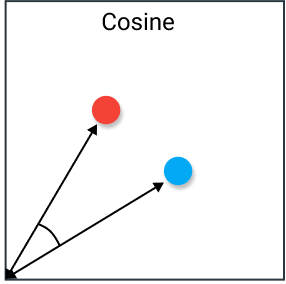
余弦相似度(Cosine Similarity)
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3

更多内容,见免费知识星球
三、汉明距离 (Hamming Distance)
定义与公式
汉明距离用于衡量两个等长字符串之间的不同字符个数。公式如下:
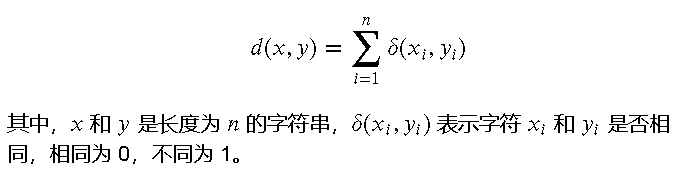
应用场景
汉明距离主要用于以下场景:
- 错误检测和纠正:在通信和存储系统中,用于检测和纠正数据传输和存储中的错误,如汉明码
- 基因序列分析:在生物信息学中,用于比较 DNA 和 RNA 序列之间的差异
- 密码学:在密码分析中,用于比较不同密文之间的差异
优缺点分析
优点:
- 计算简单:汉明距离的计算过程非常简单,适合大规模数据处理
- 适用于离散数据:汉明距离特别适用于比较离散数据,如字符串和二进制数据
缺点:
- 仅适用于等长字符串:汉明距离只能比较长度相同的字符串,对于长度不同的字符串无法计算
- 不考虑字符位置的重要性:汉明距离只关注字符是否相同,不考虑字符在字符串中的位置重要性

汉明距离(Hamming Distance)
四、曼哈顿距离 (Manhattan Distance)
定义与公式
曼哈顿距离,又称为城市街区距离,是指两个点在 n 维空间中各个坐标轴上的距离之和。公式如下:

应用场景
曼哈顿距离在以下领域有广泛应用:
- 数据挖掘和机器学习:如在 k 近邻 (KNN) 算法中,用于计算样本之间的距离
- 图像处理:用于图像像素之间的距离计算,如图像匹配和分割
- 机器人路径规划:在路径规划中,用于计算机器人在网格地图中的移动距离
优缺点分析
优点:
- 计算简单:曼哈顿距离的计算公式简单,计算量较小,适用于大多数应用场景
- 适用于高维数据:在高维空间中,曼哈顿距离比欧氏距离更稳定,不易受到个别维度异常值的影响
缺点:
- 不适用于所有场景:曼哈顿距离在某些场景中可能不如欧氏距离直观,如需要考虑斜向移动的场景
- 对尺度敏感:不同维度的数值尺度差异会影响距离的计算结果,需要对数据进行标准化或归一化处理

曼哈顿距离(Manhattan Distance)
抱个拳,送个礼
点击 ↑ 领取
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3
免费知识星球,欢迎加入交流
五、切比雪夫距离 (Chebyshev Distance)
定义与公式
切比雪夫距离,又称为棋盘距离,是指两个点在 n 维空间中各个坐标轴上的最大距离。公式如下:
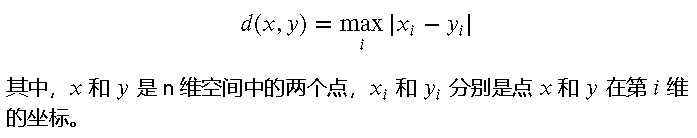
应用场景
切比雪夫距离在以下领域有应用:
- 棋盘游戏:如国际象棋中,王每次可以沿任意方向移动一个格子,切比雪夫距离用于计算王移动的步数
- 仓储和物流:在仓储管理中,用于计算物品在网格仓库中的最远距离
优缺点分析
优点:
- 计算简单:切比雪夫距离的计算公式简单,计算量小,适用于需要快速计算距离的场景
- 直观性强:对于某些特定场景,如棋盘游戏,切比雪夫距离具有很强的直观性
缺点:
- 应用范围有限:切比雪夫距离主要适用于特定场景,不适合所有类型的数据分析
- 对异常值敏感:切比雪夫距离对数据中的异常值非常敏感,异常值可能会显著影响计算结果

切比雪夫距离(Chebyshev Distance)
六、闵可夫斯基距离 (Minkowski Distance)
定义与公式
闵可夫斯基距离是欧氏距离和曼哈顿距离的广义形式,通过调整参数 𝑝𝑝,可以得到不同的距离度量。公式如下:

应用场景
闵可夫斯基距离广泛应用于数据分析和机器学习中:
- 分类算法:如 k 近邻 (KNN) 算法中,通过调整 𝑝𝑝 值来选择适合的距离度量
- 聚类分析:如 k 均值 (k-Means) 聚类算法中,通过调整 𝑝𝑝 值来确定样本与聚类中心之间的距离
优缺点分析
优点:
- 灵活性高:通过调整参数 𝑝,可以得到不同的距离度量,适应不同的应用场景
- 计算公式统一:无论是曼哈顿距离还是欧氏距离,均可以通过统一的闵可夫斯基距离公式来计算
缺点:
- 参数选择困难:在实际应用中,选择合适的 𝑝𝑝 值可能比较困难,需要根据具体问题进行调整
- 对异常值敏感:闵可夫斯基距离对数据中的异常值较为敏感,可能会影响计算结果

闵可夫斯基距离 (Minkowski Distance)
抱个拳,送个礼
点击 ↑ 领取
七、雅卡尔指数 (Jaccard Index)
定义与公式
雅卡尔指数用于衡量两个集合的相似度,其值为两个集合交集的大小除以并集的大小。公式如下:

应用场景
雅卡尔指数在以下领域有广泛应用:
- 信息检索:用于评估搜索结果与查询的相关性
- 图像处理:用于比较图像分割结果与真实分割的相似度
- 生态学:用于比较不同物种群落之间的相似度
优缺点分析
优点:
- 适用于集合数据:雅卡尔指数特别适用于比较离散的集合数据
- 计算简单:雅卡尔指数的计算过程简单,适用于大规模数据处理
缺点:
- 对稀疏数据效果较差:对于稀疏数据(如文本数据),雅卡尔指数可能不准确,需要结合其他方法使用
- 无法处理权重信息:雅卡尔指数仅考虑集合中元素的存在与否,不考虑元素的权重信息

雅卡尔指数(Jaccard Index)
八、半正矢距离 (Haversine Distance)
定义与公式
半正矢距离用于计算地球表面上两点之间的最短距离,考虑到地球的球形特性。公式如下:

应用场景
半正矢距离主要用于以下场景:
- 地理信息系统 (GIS):用于计算地球表面两点之间的最短距离
- 导航系统:用于GPS导航系统中,计算起点和终点之间的距离
- 航空和海洋运输:用于计算航线和航程
优缺点分析
优点:
- 考虑地球曲率:半正矢距离考虑到地球的球形特性,计算结果更准确
- 适用于长距离计算:对于长距离的两点间距离计算,半正矢距离比直线距离更准确
缺点:
- 计算复杂:半正矢距离的计算公式较复杂,计算量较大,不适合实时计算
- 对短距离不敏感:对于短距离的两点间距离计算,半正矢距离与直线距离差异不大

半正矢距离 (Haversine Distance)
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3

免费知识星球,欢迎加入,一起交流切磋
九、Sørensen-Dice 系数
(Sørensen-Dice Coefficient)
定义与公式
Sørensen-Dice 系数用于衡量两个集合的相似度,其值为两个集合交集的大小的两倍除以两个集合大小的总和。公式如下:

应用场景
Sørensen-Dice 系数在以下领域有广泛应用:
- 信息检索:用于评估搜索结果与查询的相关性
- 图像处理:用于比较图像分割结果与真实分割的相似度
- 生态学:用于比较不同物种群落之间的相似度
优缺点分析
优点:
- 适用于集合数据:Sørensen-Dice 系数特别适用于比较离散的集合数据
- 计算简单:Sørensen-Dice 系数的计算过程简单,适用于大规模数据处理
缺点:
- 对稀疏数据效果较差:对于稀疏数据(如文本数据),Sørensen-Dice 系数可能不准确,需要结合其他方法使用
- 无法处理权重信息:Sørensen-Dice 系数仅考虑集合中元素的存在与否,不考虑元素的权重信息
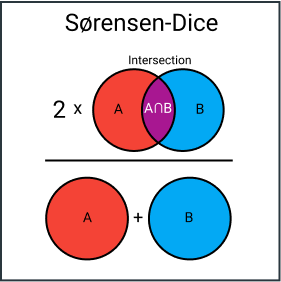
Sørensen-Dice 系数 (Sørensen-Dice Coefficient)
[ 抱个拳,总个结 ]
各种距离和相似度的对比分析
数学性质对比
- 欧氏距离:度量空间中两点之间的直线距离,具有平移不变性和对称性
- 余弦相似度:度量两个向量之间夹角的余弦值,仅考虑向量的方向,不考虑向量的大小
- 汉明距离:度量两个等长字符串之间不同字符的个数,适用于离散数据
- 曼哈顿距离:度量空间中两点在各坐标轴上的距离之和,适用于高维数据
- 切比雪夫距离:度量两个点在各坐标轴上的最大距离,适用于棋盘游戏等特定场景
- 闵可夫斯基距离:欧氏距离和曼哈顿距离的广义形式,通过调整参数 𝑝𝑝 可得到不同的距离度量
- 雅卡尔指数:度量两个集合的相似度,计算两个集合交集与并集的比值
- 半正矢距离:计算地球表面两点间的最短距离,考虑地球的球形特性
- Sørensen-Dice 系数:度量两个集合的相似度,计算两个集合交集大小的两倍与两个集合大小总和的比值
计算复杂度对比
- 欧氏距离:𝑂(𝑛),计算简单,适用于大多数应用场景
- 余弦相似度:𝑂(𝑛),计算简单,适合大规模数据处理
- 汉明距离:𝑂(𝑛),计算简单,适合离散数据
- 曼哈顿距离:𝑂(𝑛),计算简单,适用于高维数据
- 切比雪夫距离:𝑂(𝑛),计算简单,适用于特定场景
- 闵可夫斯基距离:𝑂(𝑛),通过调整参数 𝑝𝑝,适应不同的应用场景
- 雅卡尔指数:𝑂(𝑛),计算简单,适用于集合数据
- 半正矢距离:𝑂(1),公式复杂,适合地理信息系统等场景
- Sørensen-Dice 系数:𝑂(𝑛),计算简单,适用于集合数据
适用场景对比
- 欧氏距离:适用于空间距离计算、分类算法(如 KNN)、聚类分析(如 K-Means)
- 余弦相似度:适用于文本相似度计算、推荐系统、图像相似度计算
- 汉明距离:适用于错误检测和纠正、基因序列分析、密码学
- 曼哈顿距离:适用于数据挖掘和机器学习、图像处理、机器人路径规划
- 切比雪夫距离:适用于棋盘游戏、仓储和物流
- 闵可夫斯基距离:适用于分类算法、聚类分析
- 雅卡尔指数:适用于信息检索、图像处理、生态学
- 半正矢距离:适用于地理信息系统、导航系统、航空和海洋运输
- Sørensen-Dice 系数:适用于信息检索、图像处理、生态学
核心要点回顾
- 欧氏距离:计算空间中两点间的直线距离,简单易懂
- 余弦相似度:计算两个向量间夹角的余弦值,适合文本和向量数据
- 汉明距离:计算两个等长字符串间不同字符的个数,适合离散数据
- 曼哈顿距离:计算空间中两点在各坐标轴上的距离之和,适合高维数据
- 切比雪夫距离:计算两点间各坐标轴上的最大距离,适用于特定场景
- 闵可夫斯基距离:欧氏距离和曼哈顿距离的广义形式,通过参数调整适应不同场景
- 雅卡尔指数:计算两个集合的相似度,适合集合数据
- 半正矢距离:计算地球表面两点间的最短距离,考虑地球曲率
- Sørensen-Dice 系数:计算两个集合的相似度,适合集合数据
- 科研为国分忧,创新与民造福 -

日更时间紧任务急,难免有疏漏之处,还请大侠海涵 内容仅供学习交流之用,部分素材来自网络,侵联删
[ 算法金,碎碎念 ]
这个神反馈,
有点意思
hhh~
全网同名,日更万日,让更多人享受智能乐趣
如果觉得内容有价值,烦请大侠多多 分享、在看、点赞,助力算法金又猛又持久、很黄很 BL 的日更下去;
同时邀请大侠 关注、星标 算法金,围观日更万日,助你功力大增、笑傲江湖
相关文章:

算法金 | 欧氏距离算法、余弦相似度、汉明、曼哈顿、切比雪夫、闵可夫斯基、雅卡尔指数、半正矢、Sørensen-Dice
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 在算法模型构建中,我们经常需要计算样本之间的相似度,通常的做法是计算样本之间的距…...

项目实战--Spring Boot大数据量报表Excel优化
一、项目场景 项目中要实现交易报表,处理大规模数据导出时,出现单个Excel文件过大导致性能下降的问题,需求是导出大概四千万条数据到Excel文件,不影响正式环境的其他查询。 二、方案 1.使用读写分离,查询操作由从库…...

C#编程技术指南:从入门到精通的全面教程
无论你是编程新手,还是想要深化.NET技能的开发者,本文都将为你提供一条清晰的学习路径,从C#基础到高级特性,每一站都配有详尽解析和实用示例,旨在帮助你建立坚实的知识体系,并激发你对C#及.NET生态的热情。…...

Redis+定式任务实现简易版消息队列
Redis是一个开源的内存中数据结构存储系统,通常被用作数据库、缓存和消息中间件。 Redis主要将数据存储在内存中,因此读写速度非常快。 支持不同的持久化方式,可以将内存中的数据定期写入磁盘,保证数据持久性。 redis本身就有自己…...

学习在 C# 中使用 Lambda 运算符
在 C# 中,lambda 运算符 > 同时用于 lambda 表达式和表达式体成员。 1. Lambda 表达式 Lambda 表达式是一种简洁的表示匿名方法(没有名称的方法)的方法。它使用 lambda 运算符 >,可以读作“转到”。运算符的左侧指定输入参…...
)
数据结构和算法,单链表的实现(kotlin版)
文章目录 数据结构和算法,单链表的实现(kotlin版)b站视频链接1.定义接口,我们需要实现的方法2.定义节点,表示每个链表节点。3.push(e: E),链表尾部新增一个节点4.size(): Int,返回链表的长度5.getValue(index: Int): E…...

Jdk17是否有可能代替 Jdk8
JDK发展历史和开源 2006年SUN公司开源JDK,成立OpenJDK组织。2009年Oracle收购SUN,加快JDK发布周期。Oracle JDK与OpenJDK功能基本一致,但Oracle JDK提供更长时间的更新支持。 JDK版本特性 JDK11是长期支持版本(LTS)…...

oca和 ocp有什么区别
OCA(Oracle Certified Associate)和OCP(Oracle Certified Professional)在Oracle的认证体系中是两种不同级别的认证,它们之间存在明显的区别。以下是对两者区别的详细解释: 认证级别: OCA&…...

煤矿安全大模型:微调internlm2模型实现针对煤矿事故和煤矿安全知识的智能问答
煤矿安全大模型————矿途智护者 使用煤矿历史事故案例,事故处理报告、安全规程规章制度、技术文档、煤矿从业人员入职考试题库等数据,微调internlm2模型实现针对煤矿事故和煤矿安全知识的智能问答。 本项目简介: 近年来,国家对煤矿安全生产的重视程度不断提升。为了确…...

C++中的C++中的虚析构函数的作用和重要性
在C中,虚析构函数(virtual destructor)的作用和重要性主要体现在多态和继承的上下文中。了解这一点之前,我们先简要回顾一下多态和继承的基本概念。 继承与多态 继承:允许我们定义一个基类(也称为父类或超…...

机器学习 - 文本特征处理之 TF 和 IDF
TF(Term Frequency,词频)和IDF(Inverse Document Frequency,逆文档频率)是文本处理和信息检索中的两个重要概念,常用于计算一个词在文档中的重要性。下面是详细解释: TF(…...
因为自己淋过雨所以想给嵌入式撑把伞
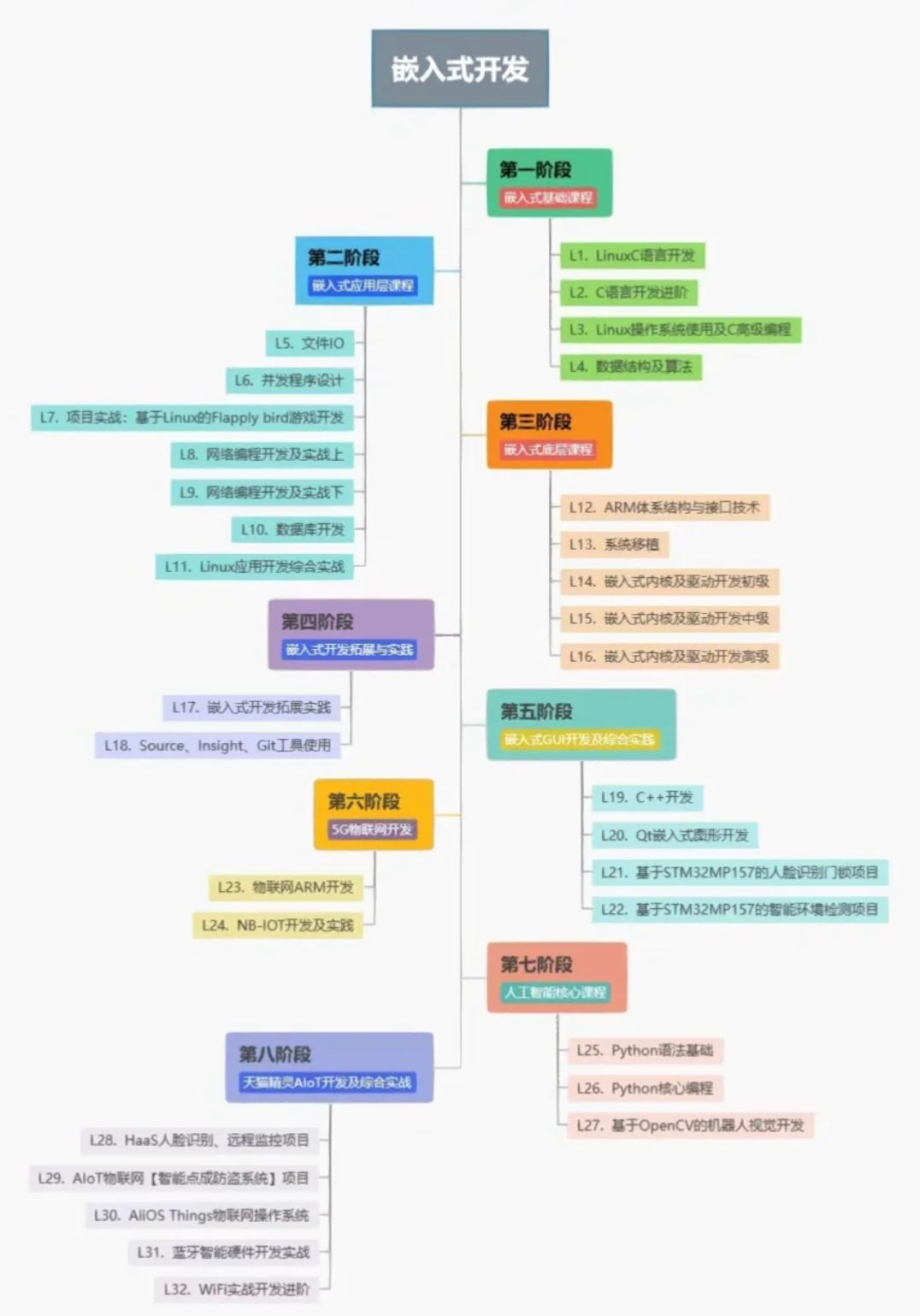
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「嵌入式的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!新手学嵌入式,…...

《C++20设计模式》中单例模式
文章目录 一、前言二、饿汉式1、实现 三、懒汉式1、实现 四、最后 一、前言 单例模式定义: 单例模式(Singleton Pattern)是一种创建型设计模式,其主要目的是确保一个类只有一个实例,并提供全局访问点来访问这个实例。…...
前端技术(说明篇)
Introduction ##编写内容:1.前端概念梳理 2.前端技术种类 3.前端学习方式 ##编写人:贾雯爽 ##最后更新时间:2024/07/01 Overview 最近在广州粤嵌进行实习,项目名称是”基于Node实现多人聊天室“,主要内容是对前端界…...
带电池监控功能的恒流直流负载组
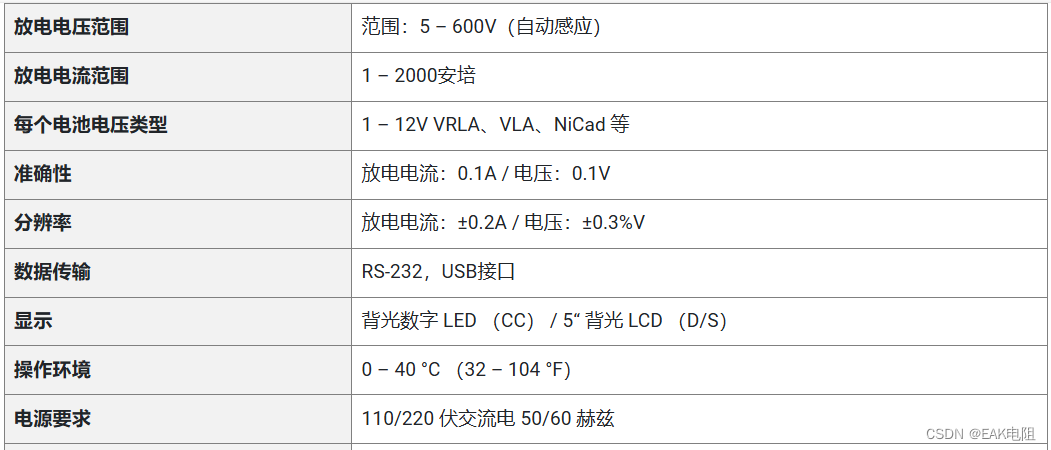
EAK的交流和直流工业电池负载组测试仪对于测试和验证关键电力系统的能力至关重要,旨在实现最佳精度。作为一家客户至上的公司,我们继续尽我们所能应对供应链挑战,以提供出色的交货时间,大约是行业其他公司的一半。 交流负载组 我…...

关于Disruptor监听策略
Disruptor框架提供了多种等待策略,每种策略都有其适用的场景和特点。以下是这些策略的详细介绍及其适用场景: 1. BlockingWaitStrategy 特点: 使用锁和条件变量进行线程间通信,线程在等待时会进入阻塞状态,释放CPU资…...
)
大数据面试题之HBase(3)
HBase的预分区 HBase的热点问题 HBase的memstore冲刷条件 HBase的MVCC HBase的大合并与小合并,大合并是如何做的?为什么要大合并 既然HBase底层数据是存储在HDFS上,为什么不直接使用HDFS,而还要用HBase HBase和Phoenix的区别 HBase支…...

c#中赋值、浅拷贝和深拷贝
在 C# 编程中,深拷贝(Deep Copy)和浅拷贝(Shallow Copy)是用于复制对象的两种不同方式,它们在处理对象时有着重要的区别和适用场景。 浅拷贝(Shallow Copy) 浅拷贝是指创建一个新对…...

旧版st7789屏幕模块 没有CS引脚的天坑 已解决!!!
今天解决了天坑一个,大家可能有的人买的是st7789屏幕模块,240x240,1.3寸的 他标注的是老版,没有CS引脚,小崽子长这样: 这熊孩子用很多通用的驱动不吃,死活不显示,网上猛搜ÿ…...

激光粒度分析仪校准步骤详解:提升测量精度的秘诀
在材料科学、环境监测、医药研发等众多领域,激光粒度分析仪以其高精度、高效率的测量性能,成为了不可或缺的测试工具。然而,为了保持其测量结果的准确性和可靠性,定期校准是不可或缺的步骤。 接下来,佰德将为您详细介…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
