【C++】双线性差值算法实现RGB图像缩放
双线性差值算法
双线性插值(Bilinear Interpolation)并不是“双线性差值”,它是一种在二维平面上估计未知数据点的方法,通常用于图像处理中的图像缩放。
双线性插值的基本思想是:对于一个未知的数据点,我们找到其最近的4个已知数据点,然后根据这4个已知数据点的值以及它们与未知数据点的距离,来估计未知数据点的值。
具体到图像处理中,如果我们想要将一个图像从一个尺寸放大或缩小到另一个尺寸,我们可以使用双线性插值来估计新尺寸下每个像素点的颜色值。
以下是双线性插值的数学公式:
设我们要估计的点为P(x,y),其最近的4个已知点为A(x0,y0),B(x1,y0),C(x0,y1),D(x1,y1),则P点的值I_P可以表示为:
I_P = I_A * (x1-x)(y1-y) + I_B * (x-x0)(y1-y) + I_C * (x1-x)(y-y0) + I_D * (x-x0)(y-y0)
其中,I_A,I_B,I_C,I_D分别为A,B,C,D点的值。
在实际应用中,我们通常会使用浮点数来表示x和y,这样可以得到更精确的结果。但是,由于x和y可能是小数,所以我们需要使用floor和ceil函数来找到最近的4个整数坐标点。
C++双线性差值算法RGB图像缩放
/**@func Imresize
* @brief 双线性差值算法缩放RGB图片
* @param[out] pfDst 目的图像地址
* @param[in] nW 目的图像宽度
* @param[in] nH 目的图像高度
* @param[in] pfSrc 源图像地址
* @param[in] nOriW 源图像宽度
* @param[in] nOriH 源图像高度
*/
void Imresize(unsigned char *pfDst, int nH, int nW, unsigned char *pfSrc, int nOriH, int nOriW)
{for (int i = 0; i < nH * nW; i++){int row = i / nW;int col = i % nW;float x = (row + 0.5) * nOriH / nH - 0.5;if (x < 0) x = 0;if (x >= nOriH - 1) x = nOriH - 2;int fx = (int)x;x = x - fx;float x1 = 1.0 - x;float y = (col + 0.5) * nOriW / nW - 0.5;if (y < 0) y = 0;if (y >= nOriW - 1) y = nOriW - 2;int fy = (int)y;y = y - fy;float y1 = 1.0 - y;float val_R = (pfSrc[fx * nOriW * 3 + 3 * fy] * x1 * y1 + pfSrc[(fx + 1) * nOriW * 3 + 3 * fy] * x * y1+ pfSrc[fx * nOriW * 3 + (fy + 1) * 3] * x1 * y + pfSrc[(fx + 1) * nOriW * 3 + (fy + 1) * 3] * x * y);float val_G = (pfSrc[fx * nOriW * 3 + 1 + 3 * fy] * x1 * y1 + pfSrc[(fx + 1) * nOriW * 3 + 1 + 3 * fy] * x * y1+ pfSrc[fx * nOriW * 3 + 1 + (fy + 1) * 3] * x1 * y + pfSrc[(fx + 1) * nOriW * 3 + 1 + (fy + 1) * 3] * x * y);float val_B = (pfSrc[fx * nOriW * 3 + 2 + 3 * fy] * x1 * y1 + pfSrc[(fx + 1) * nOriW * 3 + 2 + 3 * fy] * x * y1+ pfSrc[fx * nOriW * 3 + 2 + (fy + 1) * 3] * x1 * y + pfSrc[(fx + 1) * nOriW * 3 + 2 + (fy + 1) * 3] * x * y);pfDst[i * 3] = unsigned char(val_B);pfDst[i * 3 + 1] = unsigned char(val_G);pfDst[i * 3 + 2] = unsigned char(val_R);}
}
使用OpenCV库实现双线性差值算法RGB图像缩放
#include <opencv2/opencv.hpp>cv::Mat bilinearInterpolation(const cv::Mat& src, int newWidth, int newHeight) {cv::Mat dst(newHeight, newWidth, CV_8UC3);float x_ratio = src.cols / (float)newWidth;float y_ratio = src.rows / (float)newHeight;for(int dst_y = 0; dst_y < newHeight; dst_y++) {for(int dst_x = 0; dst_x < newWidth; dst_x++) {// 计算源图像中的位置float src_x = (dst_x + 0.5f) * x_ratio - 0.5f;float src_y = (dst_y + 0.5f) * y_ratio - 0.5f;// 找到最邻近的四个像素点int x0 = floor(src_x);int y0 = floor(src_y);int x1 = ceil(src_x);int y1 = ceil(src_y);// 确保坐标在图像范围内x0 = std::min(std::max(0, x0), src.cols - 2);y0 = std::min(std::max(0, y0), src.rows - 2);x1 = std::min(std::max(0, x1), src.cols - 2);y1 = std::min(std::max(0, y1), src.rows - 2);// 双线性插值计算float dx = src_x - x0;float dy = src_y - y0;cv::Vec3b top = src.at<cv::Vec3b>(y0, x0) * (1 - dx) + src.at<cv::Vec3b>(y0, x1) * dx;cv::Vec3b bottom = src.at<cv::Vec3b>(y1, x0) * (1 - dx) + src.at<cv::Vec3b>(y1, x1) * dx;dst.at<cv::Vec3b>(dst_y, dst_x) = top * (1 - dy) + bottom * dy;}}return dst;
}使用双线性差值算法需要注意的点
使用双线性插值算法时,需要注意以下几点:
-
边界处理:在计算目标像素对应的源图像坐标时,可能会出现超出边界的情况。例如,如果目标像素对应的位置在源图像的边界之外,那么你就找不到四个邻近的像素。这时,你可能需要做一些特殊的处理,比如将坐标限制在图像的边界内,或者使用边界上的像素值进行插值。
-
精度问题:双线性插值涉及到浮点数运算,可能会有精度损失。此外,如果你的目标图像的尺寸远大于源图像,那么可能会出现“模糊”的效果,这是因为插值算法无法创造出新的信息。
-
颜色空间:如果你处理的是彩色图像,那么你需要对每个颜色通道分别进行插值。在某些情况下,可能需要考虑颜色空间的影响,例如在HSV颜色空间中,色相(H)通道的插值可能需要特殊处理,因为它是一个循环的量。
-
性能问题:双线性插值需要对每个像素进行四次访问和一次乘法操作,这可能会导致性能问题。如果你需要处理大尺寸的图像,或者需要实时处理图像,那么你可能需要考虑使用更高效的算法,或者使用硬件加速。
-
其他插值方法:双线性插值只是众多插值方法中的一种,还有最近邻插值、双三次插值等方法。不同的插值方法有不同的优缺点,你需要根据你的具体需求选择最适合的插值方法。
相关文章:

【C++】双线性差值算法实现RGB图像缩放
双线性差值算法 双线性插值(Bilinear Interpolation)并不是“双线性差值”,它是一种在二维平面上估计未知数据点的方法,通常用于图像处理中的图像缩放。 双线性插值的基本思想是:对于一个未知的数据点,我…...
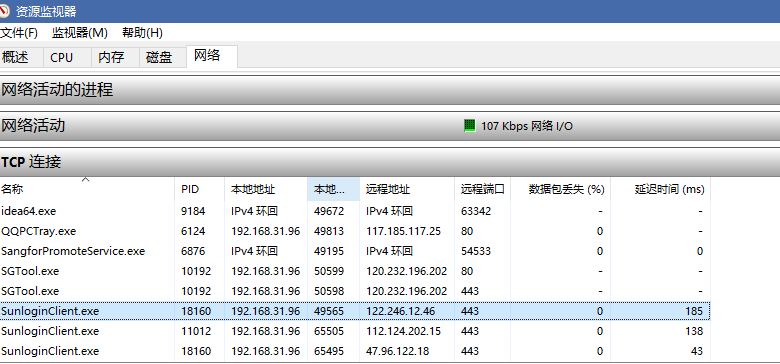
计算机网络知识普及之四元组
在涉及到TCP/UDP等IP类通信协议时,存在四元组概念 这里只是普及使用 先来一些前置知识,什么是IP协议? IP协议全称为互联网协议,处于网络层中,主要作用是标识网络中的设备,每个设备的IP地址是唯一的。 在网…...

深度探讨网络安全:挑战、防御策略与实战案例
目录 编辑 一、引言 二、网络安全的主要挑战 恶意软件与病毒 数据泄露 分布式拒绝服务攻击(DDoS) 内部威胁 三、防御策略与实战案例 恶意软件防护 网络钓鱼防护 数据泄露防护 总结 一、引言 随着信息技术的迅猛发展,网络安全问…...

“穿越时空的机械奇观:记里鼓车的历史与科技探秘“
在人类文明的发展历程中,科技的创新与进步不仅仅推动了社会的进步,也为我们留下了丰富的文化遗产。记里鼓车,作为一种古老的里程计量工具,其历史地位和技术成就在科技史上具有重要的意义。本文将详细介绍记里鼓车的起源、结构原理…...

DevOps CMDB平台整合Jira工单
背景 在DevOps CMDB平台建设的过程中,我们可以很容易的将业务应用所涉及的云资源(WAF、K8S、虚拟机等)、CICD工具链(Jenkins、ArgoCD)、监控、日志等一次性的维护到CMDB平台,但随着时间的推移,…...
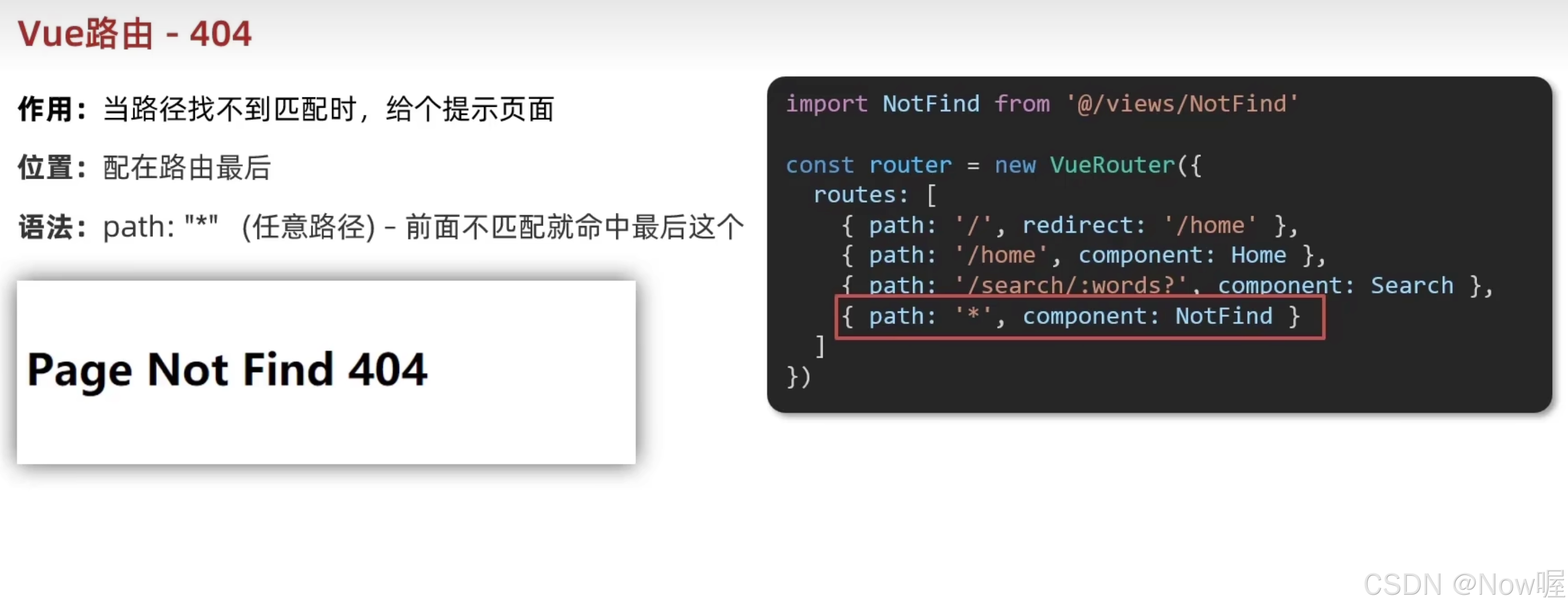
Vue-路由
路由简介 SPA单页面应用。导航区和展示区 单页Web应用整个应用只有一个完整的页面点击页面中的导航连接不会刷新页面,只会做页面的局部更新数据需要通过ajax请求获取 路由:路由就是一组映射关系,服务器接收到请求时,根据请求路…...

【Rust入门教程】安装Rust
文章目录 前言Rust简介Rust的安装更新与卸载rust更新卸载 总结 前言 在当今的编程世界中,Rust语言以其独特的安全性和高效性吸引了大量开发者的关注。Rust是一种系统编程语言,专注于速度、内存安全和并行性。它具有现代化的特性,同时提供了低…...

Character.ai因内容审查流失大量用户、马斯克:Grok-3用了10万块英伟达H100芯片
ChatGPT狂飙160天,世界已经不是之前的样子。 更多资源欢迎关注 1、爆火AI惨遭阉割,1600万美国年轻人失恋?Character.ai被爆资金断裂 美国流行的社交软件Character.ai近期对模型进行大幅度内容审查,导致用户感到失望并开始流失。…...

Spring源码九:BeanFactoryPostProcessor
上一篇Spring源码八:容器扩展一,我们看到ApplicationContext容器通过refresh方法中的prepareBeanFactory方法对BeanFactory扩展的一些功能点,包括对SPEL语句的支持、添加属性编辑器的注册器扩展解决Bean属性只能定义基础变量的问题、以及一些…...

大模型笔记1: Longformer环境配置
论文: https://arxiv.org/abs/2004.05150 目录 库安装 LongformerForQuestionAnswering 库安装 首先保证电脑上配置了git. git环境配置: https://blog.csdn.net/Andone_hsx/article/details/87937329 3.1、找到git安装路径中bin的位置,如:D:\Prog…...
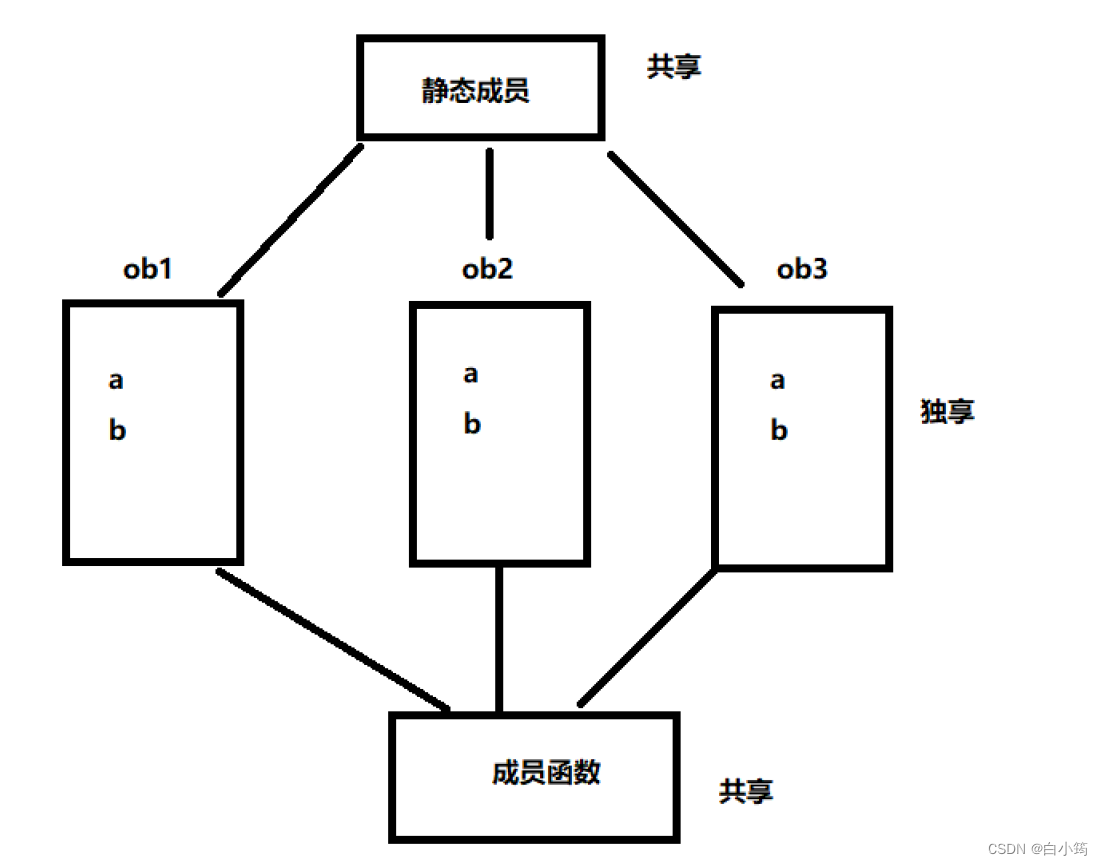
类和对象(提高)
类和对象(提高) 1、定义一个类 关键字class 6 class Data1 7 { 8 //类中 默认为私有 9 private: 10 int a;//不要给类中成员 初始化 11 protected://保护 12 int b; 13 public://公共 14 int c; 15 //在类的内部 不存在权限之分 16 void showData(void)…...

免费最好用的证件照制作软件,一键换底+老照片修复+图片动漫化,吊打付费!
这款软件真的是阿星用过的,最好用的证件照制作软件,没有之一! 我是阿星,今天要给大家安利一款超实用的证件照工具,一键换底,自动排版,免费无广告,让你在家就能轻松搞定证件照&#…...

antfu/ni 在 Windows 下的安装
问题 全局安装 ni 之后,第一次使用会有这个问题 解决 在 powershell 中输入 Remove-Item Alias:ni -Force -ErrorAction Ignore之后再次运行 ni Windows 11 下的 Powershell 环境配置 可以参考 https://github.com/antfu-collective/ni?tabreadme-ov-file#how …...

Linux 生产消费者模型
💓博主CSDN主页:麻辣韭菜💓 ⏩专栏分类:Linux初窥门径⏪ 🚚代码仓库:Linux代码练习🚚 🌹关注我🫵带你学习更多Linux知识 🔝 前言 1. 生产消费者模型 1.1 什么是生产消…...

深入浅出:MongoDB中的背景创建索引
深入浅出:MongoDB中的背景创建索引 想象一下,你正忙于将成千上万的数据塞入你的MongoDB数据库中,你的用户期待着实时的响应速度。此时,你突然想到:“嘿,我应该给这些查询加个索引!” 没错&…...

Spring事务十种失效场景
首先我们要明白什么是事务?它的作用是什么?它在什么场景下在Spring框架下会失效? 事务:本质上是由数据库和程序之间交互的过程中的衍生物,它是一种控制数据的行为规则。有几个特性 1、原子性:执行单元内,要…...

JELR-630HS漏电继电器 30-500mA 导轨安装 约瑟JOSEF
JELR-HS系列 漏电继电器型号: JELR-15HS漏电继电器;JELR-25HS漏电继电器; JELR-32HS漏电继电器;JELR-63HS漏电继电器; JELR-100HS漏电继电器;JELR-120HS漏电继电器; JELR-160HS漏电继电器&a…...

如何实现一个简单的链表或栈结构
实现一个简单的链表或栈结构是面向对象编程中的基础任务。下面我将分别给出链表和栈的简单实现。 链表(单链表)的实现 链表是由一系列节点组成的集合,每个节点都包含数据部分和指向列表中下一个节点的链接(指针或引用࿰…...

抖音外卖服务商入驻流程及费用分别是什么?入驻官方平台的难度大吗?
随着抖音关于新增《【到家外卖】内容服务商开放准入公告》的意见征集通知(以下简称“通知”)的发布,抖音外卖服务商入驻流程及费用逐渐成为众多创业者所关注和热议的话题。不过,就当前的讨论情况来看,这个话题似乎没有…...

“小红书、B站崩了”,背后的阿里云怎么了?
导语:阿里云不能承受之重 文 | 魏强 7月2日,“小红书崩了”、“B站崩了”等话题登上了热搜。 据第一财经、财联社等报道,7月2日,用户在B站App无法使用浏览历史关注等内容,消息界面、更新界面、客服界面均不可用&…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
