数据结构 - C/C++ - 树
- 公开视频 -> 链接点击跳转公开课程
- 博客首页 -> 链接点击跳转博客主页
目录
树的概念
结构特性
树的样式
树的存储
树的遍历
节点增删
二叉搜索树
平衡二叉树
树的概念
-
二叉树是树形结构,是一种非线性结构。
-
非线性结构:在二叉树中,数据项的排列不是简单的线性序列,而是通过节点间的链接构成复杂的层次结构。
-
受限节点数目:每个节点最多有两个子节点,这限定了树的分支宽度。
-
-
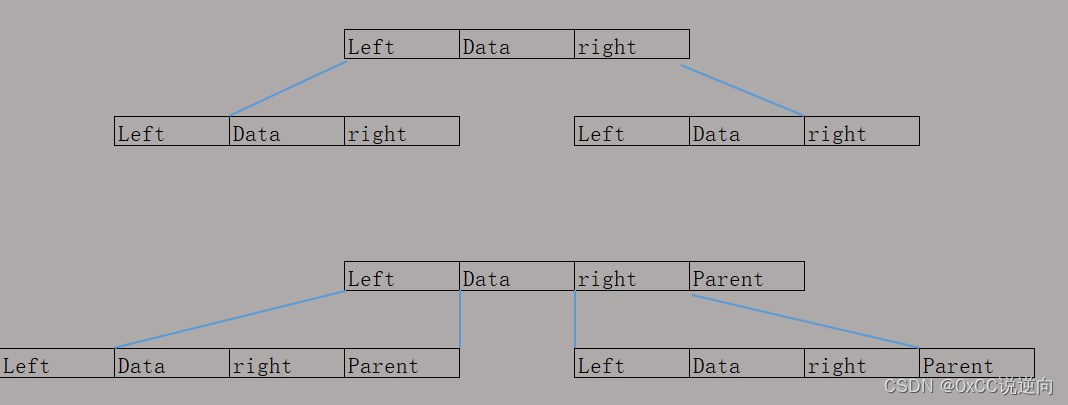
节点(Node)
-
数据域:保存或显示与节点相关联的信息。
-
左子节点指针:指向左侧子节点的链接。
-
右子节点指针:指向右侧子节点的链接。
-
-
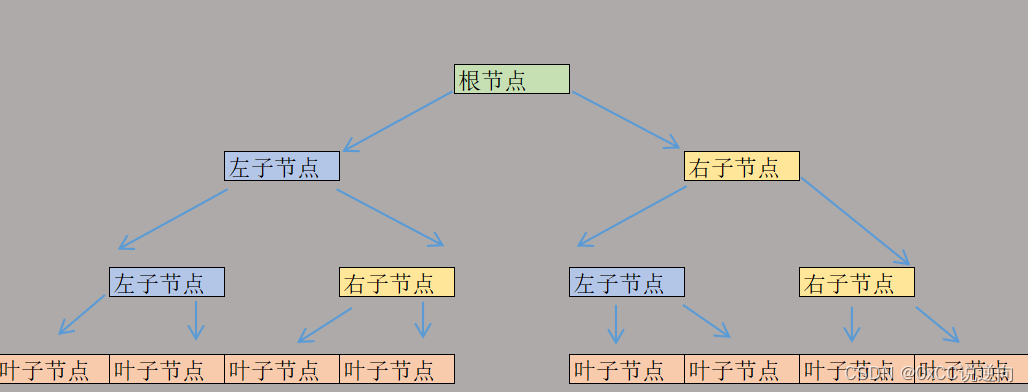
根节点(Root)
-
节点是树结构的最顶端节点,它没有父节点,并且是二叉树结构的起点。
-
-
父节点(Parent)
-
与子节点相关联的上一级节点。
-
-
子节点(Child)
-
父节点指向的左子节点或者右子节点。
-
-
叶子节点(Leaf)
-
叶子节点是指没有任何子节点的节点。在树的结构中,叶子节点总是位于最底层。
-
-
兄弟节点(Brother)
-
在二叉树中,共享同一父节点的两个节点称为兄弟节点。
-
-
节点的度
-
节点分支数。
-
度为0:节点没有子节点,即叶子节点。
-
度为1:节点有一个子节点。
-
度为2:节点有两个子节点。
-
-
结点层度:根节点的层次为1,以此递增。
-
树的深度:树种节点层次的最大值。
结构特性
-
二叉树中第I层中最多存在2^(I - 1)的节点数量。
-
二叉树中深度为I时最多存在2^I - 1的节点总数。
树的样式
-
二叉树
-
-
完美二叉树
-
完美二叉树中,除了叶子节点外其余所有节点的度都有2。
-
完美二叉树中,深度为I时节点数量为2^I - 1。
-
-
树的存储
-
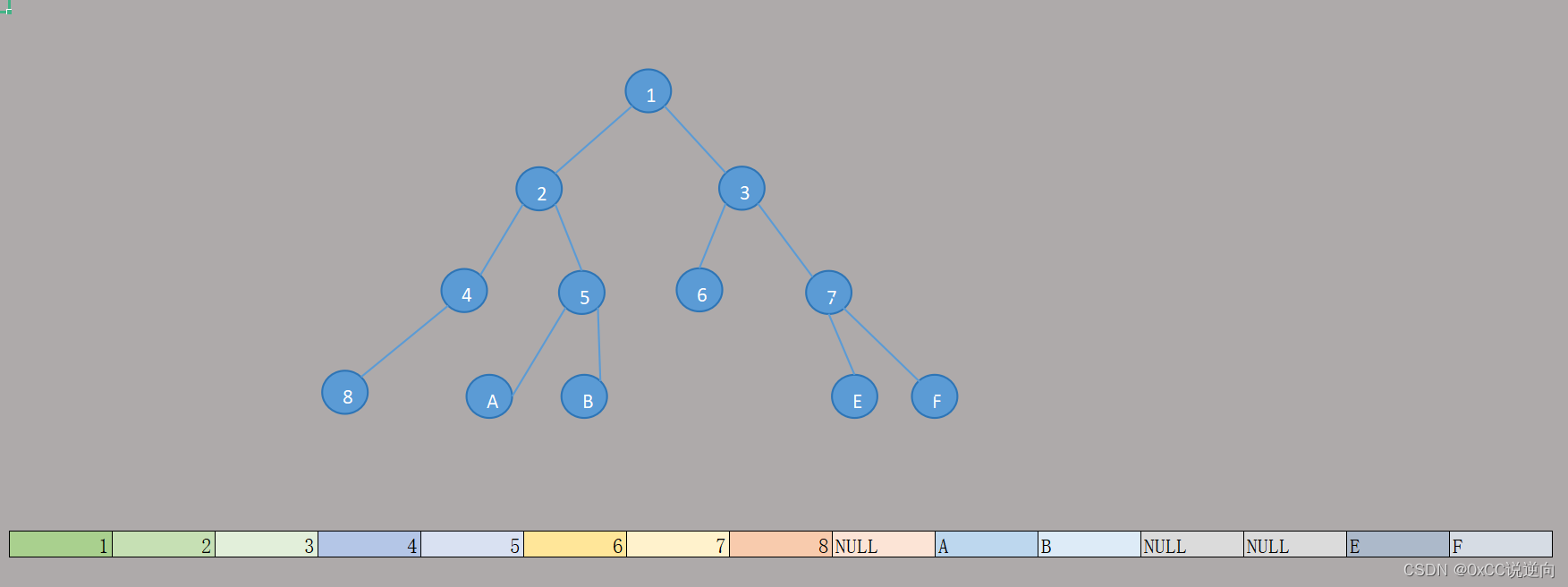
顺序存储
-
基于数组 - 内存中使用连续的内存空间
-
假设根节点编号为x
-
左子节点编号为2 * x
-
右子节点编号为2 * x + 1
-
-
-
-
链式存储
-
基于链表 - ListNode
-
-
树的遍历
-
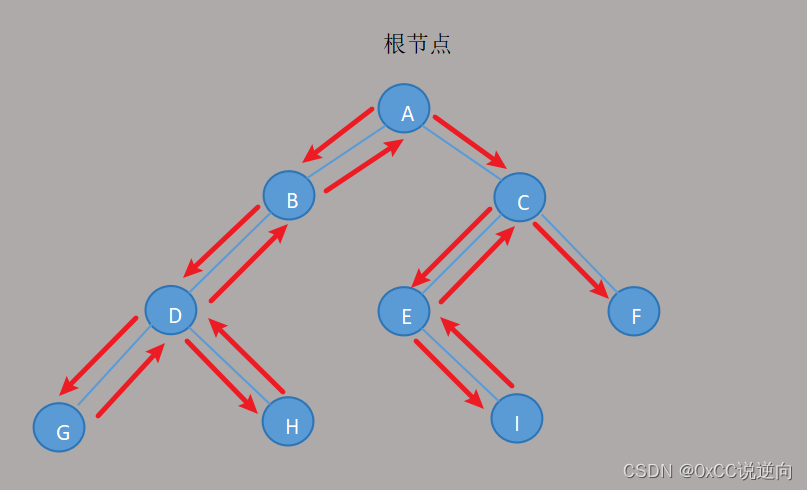
先序遍历 DLR 根节点 左子树 右子树
-
-
中序遍历 LDR 左子树 根节点 右子树
-
后序遍历 LRD 左子树 右子树 根节点
-

-
示例代码
#include <iostream>class TreeNode { public:char ch;TreeNode* Left;TreeNode* Righ;TreeNode(char value) : ch(value), Left(nullptr), Righ(nullptr) {} };void PreorderTraverse(TreeNode* T) {if (T == NULL) return;printf("%c ", T->ch);PreorderTraverse(T->Left);PreorderTraverse(T->Righ); }void InOrderTraverse(TreeNode* T) {if (T == NULL) return;InOrderTraverse(T->Left);printf("%c ", T->ch);InOrderTraverse(T->Righ); }void PostOrderTraverse(TreeNode* T) {if (T == NULL) return;PostOrderTraverse(T->Left);PostOrderTraverse(T->Righ);printf("%c ", T->ch); }int main() {//二叉树节点 #if 1TreeNode* NodeA = new TreeNode('A');TreeNode* NodeB = new TreeNode('B');TreeNode* NodeC = new TreeNode('C');TreeNode* NodeD = new TreeNode('D');TreeNode* NodeE = new TreeNode('E');TreeNode* NodeF = new TreeNode('F');TreeNode* NodeG = new TreeNode('G');TreeNode* NodeH = new TreeNode('H');TreeNode* NodeI = new TreeNode('I'); #endif//二叉树图解/*A/ \B C/ / \D E F/ \ \G H I*///二叉树关联 #if 1NodeA->Left = NodeB;NodeB->Left = NodeD;NodeD->Left = NodeG;NodeD->Righ = NodeH;NodeA->Righ = NodeC;NodeC->Left = NodeE;NodeE->Righ = NodeI;NodeC->Righ = NodeF; #endif//二叉树遍历 #if 1PreorderTraverse(NodeA);InOrderTraverse(NodeA);PostOrderTraverse(NodeA); #endifreturn 0; } -
节点增删

-
假如删除节点为叶子节点,直接删除节点并修正父节点对应指向为NULL。
-
假如删除节点存在一个子节点,子节点替换被删除节点位置,并对应指向。
-
假如删除节点存在两个子节点。
//二叉树节点TreeNode* InsertNode = new TreeNode('J');TreeNode* TempNode = NodeA->Left;NodeA->Left = InsertNode;InsertNode->Left = TempNode;
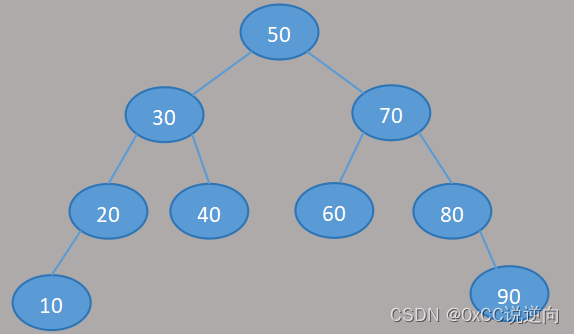
二叉搜索树
-
元素关联
-
根节点的左子树不为空,则左子树上的所有节点的值均小于它根节点的值。
-
根节点的右子树不为空,则右子树上的所有节点的值均大于它根节点的值。
-
根节点的左子树以及右子树均为二叉排序树。
-
-
-
元素排列
-
中序遍历 LDR 左子树 根节点 右子树
-
10 20 30 40 50 60 70 80 90
-

-
-
元素搜索
-
通过根节点按左子节点遍历下去为最小值节点。
-
通过根节点按右子节点遍历下去为最大值节点。
-
查找指定节点二分(左小右大)。
-
-
删除节点
-
删除节点为叶子节点 - 直接删除节点,不会对当前结构产生影响。
-
删除节点仅存在左子树 - 删除节点左子树替换。
-
删除节点仅存在右子树 - 删除节点右子树替换。
-
删除节点同时存在左子树以及右子树 - 删除节点左子树内容挂在删除节点右子树中的左子节点,删除节点的右子节点替换被删除节点。
-
示例代码
#include <iostream>class TreeNode { public:int value;TreeNode* left;TreeNode* right;TreeNode(int Num) : value(Num), left(nullptr), right(nullptr){} };class BinarySearchTree { public://插入节点TreeNode* Insert(TreeNode* Node, int value){//50, 30, 20, 40, 70, 60, 80, 10, 90//空节点if (Node == NULL) return new TreeNode(value);//判断大小if (value < Node->value){Node->left = Insert(Node->left, value);}else{Node->right = Insert(Node->right, value);}return Node;}//中序遍历void InOrderTraverse(TreeNode* Root){if (Root == NULL) return;InOrderTraverse(Root->left);std::cout << Root->value << std::endl;InOrderTraverse(Root->right);}//查找节点TreeNode* Search(TreeNode* Node, int value){if (Node == NULL) return NULL;if (Node->value == value) return Node;if (value < Node->value){return Search(Node->left, value);}else{return Search(Node->right, value);}}//删除节点TreeNode* Delete(TreeNode* Root, int value){if (Root == NULL) return NULL;//删除节点if (Root->value == value){if (Root->left == NULL && Root->right == NULL){delete Root;return NULL;}else if (Root->right == NULL && Root->left != NULL){TreeNode* retNode = Root->left;delete Root;return retNode;}else if (Root->right != NULL && Root->left == NULL){TreeNode* retNode = Root->right;delete Root;return retNode;}else{TreeNode* lastLeft = Root->right;while (lastLeft->left != NULL) lastLeft = lastLeft->left;lastLeft->left = Root->left;TreeNode* deleteNode = Root;Root = Root->right;delete deleteNode;return Root;}}if (Root->value > value){Root->left = Delete(Root->left, value);}if (Root->value < value){Root->right = Delete(Root->right, value);}return NULL;} };int main() {BinarySearchTree BST;TreeNode* Root = NULL;int Arr[] = {30, 20, 40, 35,70, 60, 80, 10, 90 };Root = BST.Insert(Root, 50);for (size_t i = 0; i < sizeof(Arr) / sizeof(Arr[0]); i++){BST.Insert(Root, Arr[i]);}BST.InOrderTraverse(Root);TreeNode* Temp = BST.Search(Root, 35);BST.Delete(Root, 70);return 0; } -
平衡二叉树
-
平衡二叉树
-
二叉排序树。
-
任何一个节点的左子树以及右子树都是平衡二叉树。
-
任何一个节点的左子树与右子树的高度差值的绝对值不能大于一。
-
-
平衡因子
-
节点的平衡因子为其节点左子树的高度减去其右子树的高度(0/1/-1)。
-
-
最小不平衡子树
-
二叉树中插入节点时,距离插入节点位置最近的BF值大于一的节点作为最小不平衡子树。
-
-
节点失衡
-
二叉树插入节点时,出现平衡因子绝对值大于一的最小不平衡子树。
-
通过“旋转”来修正最小不平衡子树。
-
-
旋转方式
-
左旋
-
失衡节点的右子节点作为新的根节点。
-
将失衡节点作为新的根节点的左子节点。
-
新根节点如果存在左子树则转到旧根节点右子树下。
-
-
右旋
-
失衡节点的左子节点作为新的根节点。
-
将失衡节点作为新的根节点的右子节点。
-
新根节点如果存在右子树则转到旧根节点左子树下。
-
-
旋转类型
-
LL(单右旋转)
-
触发 - 插入节点发生在左子树的左侧
-
操作 - 失衡节点的左子节点作为新的根节点,将失衡节点作为新的根节点的右子节点。
-
图解
3 2/ / \2 1 3/ 1- RR(单左旋转)- 触发 - 插入节点发生在右子树的右侧- 操作 - 失衡节点的右子节点作为新的根节点,将失衡节点作为新的根节点的左子节点。- 图解```Objective-C++3 6\ / \6 3 8/ \ \5 8 5
-
-
-
-
模拟旋转
-
30 20 10 40 50 60 70 100 90
-

-

#include <stdio.h> #include <stdlib.h> #include <memory.h>//节点结构 typedef struct _Node {int value;int height;struct _Node* left;struct _Node* right; }Node;//节点高度 int GetNodeHeight(Node* node) {if (node == NULL) return NULL;return node->height; }//平衡因子 int GetNodeBalanceFactor(Node* node) {if (node == NULL) return NULL;return GetNodeHeight(node->left) - GetNodeHeight(node->right); }//左旋处理 Node* LeftRotate(Node* node) {//失衡节点的右子节点作为新的根节点Node* Root = node->right;Node* Temp = Root->left;//将失衡节点作为新的根节点的左子节点Root->left = node;//新根节点如果存在左子树则转到旧根节点右子树下node->right = Temp;//修正节点高度node->height = max(GetNodeHeight(node->left), GetNodeHeight(node->right)) + 1;Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;return Root; }//右旋处理 Node* RightRotate(Node* node) {//失衡节点的左子节点作为新的根节点Node* Root = node->left;Node* Temp = Root->right;//将失衡节点作为新的根节点的右子节点Root->right = node;//新根节点如果存在右子树则转到旧根节点左子树下node->left = Temp;//修正节点高度node->height = max(GetNodeHeight(node->left), GetNodeHeight(node->right)) + 1;Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;return Root; }//创建节点 Node* NewNode(int value) {Node* node = malloc(sizeof(Node));if (node == NULL) return NULL;memset(node, 0, sizeof(Node));node->value = value;node->height = 1;node->left = NULL;node->right = NULL;return node; }//插入节点 Node* Insert(Node* Root, int value) {//空的结构if (Root == NULL) return NewNode(value);//节点关联if (Root->value > value){Root->left = Insert(Root->left, value);}else if (Root->value < value){Root->right = Insert(Root->right, value);}else{return Root;}//节点高度Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;//节点失衡int nBalance = GetNodeBalanceFactor(Root);//左左if (nBalance > 1 && value < Root->left->value){return RightRotate(Root);};//右右if (nBalance < -1 && value > Root->right->value){return LeftRotate(Root);}//左右if (nBalance > 1 && value > Root->left->value){Root->left = LeftRotate(Root->left);return RightRotate(Root);}//右左if (nBalance < -1 && value < Root->right->value){Root->right = RightRotate(Root->right);return LeftRotate(Root);}return Root; }int main() {Node* Root = NULL;Root = Insert(Root, 30);Root = Insert(Root, 20);Root = Insert(Root, 25);return 0; }-
示例代码
-
-
相关文章:

数据结构 - C/C++ - 树
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 树的概念 结构特性 树的样式 树的存储 树的遍历 节点增删 二叉搜索树 平衡二叉树 树的概念 二叉树是树形结构,是一种非线性结构。 非线性结构:在二叉树中&#x…...
Linux源码阅读笔记12-RCU案例分析
在之前的文章中我们已经了解了RCU机制的原理和Linux的内核源码,这里我们要根据RCU机制写一个demo来展示他应该如何使用。 RCU机制的原理 RCU(全称为Read-Copy-Update),它记录所有指向共享数据的指针的使用者,当要修改构想数据时&…...

【C++】双线性差值算法实现RGB图像缩放
双线性差值算法 双线性插值(Bilinear Interpolation)并不是“双线性差值”,它是一种在二维平面上估计未知数据点的方法,通常用于图像处理中的图像缩放。 双线性插值的基本思想是:对于一个未知的数据点,我…...
计算机网络知识普及之四元组
在涉及到TCP/UDP等IP类通信协议时,存在四元组概念 这里只是普及使用 先来一些前置知识,什么是IP协议? IP协议全称为互联网协议,处于网络层中,主要作用是标识网络中的设备,每个设备的IP地址是唯一的。 在网…...

深度探讨网络安全:挑战、防御策略与实战案例
目录 编辑 一、引言 二、网络安全的主要挑战 恶意软件与病毒 数据泄露 分布式拒绝服务攻击(DDoS) 内部威胁 三、防御策略与实战案例 恶意软件防护 网络钓鱼防护 数据泄露防护 总结 一、引言 随着信息技术的迅猛发展,网络安全问…...

“穿越时空的机械奇观:记里鼓车的历史与科技探秘“
在人类文明的发展历程中,科技的创新与进步不仅仅推动了社会的进步,也为我们留下了丰富的文化遗产。记里鼓车,作为一种古老的里程计量工具,其历史地位和技术成就在科技史上具有重要的意义。本文将详细介绍记里鼓车的起源、结构原理…...

DevOps CMDB平台整合Jira工单
背景 在DevOps CMDB平台建设的过程中,我们可以很容易的将业务应用所涉及的云资源(WAF、K8S、虚拟机等)、CICD工具链(Jenkins、ArgoCD)、监控、日志等一次性的维护到CMDB平台,但随着时间的推移,…...
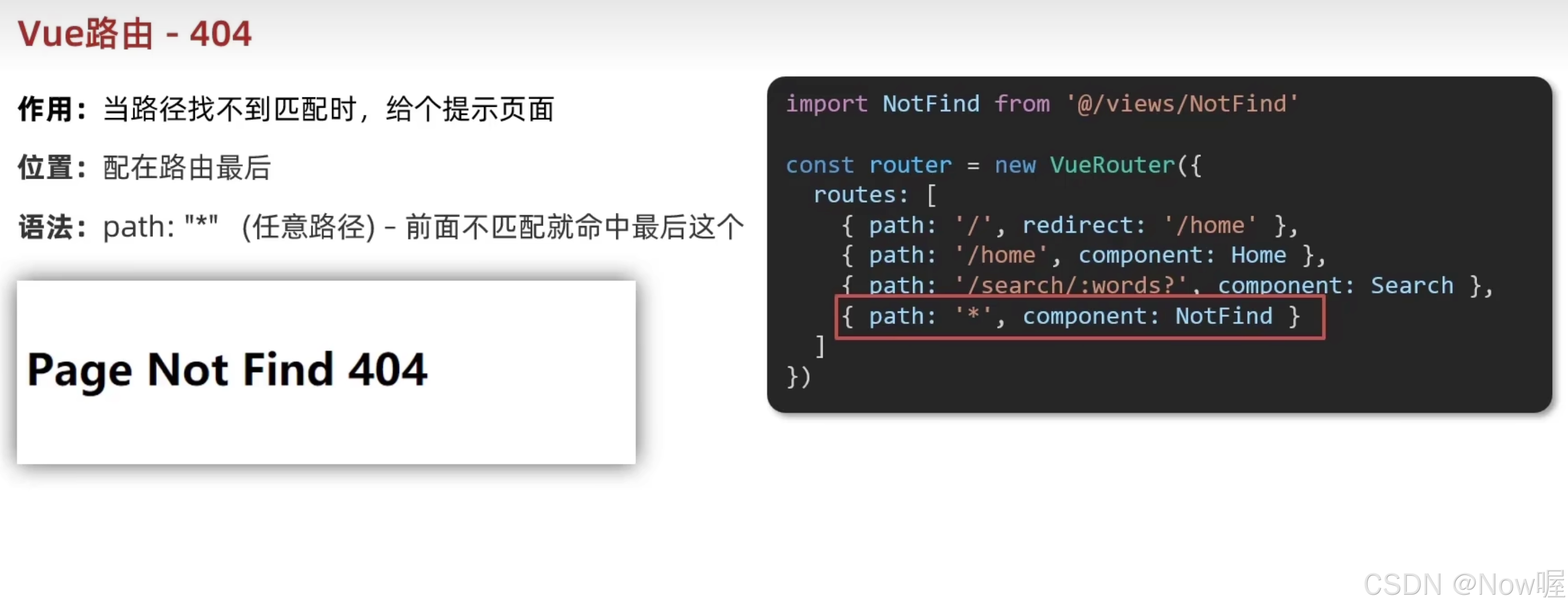
Vue-路由
路由简介 SPA单页面应用。导航区和展示区 单页Web应用整个应用只有一个完整的页面点击页面中的导航连接不会刷新页面,只会做页面的局部更新数据需要通过ajax请求获取 路由:路由就是一组映射关系,服务器接收到请求时,根据请求路…...

【Rust入门教程】安装Rust
文章目录 前言Rust简介Rust的安装更新与卸载rust更新卸载 总结 前言 在当今的编程世界中,Rust语言以其独特的安全性和高效性吸引了大量开发者的关注。Rust是一种系统编程语言,专注于速度、内存安全和并行性。它具有现代化的特性,同时提供了低…...

Character.ai因内容审查流失大量用户、马斯克:Grok-3用了10万块英伟达H100芯片
ChatGPT狂飙160天,世界已经不是之前的样子。 更多资源欢迎关注 1、爆火AI惨遭阉割,1600万美国年轻人失恋?Character.ai被爆资金断裂 美国流行的社交软件Character.ai近期对模型进行大幅度内容审查,导致用户感到失望并开始流失。…...

Spring源码九:BeanFactoryPostProcessor
上一篇Spring源码八:容器扩展一,我们看到ApplicationContext容器通过refresh方法中的prepareBeanFactory方法对BeanFactory扩展的一些功能点,包括对SPEL语句的支持、添加属性编辑器的注册器扩展解决Bean属性只能定义基础变量的问题、以及一些…...

大模型笔记1: Longformer环境配置
论文: https://arxiv.org/abs/2004.05150 目录 库安装 LongformerForQuestionAnswering 库安装 首先保证电脑上配置了git. git环境配置: https://blog.csdn.net/Andone_hsx/article/details/87937329 3.1、找到git安装路径中bin的位置,如:D:\Prog…...
类和对象(提高)
类和对象(提高) 1、定义一个类 关键字class 6 class Data1 7 { 8 //类中 默认为私有 9 private: 10 int a;//不要给类中成员 初始化 11 protected://保护 12 int b; 13 public://公共 14 int c; 15 //在类的内部 不存在权限之分 16 void showData(void)…...

免费最好用的证件照制作软件,一键换底+老照片修复+图片动漫化,吊打付费!
这款软件真的是阿星用过的,最好用的证件照制作软件,没有之一! 我是阿星,今天要给大家安利一款超实用的证件照工具,一键换底,自动排版,免费无广告,让你在家就能轻松搞定证件照&#…...

antfu/ni 在 Windows 下的安装
问题 全局安装 ni 之后,第一次使用会有这个问题 解决 在 powershell 中输入 Remove-Item Alias:ni -Force -ErrorAction Ignore之后再次运行 ni Windows 11 下的 Powershell 环境配置 可以参考 https://github.com/antfu-collective/ni?tabreadme-ov-file#how …...

Linux 生产消费者模型
💓博主CSDN主页:麻辣韭菜💓 ⏩专栏分类:Linux初窥门径⏪ 🚚代码仓库:Linux代码练习🚚 🌹关注我🫵带你学习更多Linux知识 🔝 前言 1. 生产消费者模型 1.1 什么是生产消…...

深入浅出:MongoDB中的背景创建索引
深入浅出:MongoDB中的背景创建索引 想象一下,你正忙于将成千上万的数据塞入你的MongoDB数据库中,你的用户期待着实时的响应速度。此时,你突然想到:“嘿,我应该给这些查询加个索引!” 没错&…...

Spring事务十种失效场景
首先我们要明白什么是事务?它的作用是什么?它在什么场景下在Spring框架下会失效? 事务:本质上是由数据库和程序之间交互的过程中的衍生物,它是一种控制数据的行为规则。有几个特性 1、原子性:执行单元内,要…...

JELR-630HS漏电继电器 30-500mA 导轨安装 约瑟JOSEF
JELR-HS系列 漏电继电器型号: JELR-15HS漏电继电器;JELR-25HS漏电继电器; JELR-32HS漏电继电器;JELR-63HS漏电继电器; JELR-100HS漏电继电器;JELR-120HS漏电继电器; JELR-160HS漏电继电器&a…...

如何实现一个简单的链表或栈结构
实现一个简单的链表或栈结构是面向对象编程中的基础任务。下面我将分别给出链表和栈的简单实现。 链表(单链表)的实现 链表是由一系列节点组成的集合,每个节点都包含数据部分和指向列表中下一个节点的链接(指针或引用࿰…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...