240703_昇思学习打卡-Day15-K近邻算法实现红酒聚类
KNN(K近邻)算法实现红酒聚类
K近邻算法,是有监督学习中的分类算法,可以用于分类和回归,本篇主要讲解其在分类上的用途。
文章目录
- KNN(K近邻)算法实现红酒聚类
- 算法原理
- 数据下载
- 数据读取与处理
- 模型构建--计算距离
- 模型预测
算法原理
KNN算法虽然是机器学习算法,但是他不学习,他的原理是把所有的训练集都存储下来,在测试的时候把测试集放到原图里面,根据测试点和训练集的距离判定属于的类别。如下图示例,假设我们现在有两个类别,分别是A和B,用三角和圆圈(不太圆见谅)表示,我们把这两种类别都画在坐标系中。此时载入一个未知类别方框,我们的KNN算法就开始了。

首先我们要指定一个K值,K值就是距离值,比如我们先指定K=2,就可以在这个位置类别周围画一个圆(可以理解为半径为2),如下图:
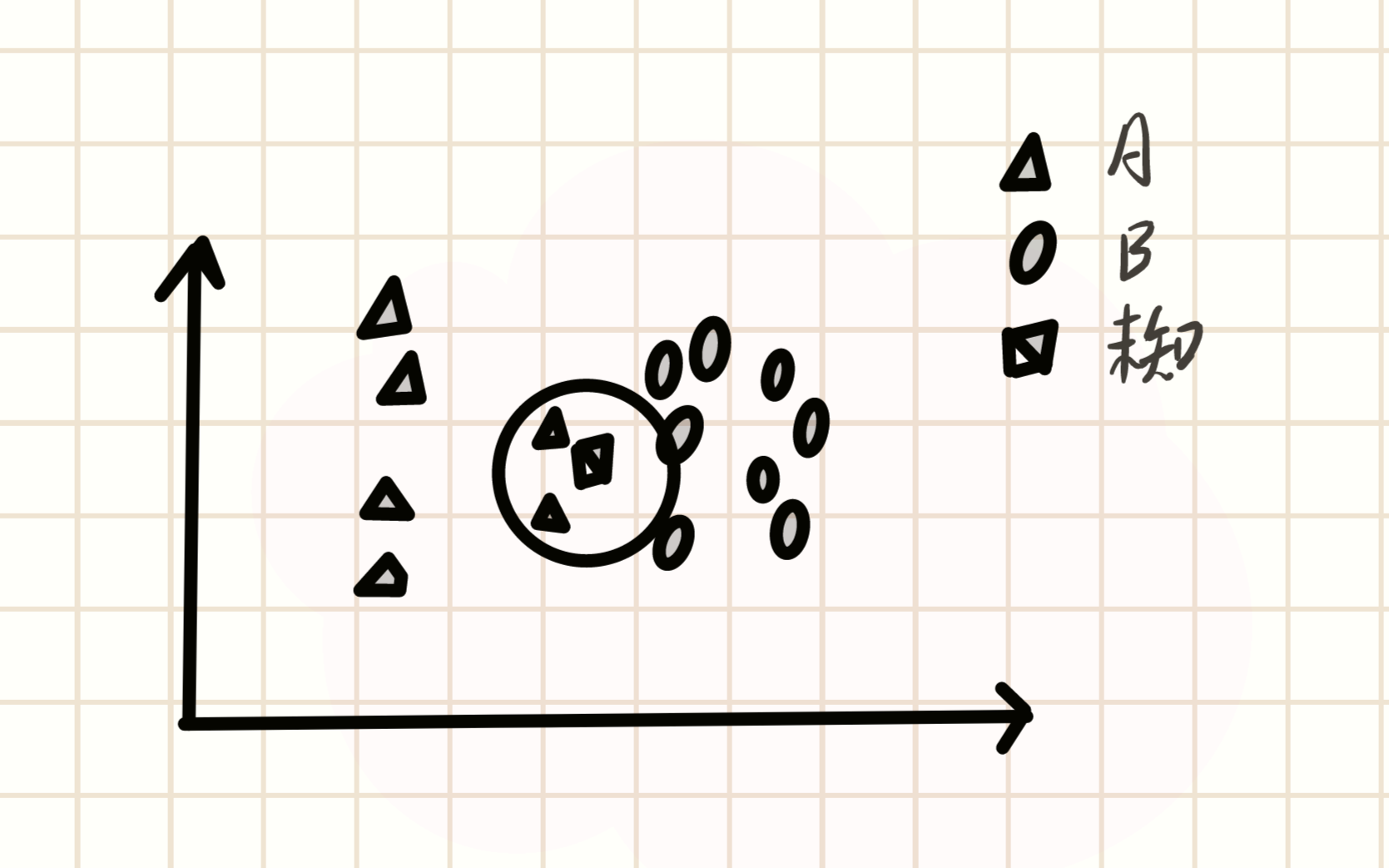
此时我们这个圆框进去了两个A类别,根据算法原理,此时就会把这个未知类别判断为A类别。而如果我们扩大K值呢

当我们把K值从2扩大到4时(小圆外面的大圆),可以看到,此时包进来了4个B类别值,A类别值仍然只有2个,此时就会判断为B类别。这个算法有一点划地盘的意思,画个圈,这圈里谁人多,你就跟谁走,是这意思。歪理原理就这么结束了,下面让我们看看正经的解释。
K近邻算法(K-Nearest-Neighbor, KNN)是一种用于分类和回归的非参数统计方法,最初由 Cover和Hart于1968年提出(Cover等人,1967),是机器学习最基础的算法之一。它正是基于以上思想:要确定一个样本的类别,可以计算它与所有训练样本的距离,然后找出和该样本最接近的k个样本,统计出这些样本的类别并进行投票,票数最多的那个类就是分类的结果。KNN的三个基本要素:
- K值,一个样本的分类是由K个邻居的“多数表决”确定的。K值越小,容易受噪声影响,反之,会使类别之间的界限变得模糊。
- 距离度量,反映了特征空间中两个样本间的相似度,距离越小,越相似。常用的有Lp距离(p=2时,即为欧式距离)、曼哈顿距离、海明距离等。
- 分类决策规则,通常是多数表决,或者基于距离加权的多数表决(权值与距离成反比)。
预测算法(分类)的流程如下:
(1)在训练样本集中找出距离待测样本x_test最近的k个样本,并保存至集合N中;
(2)统计集合N中每一类样本的个数𝐶𝑖,𝑖=1,2,3,…,𝑐𝐶𝑖,𝑖=1,2,3,…,𝑐;
(3)最终的分类结果为argmax𝐶𝑖𝐶𝑖 (最大的对应的𝐶𝑖𝐶𝑖)那个类。
在上述实现过程中,k的取值尤为重要。它可以根据问题和数据特点来确定。在具体实现时,可以考虑样本的权重,即每个样本有不同的投票权重,这种方法称为带权重的k近邻算法,它是一种变种的k近邻算法。
数据下载
我们使用Wine数据集进行展示,Wine数据集的官网:Wine Data Set,这个数据集是对同一地区三个不同品种的葡萄酒进行化学分析后记录的结果。数据集分析了三种葡萄酒中每种所含13种成分的量。这些13种属性是
- Alcohol,酒精
- Malic acid,苹果酸
- Ash,灰
- Alcalinity of ash,灰的碱度
- Magnesium,镁
- Total phenols,总酚
- Flavanoids,类黄酮
- Nonflavanoid phenols,非黄酮酚
- Proanthocyanins,原花青素
- Color intensity,色彩强度
- Hue,色调
- OD280/OD315 of diluted wines,稀释酒的OD280/OD315
- Proline,脯氨酸
可以采用两种下载方式:
- 方式一,从Wine数据集官网下载wine.data文件。
- 方式二,从华为云OBS中下载wine.data文件。
此时我们默认已经安装了Mindspore环境,采用从华为云OBS中下载数据集
from download import download# 下载红酒数据集
url = "https://ascend-professional-construction-dataset.obs.cn-north-4.myhuaweicloud.com:443/MachineLearning/wine.zip"
path = download(url, "./", kind="zip", replace=True)
数据读取与处理
数据下载下来了,我们就进行读取和预处理呗。
%matplotlib inline
import os
import csv
import numpy as np
import matplotlib.pyplot as pltimport mindspore as ms
from mindspore import nn, opsms.set_context(device_target="CPU")
with open('wine.data') as csv_file:data = list(csv.reader(csv_file, delimiter=','))
print(data[56:62]+data[130:133])
执行完这几行代码后我们会打印出来部分数据进行查看,比如我这里打印出这样的数据

此时最开始的每个list最开始的第一个数都是1或2或3,这就是葡萄酒的三种类别,后面紧跟着的13个参数就是他的13种化学成分。
取三类样本(共178条),将数据集的13个属性作为自变量X,将数据集的3个类别作为因变量Y。此时X和Y的值可以自行打印查看
X = np.array([[float(x) for x in s[1:]] for s in data[:178]], np.float32)
Y = np.array([s[0] for s in data[:178]], np.int32)
取样本的某两个属性进行2维可视化,可以看到在某两个属性上样本的分布情况以及可分性。
attrs = ['Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols','Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue','OD280/OD315 of diluted wines', 'Proline']
plt.figure(figsize=(10, 8))
for i in range(0, 4):plt.subplot(2, 2, i+1)# 选择的化学成分由循环轮数i决定a1, a2 = 2 * i, 2 * i + 1# 选择前59个类别为1的数据,化学成分选a1和a2类plt.scatter(X[:59, a1], X[:59, a2], label='1')plt.scatter(X[59:130, a1], X[59:130, a2], label='2')plt.scatter(X[130:, a1], X[130:, a2], label='3')plt.xlabel(attrs[a1])plt.ylabel(attrs[a2])plt.legend()
plt.show()
这里执行完了就可以看到四张打印出来的图,就体现了每一类葡萄酒其中两种化学成分的关系
将数据集按128:50划分为训练集(已知类别样本)和验证集(待验证样本):
train_idx = np.random.choice(178, 128, replace=False)
test_idx = np.array(list(set(range(178)) - set(train_idx)))
X_train, Y_train = X[train_idx], Y[train_idx]
X_test, Y_test = X[test_idx], Y[test_idx]
模型构建–计算距离
利用MindSpore提供的tile, square, ReduceSum, sqrt, TopK等算子,通过矩阵运算的方式同时计算输入样本x和已明确分类的其他样本X_train的距离,并计算出top k近邻
class KnnNet(nn.Cell):def __init__(self, k):super(KnnNet, self).__init__()self.k = kdef construct(self, x, X_train):#平铺输入x以匹配X_train中的样本数x_tile = ops.tile(x, (128, 1))square_diff = ops.square(x_tile - X_train)square_dist = ops.sum(square_diff, 1)dist = ops.sqrt(square_dist)#-dist表示值越大,样本就越接近values, indices = ops.topk(-dist, self.k)return indicesdef knn(knn_net, x, X_train, Y_train):x, X_train = ms.Tensor(x), ms.Tensor(X_train)indices = knn_net(x, X_train)topk_cls = [0]*len(indices.asnumpy())for idx in indices.asnumpy():topk_cls[Y_train[idx]] += 1cls = np.argmax(topk_cls)return cls
模型预测
在验证集上验证KNN算法的有效性,取𝑘=5𝑘=5,验证精度接近80%,说明KNN算法在该3分类任务上有效,能根据酒的13种属性判断出酒的品种。
acc = 0
knn_net = KnnNet(5)
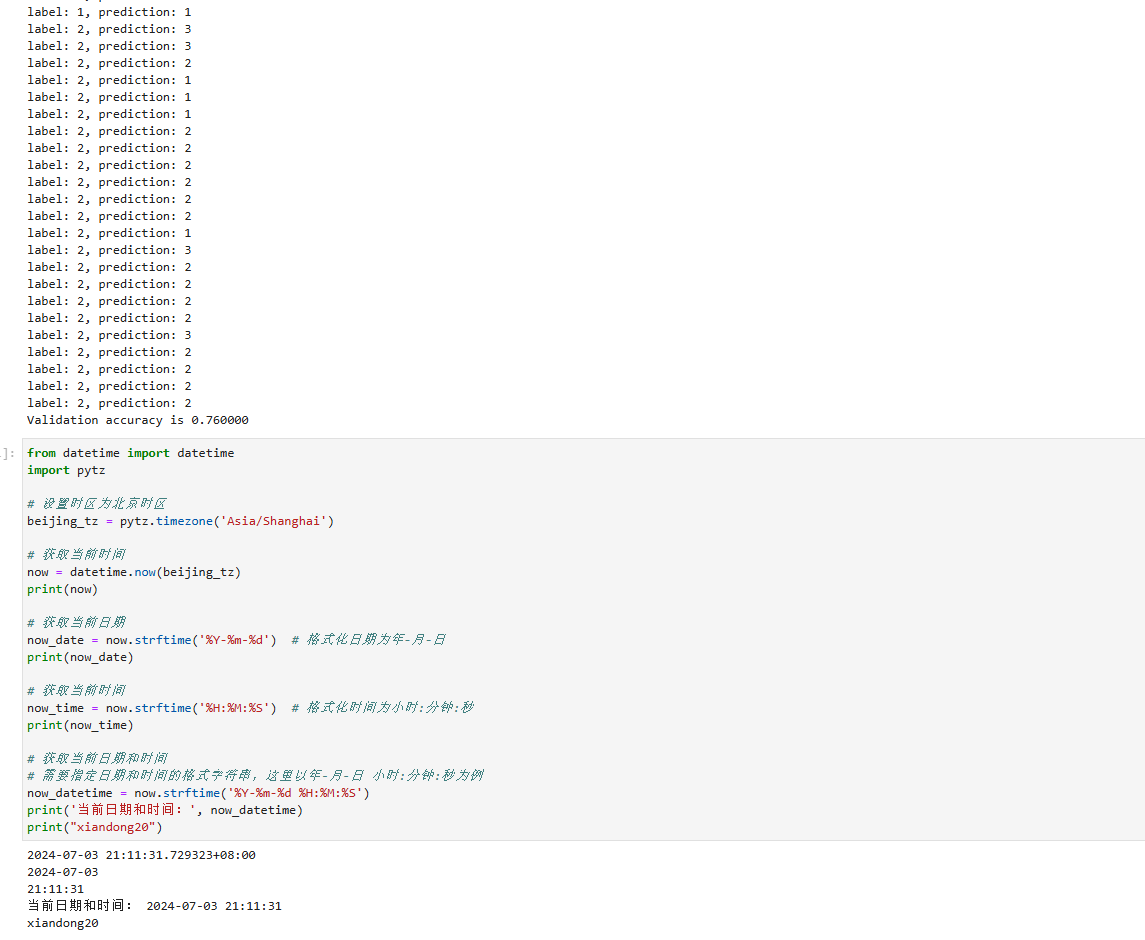
for x, y in zip(X_test, Y_test):pred = knn(knn_net, x, X_train, Y_train)acc += (pred == y)print('label: %d, prediction: %s' % (y, pred))
print('Validation accuracy is %f' % (acc/len(Y_test)))
打卡图片:
相关文章:

240703_昇思学习打卡-Day15-K近邻算法实现红酒聚类
KNN(K近邻)算法实现红酒聚类 K近邻算法,是有监督学习中的分类算法,可以用于分类和回归,本篇主要讲解其在分类上的用途。 文章目录 KNN(K近邻)算法实现红酒聚类算法原理数据下载数据读取与处理模型构建--计算距离模型预测 算法原理 KNN算法虽…...
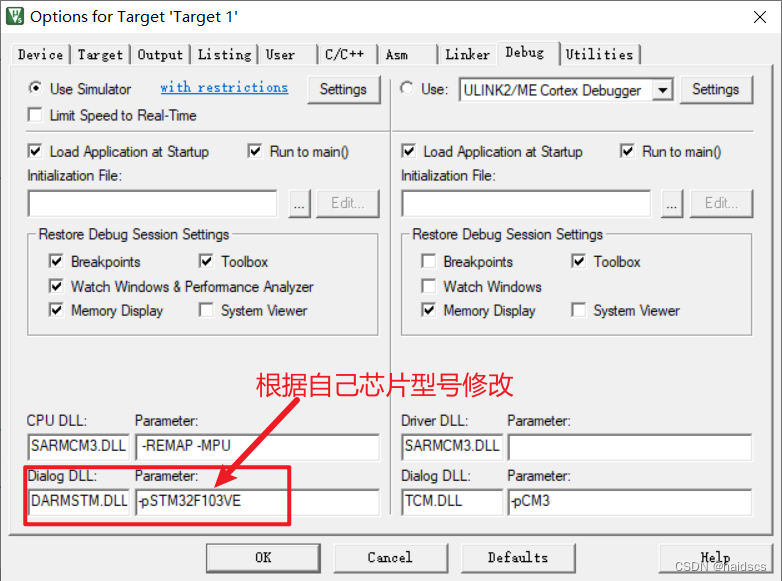
keil5模拟 仿真 报错没有读写权限
debug*** error 65: access violation at 0x4002100C : no write permission 修改为: Dialog DLL默认是DCM3.DLL Parameter默认是-pCM3 应改为 Dialog DLL默认是DARMSTM.DLL Parameter默认是-pSTM32F103VE...
)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号) 文章目录 力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)一、78. 子集二、105. 从前序与中序遍历序列构造二叉树三、43. 字符串相乘四、155. …...

高薪程序员必修课-Java中 Synchronized锁的升级过程
目录 前言 锁的升级过程 1. 偏向锁(Biased Locking) 原理: 示例: 2. 轻量级锁(Lightweight Locking) 原理: 示例: 3. 重量级锁(Heavyweight Locking)…...

Vue项目打包上线
Nginx 是一个高性能的开源HTTP和反向代理服务器,也是一个IMAP/POP3/SMTP代理服务器。它在设计上旨在处理高并发的请求,是一个轻量级、高效能的Web服务器和反向代理服务器,广泛用于提供静态资源、负载均衡、反向代理等功能。 1、下载nginx 2、…...

算法题中常用的C++功能
文章目录 集合优先队列双端队列排序时自定义比较函数最大数值字符串追加:删除:子串: 元组vector查找创建和初始化赋值: 字典map引入头文件定义和初始化插入元素访问元素更新元素删除元素检查元素存在遍历元素int和string转换 集合…...

左扰动和右扰动
在SLAM(Simultaneous Localization and Mapping)中,使用左扰动还是右扰动主要取决于你如何定义坐标系和你希望扰动影响的姿态表示。这通常与你的坐标系选择和你正在解决的具体问题有关。 左扰动通常用于以下情况: 当你使用局部坐…...

【计算机网络】期末复习(2)
目录 第一章:概述 第二章:物理层 第三章:数据链路层 第四章:网络层 第五章:传输层 第一章:概述 三大类网络 (1)电信网络 (2)有线电视网络 ࿰…...

ojdbc8-full Oracle JDBC 驱动程序的一个完整发行版各文件的功能
文章目录 1. ojdbc8.jar2. ons.jar -3. oraclepki.jar -4. orai18n.jar -5. osdt_cert.jar -6. osdt_core.jar -7. ojdbc.policy -8. README.txt -9. simplefan.jar -10. ucp.jar -11. xdb.jar - ojdbc8-full 是 Oracle JDBC 驱动程序的一个完整发行版,包含了连接和…...
,可能会遇到表被锁定的问题。)
在Linux环境下使用sqlite3时,如果尝试对一个空表进行操作(例如插入数据),可能会遇到表被锁定的问题。
在Linux环境下使用sqlite3时,如果尝试对一个空表进行操作(例如插入数据),可能会遇到表被锁定的问题。这通常是因为sqlite3在默认情况下会对空表进行“延迟创建”,即在实际需要写入数据之前,表不会被真正创建…...

【目标检测】DINO
一、引言 论文: DINO: DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection 作者: IDEA 代码: DINO 注意: 该算法是在Deformable DETR、DAB-DETR、DN-DETR基础上的改进,在学习该算法前&#…...
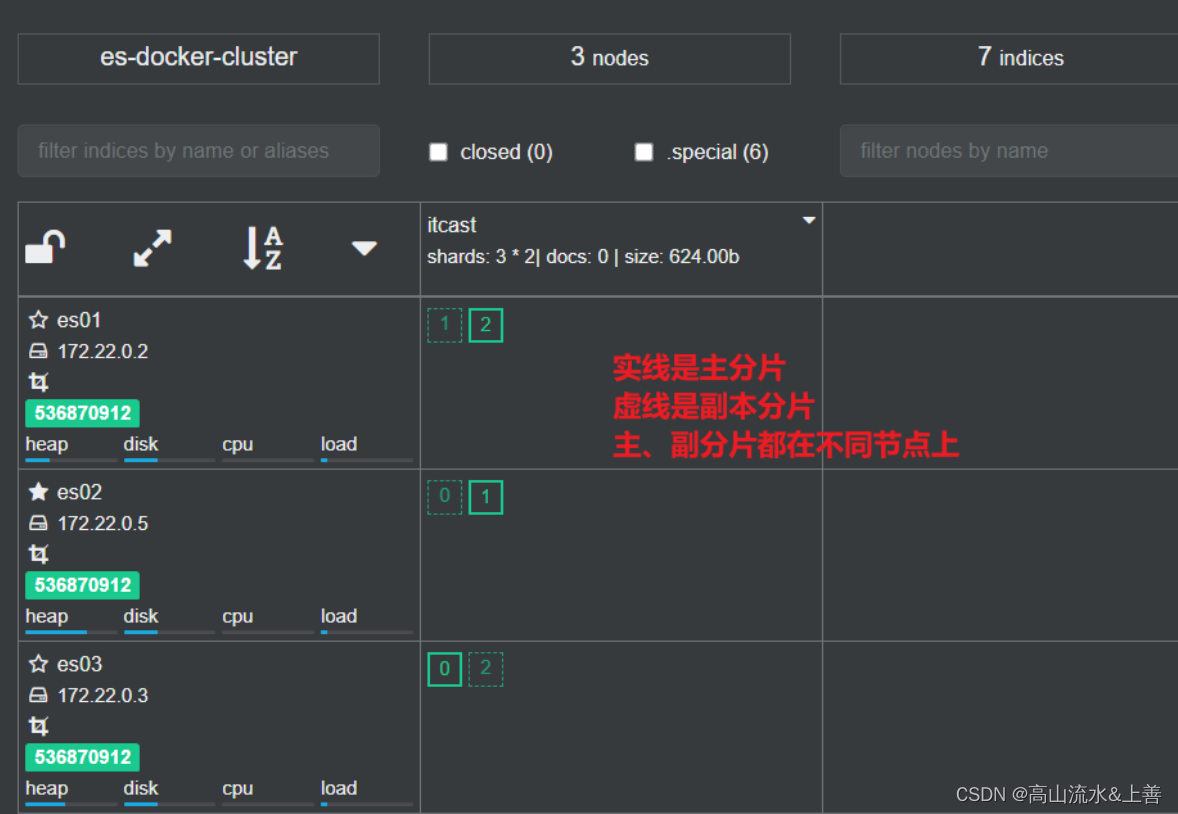
一文包学会ElasticSearch的大部分应用场合
ElasticSearch 官网下载地址:Download Elasticsearch | Elastic 历史版本下载地址1:Index of elasticsearch-local/7.6.1 历史版本下载地址2:Past Releases of Elastic Stack Software | Elastic ElasticSearch的安装(windows) 安装前所…...

创建kobject
1、kobject介绍 kobject的全称是kernel object,即内核对象。每一个kobject都会对应系统/sys/下的一个目录。 2、相关结构体和api介绍 2.1 struct kobject // include/linux/kobject.h 2.2 kobject_create_and_add kobject_create_and_addkobject_createkobj…...

数据结构 - C/C++ - 树
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 树的概念 结构特性 树的样式 树的存储 树的遍历 节点增删 二叉搜索树 平衡二叉树 树的概念 二叉树是树形结构,是一种非线性结构。 非线性结构:在二叉树中&#x…...
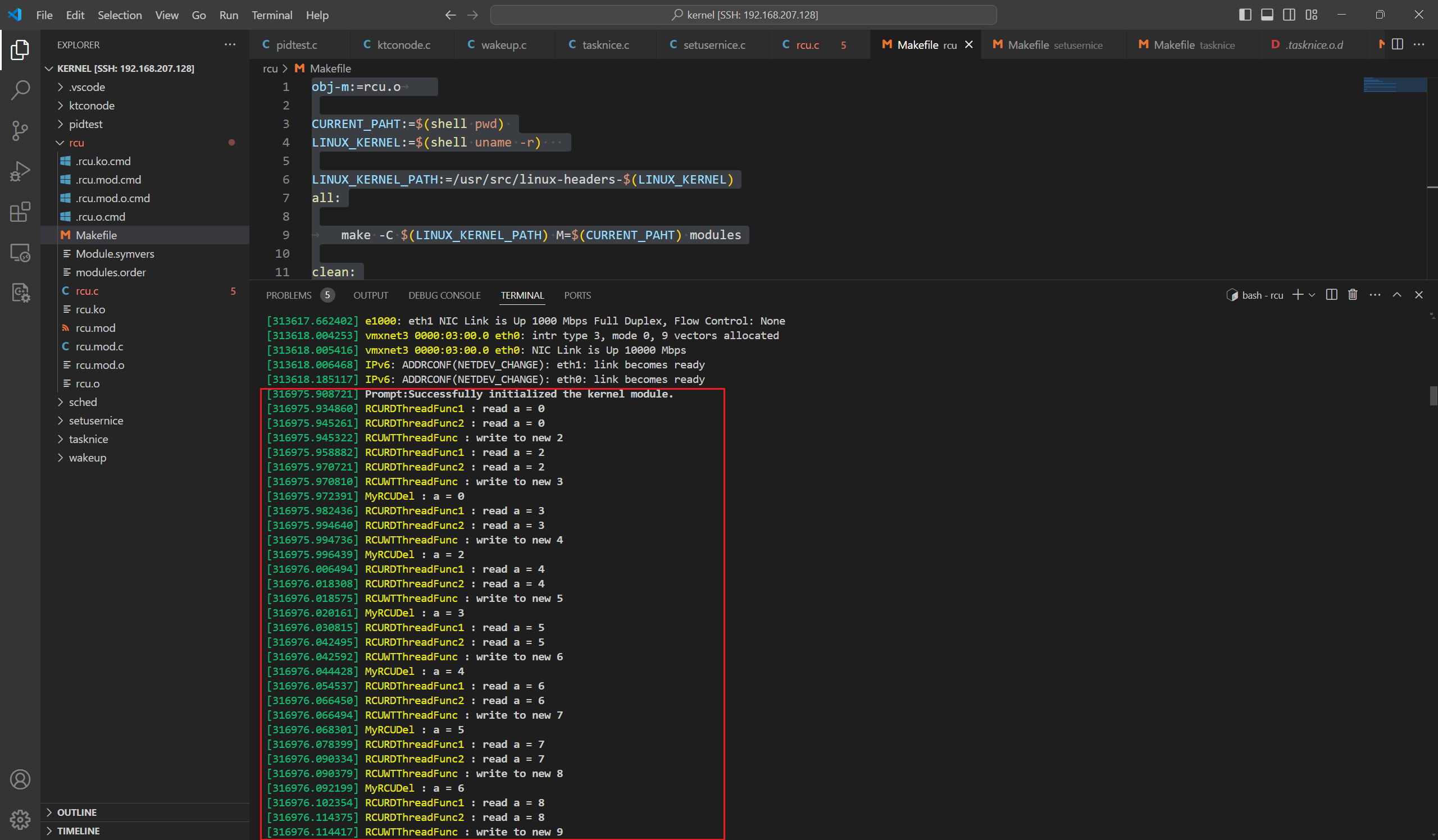
Linux源码阅读笔记12-RCU案例分析
在之前的文章中我们已经了解了RCU机制的原理和Linux的内核源码,这里我们要根据RCU机制写一个demo来展示他应该如何使用。 RCU机制的原理 RCU(全称为Read-Copy-Update),它记录所有指向共享数据的指针的使用者,当要修改构想数据时&…...

【C++】双线性差值算法实现RGB图像缩放
双线性差值算法 双线性插值(Bilinear Interpolation)并不是“双线性差值”,它是一种在二维平面上估计未知数据点的方法,通常用于图像处理中的图像缩放。 双线性插值的基本思想是:对于一个未知的数据点,我…...
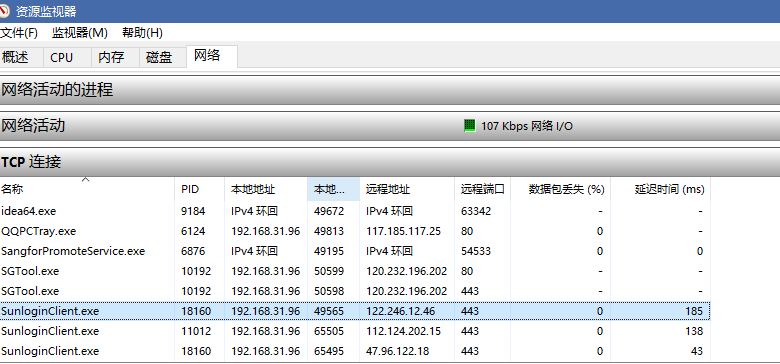
计算机网络知识普及之四元组
在涉及到TCP/UDP等IP类通信协议时,存在四元组概念 这里只是普及使用 先来一些前置知识,什么是IP协议? IP协议全称为互联网协议,处于网络层中,主要作用是标识网络中的设备,每个设备的IP地址是唯一的。 在网…...

深度探讨网络安全:挑战、防御策略与实战案例
目录 编辑 一、引言 二、网络安全的主要挑战 恶意软件与病毒 数据泄露 分布式拒绝服务攻击(DDoS) 内部威胁 三、防御策略与实战案例 恶意软件防护 网络钓鱼防护 数据泄露防护 总结 一、引言 随着信息技术的迅猛发展,网络安全问…...

“穿越时空的机械奇观:记里鼓车的历史与科技探秘“
在人类文明的发展历程中,科技的创新与进步不仅仅推动了社会的进步,也为我们留下了丰富的文化遗产。记里鼓车,作为一种古老的里程计量工具,其历史地位和技术成就在科技史上具有重要的意义。本文将详细介绍记里鼓车的起源、结构原理…...

DevOps CMDB平台整合Jira工单
背景 在DevOps CMDB平台建设的过程中,我们可以很容易的将业务应用所涉及的云资源(WAF、K8S、虚拟机等)、CICD工具链(Jenkins、ArgoCD)、监控、日志等一次性的维护到CMDB平台,但随着时间的推移,…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
