数字信号处理教程(2)——时域离散信号与时域离散系统
上回书说到数字信号处理中基本的一个通用模型框架图。今天咱们继续,可以说今天要讲的东西必须是学习数字信号处理必备的观念——模拟与数字,连续和离散。
时域离散序列
由于数字信号基本都来自模拟信号,所以先来谈谈模拟信号。模拟信号就是常说的连续时域信号,在时间上和幅度上都是连续的,也就是在任何的时刻其都是有值的且值有意义。像日常生活中就有很多连续信号的例子,有温度、压力、水位、化学浓度、电压与电流、位置、速度、加速度、力与扭矩等。如果信号仅在离散时间点上取值有效,这样的信号被称为时域离散信号,也称离散时间信号,用x(n)表示,其中变量n是整数值并在时间上代表一些离散时刻,在咱们的MATLAB里面其实简单的一维数组近似就能看成一个离散时间序列。产生离散时间序列的方法,就是采样。举个例子:xₐ=sin(t)表示一个正弦信号,它也是一个连续时间信号。如果对这个信号每隔tₐ时间间隔取一个样点,可表示成x(n)=xₐ(t)|ₜ₌ₙₜₐ=sin(ntₐ)。
接下来,介绍一下一些基本的序列。
单位取样序列δ(n)是最简单也是使用最多的序列之一,仅在n=0时,其值为1,其他各值均为0。它类似于模拟信号中的单位冲激函数δ(t),不同的是δ(t)在t=0时,取值无穷大。单位取样序列和单位冲激函数如图所示。
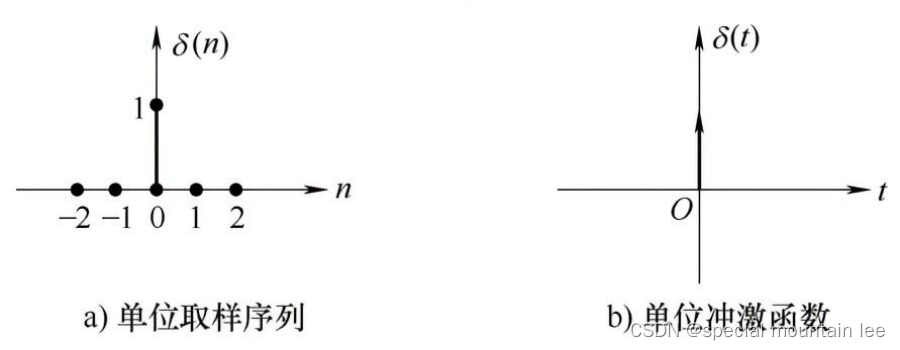
单位阶跃序列u(n)在n≥0时,其值为1;在n<0时,其值为0。和阶跃函数差不多。阶跃函数和冲激函数的关系——u(t)求导是δ(t);映射到离散当中,微分对应的是差分,所以二者关系可以如下图概括。

至于其他的就简单说一下,像矩形序列Rɴ(n)实际上就跟门函数差不多,也可以写成
u(n)-u(n-N),或者是冲激序列的叠加。还有正余弦序列、指数序列这些就不多说了。这里值得大家注意的是所有的序列都能表示成冲激序列的线性组合,而在连续当中,我们绝大多数的情况下用的则是阶梯信号做的近似,实际上两者的意思差不多。满足等式x(n)=x(n+N)(N为正整数)的序列称为周期序列。用这个条件来检验离散时间余弦(或正弦)序列的周期性,即Acos(ωₒn+φ)=Acos[ωₒ(n+N)+φ],不难求出ωₒN=2πk,式中k为整数,也可写成N=2πk/ωₒ,下面讨论N的几种可能情况:周期序列通常分成三种不同的序列。1、当2π/ωₒ为整数时,k=1,则2π/ωₒ即为正弦序列的周期。2、当2π/ωₒ为非整数,但它是一个有理数时,设2π/ωₒ=M/N,其中M和N是互为素数的整数,这时,取k=M,则M为正弦序列的周期。3、当2π/ωₒ为无理数时,此正弦序列为非周期序列。
序列的运算
(一)信号相加
两个信号相加要求长度必须相同。如果两个序列长度不同或者长度相同,但是样本位置不同,也不能相加。可将序列增加若干零值延长,使得序列长度相等且样本位置一致。
(二)信号相乘
信号相乘即两个信号位置相同处的数值相乘,原理与信号相加类似,这里不再举例说明。
(三)信号移位
序列y(n)与x(n)的关系表示为y(n)=x(n-k),其中k为整数。当k>0时,表示序列y(n)是将x(n)向右平移k个单位的结果;当k<0时,表示序列y(n)是将x(n)向左平移k个单位的结果。
(四)信号尺度变换
信号y(n)与x(n)的关系用公式y(n)=x(mn)表示,其中m取整数,表示每隔m单位取一个样本。当然啦,如果说m<0的话,我们就应该要经历反褶这个操作,先后顺序无所谓,全看个人习惯。我一般都是先反褶,在尺度变换。
离散时间系统
说完了离散时间序列,接下来看看离散时间系统,我们通常用T[.]来表示系统函数,输入信号用x(n)表示,输出信号用y(n)表示,它们之间的关系可描述为y(n)=T[x(n)]。
一、线性系统
若某个系统的输入信号和输出信号分别用x1(n)和y1(n)来表示,它们之间的关系描述成y1(n)=T[x1(n)]。同理,该系统的输入信号为x2(n)时,输出信号可表示成y2(n)=T[x2(n)],输入信号为ax1(n)+bx2(n)时,输出信号可表示成y(n)=T[ax1(n)+bx2(n)]。当y(n)与y1(n)及y2(n)满足等式y(n)=ay1(n)+by2(n)时,该系统称为线性系统。说的通俗点,看见线性两个字,咋就应该往齐次性和可加性这两方面去想。
二、时不变系统
当输入信号为x(n)时,输出信号用y(n)表示。如果输入为x(n-n0),输出为y(n-n0),即y(n-n0)=T[x(n-n0)],这时,称该系统为时不变系统,此外,我认为由于离散序列多与位的运算有关,我们通常还称其为移不变系统。这里总得来说,信号波形与起点无关。
三、因果系统
如果系统n时刻的输出只与n时刻及以前的输入有关,而与n时刻之后的输入无关,这样的系统称为因果系统。在线性时不变系统中,当n<0时,单位脉冲响应h(n)=0,该系统是因果系统。同样,当一个序列在n<0时,它的数值均为0,则该序列称为因果序列。
常系数差分方程
接下来看看常系数差分方程,实际与常系数微分方程解法差不多,就是用的数据不一样,毕竟一个是连续的,还有一个是离散的。微分方程我们通常要用拉氏变换的方法来求,而这里就要用Z变换方法来求,因为拉氏变换离散之后它就是Z变换。这里之后再讲现在就不多说了。
线性常系数差分方程的求解方法可归纳为下面三种:
(1)经典解法。这类方法类似模拟系统中求微分方程的解法,过程较复杂,简单的说说,其实就是求齐次解和特解,将特解带入差分方程求得它的待定系数,然后将齐次解和特解相加,带入到差分方程当中去,结合边界条件,求得齐次解的系数,而这一结合就是完全解了。
(2)递推法。此方法简单,适用于计算机求解,这个方法说的高大上,要用递归算法,其实就跟我们高中学的等比数列差不多。
(3)变换域法。将时域转换到z域中求解,方法简单易行,当起始状态为零的情况,所得到就是零状态解;当输入为零的时候,就是零输入响应了。之后将详细说明。
AD转换与DA转换
要通过数字方法处理模拟信号,有必要先将它们转换成数字形式,即转换成具有有限精度的数字序列,这一过程称为模数(A/D)转换,而相应的设备称为A/D转换器(ADC)。下图为AD转换器的基本框架。
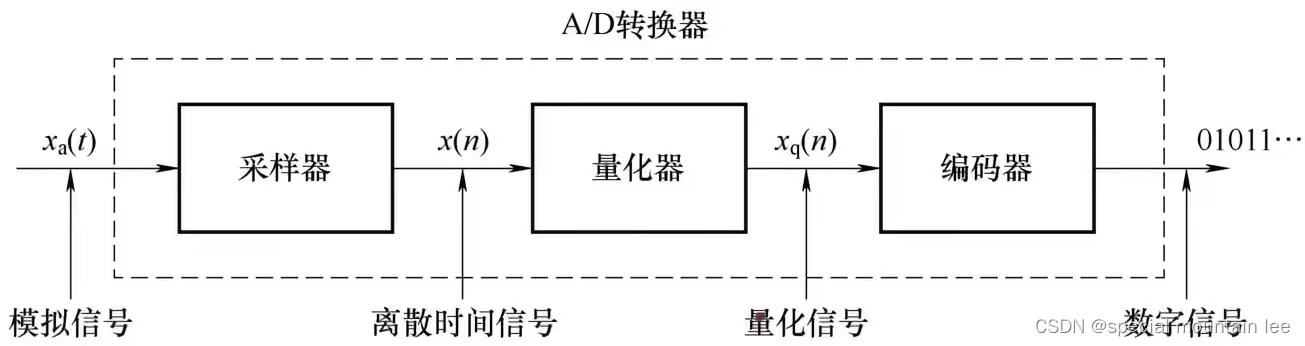
大概以下几个步骤:
(1)采样:采样是连续时间信号到离散时间信号的转换过程,通过对连续时间信号在离散时间点处取样本值获得。因此,如果xₐ(n)是采样器的输入,那么输出是xₐ(nT)=x(n),其中T称为采样间隔,这个是采样最基本的操作,每隔T个位置取个数,当然还有非均匀采样,这里不说了,以后再说。
(2)量化:量化是离散时间连续值信号转换到离散时间离散值(数字)信号的过程。每个信号样本值是从可能值的有限集中选取的。未量化样本x(n)和量化输出xₚ(n)之间的差称为量化误差。
(3)编码:在编码过程中,每一个离散值xₚ(n)由b位的二进制序列表示。
在实际应用的很多场合(例如,语音处理),需要将处理的数字信号转化成模拟信号。将数字信号转化成模拟信号的过程是熟知的数模(D/A)转换。所有D/A转换器通过执行某种插值操作将数字信号的各离散点连接起来,其精度依赖于D/A转换过程的质量。
对模拟信号采样有很多方式。在实际中最常使用的采样类型,即周期采样或均匀采样。可以由下列关系式描述:x(n)=xₐ(nT),式中,x(n)是通过对模拟信号xₐ(t)每隔T(s)取样本值获得的离散时间信号。这一过程,在两个连续的样本之间的时间间隔T称为采样周期或采样间隔,其倒数1/T=Fs称为采样率(样本数/s)或采样频率(Hz)。奈奎斯特采样定理常说,为了能够从采样后的离散信号中完全恢复原始的连续信号,采样频率必须大于等于原始信号最高频率的两倍。因此,这里还需要知道两个概念——过采样和欠采样。过采样指的是对少数类样本进行多次重复采样,使得少数类样本的数量增加,从而使得各类别样本数量相对平衡。过采样可以通过随机复制少数类样本,或者使用更复杂的算法生成新的少数类样本来实现。欠采样则是从多数类样本中随机选择一部分样本,使得多数类样本数量减少,从而达到各类别样本数量相对平衡的目的。但欠采样可能会丢失一些多数类样本中的信息。因此,在工程当中多采用的是过采样。
欲知后事如何,且听下回分解。OVO.......
相关文章:

数字信号处理教程(2)——时域离散信号与时域离散系统
上回书说到数字信号处理中基本的一个通用模型框架图。今天咱们继续,可以说今天要讲的东西必须是学习数字信号处理必备的观念——模拟与数字,连续和离散。 时域离散序列 由于数字信号基本都来自模拟信号,所以先来谈谈模拟信号。模拟信号就是…...

imx6ull/linux应用编程学习(8)PWM应用编程(基于正点)
1.应用层如何操控PWM: 与 LED 设备一样, PWM 同样也是通过 sysfs 方式进行操控,进入到/sys/class/pwm 目录下 这里列举出了 8 个以 pwmchipX(X 表示数字 0~7)命名的文件夹,这八个文件夹其实就对应了…...

等保2.0 实施方案
一、引言 随着信息技术的广泛应用,网络安全问题日益突出,为确保信息系统安全、稳定、可靠运行,保障国家安全、公共利益和个人信息安全,根据《网络安全法》及《信息安全技术 网络安全等级保护基本要求》(等保2.0&#x…...
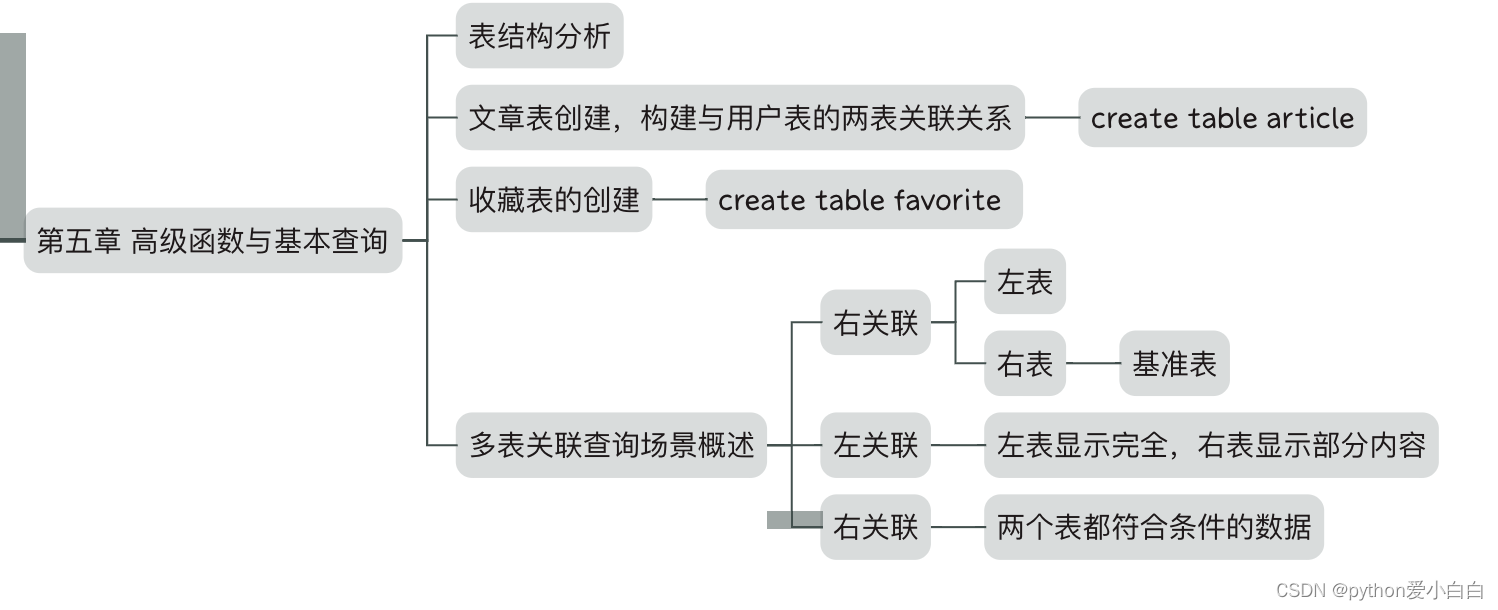
7/3 第六周 数据库的高级查询
...

ubuntu20.04安装kazam桌面屏幕录制工具
在Ubuntu 20.04上安装Kazam可以通过以下步骤进行: 1.打开终端:可以通过按下Ctrl Alt T组合键来打开终端。 2.添加PPA源:Kazam不再在官方Ubuntu仓库中,但可以通过PPA源进行安装。在终端中输入以下命令来添加PPA: su…...

Python应对反爬虫的策略
Python应对反爬虫的策略 概述User-Agent 伪造应对302重定向IP限制与代理使用Cookies和Session管理动态内容加载数据加密与混淆请求频率限制爬虫检测算法法律与道德考量结语 概述 在数字化时代,网络数据采集已成为获取信息的重要手段之一。然而,随着技术…...
240703_昇思学习打卡-Day15-K近邻算法实现红酒聚类
KNN(K近邻)算法实现红酒聚类 K近邻算法,是有监督学习中的分类算法,可以用于分类和回归,本篇主要讲解其在分类上的用途。 文章目录 KNN(K近邻)算法实现红酒聚类算法原理数据下载数据读取与处理模型构建--计算距离模型预测 算法原理 KNN算法虽…...
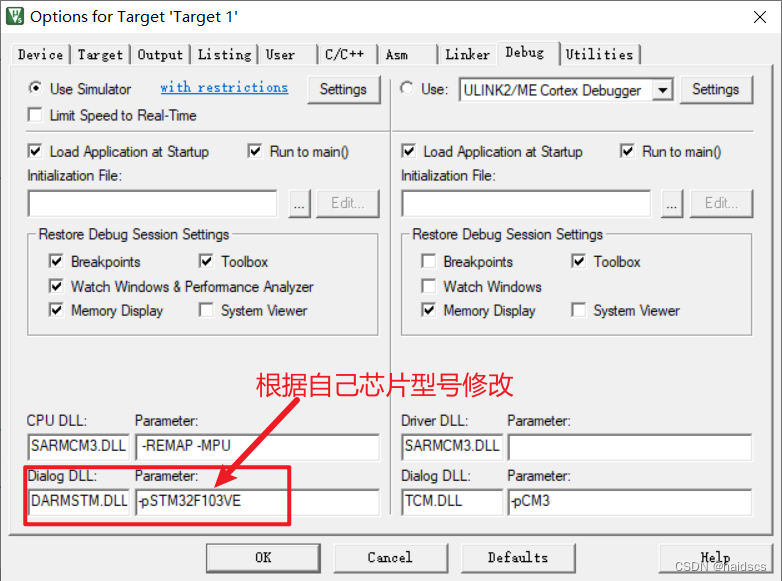
keil5模拟 仿真 报错没有读写权限
debug*** error 65: access violation at 0x4002100C : no write permission 修改为: Dialog DLL默认是DCM3.DLL Parameter默认是-pCM3 应改为 Dialog DLL默认是DARMSTM.DLL Parameter默认是-pSTM32F103VE...
)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号) 文章目录 力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)一、78. 子集二、105. 从前序与中序遍历序列构造二叉树三、43. 字符串相乘四、155. …...

高薪程序员必修课-Java中 Synchronized锁的升级过程
目录 前言 锁的升级过程 1. 偏向锁(Biased Locking) 原理: 示例: 2. 轻量级锁(Lightweight Locking) 原理: 示例: 3. 重量级锁(Heavyweight Locking)…...

Vue项目打包上线
Nginx 是一个高性能的开源HTTP和反向代理服务器,也是一个IMAP/POP3/SMTP代理服务器。它在设计上旨在处理高并发的请求,是一个轻量级、高效能的Web服务器和反向代理服务器,广泛用于提供静态资源、负载均衡、反向代理等功能。 1、下载nginx 2、…...

算法题中常用的C++功能
文章目录 集合优先队列双端队列排序时自定义比较函数最大数值字符串追加:删除:子串: 元组vector查找创建和初始化赋值: 字典map引入头文件定义和初始化插入元素访问元素更新元素删除元素检查元素存在遍历元素int和string转换 集合…...

左扰动和右扰动
在SLAM(Simultaneous Localization and Mapping)中,使用左扰动还是右扰动主要取决于你如何定义坐标系和你希望扰动影响的姿态表示。这通常与你的坐标系选择和你正在解决的具体问题有关。 左扰动通常用于以下情况: 当你使用局部坐…...

【计算机网络】期末复习(2)
目录 第一章:概述 第二章:物理层 第三章:数据链路层 第四章:网络层 第五章:传输层 第一章:概述 三大类网络 (1)电信网络 (2)有线电视网络 ࿰…...

ojdbc8-full Oracle JDBC 驱动程序的一个完整发行版各文件的功能
文章目录 1. ojdbc8.jar2. ons.jar -3. oraclepki.jar -4. orai18n.jar -5. osdt_cert.jar -6. osdt_core.jar -7. ojdbc.policy -8. README.txt -9. simplefan.jar -10. ucp.jar -11. xdb.jar - ojdbc8-full 是 Oracle JDBC 驱动程序的一个完整发行版,包含了连接和…...
,可能会遇到表被锁定的问题。)
在Linux环境下使用sqlite3时,如果尝试对一个空表进行操作(例如插入数据),可能会遇到表被锁定的问题。
在Linux环境下使用sqlite3时,如果尝试对一个空表进行操作(例如插入数据),可能会遇到表被锁定的问题。这通常是因为sqlite3在默认情况下会对空表进行“延迟创建”,即在实际需要写入数据之前,表不会被真正创建…...

【目标检测】DINO
一、引言 论文: DINO: DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection 作者: IDEA 代码: DINO 注意: 该算法是在Deformable DETR、DAB-DETR、DN-DETR基础上的改进,在学习该算法前&#…...
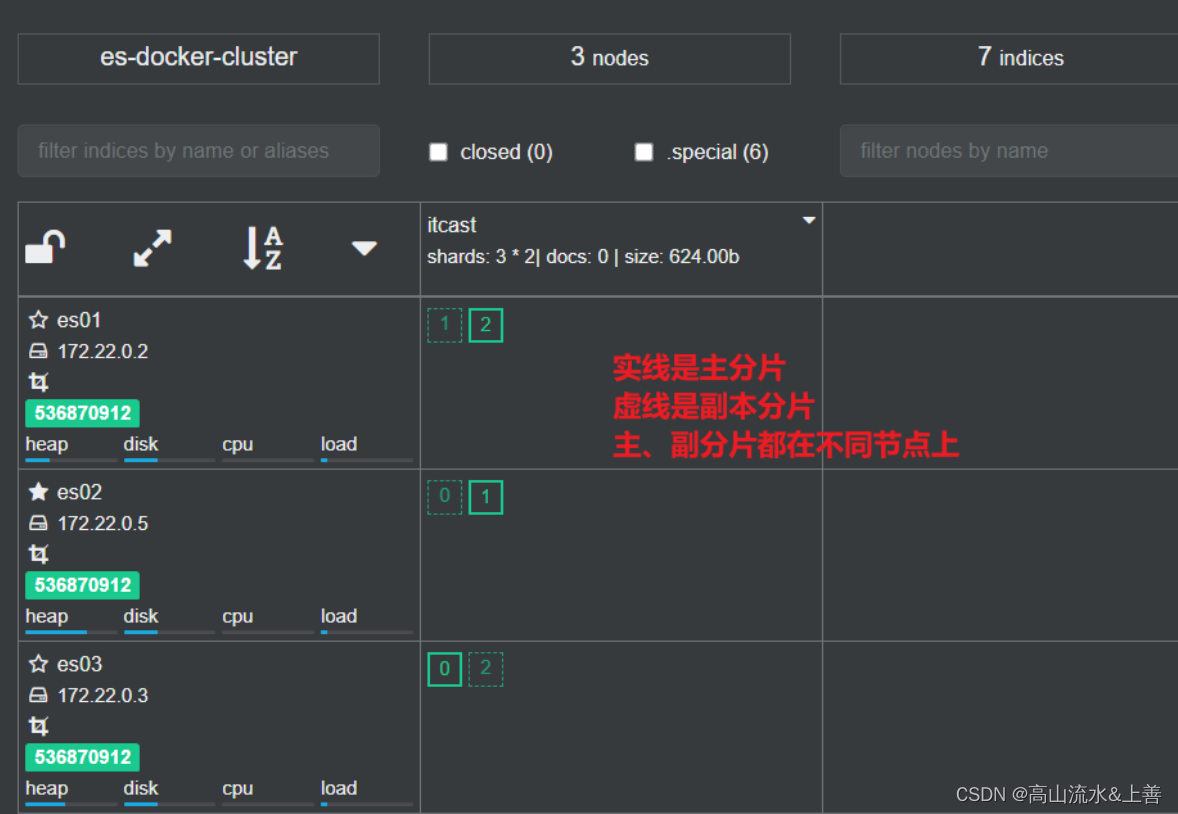
一文包学会ElasticSearch的大部分应用场合
ElasticSearch 官网下载地址:Download Elasticsearch | Elastic 历史版本下载地址1:Index of elasticsearch-local/7.6.1 历史版本下载地址2:Past Releases of Elastic Stack Software | Elastic ElasticSearch的安装(windows) 安装前所…...

创建kobject
1、kobject介绍 kobject的全称是kernel object,即内核对象。每一个kobject都会对应系统/sys/下的一个目录。 2、相关结构体和api介绍 2.1 struct kobject // include/linux/kobject.h 2.2 kobject_create_and_add kobject_create_and_addkobject_createkobj…...

数据结构 - C/C++ - 树
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 树的概念 结构特性 树的样式 树的存储 树的遍历 节点增删 二叉搜索树 平衡二叉树 树的概念 二叉树是树形结构,是一种非线性结构。 非线性结构:在二叉树中&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
