优化Java中XML和JSON序列化
优化Java中XML和JSON序列化
大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!
在Java应用程序中,对于XML和JSON的序列化操作是非常常见的需求。本文将探讨如何通过优化来提升Java中XML和JSON序列化的性能和效率。
1. XML序列化优化技巧
XML序列化通常涉及将Java对象转换为XML格式的字符串,这在Web服务和数据交换中特别常见。以下是一些优化技巧:
package cn.juwatech.serialization;import java.io.StringWriter;
import javax.xml.bind.JAXBContext;
import javax.xml.bind.JAXBException;
import javax.xml.bind.Marshaller;public class XMLSerializer {public String serializeObjectToXML(Object objectToSerialize) throws JAXBException {StringWriter writer = new StringWriter();JAXBContext context = JAXBContext.newInstance(objectToSerialize.getClass());Marshaller marshaller = context.createMarshaller();marshaller.setProperty(Marshaller.JAXB_FORMATTED_OUTPUT, true);marshaller.marshal(objectToSerialize, writer);return writer.toString();}
}
2. JSON序列化优化技巧
与XML类似,JSON序列化将Java对象转换为JSON格式的字符串。以下是一些优化建议:
package cn.juwatech.serialization;import com.fasterxml.jackson.databind.ObjectMapper;
import com.fasterxml.jackson.databind.SerializationFeature;import java.io.IOException;public class JsonSerializer {private static final ObjectMapper objectMapper = new ObjectMapper();public String serializeObjectToJson(Object objectToSerialize) throws IOException {objectMapper.enable(SerializationFeature.INDENT_OUTPUT);return objectMapper.writeValueAsString(objectToSerialize);}
}
3. 性能优化考虑
- 选择合适的库:例如,对于XML序列化可以使用JAXB或者更轻量级的库,如SimpleXML。
- 减少对象层级:复杂对象层级会增加序列化的时间和内存消耗,尽量设计扁平的对象结构。
- 缓存JAXBContext或ObjectMapper实例:这可以减少重复创建对象的开销。
- 避免不必要的序列化:对于不需要传输的数据,可以考虑使用Transient关键字或者自定义序列化过程。
结论
通过本文的优化建议,可以显著提升Java中XML和JSON序列化的性能和效率,使得应用程序在处理大量数据时表现更加优异。务必根据具体需求选择合适的技术和实现方式,以达到最佳的性能和用户体验。
相关文章:

优化Java中XML和JSON序列化
优化Java中XML和JSON序列化 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在Java应用程序中,对于XML和JSON的序列化操作是非常常见的需求。本文将…...
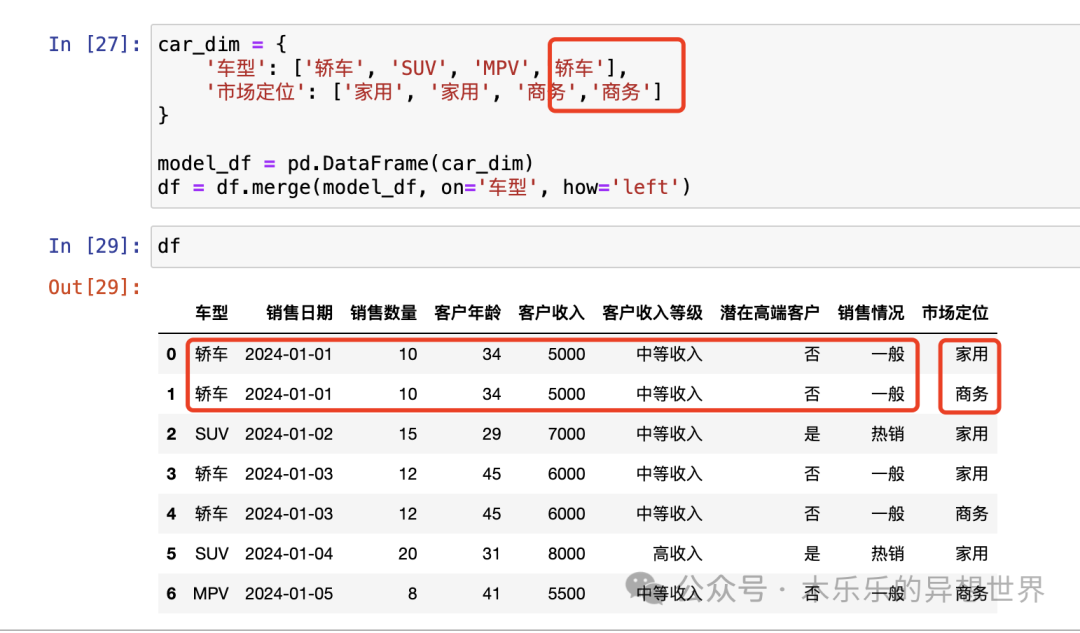
像学Excel 一样学 Pandas系列-创建数据分析维度
嗨,小伙伴们。又到喜闻乐见的Python 数据分析王牌库 Pandas 的学习时间。按照数据分析处理过程,这次轮到了新增维度的部分了。 老样子,我们先来回忆一下,一个完整数据分析的过程,包含哪些部分内容。 其中,…...

Rust 基础教程
Rust 编程语言教程 Rust是一门注重安全、并发和性能的系统编程语言。本文将从Rust的基本语法、常用功能到高级特性,详细介绍Rust的使用方法。 目录 简介环境配置基础语法 变量和常量数据类型函数控制流 所有权和借用 所有权借用 结构体和枚举 结构体枚举 模块和包…...

Study--Oracle-06-Oracler网络管理
一、ORACLE的监听管理 1、ORACLE网络监听配置文件 cd /u01/app/oracle/product/12.2.0/db_1/network/admin 2、在Oracle数据库中,监听器(Listener)是一个独立的进程,它监听数据库服务器上的特定端口上的网络连接请求,…...

uniapp零基础入门Vue3组合式API语法版本开发咸虾米壁纸项目实战
嗨,大家好,我是爱搞知识的咸虾米。 今天给大家带来的是零基础入门uniapp,课程采用的是最新的Vue3组合式API版本,22年发布的uniappVue2版本获得了官方推荐,有很多同学等着我这个vue3版本的那,如果没有学过vu…...
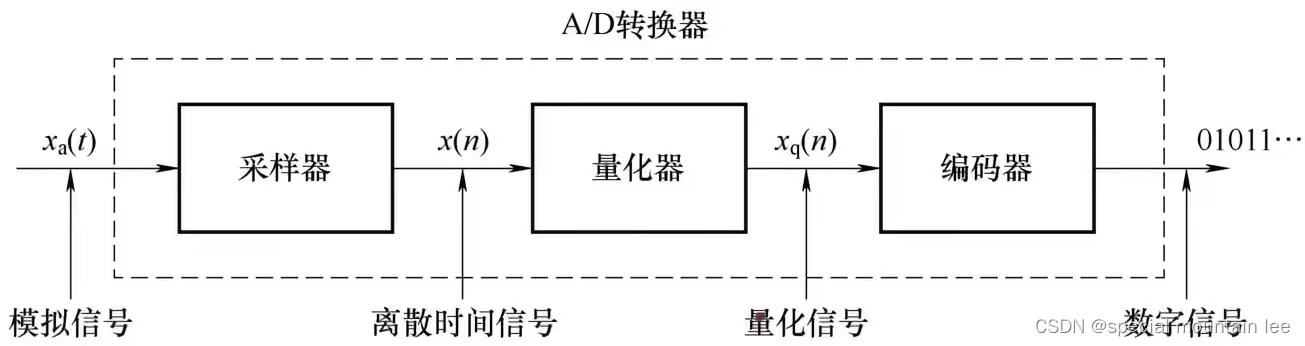
数字信号处理教程(2)——时域离散信号与时域离散系统
上回书说到数字信号处理中基本的一个通用模型框架图。今天咱们继续,可以说今天要讲的东西必须是学习数字信号处理必备的观念——模拟与数字,连续和离散。 时域离散序列 由于数字信号基本都来自模拟信号,所以先来谈谈模拟信号。模拟信号就是…...

imx6ull/linux应用编程学习(8)PWM应用编程(基于正点)
1.应用层如何操控PWM: 与 LED 设备一样, PWM 同样也是通过 sysfs 方式进行操控,进入到/sys/class/pwm 目录下 这里列举出了 8 个以 pwmchipX(X 表示数字 0~7)命名的文件夹,这八个文件夹其实就对应了…...

等保2.0 实施方案
一、引言 随着信息技术的广泛应用,网络安全问题日益突出,为确保信息系统安全、稳定、可靠运行,保障国家安全、公共利益和个人信息安全,根据《网络安全法》及《信息安全技术 网络安全等级保护基本要求》(等保2.0&#x…...
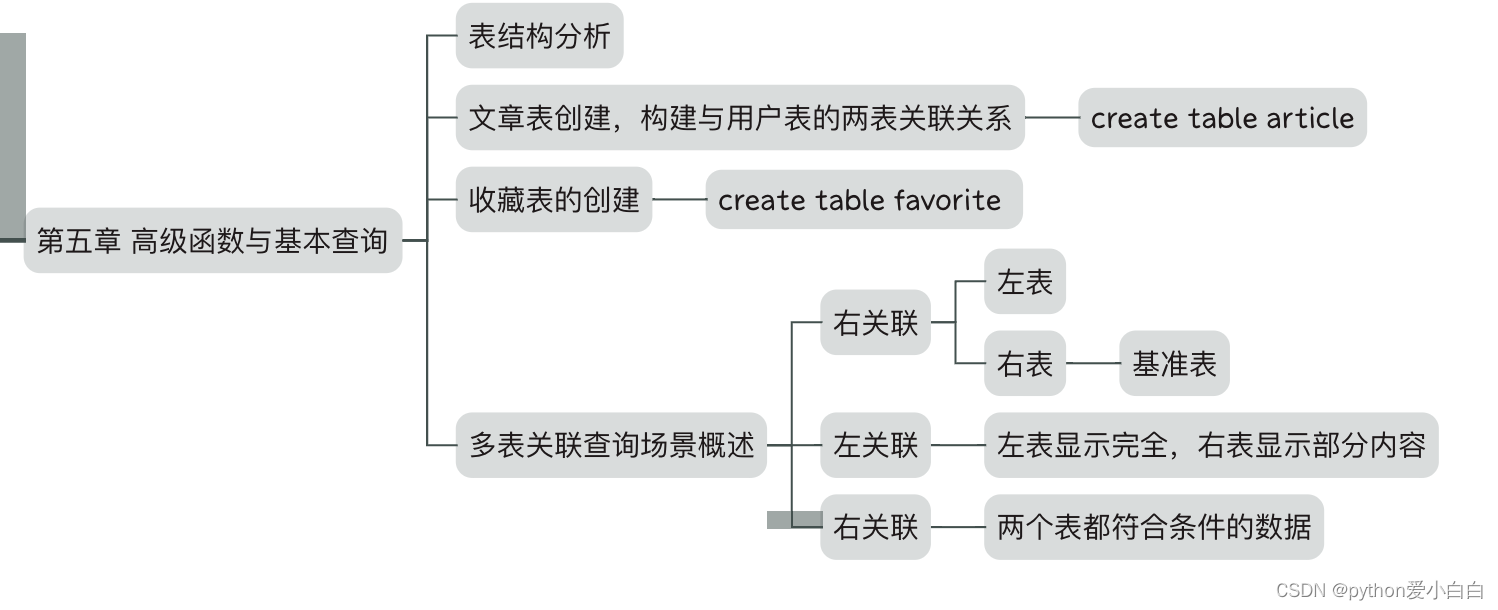
7/3 第六周 数据库的高级查询
...

ubuntu20.04安装kazam桌面屏幕录制工具
在Ubuntu 20.04上安装Kazam可以通过以下步骤进行: 1.打开终端:可以通过按下Ctrl Alt T组合键来打开终端。 2.添加PPA源:Kazam不再在官方Ubuntu仓库中,但可以通过PPA源进行安装。在终端中输入以下命令来添加PPA: su…...

Python应对反爬虫的策略
Python应对反爬虫的策略 概述User-Agent 伪造应对302重定向IP限制与代理使用Cookies和Session管理动态内容加载数据加密与混淆请求频率限制爬虫检测算法法律与道德考量结语 概述 在数字化时代,网络数据采集已成为获取信息的重要手段之一。然而,随着技术…...
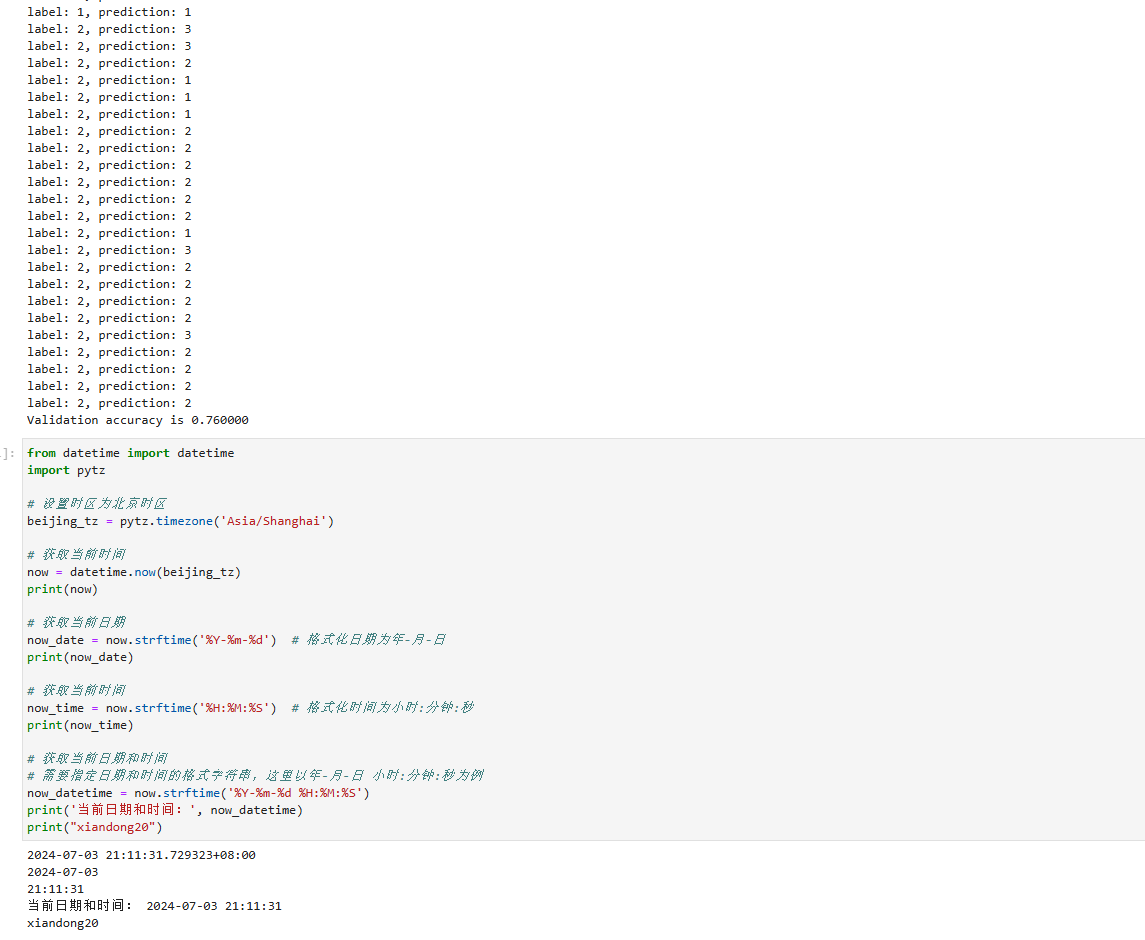
240703_昇思学习打卡-Day15-K近邻算法实现红酒聚类
KNN(K近邻)算法实现红酒聚类 K近邻算法,是有监督学习中的分类算法,可以用于分类和回归,本篇主要讲解其在分类上的用途。 文章目录 KNN(K近邻)算法实现红酒聚类算法原理数据下载数据读取与处理模型构建--计算距离模型预测 算法原理 KNN算法虽…...
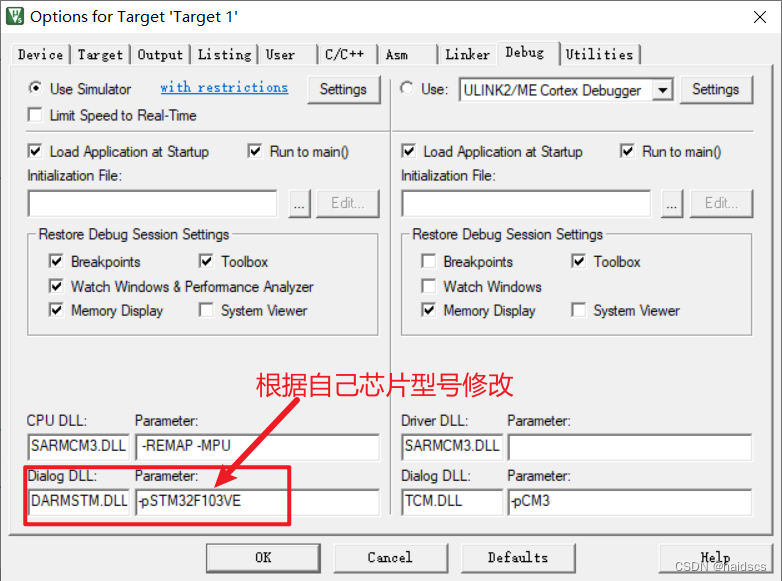
keil5模拟 仿真 报错没有读写权限
debug*** error 65: access violation at 0x4002100C : no write permission 修改为: Dialog DLL默认是DCM3.DLL Parameter默认是-pCM3 应改为 Dialog DLL默认是DARMSTM.DLL Parameter默认是-pSTM32F103VE...
)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)
力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号) 文章目录 力扣爆刷第158天之TOP100五连刷56-60(子集、最小栈、最长有效括号)一、78. 子集二、105. 从前序与中序遍历序列构造二叉树三、43. 字符串相乘四、155. …...

高薪程序员必修课-Java中 Synchronized锁的升级过程
目录 前言 锁的升级过程 1. 偏向锁(Biased Locking) 原理: 示例: 2. 轻量级锁(Lightweight Locking) 原理: 示例: 3. 重量级锁(Heavyweight Locking)…...

Vue项目打包上线
Nginx 是一个高性能的开源HTTP和反向代理服务器,也是一个IMAP/POP3/SMTP代理服务器。它在设计上旨在处理高并发的请求,是一个轻量级、高效能的Web服务器和反向代理服务器,广泛用于提供静态资源、负载均衡、反向代理等功能。 1、下载nginx 2、…...

算法题中常用的C++功能
文章目录 集合优先队列双端队列排序时自定义比较函数最大数值字符串追加:删除:子串: 元组vector查找创建和初始化赋值: 字典map引入头文件定义和初始化插入元素访问元素更新元素删除元素检查元素存在遍历元素int和string转换 集合…...

左扰动和右扰动
在SLAM(Simultaneous Localization and Mapping)中,使用左扰动还是右扰动主要取决于你如何定义坐标系和你希望扰动影响的姿态表示。这通常与你的坐标系选择和你正在解决的具体问题有关。 左扰动通常用于以下情况: 当你使用局部坐…...

【计算机网络】期末复习(2)
目录 第一章:概述 第二章:物理层 第三章:数据链路层 第四章:网络层 第五章:传输层 第一章:概述 三大类网络 (1)电信网络 (2)有线电视网络 ࿰…...

ojdbc8-full Oracle JDBC 驱动程序的一个完整发行版各文件的功能
文章目录 1. ojdbc8.jar2. ons.jar -3. oraclepki.jar -4. orai18n.jar -5. osdt_cert.jar -6. osdt_core.jar -7. ojdbc.policy -8. README.txt -9. simplefan.jar -10. ucp.jar -11. xdb.jar - ojdbc8-full 是 Oracle JDBC 驱动程序的一个完整发行版,包含了连接和…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
