[吃瓜教程]南瓜书第5章神经网络
1.M-P神经元
M-P神经元,全称为McCulloch-Pitts神经元,是一种数学模型,用于模拟生物神经元的功能。这个模型是由Warren McCulloch和Walter Pitts在1943年提出的。它是人工智能和计算神经科学领域中非常重要的早期模型。
M-P神经元接收n个输入(通常来自其他神经元),并给各个输入赋予权重计算加权和,然后和自身特有的阈值 θ \theta θ进行比较(作减法),最后经过激活函数(模拟“抑制”和“激活”)处理得到输出(通常是给下一个神经元)
y = f ( ∑ i = 1 n w i x i − θ ) = f ( w T x + b ) y=f(\sum_{i=1}^nw_ix_i-\theta)=f(w^Tx+b) y=f(i=1∑nwixi−θ)=f(wTx+b)
单个M-P神经元:感知机(sgn作激活函数)、对数几率回归(sigmoid作激活函数)
多个M-P神经元:神经网路
2.感知机(分类模型)
2.1 sgn函数
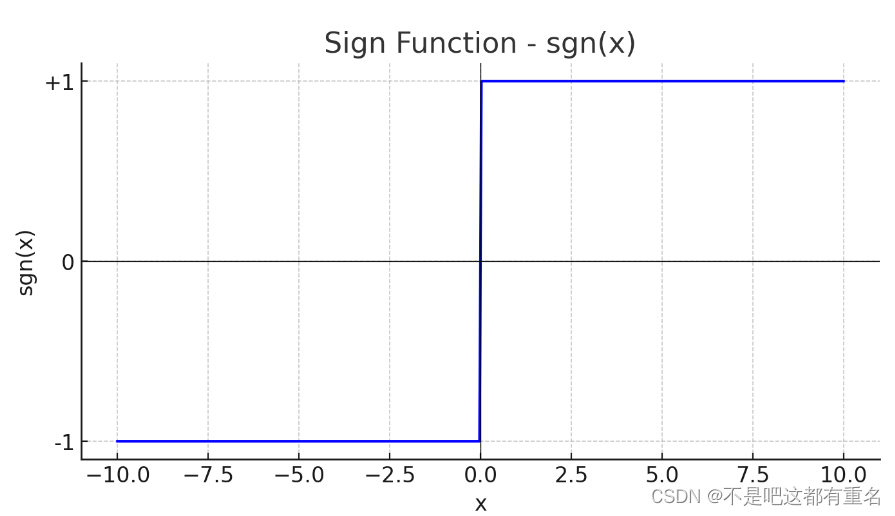
sgn 函数,或称为符号函数(sign function):是一个数学函数,用于确定一个实数的符号。sgn 函数的定义如下:
- 当x>0时,sgn(x)=1
- 当x=0时,sgn(x)=0
- 当x<0时,sgn(x)=-1
图像如下:
2.2 感知机
1)模型
其具体公式如下:
y = s g n ( w T w − θ ) = { 1 , w T x − θ > = 0 0 , w T x − θ < 0 y=sgn(w^Tw-\theta) =\begin{cases} 1& ,{w^Tx-\theta>= 0}\\ 0& ,{w^Tx-\theta<0} \end{cases} y=sgn(wTw−θ)={10,wTx−θ>=0,wTx−θ<0
其中, x ∈ R N x\in \mathbb{R}^N x∈RN为样本的特征向量,是感知机模型的输入, w , θ w,\theta w,θ是感知机模型的参数, w ∈ R n w\in \mathbb{R}^n w∈Rn为权重, θ \theta θ 为阈值
从几何的角度来说,给定一个线性可分的数据集T,感知机的学习目标是求得能对数据集T中的正负样本完全正确划分的超平面,其中 w T x − θ w^Tx-\theta wTx−θ即为超平面方程。
n维空间的超平面 ( w T x + b = 0 , 其中 w , x ∈ R n ) (w^Tx+b=0,其中w,x \in \mathbb R^n) (wTx+b=0,其中w,x∈Rn):
- 超平面方程不唯一
- 法向量w垂直于超平面
- 法向量w和位移项b确定一个唯一超平面
- 法向量w指向的那一半空间为正空间,另一半为负空间
缺点: 只能解决线性可分的问题
模型图如下所示,只包含一个输入层和一个输出层。

2)策略
感知机的学习策略是,随机初始化 w , b w,b w,b,将全体训练样本带入模型找出误分类样本,假设此时误分类样本的集合为 M ⊆ T M\subseteq T M⊆T对任意一个误分类样本 ( x , y ) ∈ M (x,y)\in M (x,y)∈M来说,当 w T x − θ > = 0 w^Tx-\theta >=0 wTx−θ>=0时,模型输出值为 y ^ = 1 \hat y=1 y^=1,样本真实标记为y=0;繁殖,当 w T x − θ < 0 w^Tx-\theta<0 wTx−θ<0时,模型输出值为 y ^ \hat y y^=0,样本真实标记为y=1。综合两种情况可知,以下公式恒成立
( y ^ − y ) ( w T x − θ ) > = 0 (\hat y-y)(w^Tx-\theta)>=0 (y^−y)(wTx−θ)>=0
所以,给定数据集T,其损失函数可以定义为:
L ( w , θ ) = ∑ x ∈ M ( y ^ − y ) ( w T x − θ ) L(w,\theta)=\sum_{x\in M}(\hat y-y)(w^Tx-\theta) L(w,θ)=x∈M∑(y^−y)(wTx−θ)
此时损失函数是非负的。如果没有误分类点,损失函数值为0.而且,误分类点越少,误分类点离超平面越近,损失函数值就越小。
损失函数还可以进一步优化,将 θ \theta θ并入 w w w向量中成为第n+1维0,其中x的第n+1维恒为-1。那么损失函数进一步简化为:
L ( w ) = ∑ x ∈ M ( y ^ − y ) w T x L(w)=\sum_{x\in M}(\hat y-y)w^Tx L(w)=x∈M∑(y^−y)wTx
3)算法
当误分类样本集合M固定时,可以球的损失函数 L ( w ) L(w) L(w)的梯度为
∇ w L ( w ) = ∑ x i ∈ M ( y ^ i − y i ) x i \nabla_wL(w)=\sum_{x_i\in M}(\hat y_i-y_i)x_i ∇wL(w)=xi∈M∑(y^i−yi)xi
学习算法具体采用的是随机梯度下降法,也即极小化过程中不是一次使M中的所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。所以权重 w w w的更新公式为:
w ← w + Δ w w \leftarrow w+\Delta w w←w+Δw
Δ w = − η ( y ^ i − y i ) x i = η ( y i − y ^ i ) x i \Delta w=-\eta(\hat y_i-y_i)x_i=\eta(y_i-\hat y_i)x_i Δw=−η(y^i−yi)xi=η(yi−y^i)xi
其中 η \eta η为学习率,最终解出来的w通常不唯一。
从几何角度方便理解一点,如下图所示,

可以看到红线和绿线都可以把正负样本分开,它们代表了两组 w w w,因此说明解不唯一。
3.神经网络
为了解决线性不可分的数据集(其他的当个神经元的模型也可以结局线性不可分的数据集,只是感知机不可以),提出了由多个神经元构成的神经网络,且用通用近似定理可以证明:只需一个包含足够多神经元的隐层,多层前馈网络(最经典的神经网络之一)就能以任意精度逼近任意复杂度的连续函数。
优点:
既能做回归,也能做分类,而且不需要复杂的特征工程。
需要考虑的问题:
- 对于具体场景,神经网络该做多深,多宽?(没有理论支撑,都是实践经验)
- 对于具体场景,神经网络的结构该如何设计才最合理(没有强理论指导)
- 对于具体场景,神经网络的输出结果该如何解释?(模型的可解释性可以用来指导特征调整)
经典神经网络——多层前馈网络:
每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。

将神经网络(NN)看作一个特征加工函数
x ∈ R d → N N ( x ) → y = x ∗ ∈ R l x\in R^d \rightarrow NN(x) \rightarrow y=x^* \in R^l x∈Rd→NN(x)→y=x∗∈Rl
回归:后面接一个 R l → R R^l \rightarrow R Rl→R的 神经元
y = w T x ∗ + b y=w^Tx^*+b y=wTx∗+b
分类:后面接一个 R l → [ 0 , 1 ] R^l \rightarrow [0,1] Rl→[0,1]的神经元,例如激活函数为sigmoid函数的神经元
y = 1 1 + e − ( w T x ∗ + b ) y=\frac{1}{1+e^{-(w^Tx^*+b)}} y=1+e−(wTx∗+b)1
神经网络可以自动提取特征不用人为的手工设计特征。
神经网络训练方法——BP算法:
在20世纪80年代之前,尽管神经网络已经存在一段时间,但其实际应用受到了限制,主要原因在于无法有效地训练多层神经网络。
在这个背景下,1986年,David E. Rumelhart, Geoffrey E. Hinton, 和 Ronald J. Williams在他们的论文《Learning representations by back-propagating errors》中提出了反向传播算法。这一算法为多层前馈神经网络的训练提供了一个有效的方法,使得神经网络可以在更多复杂问题上展现出强大的表现力。
BP算法是一种基于随机梯度下降的参数更新算法。反向传播算法在处理多层神经网络时,通过链式法则有效地计算梯度,而随机梯度下降则用于基于这些梯度更新权重。反向传播算法与随机梯度下降相辅相成,共同实现了多层神经网络的高效训练。
下面是以输入层第i个神经元与隐层第h个神经元之间的连接全 v i h v_{ih} vih为例推导一下:
损失函数
E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac12\sum^l_{j=1}(\hat y^k_j-y^k_j)^2 Ek=21j=1∑l(y^jk−yjk)2
Δ v i h = − η ∂ E k ∂ v i h \Delta v_{ih}=-\eta \frac{\partial{E_k}}{\partial{v_{ih}}} Δvih=−η∂vih∂Ek
用链式求导得到
∂ E k ∂ v i h = ∑ j = 1 l ∂ E k ∂ y ^ j k ∗ ∂ y ^ j k ∂ β j ∗ ∂ β j ∂ b h ∗ ∂ b h ∂ α h ∗ ∂ α h ∂ v i h \frac{\partial{E_k}}{\partial{v_{ih}}}=\sum^l_{j=1}\frac{\partial{E_k}}{\partial{\hat y^k_j}}*\frac{\partial{\hat y^k_j}}{\partial{\beta_j }}*\frac{\partial{\beta_j }}{\partial{b_h}}*\frac{\partial{b_h}}{\partial{\alpha_h}}*\frac{\partial{\alpha_h}}{\partial{v_{ih}}} ∂vih∂Ek=j=1∑l∂y^jk∂Ek∗∂βj∂y^jk∗∂bh∂βj∗∂αh∂bh∗∂vih∂αh
相关文章:

[吃瓜教程]南瓜书第5章神经网络
1.M-P神经元 M-P神经元,全称为McCulloch-Pitts神经元,是一种数学模型,用于模拟生物神经元的功能。这个模型是由Warren McCulloch和Walter Pitts在1943年提出的。它是人工智能和计算神经科学领域中非常重要的早期模型。 M-P神经元接收n个输入…...

装饰模式解析:基本概念和实例教程
目录 装饰模式装饰模式结构装饰模式应用场景装饰模式优缺点练手题目题目描述输入描述输出描述题解 装饰模式 装饰模式,又称装饰者模式、装饰器模式,是一种结构型设计模式,允许你通过将对象放入包含行为的特殊封装对象中来为原对象绑定新的行…...
)
211.xv6——3(page tables)
在本实验室中,您将探索页表并对其进行修改,以简化将数据从用户空间复制到内核空间的函数。 开始编码之前,请阅读xv6手册的第3章和相关文件: kernel/memlayout.h,它捕获了内存的布局。kernel/vm.c,其中包含…...

yum使用报错:ImportError: /lib64/libxml2.so.2: file too short
系统版本:Rocky 8.10 报错信息: Traceback (most recent call last):File "/usr/lib64/python3.6/site-packages/libdnf/error.py", line 14, in swig_import_helperreturn importlib.import_module(mname)File "/usr/lib64/python3.6/i…...

【Android面试八股文】你是怎么保证Android设备的时间与服务器时间同步的?(使用NTP和TrueTime方案)
文章目录 一、网络时间协议(NTP)二、使用网络时间协议(NTP)2.1 使用系统提供的 NTP 服务器2.2 使用TrueTime2.2.1 引入TrueTime库2.2.2 初始化 TrueTime2.2.3 用法2.2.4 使用 TrueTime 获取时间2.2.4 自动更新时间2.2.5 注意事项二. 使用 HTTP 请求获取服务器时间2.1. 发送…...

解决Python爬虫开发中的数据输出问题:确保正确生成CSV文件
引言 在大数据时代,爬虫技术成为获取和分析网络数据的重要工具。然而,许多开发者在使用Python编写爬虫时,常常遇到数据输出问题,尤其是在生成CSV文件时出错。本文将详细介绍如何解决这些问题,并提供使用代理IP和多线程…...

SCI一区TOP|徒步优化算法(HOA)原理及实现【免费获取Matlab代码】
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献5.代码获取 1.背景 2024年,SO Oladejo受到徒步旅行启发,提出了徒步优化算法(Hiking Optimization Algorithm, HOA)。 2.算法原理 2.1算法思想 HOA灵感来自于…...

Android的activity广播无法接收,提示process gone or crashing原因有可能是那些?
当Android的Activity无法接收广播,并且收到“process gone or crashing”的提示时,可能的原因有多种。以下是一些常见的原因和排查步骤: Activity生命周期问题: 如果Activity在广播发送之前就已经被销毁(例如…...

如何将等保2.0的要求融入日常安全运维实践中?
等保2.0的基本要求 等保2.0是中国网络安全领域的基本国策和基本制度,它要求网络运营商按照网络安全等级保护制度的要求,履行相关的安全保护义务。等保2.0的实施得到了《中华人民共和国网络安全法》等法律法规的支持,要求相关行业和单位必须按…...

51单片机嵌入式开发:STC89C52环境配置到点亮LED
STC89C52环境配置到点亮LED 1 环境配置1.1 硬件环境1.2 编译环境1.3 烧录环境 2 工程配置2.1 工程框架2.2 工程创建2.3 参数配置 3 点亮一个LED3.1 原理图解读3.2 代码配置3.3 演示 4 总结 1 环境配置 1.1 硬件环境 硬件环境采用“华晴电子”的MINIEL-89C开发板,这…...

源代码加密:保护你的数字宝藏
在当今日益复杂的网络安全环境中,源代码作为企业的核心知识产权,其安全保护显得尤为重要。传统的源代码加密方法虽能提供一定的保护,但在应对新型威胁和复杂场景时,往往显得力不从心。而SDC沙盒技术的出现,为源代码加密…...

Jackson库使用教程
1. Jackson概述 定义: Jackson是一个基于Java的开源JSON解析工具,用于Java对象与JSON数据的互相转换。示例JSON:{"author": "一路向北_Coding","age": 20,"hobbies": ["coding", "leetcode", "r…...

汉王、绘王签字版调用封装
说明 需要配合汉王或绘王签字版驱动以及对应的sdk服务使用 constants.js //汉王、绘王sdk websocket连接地址 export const WS_URLS {1:ws://127.0.0.1:29999, //汉王2:ws://127.0.0.1:7181, }export const COMMAND1 {1: {HWPenSign: "HWStartSign",nLogo: "…...

如何在TikTok上获得更多观看量:12个流量秘诀
TikTok作为热门海外社媒,在跨境出海行业中成为新兴的推广渠道,但你知道如何让你的TikTok赢得更多关注次数吗?如果您正在寻找增加 TikTok 观看次数的方法,接下来这12种策略,你需要一一做好! 1. 在内容中添加…...

vue模板语法v-html
模板语法v-html vue使用一种基于HTML的模板语法,使我们能够声明式的将其组件实例的数据绑定到呈现的DOM上,所有的vue模板都是语法层面的HTML,可以被符合规范的浏览器和HTML解释器解析。 一.文本插值 最基本的数据绑定形式是文本插值&#…...
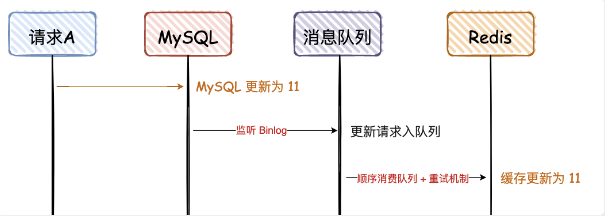
13 Redis-- 数据一致性模型、MySQL 和 Redis 的数据一致性
数据一致性模型 根据一致性的强弱分类,可以将一致性模型按以下顺序排列: 强一致性 > 最终一致性 > 弱一致性 数据一致性模型一般用于分布式系统中,目的是定义多个节点间的同步规范。 在这里,我们将其引入数据库和缓存组…...

启动Nuxt-hub-starter: Failed to initialize wrangler bindings proxy write EOF
重新安装 node.js 这样做可以确保下载到了适合的 Windows 框架、Chocolatey(一款Windows包管理工具)、Python 等资源。 这个错误与Node版本、pnpm/yarn 的版本无关! Node.js — Download Node.js (nodejs.org)...

技术驱动旅游创新!深度解析景区导览小程序的地图渲染与AR导航技术
随着现代生活节奏的加快,人们在外出旅游时更倾向于轻便出行,携带导览地图已成为过去。然而,面对景区广阔的面积和众多景点,游客常常感到迷茫,难以快速定位到自己所需的地点。景区导览小程序让游客只需搜索景区名称&…...

二叉树之遍历
二叉树之遍历 二叉树遍历遍历分类前序遍历流程描述代码实现 中序遍历流程描述代码实现 后序遍历流程描述代码实现 层次遍历流程描述代码实现 总结 二叉树遍历 遍历分类 遍历二叉树的思路有 4 种,分别是: 前序遍历二叉树,有递归和非递归两种…...
)
【经验贴】如何做好自己的职业规划(技术转项目经理)
我有几个问题想问大家 第一,你了解自己吗?你知道自己想要是什么吗?你了解自己的优势劣势吗? 第二,你了解这个行业吗?你知道这个行业是如何发展起来的吗?你了解这个行业的背景吗?你…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
