pyecharts可视化案例大全(1~10)
pyecharts可视化案例大全
- 一、堆叠柱状图
- 二、关闭坐标轴显示
- 三、自定义坐标轴标签文本
- 四、更改坐标轴数据类型
- 五、双Y轴【直方图&折线图】
- 六、直方图——双Y轴
- 七、折线图——双X轴
- 八、图例选择设置单选
- 九、缩略轴——inside组件
- 十、缩略轴——slider组件
一、堆叠柱状图
不同系列的数据使用相同的stack值会堆叠在一起 。
from pyecharts.charts import *
from pyecharts import options as opts
from pyecharts.faker import Fakerdef bar_stack():bar = Bar(init_opts=opts.InitOpts相关文章：
)
pyecharts可视化案例大全(1~10)
pyecharts可视化案例大全 一、堆叠柱状图二、关闭坐标轴显示三、自定义坐标轴标签文本四、更改坐标轴数据类型五、双Y轴【直方图&折线图】六、直方图——双Y轴七、折线图——双X轴八、图例选择设置单选九、缩略轴——inside组件十、缩略轴——slider组件一、堆叠柱状图 不…...
SpringBoot 启动流程一
SpringBoot启动流程一 我们首先创建一个新的springboot工程 我们不添加任何依赖 查看一下pom文件 我们创建一个文本文档 记录我们的工作流程 我们需要的是通过打断点实现 我们首先看一下启动响应类 package com.bigdata1421.start_up;import org.springframework.boot.Spr…...
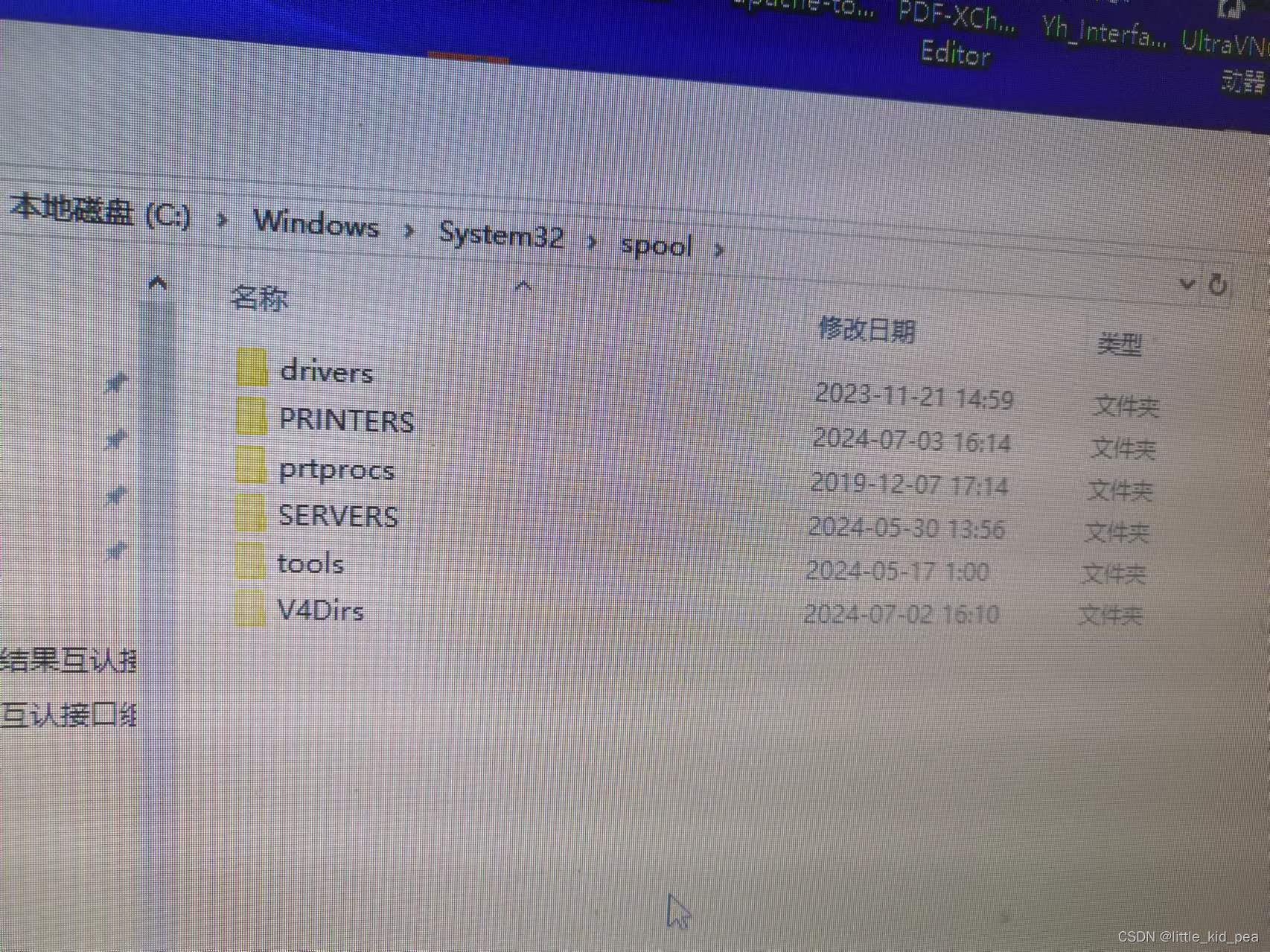
打印机删除副本以后无法安装打印机驱动
根据知乎文章解决打印机驱动副本存在多个，打印机驱动无法删除，或者驱动包无法删除等问题。的方法删除打印机副本以后发现无论如何也装不上驱动了。 要么驱动安装成功，但是设备仍然是指定状态。 后面发现是删错文件夹了，教程里让删…...
Vue3中为Ant Design Vue中Modal.confirm自定义内容
在一次业务开发时代码时，碰到了一种既想要Modal.confirm样式，又想要定制其content内容的情况。 大部分情况下，使用Modal.method()这种方式时，可能content内容固定都是字符串，那如果想要做更高级的交互怎么办ÿ…...
智能猫砂盆到底哪家好用？自费实测聚宠、糯雪、CEWEY真实反馈！
快到夏天了，是不是还有人因为没挑选到喜欢的智能猫砂盆而苦恼着？太便宜怕不好用，太贵怕质量比不上价格。来来去去拖到现在还没决定，我作为养了四年猫的资深铲屎官，今天就来给大家传授经验，关于我是怎么从好…...
初阶数据结构之二叉树
那么本篇文是初阶数据结构这个系列的最后一篇文章，那么闲话少叙，我们直接进入正题 在讲二叉树的一些之前知识点之前，我先给大家送个小礼物哈 手搓二叉树 typedef int BTDataType ; typedef struct BinaryTreeNode { BTDataType _data …...
代码随想三刷动态规划篇8
代码随想三刷动态规划篇8 122. 买卖股票的最佳时机 II题目代码 123. 买卖股票的最佳时机 III题目代码 188. 买卖股票的最佳时机 IV题目代码 309. 买卖股票的最佳时机含冷冻期题目代码 122. 买卖股票的最佳时机 II 题目 链接 代码 class Solution {public int maxProfit(int…...
服务拆分的原则
目录 一、单一职责原则 二、服务自治原则 三、单向依赖 一、单一职责原则 单⼀职责原则原本是面向对象设计中的⼀个基本原则, 它指的是⼀个类应该专注于单⼀功能. 不要存在多于⼀个导致类变更的原因 在微服务架构中, ⼀个微服务也应该只负责⼀个功能或业务领域, 每个服务应该…...
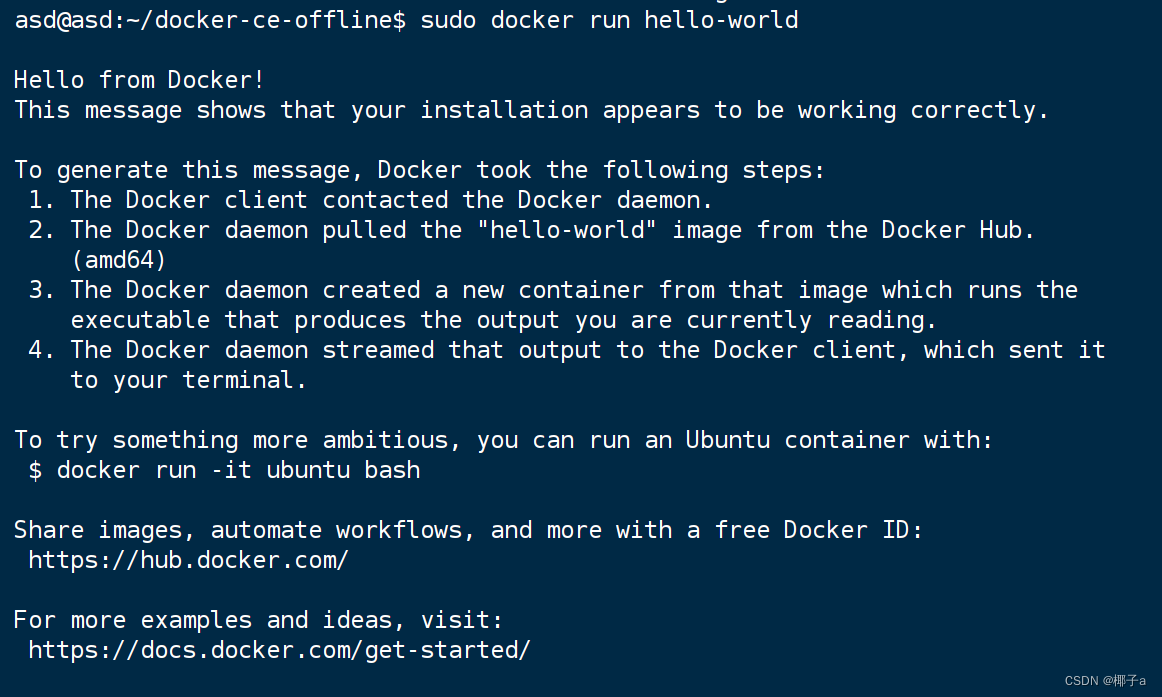
离线安装docker社区版
提示：以下所有命令都在Ubuntu-24.04-live-server-amd64系统中运行 文章目录 前言一、离线包制作二、在目标系统上离线安装Docker CE总结 前言 安全原因，内部机器不能联网，要给新机器安装 docker-ce 只能使用离线安装方法。如果使用本文的下载…...
徒手绘制 Android 通用进度条
拖动条（FlexSeekBar），在Android的各个地方都非常常用，本文旨在自研一套通用的进度条，非常适合车载App使用 样式如下： 使用示例 <!--默认用法--> <com.max.android.ui.seekbar.FlexSeekBarandroi…...
【TB作品】矩阵键盘电话拨号，ATMEGA16单片机，Proteus仿真 atmega16矩阵键盘电话拨号
atmega16矩阵键盘电话拨号 c代码和仿真图： 使用ATmega16实现矩阵键盘电话拨号功能 项目背景 在电子设计和嵌入式系统开发中，矩阵键盘是常见的人机交互方式。它可以实现较多按键的输入，同时节省单片机的I/O资源。结合LCD显示和蜂鸣器&am…...
JavaScript(6)——数据类型转换
为什么需要类型转换？ JavaScript是弱数据类型：JavaScript不知道变量到底属于哪种数据类型，只有赋值了才清除 使用表单，prompt获取的数据默认为字符串类型，此时不能直接进行算数运算 隐式转换 某些运算符被执行时&am…...
概率论与数理统计_下_科学出版社
contents 前言第5章 大数定律与中心极限定理独立同分布中心极限定理 第6章 数理统计的基本概念6.1 总体与样本6.2 经验分布与频率直方图6.3 统计量6.4 正态总体抽样分布定理6.4.1 卡方分布、t 分布、F 分布6.4.2 正态总体抽样分布基本定理 第7章 参数估计7.1 点估计7.1.1 矩估计…...
Android 复习layer-list使用
<shape android:shape"rectangle"> <size android:width"1dp" android:height"100px" /> <solid android:color"#FFFFFF" /> </shape> 通过shape画线段,通过 <item android:gravity"left|top"…...
汉光联创HGLM2200N黑白激光多功能一体机加粉及常见问题处理
基本参数： 机器型号：HGLM2200N 产品名称：A4黑白激光多功能一体机 基础功能：打印、扫描、复印 打印速度：22页/分钟 纸张输入容量：150-249页 单面支持纸张尺寸：A4、A5、A6 产品尺寸&#x…...
引领汽车软件开发走向ASPICE认证之路
亚远景科技与ASPICE认证的关系可以从以下几个方面来阐述： (要明确的是：在ASPICE行业中专业来说，ASPICE项目是没有认证，而只有评估。不过，为了方便沟通，人们常将这一评估过程称为认证。） 行业专…...
【C/C++ new/delete和malloc/free的异同及原理】
new/delete和malloc/free都是用于在C（以及C语言在malloc/free的情况下）中动态申请和释放内存的机制，但它们之间存在一些显著的异同点。以下是对这两组函数/运算符的异同点的详细分析： 相同点 目的相同：两者都用于在堆…...
Maven Archetype 自定义项目模板：高效开发的最佳实践
文章目录 前言一、Maven Archetype二、创建自定义 Maven Archetype三、定制 Archetype 模板四、手动创建 Archetype 模板项目五、FAQ5.1 如何删除自定义的模板5.2 是否可以在模板中使用空文件夹 六、小结推荐阅读 前言 在软件开发中，标准化和快速初始化项目结构能够…...
vue的ESLint 4格缩进 笔记
https://chatgpt.com/share/738c8560-5271-45c4-9de0-511fad862109 一，代码4格缩进设置 .eslintrc.js文件 module.exports { "rules": { "indent": ["error", 4] } }; 自动修复命令 npx eslint --fix "src/**/*.{…...
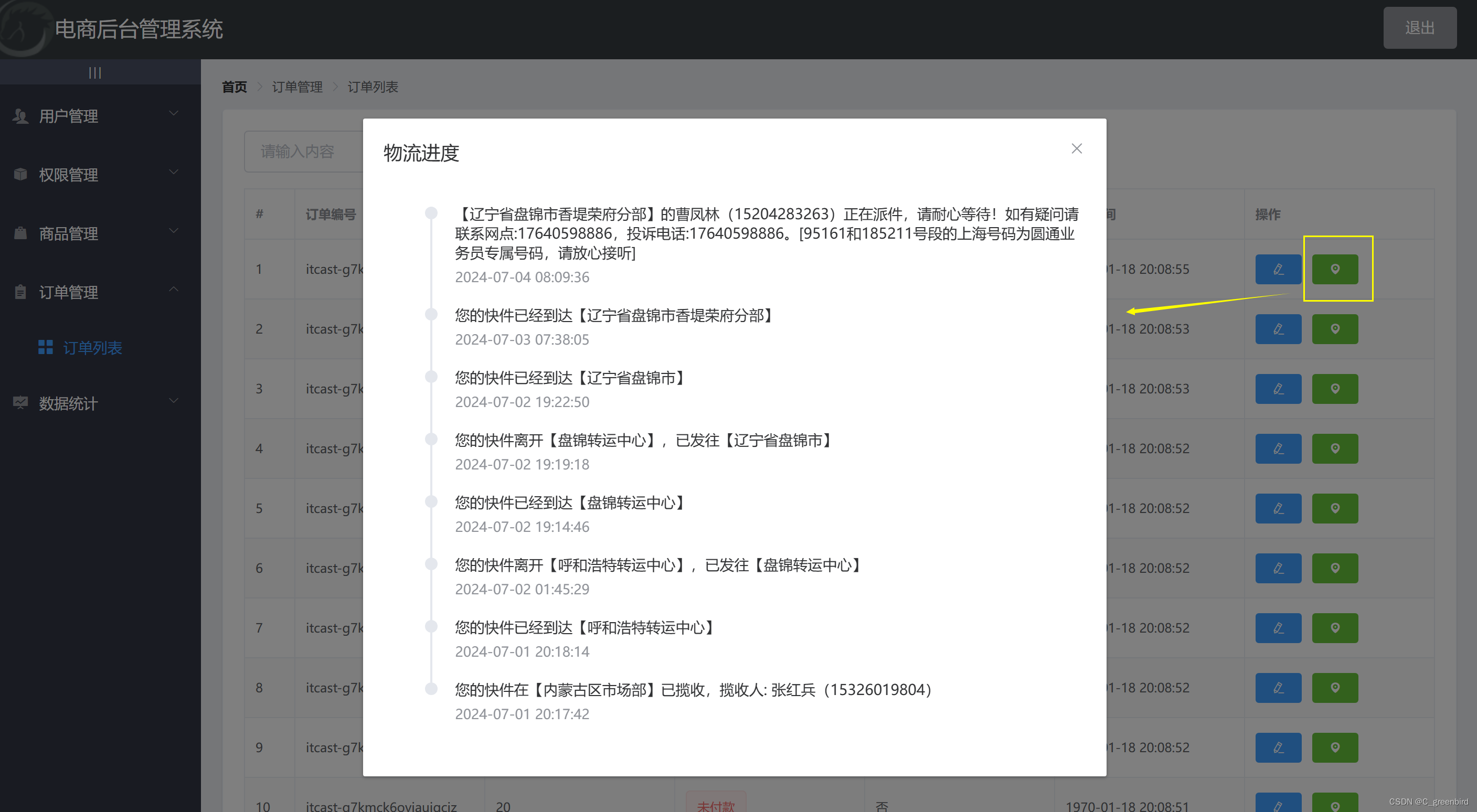
【前端项目笔记】8 订单管理
订单管理 效果展示： 在开发功能之前先创建分支order cls 清屏 git branch 查看所有分支（*代表当前分支） git checkout -b order 新建分支order git push -u origin order 将本地的当前分支提交到云端仓库origin中命名为order 通过路由方式…...
日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下，越来越多的求职者将目光投向了日本及中日双语岗位。但是，一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧？面对生疏的日语交流环境，即便提前恶补了…...
使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架，专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用，其中包含三个使用通用基本模板的页面。在此…...
golang循环变量捕获问题
在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景 看这个代码片段： fo…...
IGP（Interior Gateway Protocol，内部网关协议）
IGP（Interior Gateway Protocol，内部网关协议） 是一种用于在一个自治系统（AS）内部传递路由信息的路由协议，主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
什么是库存周转？如何用进销存系统提高库存周转率？
你可能听说过这样一句话： “利润不是赚出来的，是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业，很多企业看着销售不错，账上却没钱、利润也不见了，一翻库存才发现： 一堆卖不动的旧货…...
ffmpeg（四）：滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具，可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下： ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜： ffmpeg…...
Python爬虫（一）：爬虫伪装
一、网站防爬机制概述 在当今互联网环境中，具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类： 身份验证机制：直接将未经授权的爬虫阻挡在外反爬技术体系：通过各种技术手段增加爬虫获取数据的难度…...
C# SqlSugar：依赖注入与仓储模式实践
C# SqlSugar：依赖注入与仓储模式实践 在 C# 的应用开发中，数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护，许多开发者会选择成熟的 ORM（对象关系映射）框架，SqlSugar 就是其中备受…...
高防服务器能够抵御哪些网络攻击呢？
高防服务器作为一种有着高度防御能力的服务器，可以帮助网站应对分布式拒绝服务攻击，有效识别和清理一些恶意的网络流量，为用户提供安全且稳定的网络环境，那么，高防服务器一般都可以抵御哪些网络攻击呢？下面…...